Лекции - Машины Тьюринга. Основы теории вычислимости. Булевы функции и пропозициональные формулы
Подождите немного. Документ загружается.


•
•
•
M
x, y, z, n ∈ N, n > 2 x
n
+ y
n
= z
n
M

Γ
Γ = {x
1
, x
2
, x
3
, . . . }
•
•
A (A)
•
A ¬A
•
A, B A ∧ B
•
A, B A ∨ B
•
A, B A → B

•
x
1
•
x
1
∧ ¬x
1
•
x
1
∨ ¬x
1
•
(x
1
∨ x
2
) → x
3
•
(x
1
∨ ¬x
2
) ∧ (¬x
1
∨ x
3
) ∧ (x
3
∨ x
2
)
•
(x
1
∧ ¬x
2
) ∨ (¬x
1
∧ x
3
) ∨ (x
3
∧ x
2
)
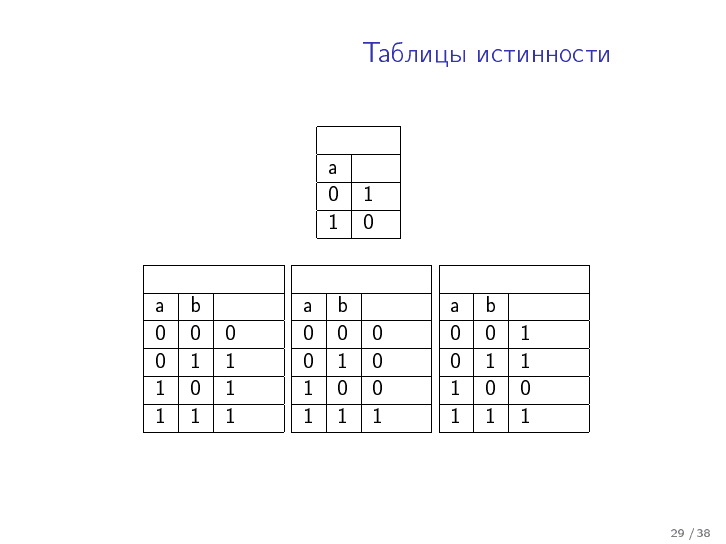
¬
¬a
∨
a ∨ b
∧
a ∧ b
→
a → b

ϕ
x
1
, x
2
, . . . , x
n
ϕ
σ : {x
1
, x
2
, . . . , x
n
} → {0, 1}
I
σ
(ϕ)
•
I
σ
(x
i
) = σ(x
i
)
•
I
σ
((A)) = I
σ
(A)
•
I
σ
(¬A) = ¬I
σ
(A)
•
I
σ
(A ∧ B) = I
σ
(A) ∧ I
σ
(B)
•
I
σ
(A ∨ B) = I
σ
(A) ∨ I
σ
(B)
•
I
σ
(A → B) = I
σ
(A) → I
σ
(B)

{0, 1}
n
{0, 1}
n
{0, 1}
n
{0, 1}
•
f (x
1
, x
2
, . . . , x
n
) = x
1
+ x
2
+ · · · + x
n
mod 2
•
f (x
1
, x
2
, . . . , x
n
) =
1, x
1
+ x
2
+ · · · + x
n
≥
n
2
0, x
1
+ x
2
+ · · · + x
n
<
n
2
•
f (x
1
, x
2
, . . . , x
n
) =
(
1, x
1
x
2
. . . x
n
−
0,

{0, 1}
n
{0, 1}
n
{0, 1}
n
{0, 1}
•
f (x
1
, x
2
, . . . , x
n
) = x
1
+ x
2
+ · · · + x
n
mod 2
•
f (x
1
, x
2
, . . . , x
n
) =
1, x
1
+ x
2
+ · · · + x
n
≥
n
2
0, x
1
+ x
2
+ · · · + x
n
<
n
2
•
f (x
1
, x
2
, . . . , x
n
) =
(
1, x
1
x
2
. . . x
n
−
0,

{0, 1}
n
{0, 1}
n
{0, 1}
n
{0, 1}
•
f (x
1
, x
2
, . . . , x
n
) = x
1
+ x
2
+ · · · + x
n
mod 2
•
f (x
1
, x
2
, . . . , x
n
) =
1, x
1
+ x
2
+ · · · + x
n
≥
n
2
0, x
1
+ x
2
+ · · · + x
n
<
n
2
•
f (x
1
, x
2
, . . . , x
n
) =
(
1, x
1
x
2
. . . x
n
−
0,

{0, 1}
n
{0, 1}
n
{0, 1}
n
{0, 1}
•
f (x
1
, x
2
, . . . , x
n
) = x
1
+ x
2
+ · · · + x
n
mod 2
•
f (x
1
, x
2
, . . . , x
n
) =
1, x
1
+ x
2
+ · · · + x
n
≥
n
2
0, x
1
+ x
2
+ · · · + x
n
<
n
2
•
f (x
1
, x
2
, . . . , x
n
) =
(
1, x
1
x
2
. . . x
n
−
0,

x
i
¬x
i
(x
1
∨ ¬x
2
∨ x
3
)
(x
1
∨ ¬x
2
∨ x
3
) ∧ (¬x
1
∨ ¬x
3
) ∧ ¬x
1
(x
1
∧ ¬x
2
∧ x
3
)
(x
1
∧ ¬x
2
∧ x
3
) ∨ (¬x
1
∧ ¬x
3
) ∨ ¬x
1
