Лекции - Физические основы сверпроводимости
Подождите немного. Документ загружается.


101
Для того, чтобы оценить величину этой силы, найдем величину тока, который нужно
пропустить через сверхпроводник, для того, чтобы преодолеть эту силу. Сила Лоренца,
действующая на единицу длины вихря, равна
0
JF
Приравнивая ее силе пиннинга (8.4), получим
0
2
0
2
c
H
J .
Учитывая, что
0
0
2
c
H , получаем:
22
c
H
J .
Возьмем в качестве примера характеристики типичного сверхпроводника 2-го рода NbTi,
5
103.1
c
H А.м,
300
нм, то получим плотность тока порядка
50
J
кА/мм
2
. Эта
величина по порядку величины совпадает с найденной ранее плотностью тока
распаривания, который является максимально возможной плотностью тока в
сверхпроводнике. Таким образом дефекты в сверхпроводниках могут удерживать вихри
настолько сильно, что для их срыва необходимо пропускать предельные токи.
8.4. Теория критического состояния Кима - Андерсона.
Электромагнитные свойства жестких сверхпроводников 2-го рода в значительной степени
определяются способностью центров пиннинга удерживать отдельные флюксоиды и
целые связки магнитного потока. Рассмотрим процесс проникновения внешнего
магнитного поля в сверхпроводящую пластину. До тех пор, пока максимальная
напряженность магнитного поля не превышает первого критического значения Н
с1
, оно
полностью выталкивается из объема сверхпроводника. Как только напряженность
магнитного поля превысит уровень Н
с1
, первые кванты магнитного потока устремятся
вглубь пластины. Однако из-за наличия большого количества центров пиннинга они будут
захвачены и остановлены в непосредственной близости от границы объекта. Поскольку в
приграничном слое магнитное поле меняется от некоторого максимального значения до
нуля, то автоматически возникают экранирующие токи, плотность которых подчиняется
уравнению Максвелла:
JHrot
(или
y
z
J
dx
dH
для пластины.)
При дальнейшем увеличении магнитного поля могут создаться условия для срыва
флюксоидов с центров пиннинга и их дальнейшего продвижения вглубь пластины. Это
102
произойдет, как только электромагнитная сила, действующая на магнитные вихри,
превысит силу, удерживающую их на центрах пиннинга. Плотность тока, при которой
происходит срыв флюксоидов, равна критической. Отсюда следует, что любое изменение
распределений магнитного поля и плотности тока происходит только при равенстве
плотности тока критическому значению, а, следовательно, плотность тока в жестких
сверхпроводниках 2-го рода может принимать только три значения – 0 и ±J
c
.
Если усредненную объемную плотность сил пиннинга обозначить F
p
, то уравнение
равновесия, при котором отсутствует течение магнитного потока, и при котором,
соответственно, сопротивление у сверхпроводника отсутствует, будет иметь вид:
pc
FBJ
Это уравнение носит название уравнения критического состояния для жестких
сверхпроводников 2-го рода. Как видно, оно устанавливает связь между величиной
магнитного поля и критическим током. Следует, однако, иметь в виду, что величина
объемной силы пиннинга F
p
в свою очередь может зависеть от уровня магнитного поля.
8.4.1 Модель критического состояния Бина – Лондона
Существуют различные физические модели, которые описывают эту зависимость.
Наиболее простой из них является модель Бина – Лондона. В ее рамках предполагается,
что объемная сила пиннинга пропорциональна индукции магнитного поля.
BJF
p
0
В этих условиях критический ток оказывается постоянным, не зависящим от величины
магнитного поля.
0
JJ
c
Конечно, это является существенным упрощением реальной картины. Тем не менее, эта
модель очень часто используется на практике. Это объясняется следующими
обстоятельствами. Во-первых модель Бина – Лондона относительно проста и зачастую
позволяет получить адекватное описание процессов, происходящих в жестких
сверхпроводниках 2-го рода, без привлечение сложного и громоздкого аппарата
вычислительной математики. Во-вторых для многих, хотя и не для всех, жестких
сверхпроводников зависимость критического тока от индукции магнитного поля
действительно может считаться приближенно постоянной (рис.8.5). Как видно из
приведенных на этом рисунке зависимостей, в области маленьких магнитных полей
критический ток уменьшается с увеличением магнитного поля. Это довольно
естественное поведение критического тока объясняется тем, что для поддержание
высокого тока необходимо присутствие большого числа сильных центров пиннинга. А в
соответствии с законами статистики, количество таких центров уменьшается с
увеличением их способности притягивать вихри. Однако при достижении магнитного
поля, сравнимого со вторым критическим, скорость снижения критической плотности
тока замедляется, а в некоторых случаях даже наблюдается ее рост. Это явление получило
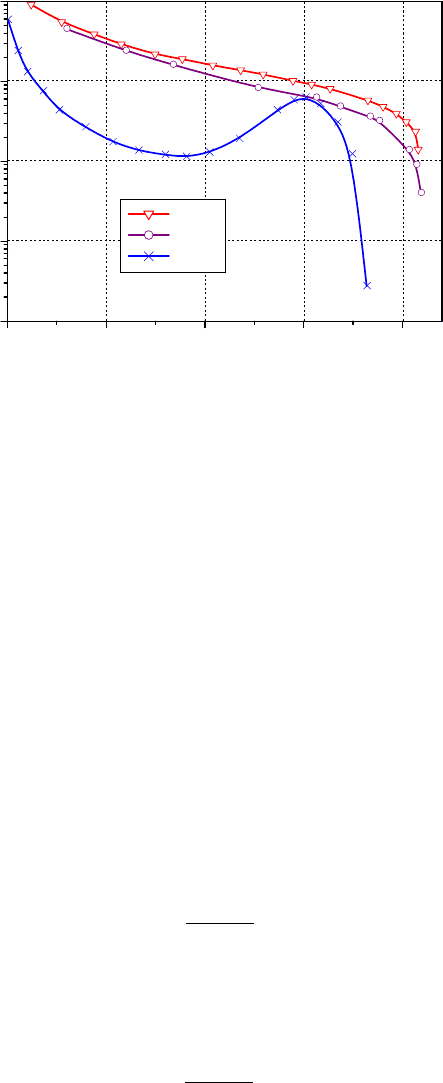
103
название пик-эффекта. Объясняется оно тем, что при высоких уровнях магнитного поля
вихри объединяются в единую жесткую треугольную решетку. В этих условиях
немногочисленные сильные центры пиннинга способны удержать большое количество
вихрей даже в том случае, если в его окрестности оказался только один флюксоид.
0 5 10 15 20
0,01
0,1
1
10
100
Критический ток, А
Индукция магнитного поля, T
V
3
Si
Nb
3
Sn
V
3
Ga
Рис. 8.5. Критические токи некоторых жестких сверхпроводников. Из приведенных
данных видно, что при индукциях в диапазоне В =1
10 Т сила пиннинга для них
действительно может считаться приблизительно постоянной. Данные приведены для
цилиндрических образцов диаметром 0.5 мм.
Типичные значения плотности критического тока в модели Бина – Лондона обычно
находятся вблизи уровня
3
0
10~J А/мм
2
и иногда существенно зависят от типа
используемого сверхпроводника.
8.4.2. Модель критического состояния Кима.
Еще одна модель критического состояния сверхпроводников 2-го рода носит название
модели критического состояния Кима. В ней связь между объемной силой пиннинга и
индукцией магнитного поля представляется в виде более сложной зависимости:
0
BB
B
F
p
где
и
0
B - эмпирические коэффициенты. Соответственно критический ток в этой
модели зависит от индукции магнитного поля:
0
BB
J
c

104
и при типичных значениях параметра
20 c
BB практически обратно пропорционален
индукции магнитного поля во всем диапазоне изменения магнитных полей за
исключением малых полей
0
BB или
0
BB . Очевидно, что Модель Кима не описывает
свойства сверхпроводников, в которых наблюдается пик-эффект. Тем не менее, она,
наряду с моделью Бина – Лондона, также используется в практических расчетах и, как
правило, позволяет получить точнее характеризовать свойства сверхпроводников.
Типичные значения параметров модели Кима можно оценить на примере одного из
наиболее часто используемых в технике жестких сверхпроводников – Nb
3
Sn. Для этого
материала были получены такие данные:
3
104.1
А/мм
2
∙Т,
06.0
0
B Т.
Понятно, что в диапазоне магнитных полей порядка
101
Т, где обычно применяются
сверхпроводники, параметром модели
0
B можно пренебречь, и практически модель Кима
задает обратно-пропорциональную зависимость между критическим током и индукцией
магнитного поля.
B
J
c
.
