Лекции - Дезактивация оборудования АЭС
Подождите немного. Документ загружается.

21
Дезактивация металлических радиоактивных отходов
Дезактивация с использованием озона
Комбинированная дезактивация паром и жидкой углекислотой
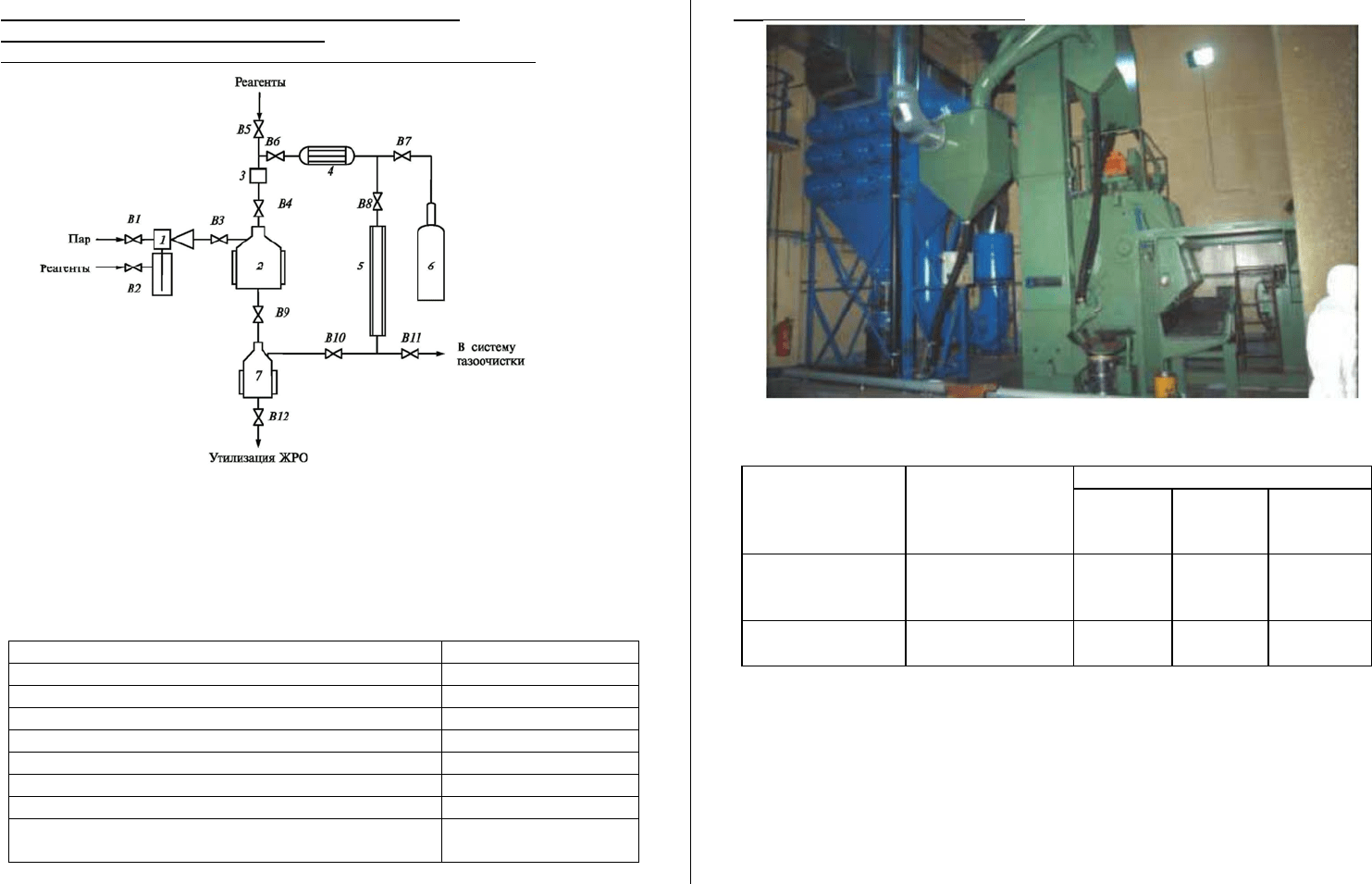
Рисунок 5.25 – 1. Схема установки паровой дезактивации и в среде жидкого
диоксида углерода: 1 — барботер с соплом; 2 — реактор; 3 — емкость-
смеситель; 4 — конденсатор; 5 — теплообменник; 6 — баллон с СО
2
; 7 — ис-
паритель; В1—В12 — вентили
Таблица 5.5 Технические характеристики установки комбинированного ме-
тода дезактивации с использованием паровой дезактивации и дезактивации в
среде сжиженного диоксида углерода
Рабочее давление пара 0,1 0,4 МПа
Максимальное давление пара 1,5 МПа
Рабочее давление диоксида углерода 7,0 МПа
Максимальное давление диоксида углерода 10,0 МПа
Максимальная скорость нагревания образца паром 15 °С/мин
Максимальная скорость охлаждения образца 35 °С/мин
Рабочая температура при обработке паром 120 130
о
С
Минимальная температура при конденсации 8 °С
Рабочая температура при обработке диоксидом уг-
лерода
15
–50 °С
Абразивные методы дезактивации
Рисунок 5.26 – Установка для абразивной дезактивации
Таблица 5.6 Эффективность гидроабразивной обработки в зависимости от
давления
После дезактивации
Поверхность
До дезактивации
р=180
бар, V=700
л/ч
р=120
бар, V=500
л/ч
р=70 бар
V=300 л/ч
Мощность дозы
γ-излучения, мкР
/ч
120 40 45 45
Активность,
β-частиц / см
2
*мин
500-15000 100 120 150
22
Венттруба
Вентсистема
здания
Предвари-
тельная
очистка
Сепаратор
Очистка
абразива
Радиоактивные
отходы
Регенерирован-
ный абразив
Абразив-
ный
бластер
Пыль
Отработанный
абразив
Воздух
Воздух
Воздух
Свежий
абразив
Продезак-
тивированный
металл
Загрязненный
металл
Слабозагрязненный
абразив без пыли
Грязный абразив
ипыль
(2,2 %)
(97,5 %)
(9,3 %)
Грязный
абразив
ипыль
Воздух
ипыль
Венттруба
Вентсистема
здания
Предвари-
тельная
очистка
Сепаратор
Очистка
абразива
Радиоактивные
отходы
Регенерирован-
ный абразив
Абразив-
ный
бластер
Пыль
Отработанный
абразив
Воздух
Воздух
Воздух
Свежий
абразив
Продезак-
тивированный
металл
Загрязненный
металл
Слабозагрязненный
абразив без пыли
Грязный абразив
ипыль
(2,2 %)
(97,5 %)
(9,3 %)
Грязный
абразив
ипыль
Воздух
ипыль
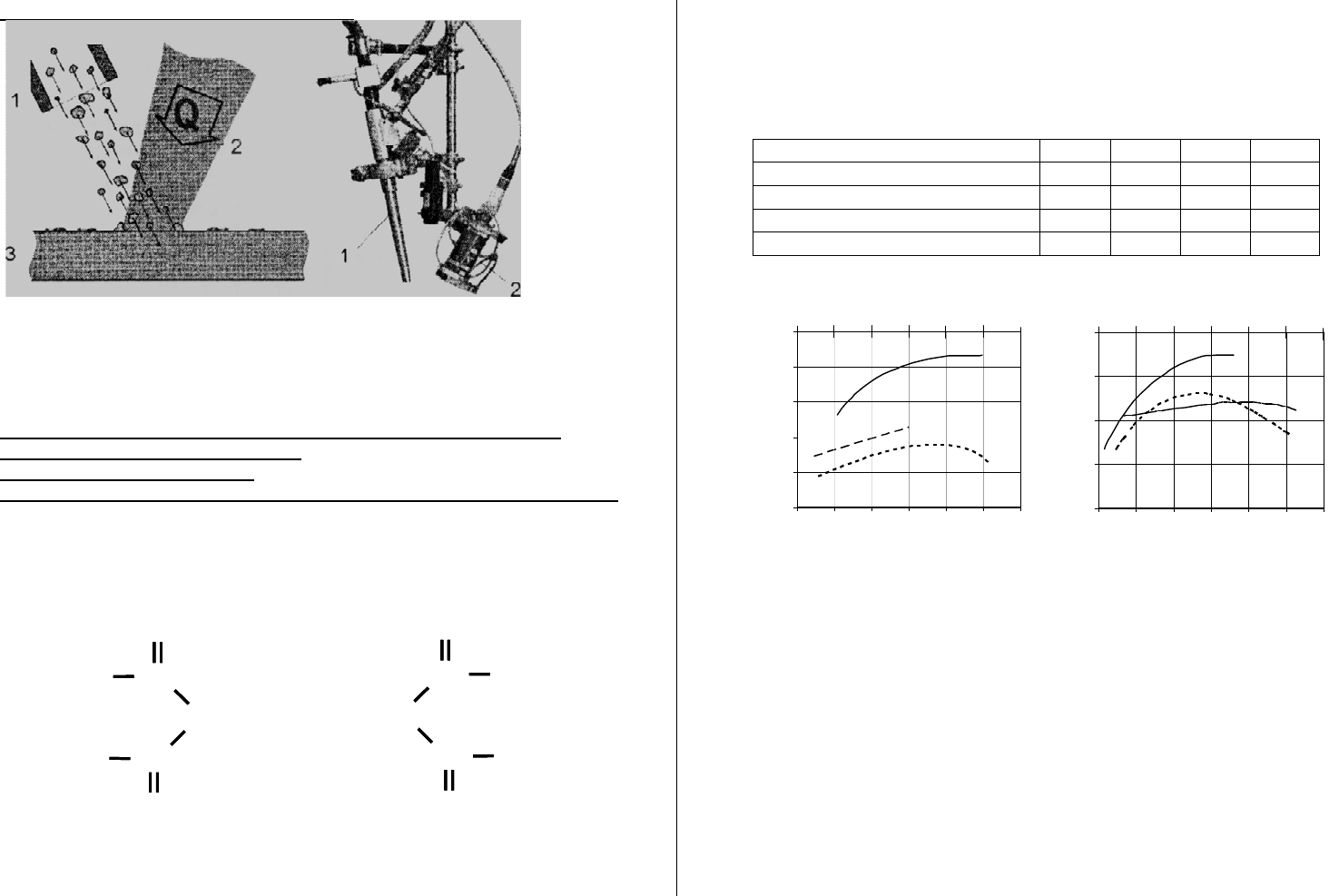
Рисунок 5.27 – Схема установки для абразивной дезактивации [221]
аэрогидродинамический метод.
Рисунок 5.28 – Схема работы АГД форсунки
Таблица 5.7 Технические характеристики установки MULTIBLUST
Давление сжатого воздуха (мПа) 0.4 – 1.2
Расход сжатого воздуха (м³/мин) 4--8
Расход рабочей жидкости (л/час) 40
Температура сжатого воздуха (мин.) С° 5
Расход промывочной жидкости/гидрофобизатора (л/час) 35
Производительность, м
2
/ч старая ржавчина 3
свежая 15
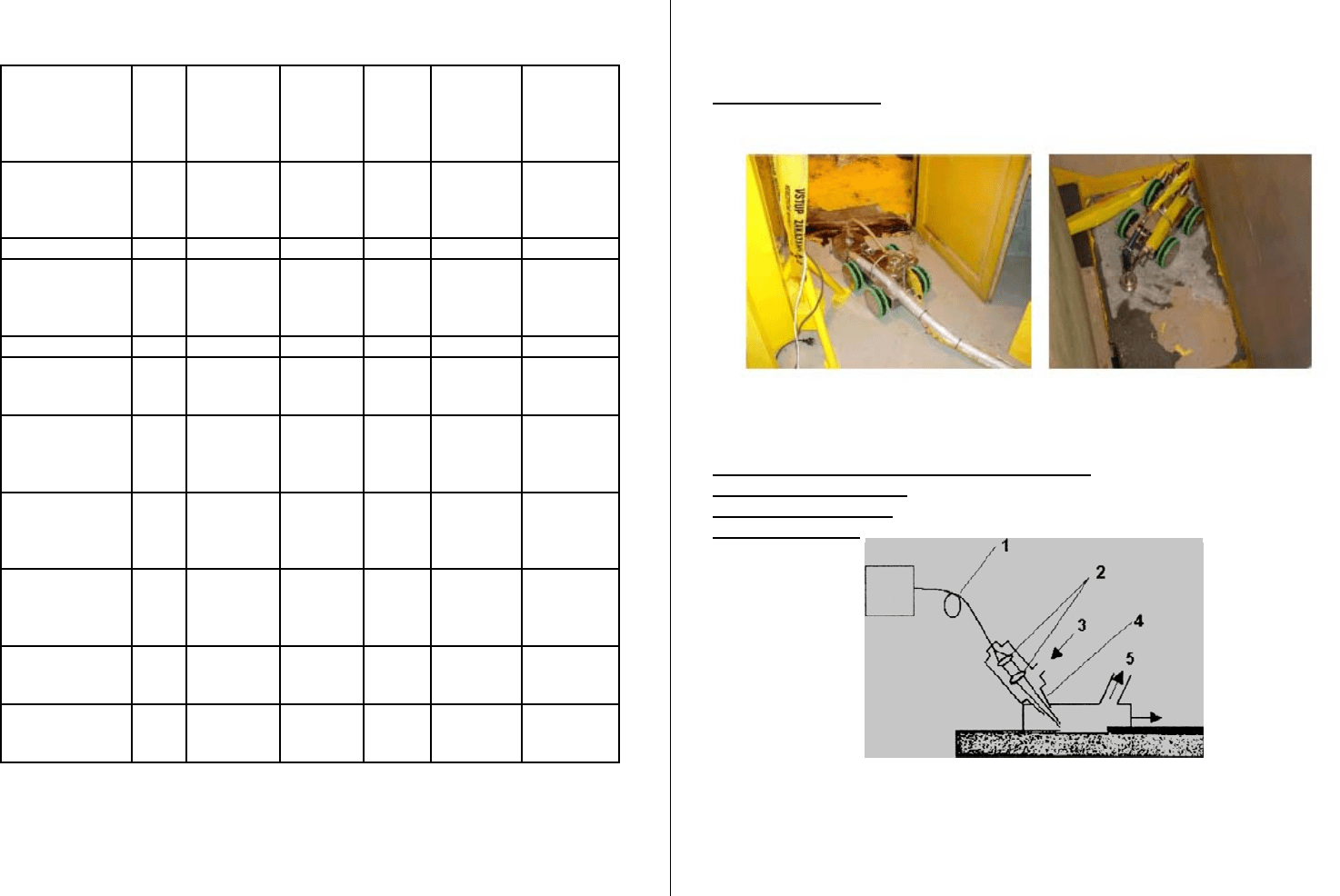
Рисунок 5.29 – Установка для осуществления АГД метода]
Рисунок 5.30 – Схема установки для осуществления АГД метода
23
5.4 Дезактивация АЭС при выводе из эксплуатации
5.4.1 Проблемы вывода из эксплуатации АЭС
Таблица 5.8 Характеристики действующих российских АЭС
АЭС
№
блока
Тип
реактора
Мощн.,
МВт, (эл.)
Год
ввода
в экс-
плуа-
тацию
Срок
окончания
эксплуата-
ции
Поколение
реактора
Балаковская
1
2
3
4
ВВЭР-1000
1000
1000
1000
1000
1985
1987
1988
1993
2015
2017
2018
2023
2
2
2
2
Белоярская 3 БН-600 600 1980 2010* 2
Билибинская
1
2
3
4
ЭГП-6
12
12
12
12
1974
1974
1975
1976
2009**
2009**
2010**
2011**
1
1
1
1
Волгодонская 1 ВВЭР-1000 1000 2002 2032 2
Калининская
1
2
3
ВВЭР-1000
1000
1000
1000
1984
1986
2005
2014
2016
2035
2
2
2
Кольская
1
2
3
4
ВВЭР-440
440
440
440
440
1973
1974
1979
1981
2008**
2009**
2009*
2011
1
1
2
2
Курская
1
2
3
4
РБМК-
1000
1000
1000
1000
1000
1976
1979
1983
1985
2011**
2009*
2013
2015
1
1
2
2
Ленинградская
1
2
3
4
РБМК-
1000
1000
1000
1000
1000
1973
1975
1979
1981
2008**
2010**
2009*
2011
1
1
2
2
Ново-
воронежская
3
4
5
ВВЭР-440
ВВЭР-440
ВВЭР-1000
417
417
1000
1971
1972
1980
2016
2017
2010*
1
1
2
Смоленская
1
2
3
РБМК-
1000
1000
1000
1000
1982
1985
1990
2012
2015
2020
2
2
2
* Планируется продление сроков эксплуатации энергоблоков с реакторами РБМК-
1000, ВВЭР-440 1-го поколения, БН-600 на 15 лет и с реакторами ВВЭР-440 и ВВЭР-1000 2-
го поколения на 20 лет;
** Обосновано продление срока эксплуатации на 15 лет и получена лицензия сро-
ком на 5 лет.
5.4.2 Концепция вывода из эксплуатации и дезактивации блоков с
РБМК
5.4.3 Зарубежный опыт дезактивации при выводе АЭС из эксплуата-
ции
Химические методы
LOMI, CORD, AP-CITROX и многие другие.
Рисунок 5.31 – Дистанционно управляемая установка для дезактивации пола
DOV-Deco
Гидроджеттинг под сверхвысоким давлением
Снятие слоя материала
Обдувка сухим льдом
Лазерные методы
Рисунок 5.32– Схема процесса удаления оксидного слоя с поверхности метал-
ла с использованием Nd-ИАГ-лазера: 1 − оптический волновод; 2 − линзы; 3 −
газ; 4 − газовое сопло; 5 − удаление загрязнений
Удаляемые частицы улавливаются на высокоэффективных воздушных фильтрах
(95%). Коэффициент очистки достигает 257.
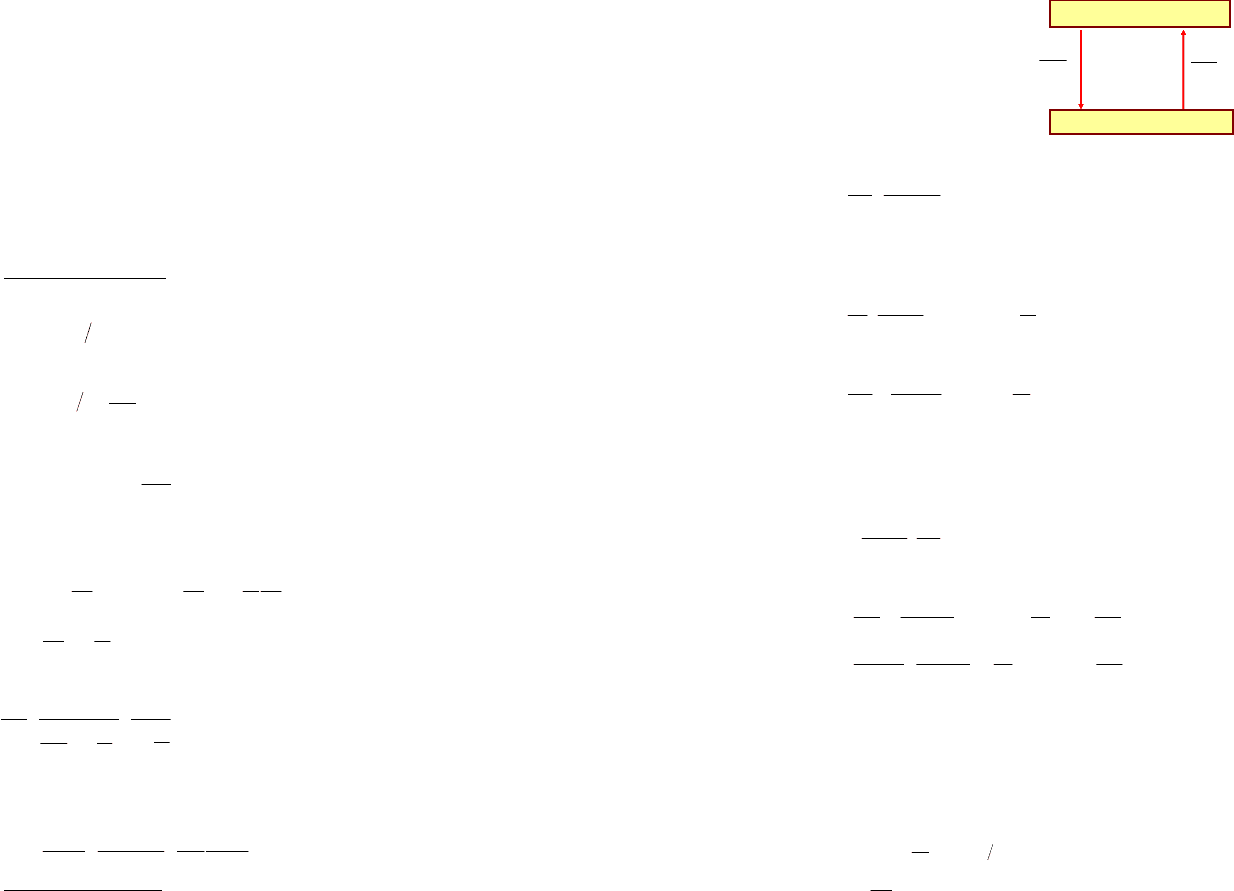
123
5.5 Особенности дезактивации полов производственных помещений и других го-
ризонтальных поверхностей большой площади
Рассмотрим процесс дезактивации горизонтальной поверхности пола, заключающийся в на-
несении на поверхность моющего раствора, протирки поверхности гигроскопичным материалом с
отжимом его в емкость с моющим раствором.
Принимаем следующие допущение:
1. Сорбция радионуклидов в гигроскопичном материале не учитывается, так же как и расход
раствора на его смачивание.
2. Загрязнение пола является равномерным и постоянным.
А
А
А
А
)N(
исх
)i(
исх
)2(
исх
)1(
исх
...... =
==
==
==
==
==
==
==
==
==
=
(5.11)
3. При нанесении загрязненного раствора на поверхность вторичной сорбции радионуклидов
не происходит.
4. Введем обозначения
К
д
– максимально возможный (предельный) при данном способе коэффициент дезактивации;
А
исх
– исходная активность поверхности, Ки/м
2
;
А
ост
– остаточная активность поверхности, Ки/м
2
;
δ
δδ
δ
– количество дезактивирующего раствора, нанесенного на поверхность, л/м
2
.
ε
εε
ε
– количество дезактивирующего раствора, остающегося на поверхности, л/м
2
;
V
0
– исходный объем емкости с дезактивирующим раствором, л.
N
– число участков, на которых происходит единичный акт дезактивации.
Рассмотрим последовательную дезактивацию нескольких участков площадью S=1 м
2
.
Дезактивация 1 участка.
Нанесено
δ
δδ
δ
литров чистого раствора. В раствор переходит количество активности, опреде-
ляемое предельным коэффициентом дезактивации:
КA
Q
Д
)1(
исх
)1(
пов
=
==
=
∆
∆∆
∆
(5.12)
Удельная активность радиоактивного вещества в дезактивирующем растворе на поверхности
пола
К
A
Q
С
Д
)1(
исх
)1(
пов
)1(
пов
δ
δδ
δ
δ
δδ
δ
=
==
==
==
=
∆
∆∆
∆
(5.13)
После сбора радиоактивного вещества с поверхности в емкость поступает количество актив-
ности, равное
(
((
( )
))
) (
((
(
)
))
)
ε
εε
εδ
δδ
δ
δ
δδ
δ
ε
εε
εδ
δδ
δ
−
−−
−−
−−
−
∆
∆∆
∆
=
==
==
==
=
К
A
С
Q
Д
)1(
исх
)1(
пов
)1(
пов
(5.14)
Оставшаяся на поверхности активность складывается из активности, обусловленной предель-
ным
К
Д
и активности, оставшейся с раствором (
ε
εε
ε
):
+
++
+=
==
=
=
==
=+
++
+=
==
=+
++
+=
==
=
δ
δδ
δ
ε
εε
ε
δ
δδ
δ
ε
εε
ε
ε
εε
ε
1
К
1
А
К
1
A
К
1
А
С
К
1
АА
Д
)1(
исх
Д
)1(
исх
Д
)1(
исх
)1(
пов
Д
)1(
исх
)1(
пов
(5.15)
Отсюда эффективный или фактический коэффициент дезактивации составит:
δ
δδ
δ
ε
εε
ε
δ
δδ
δ
ε
εε
ε
+
++
+
=
==
=
+
++
+
=
==
==
==
=
1
К
1
К
1
1
А
А
Кд
Д
Д
)1(
пов
)1(
исх
)1(
эфф
(5.16)
Если раствора на поверхности не остается (при идеальном собирании раствора), то эффектив-
ный КД будет равен элементарному или предельному КД.
Удельная активность в емкости после дезактивации 1-го участка составляет:
(
((
(
)
))
)
ε
εε
ε
ε
εε
εδ
δδ
δ
δ
δδ
δε
εε
ε
ε
εε
εδ
δδ
δ
ε
εε
ε
−
−−
−
=
==
=
−
−−
−
=
==
=
−
−−
−
=
==
=
−
−−
−−
−−
−
∆
∆∆
∆
VК
A
V
С
V
Q
С
0Д
)1(
исх
0
)1(
пов
0
)1(
пов
)1(
емк
(5.17)
Дезактивация 2 участка
124
После нанесения на очищаемую поверхность дезактивирующего раствора, уже содержащего
активность, в него дополнительно переходит активность, определяемая уравнением (5.3). Математи-
ческое описание получается достаточно громоздким, но ясно одно – коэффициент дезактивации ока-
жется меньше, чем на первом участке.
Поэтому представим процесс дезактивации как непрерывный, в которой емкость с дезакти-
вирующим раствором и поверхность обмениваются активностью (см. рис. 5.9).
Введем дополнительно понятие скорости дезактивации поверхности (м
2
/с) и обозначим ее
α
αα
α
.
Q
Емкость V=V
0
-εα
εαεα
εαt
А
0
Поверхность
dt
dq
1
dt
dq
2
Q
Емкость V=V
0
-εα
εαεα
εαt
А
0
Поверхность
dt
dq
1
dt
dq
2
Рисунок 5.9 – Схема потоков активности при дезактивации пола.
Поступление радионуклидов на поверхность определяется уровнем активности в емкости:
δα
δαδα
δα
εα
εαεα
εα
tV
Q
dt
dq
0
1
−
−−
−
=
==
=
(5.18)
Очевидно, что в начальный момент времени раствор чистый и поступление активности на по-
верхность равно нулю.
Поступление в емкость определяется количеством собираемого раствора и количеством пе-
решедшей в него активности
(
((
( )
))
)
α
αα
α
α
αα
α
ε
εε
εδ
δδ
δ
εα
εαεα
εα
−
−−
−+
++
+
−
−−
−
=
==
=
−
−−
−
К
1
1А
tV
Q
dt
dq
Д
0
0
2
(5.19)
На основании этих двух уравнений можно написать уравнения для изменения активности на
поверхности и в емкости:
α
αα
αεα
εαεα
εα
εα
εαεα
εα
−
−−
−+
++
+
−
−−
−
−
−−
−=
==
=
К
1
1А
tV
Q
dt
dQ
Д
0
0
(5.20)
Уравнение для поверхности можно получить из условия сохранения материального баланса.
Поскольку
α
αα
αt
по сути, является продезактивированной площадью, то в любой момент времени спра-
ведливо:
Aα
αα
αt + Q = A
0
α
αα
αt
(5.21)
Продифференцировав уравнение (5.12) получим:
(
((
(
)
))
)
A
dt
dQ
dt
t*Ad
0
α
αα
αα
αα
α
=
==
=+
++
+
(5.22)
Заменяя dQ/dt на выражение (5.11) получим систему уравнений, однозначно определяющую
массоперенос в процессе дезактивации горизонтальных поверхностей:
(
((
( )
))
)
+
++
+
−
−−
−
=
==
=
−
−−
−+
++
+
−
−−
−
−
−−
−=
==
=
см
Ки
К
А
tV
Q
dt
t*Ad
с
Ки
К
1
1А
tV
Q
dt
dQ
2
Д
0
0
Д
0
0
ε
εε
ε
εα
εαεα
εα
α
αα
αεα
εαεα
εα
εα
εαεα
εα
(5.23)
В начальный момент времени активность в емкости равна нулю, а активность на поверхности
А
0
. В ходе дезактивации все большая активность переходит в раствор и все большая активность оста-
ется на поверхности. В какой-то момент времени активность на поверхности станет равна исходной.
Дальнейшая дезактивация приведет только к загрязнению поверхности, т.е.
А
превысит
А
0
. В емко-
сти активность нарастает по мере проведения дезактивации и достигает максимума, после чего коли-
чество активности в емкости начнет уменьшаться за счет уменьшения объема раствора. В конечном
итоге в емкости не останется раствора и активность в емкости станет равна нулю.
Введем две замены:
[
[[
[
]
]]
]
[
[[
[ ]
]]
]
с
V
сКи
К
1
1А
0
Д
0
εα
εαεα
εα
γ
γγ
γ
α
αα
α
β
ββ
β
=
==
=
−
−−
−=
==
=
(5.24)
125
Тогда первое уравнение системы можно записать в виде (
0≤t≤γ
γγ
γ
):
β
ββ
β
γ
γγ
γ
=
==
=
−
−−
−
+
++
+
t
Q
dt
dQ
(5.25)
Решая соответствующее однородное уравнение (правая часть 0), получим
=
==
=
+
++
+=
==
=
=
==
=
−
−−
−
−
−−
−
−
−−
−
t
C
Q
C
)t(Ln
LnQ
t
dt
Q
dQ
0
0
0
0
γ
γγ
γ
γ
γγ
γ
γ
γγ
γ
(5.27)
Решаем общее уравнение, которое представляем в виде:
β
ββ
β
γ
γγ
γ
γ
γγ
γ
=
==
=
−
−−
−
−
−−
−
Q
t
1
dt
d
t
(5.28)
Решение этого дифференциального уравнения может быть легко найдено:
(
((
( )
))
)
−
−−
−
−
−−
−
−
−−
−
−
−−
−
−
−−
−
−
−−
−
−
−−
−
∫
∫∫
∫
−
−−
−
−
−−
−
−
−−
−
−
−−
−
=
==
=
=
==
=
+
++
+
−
−−
−=
==
=
=
==
=
=
==
=
γ
γγ
γ
γ
γγ
γβ
ββ
β
γ
γγ
γ
γ
γγ
γ
γ
γγ
γβ
ββ
β
γ
γγ
γγ
γγ
γβ
ββ
β
γ
γγ
γ
γ
γγ
γβ
ββ
β
γ
γγ
γ
β
ββ
β
γ
γγ
γ
β
ββ
β
γ
γγ
γ
γ
γγ
γ
/t1
1
ln
t
t
ln
t
)ln(t
t
ln
t
dx
x
t
Q
Q
t
1
dt
d
t
t
0
(5.29)
При
t=γ
γγ
γ
весь раствор из емкости окажется на полу и активность в емкости будет равна нулю.
Существует момент времени, когда производная
dQ/dt
меняет знак, т.е. в этот момент она
равна нулю. Из (5.25) следует, что на этот момент времени
τ
ττ
τ
можно записать:
−
−−
−=
==
=
t
)(Q
γ
γγ
γβ
ββ
β
τ
ττ
τ
(5.30)
Подставляя решение (5.29) в (5.30) получим
(
((
( )
))
)
γ
γγ
γγ
γγ
γ
γ
γγ
γ
γ
γγ
γ
γ
γγ
γβ
ββ
β
γ
γγ
γ
γ
γγ
γβ
ββ
β
6321,0
e
1e
t
e
1
/t1
1
/t1
ln
t
/t1
1
ln
t
=
==
==
==
=
=
==
=
=
==
=−
−−
−
−
−−
−=
==
=
−
−−
−
−
−−
−
−
−−
−
−
−−
−
−
−−
−
(5.31)
Таким образом, площадь, которая может быть продезактивирована, определяется объемом
емкости и потерями раствора на поверхности:
ε
εε
ε
α
αα
α
V
6321,0
tS
0
äåçäåç
=
==
==
==
=
(5.22)
Остаточное загрязнение поверхности определяем из (5.22) и (5.29):
(
((
(
)
))
)
t
ln
t
t
A
)t(A
0
−
−−
−
−
−−
−
−
−−
−=
==
=
γ
γγ
γ
γ
γγ
γ
γ
γγ
γ
α
αα
α
β
ββ
β
(5.23)
Если уравнение (5.23) привести к виду:
t
t
ln
A
)t(A
t
0
−
−−
−
−
−−
−
−
−−
−=
==
=
γ
γγ
γ
γ
γγ
γ
α
αα
α
β
ββ
β
γ
γγ
γ
(5.24)
то можно показать, что в момент t=0
K
A
K
1
1AA
0
0
A
)t(A
Д
0
Д
000
=
==
=
−
−−
−−
−−
−=
==
=
⋅
⋅⋅
⋅−
−−
−=
==
=
α
αα
α
β
ββ
β
(5.25)
126
Это соответствует физическому смыслу величины остаточного загрязнения.
При
t=γ
γγ
γ
соответственно
A(t)=A
0
.
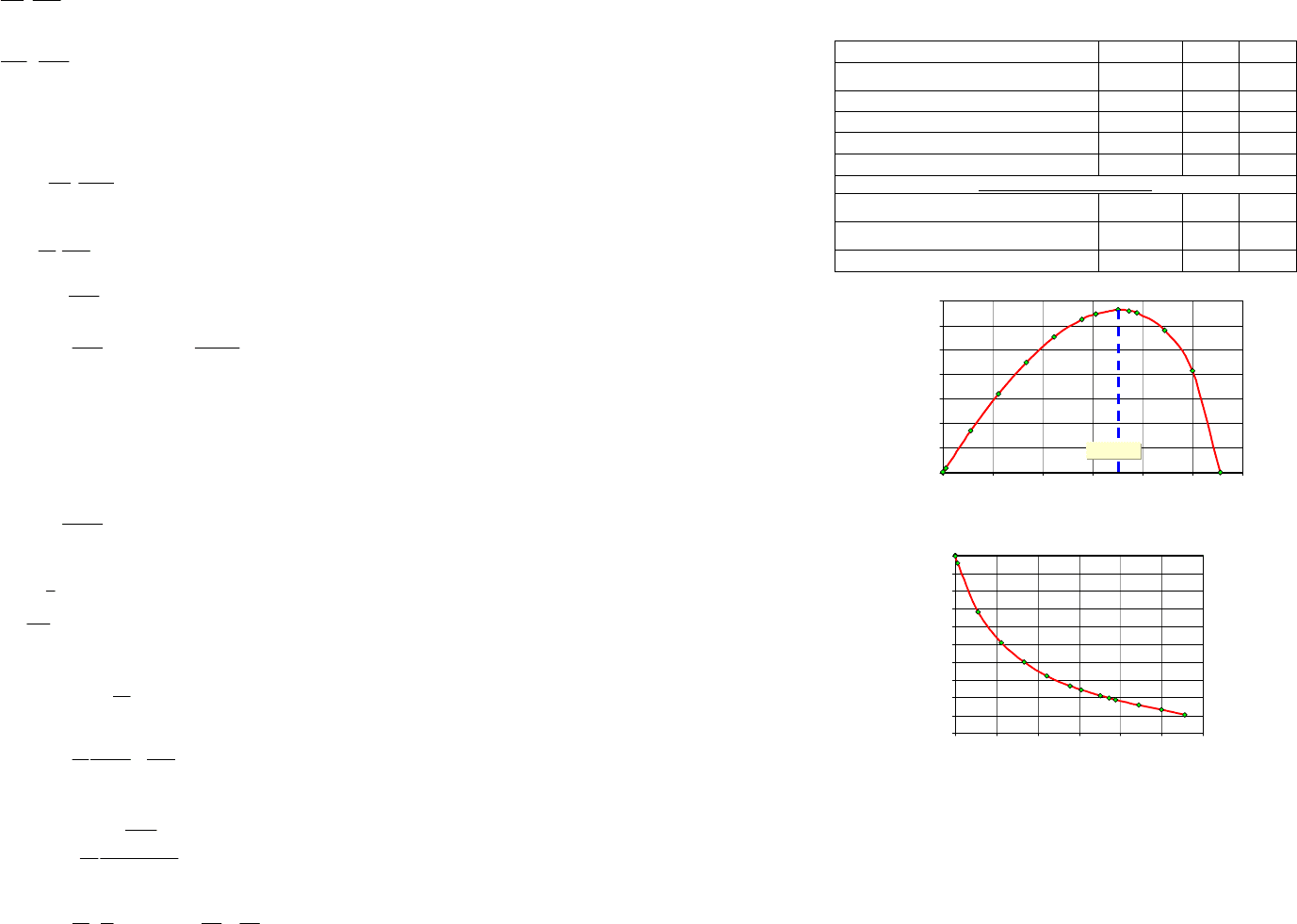
На рис. 5.35 и 5.36 показано изменение активности в емкости м эффективного Кд в соответст-
вии с исходными данными, приведенными в таблице 5.5.
Таблица 5.5 Исходные данные для расчета
Альфа (скорость дезактивации)
α
αα
α
10 см2/с
Загрязнение исходное
A0
1,00E-
07
Ки/см2
Коэффициент дезактивации исходный
Kd
10
Объем бака с раствором
V0
10000 см3
доля раствора на поверхности
ε
εε
ε
0,01 см3/см2
наносится раствора
δ
δδ
δ
0,01 см3/см2
вспомогательные величины
A0/Kd
1,00E-
08
Ки/см2
β
ββ
β
9,00E-
07
Ки/см2
γ
γγ
γ
100000 с
0,000
0,005
0,010
0,015
0,020
0,025
0,030
0,035
0 5 10 15 20 25 30
tдезактивации, час
Количество активности в емкости, Ки
t
кр
= 17,55 ч
Рисунок 5.35 – Изменение активности в емкости в ходе дезактивации
0
1
2
3
4
5
6
7
8
9
10
0 5 10 15 20 25 30
t
де зактивации
, час
Эффективный К
д
Рисунок 5.36 – Изменение эффективности дезактивации горизонтальной поверхности
Следствия из изложенной теории и рекомендации по дезактивации горизонтальных поверх-
ностей большой площади:
1. Отмывка в направлении от чистого к грязному.
2. Возможно более полное удаление дезактивирующего раствора с поверхности.
3. Обязательная промывка водой или 2-ой цикл дезактивации.
4. Для механических устройств мойки пола с зацикловкой раствора – обязательный непре-
рывный контроль загрязненности дезактивирующего раствора
.
24
Обработка лазерным лучом и сухим льдом
а б
Рисунок 5.33 – Принцип метода дезактивации путем воздействия лазерного
луча и обдувки сухим льдом (а) и используемое оборудование (б): 1 − воздуш-
ное сопло; 2 − лазер; 3 − обрабатываемый материал
Сочетание воздействия лазерного излучения и химической реакции
Удаление лакокрасочных покрытий
Лазерная дезактивация бетона
Дезактивация металлических поверхностей реактивной холодной плазмой
====================================
6. ФИЗИКО-ХИМИЧЕСКИЕ ОСНОВЫ ДЕЗАКТИВАЦИИ РАСТВО-
РАМИ. ТРЕБОВАНИЯ К ДЕЗАКТИВИРУЮЩИМ РАСТВОРАМ
N — СН2 — СН2 — N
С
О
OH
С
О
OH
С
О
OH
С
О
OH
N — СН2 — СН2 — N
С
О
OH
С
О
OH
С
О
OH
С
О
OH
С
О
OH
С
О
OH
С
О
OH
С
О
OH
С
О
OH
С
О
OH
Рис. 6.1 Структурная формула ЭДТА
Таблица 6.1. Распределение радионуклидов (°/о) между окисли-
тельным и восстановительным растворами при дезактивации
двухванным способом
Раствор
51
Cr 59
Fe
60
Со
54
Мn
1. 1% NaOH + 0,2% KMnO
4
, 24 ч 80 0,1 0,1 3,1
2. 1% (NH
4
)
2
C
2
O
4
, 24 ч 20 99,9 99,9 96,9
1, 18% NaOH + 3% КМпО
4
, 2 ч 51 11,7 4,2 28
2. 9% NH
2
SO
3
H (ингибированный), 12 ч 49 88,3 95,8 72
C
H
2
C
2
O
4
, %
0,0
0,5
1,0
1,5
2,0
2,5
024681012
С
NaOH, %
lgK
д
150
4
3
2
1
2
3
C
KMnO
4
, %
0,0
0,5
1,0
1,5
2,0
024681012
С
NaOH, %
lgW
150
4
3
2
1
2
3
C
H
2
C
2
O
4
, %
0,0
0,5
1,0
1,5
2,0
2,5
024681012
С
NaOH, %
lgK
д
150
4
3
2
1
2
3
C
KMnO
4
, %
0,0
0,5
1,0
1,5
2,0
024681012
С
NaOH, %
lgW
150
4
3
2
1
2
3
150
4
3
2
1
2
3
150
4
3
2
1
2
3
C
KMnO
4
, %
0,0
0,5
1,0
1,5
2,0
024681012
С
NaOH, %
lgW
150
4
3
2
1
2
3
C
KMnO
4
, %
0,0
0,5
1,0
1,5
2,0
024681012
С
NaOH, %
lgW
150
4
3
2
C
KMnO
4
, %
0,0
0,5
1,0
1,5
2,0
024681012
С
NaOH, %
lgW
150
4
3
2
1
2
3
Рис. 6.2. Зависимость эффективности дезактивации натурных образцов двухванным
способом (а ) и скорости растворения Cr
2
О
3
и удаления
51
Cr ( б ) от концентрации
компонентов дезактивирующих растворов
(1-й раствор: 1–10% NaOH+0,5– 5% KMn0
4
, 90–95 °С, 1 ч; 2 - й раствор: 0,5–5%
Н
2
С
2
0
4
, 90–95 °С, 1 ч):
а : 1, 3 – NaOH; 2 – Н
2
С
2
0
4
(1 – 2 цикла обработки; 2, 3 -- 1 цикл);
б : 1,3 – КМпО
4
(Cr
2
О
3
), 3 –
51
Cr); 2 – NaOH (Cr
2
О
3
)
Окислительное воздействие щелочного раствора перманганата обу-
словлено реакциями:
4МnО
4
–
+ 4ОН
–
↔4МnО
4
2–
+ О
2
+ 2Н
2
О; [ϕ = –0,564 В];
МnО
4
–
+ 2Н
2
О ↔ МnО
2
+ 4ОН
–
, [ϕ = +1,692–0,078*рН]
Окисление Сr (III) и магнетита протекает по следующим реакциям:
25
3Fe
3
О
4
+ МnО
4
–
+ 2H
2
О ↔ 3FeOOH + 3Fe
2
O
3
+MnО
2
+OH
–
[ϕFe
3
O
4
/Fe(OH)
3
= – 1,208-0,059*рН];
[ϕFе
3
о
4
/Fе
2
о
3
–0,221–0,059*рН];
Cr
2
О
3
+ МnО
4
–
+2ОН
–
↔2СrO
4
2–
+ 2МnО
2
+Н
2
О;
[ϕСr
3+
/СrO
4
2–
= 1,335 – 0,1182*рН].
Сопоставление потенциалов реакций в кислых и щелочных растворах
дает значения, приведенные в табл. 6.2.
Таблица 6.2 Потенциалы реакций (В) в кислых и щелочных рас-
творах
МnО
4
–
/ МnО
2
Сr
3+
/СrO
4
2
Fe
3
O
4
/Fe(OH)
3
Fе
3
о
4
/Fе
2
о
3
рН=1 +1,616 +1,195 -- -0,162
рН=13 +0,59 -0,20 +0,441 -0,546
0
2
4
6
8
10
12
14
12345
N, цикл
Кд
0
1
2
3
4
5
Активность
51
Cr в растворе, 10
-6
Ки/л
15 30 45 60
t, мин
1
2
3
0
2
4
6
8
10
12
14
12345
N, цикл
Кд
0
1
2
3
4
5
Активность
51
Cr в растворе, 10
-6
Ки/л
15 30 45 60
t, мин
1
2
3
Рис. 6.3. Влияние длительности обработки раствором состава 5% NaOH
4
+0,5% КМnO
4
(80–90 °С) на переход в раствор
51
Cr (2) и цикличности обработки двухванным спосо-
бом по 1 ч в каждом растворе) на дезактивацию нержавеющей стали (1) и Ст 3 (3)
7. ДЕЗАКТИВАЦИЯ ОСНОВНЫХ ЦИРКУЛЯЦИОННЫХ
КОНТУРОВ АЭС
зависимость коллективной дозы за время ремонта соотносится с общими
трудозатратами как
Д=а
1
*Т
b
(7.1)
Множитель а
1
≈ 2,0; показатель степени b ≈ 0,5. Коэффициент корреляции
такой зависимости составляет 0,97.
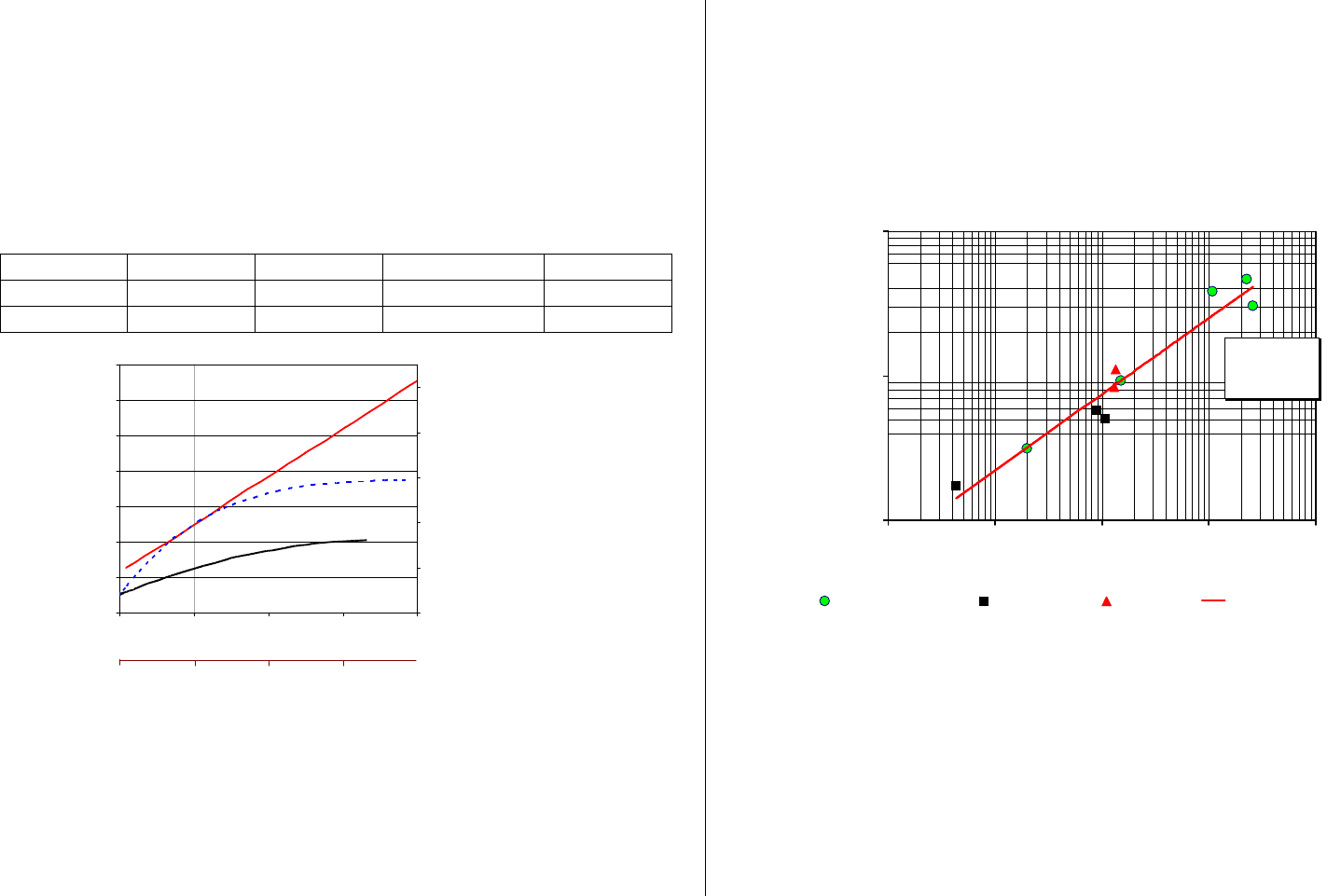
y = 1,98x
0,53
R
2
= 0,94
10
100
1000
10 100 1000 10000 100000
Трудозатраты, чел.час
Дозовые затраты, чел.сЗв
общие дозозатраты дезактивация 1,2 бл 1999 Общая линия
Рисунок 7.1 ⎯ Связь между суммарными трудозатратами на ремонт и ре-
монтными дозовыми затратами персонала ЛАЭС (суммарными трудозатрата-
ми на дезактивацию и суммарными дозовыми затратами при дезактивации)
26
2-2002
1-2004
Комплексная дезакти-
вация с применением
химреагентов
(ЛАЭС и САЭС)
Комплексная дезакти-
вация с применением
химреагентов
(ЛАЭС и САЭС)
Безреагентная или малосолевая
дезактивация (КупАЭС и САЭС)
Безреагентная или малосолевая
дезактивация (КупАЭС и САЭС)
2-2005
4-2004
4-1999
3-2001
4-2003
1-2000
3-2000
3-2005
y = 14,66e
0,004x
R
2
= 0,93
y = 23,51e
0,0072x
R
2
= 0,84
10
100
1000
10 100 1000
Количество заменяемых ТК
Коллективная доза по всем
ТК, чел.-сЗв
САЭС КАЭС ЛАЭС
ЛАЭС-3 2005 комплексная д/а малосолевая д/а
2-2002
1-2004
2-2002
1-2004
Комплексная дезакти-
вация с применением
химреагентов
(ЛАЭС и САЭС)
Комплексная дезакти-
вация с применением
химреагентов
(ЛАЭС и САЭС)
Безреагентная или малосолевая
дезактивация (КупАЭС и САЭС)
Безреагентная или малосолевая
дезактивация (КупАЭС и САЭС)
2-2005
4-2004
4-1999
3-2001
4-2003
1-2000
3-2000
3-2005
y = 14,66e
0,004x
R
2
= 0,93
y = 23,51e
0,0072x
R
2
= 0,84
10
100
1000
10 100 1000
Количество заменяемых ТК
Коллективная доза по всем
ТК, чел.-сЗв
САЭС КАЭС ЛАЭС
ЛАЭС-3 2005 комплексная д/а малосолевая д/а
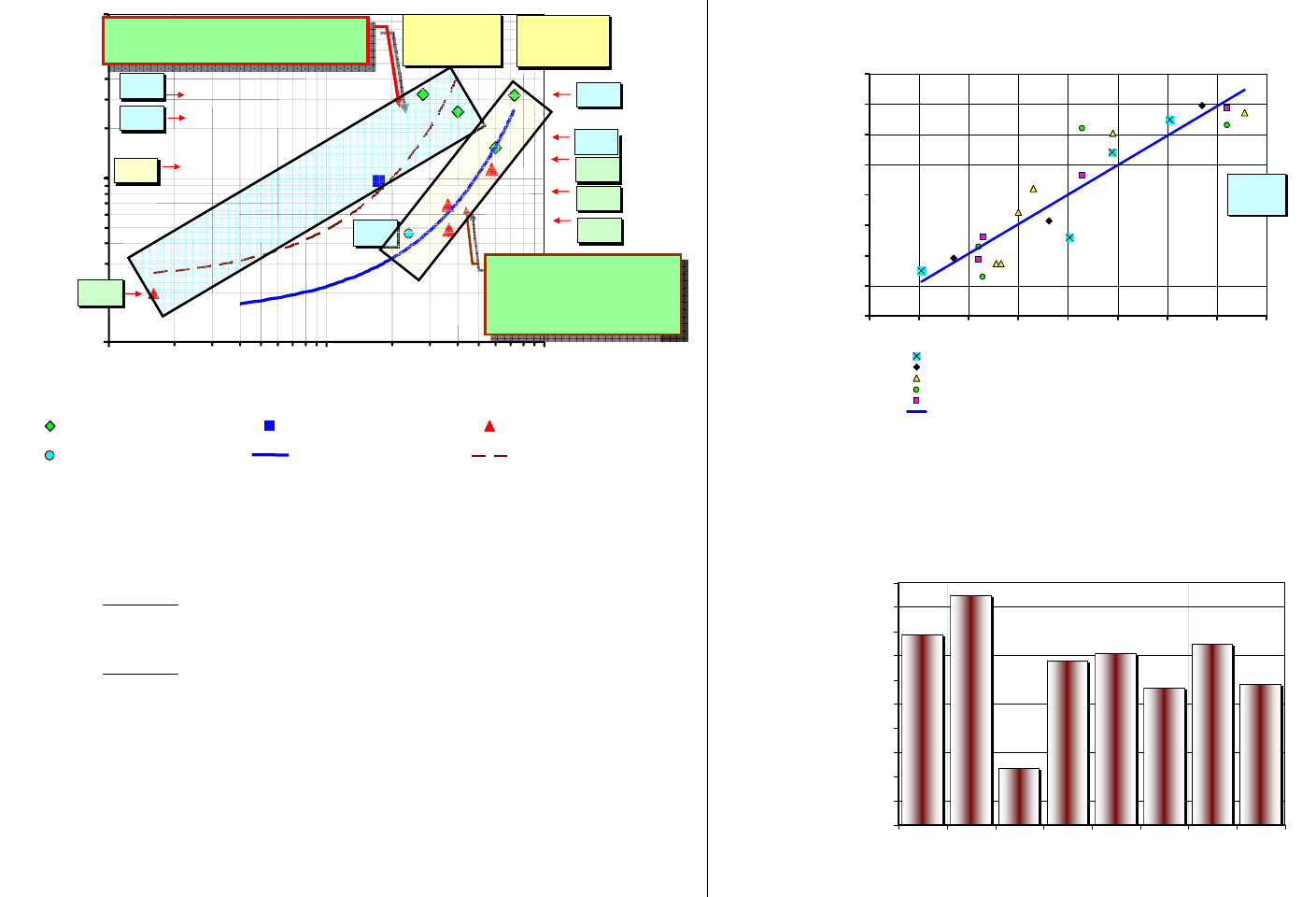
Рисунок 7.2 – Изменение дозовых затрат на замену ТК от числа
заменяемых ТК и способов проведения дезактивации
все значения укладывались на отрезке [-1; +1]:
minmax
i
i
^
ZZ
ZZ
Z
−
−
=
−
, (7.2)
minmax
i
i
^
nn
nn
n
−
−
=
−
(7.3)
где
i
^
n и
i
^
x - нормированные значения количества дефектных элементов или продуктов
коррозии железа для зависимости n
i
=f(Fe); n
i
, x
i
– среднее (для модулей СПП) или текущее
(для ТВС) количество за год на блоке дефектных элементов оборудования и вынесенного в
КМПЦ железа; соответственно,
−
n,
−
x - среднее значение для всех блоков дефектных эле-
ментов и железа для зависимости n
i
=f(Fe); соответственно n
max
, n
min
, x
max
, x
min
–
максимальное или минимальное значения количества дефектных элементов и железа для
зависимости n
i
=f(Fe).
y = 0,98x
КК = 0,92
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
-0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8
Fe
n
i
Коллективная доза при эксплуатации
Коллективная доза при капремонте
НГ ТВС
Перегрузки по парению пробок технологических каналов
Отглушенные модели сепараторов пара
Линейный (Вместе)
Рисунок 7.3 – Корреляция между нормированными значениями показателей
надежности элементов оборудования РБМК-1000, коллективными дозами и
нормируемыми значениями выноса с питательной водой железа в виде про-
дуктов коррозии
0
50
100
150
200
250
300
350
400
450
500
1995 1996 1997 1998 1999 2000 2001 2002
Год
Количество железа, поступившего в
КМПЦ за год, кг
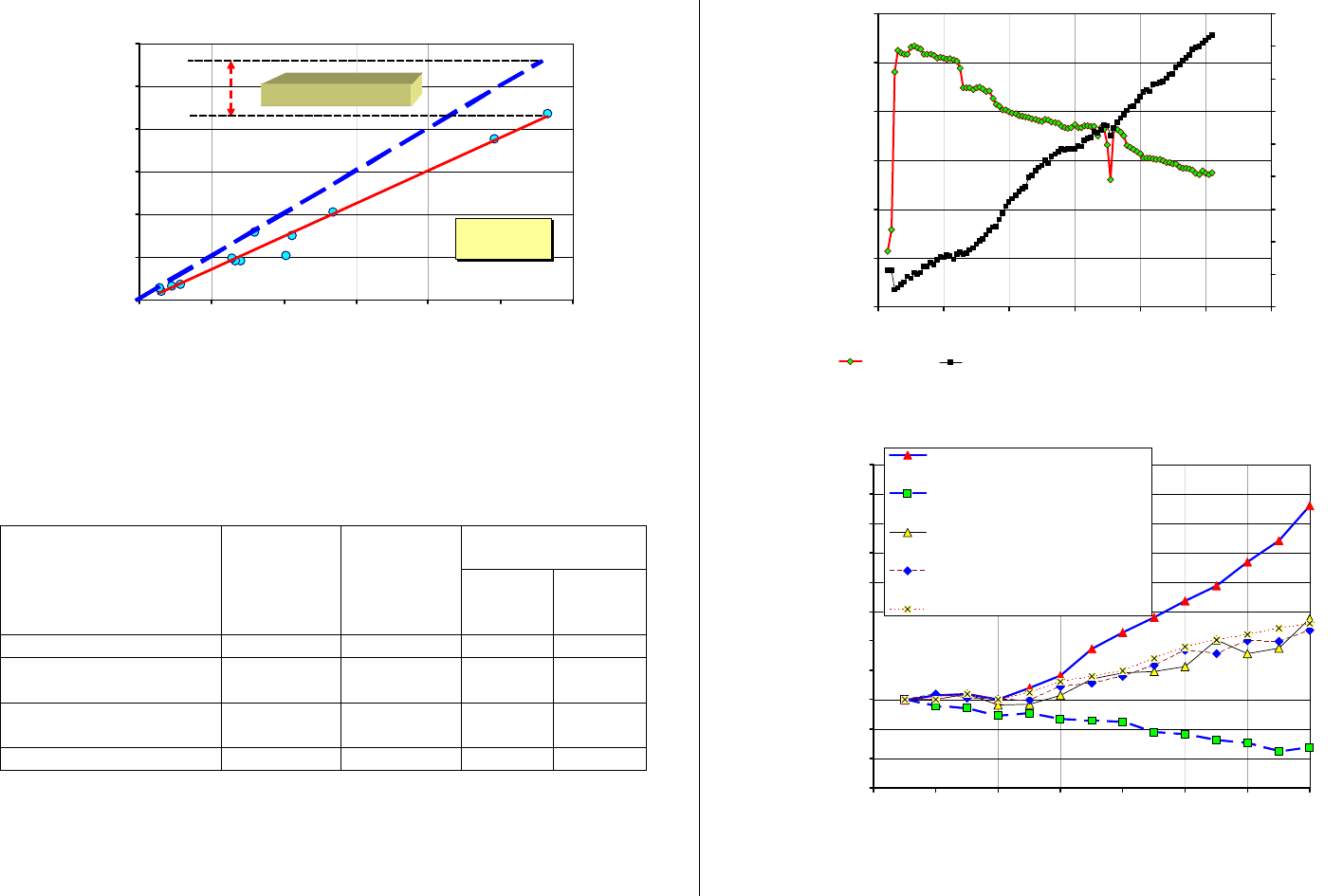
27
Рисунок 7.4 – Количество железа, поступающего из КПТ в КМПЦ за год (ЛАЭС)
y = 0,7708x - 4,727
R
2
= 0,9788
0
100
200
300
400
500
600
0 100 200 300 400 500 600
Фактические дозозатраты на 1 блоке 2004 г., мЗв
Ожидаемые фактические дозозатраты
при условии химдезактивации, мЗв
Эффект дезактивации
Рисунок 7.5 ⎯ Сравнение фактических доз и ожидаемых после дезактивации фактиче-
ских доз на 1 блоке 2004 г.
Таблица 7.1 ⎯ Фактическая коллективная доза и фактическая доза при усло-
вии проведения химической дезактивации 1 блока ЛАЭС в 2004 г.
Сэкономленная доза
%
Наименование
Фактическая
коллективная
доза
Фактическая
доза при ус-
ловии прове-
дения химде-
зактивации
мЗв %
Персонал ЛАЭС 1164 857 307 26
Привлекаемые организа-
ции
1296 978 318 25
Прочие непланируемые
дозозатраты
302 302
Итого 2762 2137 625 23
600
700
800
900
1000
1100
1200
11.7.08 31.7.08 20.8.08 9.9.08 29.9.08 19.10.08 8.11.08
Дата
Тепловая мощность реактора, МВт
2,78
2,8
2,82
2,84
2,86
2,88
2,9
2,92
2,94
2,96
Перепад давления, кг/см2
W ПДР
Рисунок 7.6 – Изменение мощности и перепад давления на реакторе 3 блока НВАЭС в
начале 34 кампании
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
3
3,5
4
02468101214
Время от начала 15 цикла, недели
Изменение температуры на выходе,
о
С
Среднее значение по 4 циркониевым
сборкам с высоким
энерговыделением
среднее значение по 4 нержавеющим
сборкам с высоким
энерговыделением, 1 цикл
2 цикл, сборка из нерж стали
2 цикл, сборка из нерж стали
3
ц
икл
,
сбо
р
ка из не
р
жавею
щ
ей стали
Рисунок 7.7 – Изменение температуры сборок различного года облуче-
ния, Loviisa 2, 1994 [23]
28
а) б)
Основной металл
Пассивный слой < 1-2 мкм
кристаллы
oxide layer ~
8-11 µm
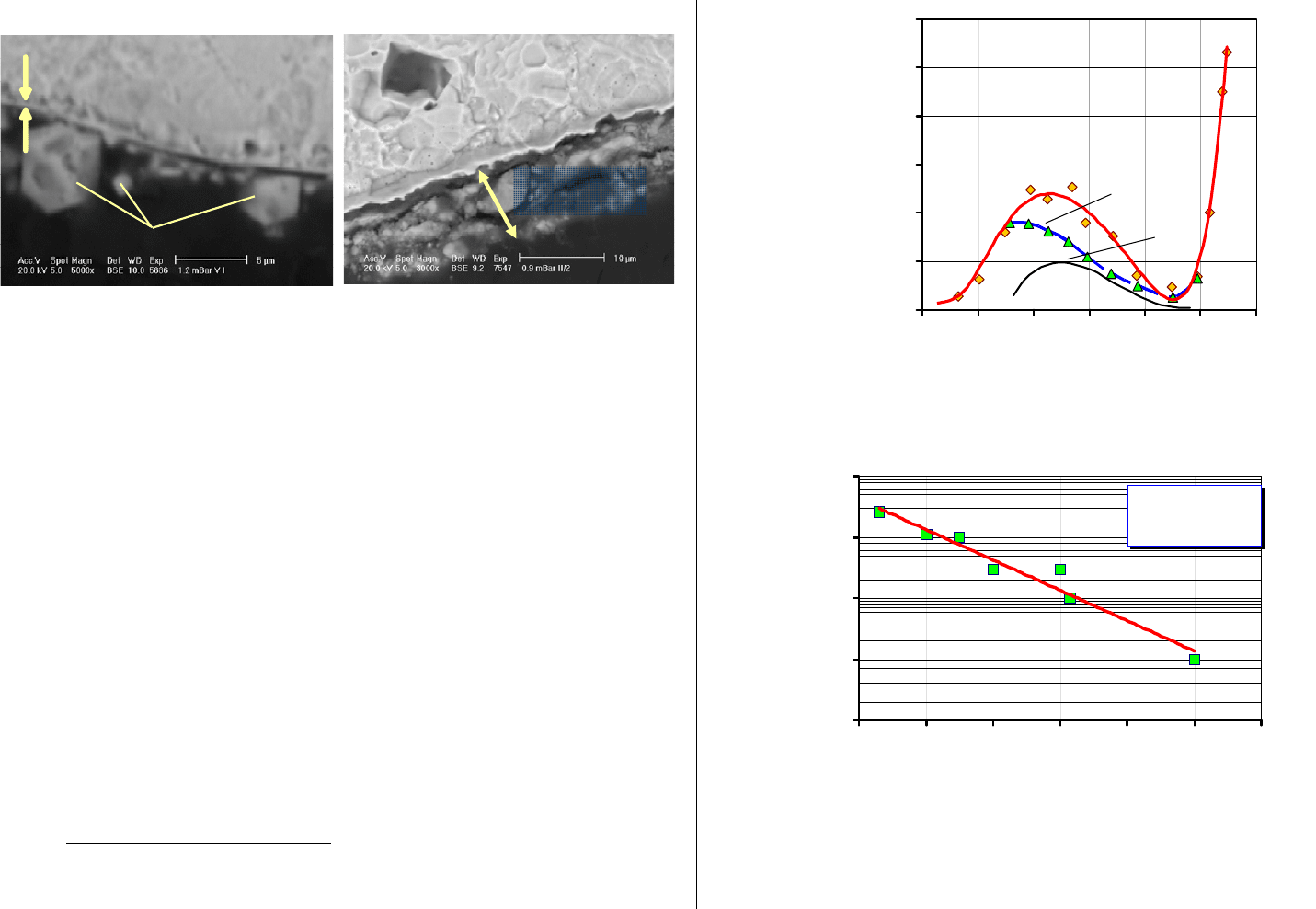
Рисунок 7.8 – а) Защитная оксидная пленка (1-2 мкм) на поверхности
стали в исходном состоянии до дезактивации;
б) Толстый рыхлый слой отложений, формирующийся на внутренней
поверхности трубок парогенератора после проведения деак-
тиваций [24]
Согласно руководящему документу РД ЭО 0047-04 [25] в настоящее время
для дезактивации контура могут использоваться только три раствора:
1) 5÷10 г/дм
3
H
2
C
2
O
4
+ 1,5÷3 г/дм
3
KNO
3
1
2) 0,3÷1 г/дм
3
H
2
C
2
O
4
+ 75÷100 мг/дм
3
НNO
3
3) 75÷100 мг/дм
3
НNO
3
Н
2
О
2
+Н
2
С
2
О
4
=2Н
2
О+2СО
2
1
На ЛАЭС используют растворы 9-10 г/л по Н
2
С
2
О
4
и 1,7-2,3 г/л азотно-
кислого калия
0
100
200
300
400
500
600
0 5 10 15 20 25 30
t, ч
Концентрация, мг/л
1
2
3
0
100
200
300
400
500
600
0 5 10 15 20 25 30
t, ч
Концентрация, мг/л
0
100
200
300
400
500
600
0 5 10 15 20 25 30
t, ч
Концентрация, мг/л
1
2
3
Рисунок 7.9 – Изменение концентрации железа в дезактивирующем растворе [26]:
1 — общее количество; 2 — растворенное железо; 3 — взвешенные продукты
y = 4,1729e
-0,5726x
R2 = 0,951
0,001
0,01
0,1
1
10
024681012
рН
Доля I
2
, %
Рисунок 7.10 – Зависимость содержания молекулярного йода (%) в воде
АЭС с РБМК при различных рН [27]
