Лекции - Автоматизация сварочных процессов
Подождите немного. Документ загружается.


21
ФЧХ. Колебательное звено создает отрицательный сдвиг фаз, который
изменяется от 0
0
при ω = 0 до –180
0
при ω = ∞. На частоте ω
с
= 1/Т ϕ (ω) = --90
0
.
4.Интегрирующее звено. Называется такое звено, выходная величина которого
пропорциональна интегралу по времени от входной величины:
х
вых
(t) = K ∫ х
вх
(t)dt .
Передаточная функция W(p) = K/p.
Переходная функция. При постоянном (ступенчатом) входном сигнале выходной
сигнал интегрирующего звена изменяется с постоянной скоростью, поэтому его
переходная функция непрерывно возрастает по линейному закону.
Отличительным свойством интегрирующего звена является то, что после
прекращения действия входного сигнала выходной сигнал звена остается на том
уровне, на котором он был в момент исчезновения входного сигнала (т. Е. Обладает
свойством запоминания последнего значения выходной величины).
Примером интегрирующего звена безинерционный электродвигатель обладает
бесконечной «памятью». Действительно, если прекратить подачу входного
напряжения, то вал двигателя остановится, и будет сохранять то угловое положение,
которое было достигнуто к моменту исчезновения напряжения.
АЧХ с ростом частоты ω убывает.
ФЧХ Звено вносит отрицательный сдвиг фаз, который не зависит от частоты и
равен -90
0
.
5.Дифференцирующее звено. Его выходная величина пропорциональна
производной по времени от выходной:
х
вых
(t) = K (dx
вх
(t)/ dt).
Примером является тахогенератор, так как его напряжение пропорционально
скорости вращения якоря, которая является производной по времени от угла поворота.
Передаточная функция W (p) = K p.
Переходная функция. Звено не пропускает постоянного по величине сигнала.
Однако при подаче на его вход ступенчатого сигнала на выходе будет импульс.
АЧХ A(ω) = K p. Имеет возрастающий характер, т.е. с увеличением частоты
увеличивается и амплитуда выходного сигнала.

22
ФЧХ Звено вносит опережение по фазе, равное +90
0
и не зависящее от частоты.
6.Запаздывающее звено. Звено, которое передает сигнал без искажений, но при
этом выходной сигнал по отношению ко входному запаздывает на постоянную
величину τ, называется запаздывающим. Таким свойством обладает, например,
релейный усилитель, причем запаздывание определяется временем срабатывания реле.
Передаточная функция W(p) = Ke
-pτ
.
Переходная функция --подобна переходной функции усилительного, но смещена
по времени на τ.
АЧХ --также подобна усилительному.
ФЧХ звено создает отрицательный сдвиг фаз, который линейно зависит от
частоты.
Табл. 1.1. Характеристики типовых звеньев автоматических систем.
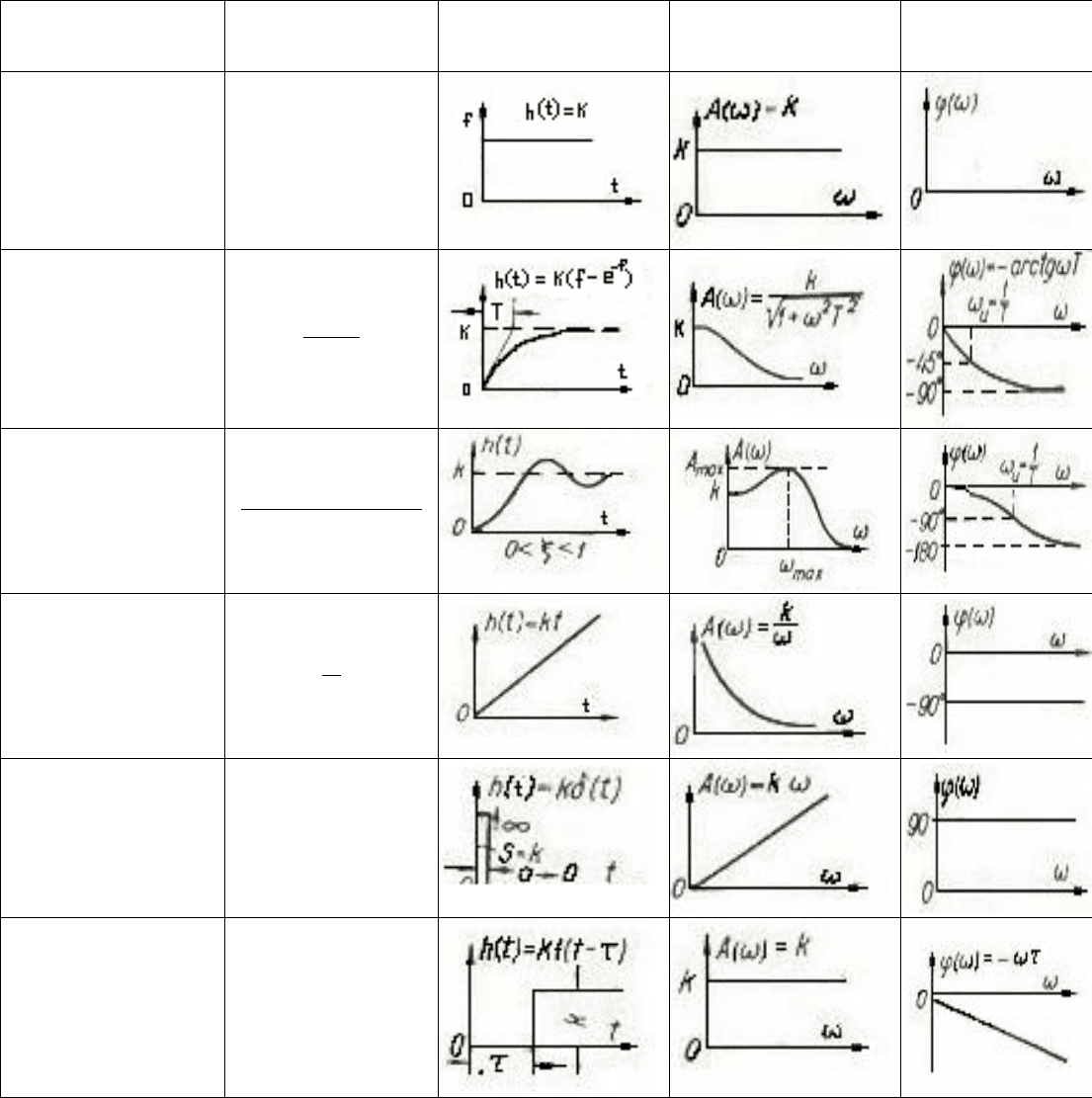
23
Тип и уравнение
звена
Придаточная
функция
Переходная
функция
Амплитудная Фазовая
Пропорциональн
ое
)
(
)
(
t
kx
t
x
nxвых
=
k
Апериодическое
вхвыхвых
kx
x
Tx
=
+
1+Tp
k
Колебательное
вх
вых
выхoвых
kx
x
xTxT
=
+
+ ε2
2
12
22
++ pTpT
k
o
ε
Интегрирующее
∫
=
t
v
вхвых dtxkx
p
k
Дифференцирую
щее
вхвых
kx
x
=
kp
Запаздывающее
)
(
)
(
τ
−
=
t
kx
t
x
вхвых
τ
p
ke
−
24
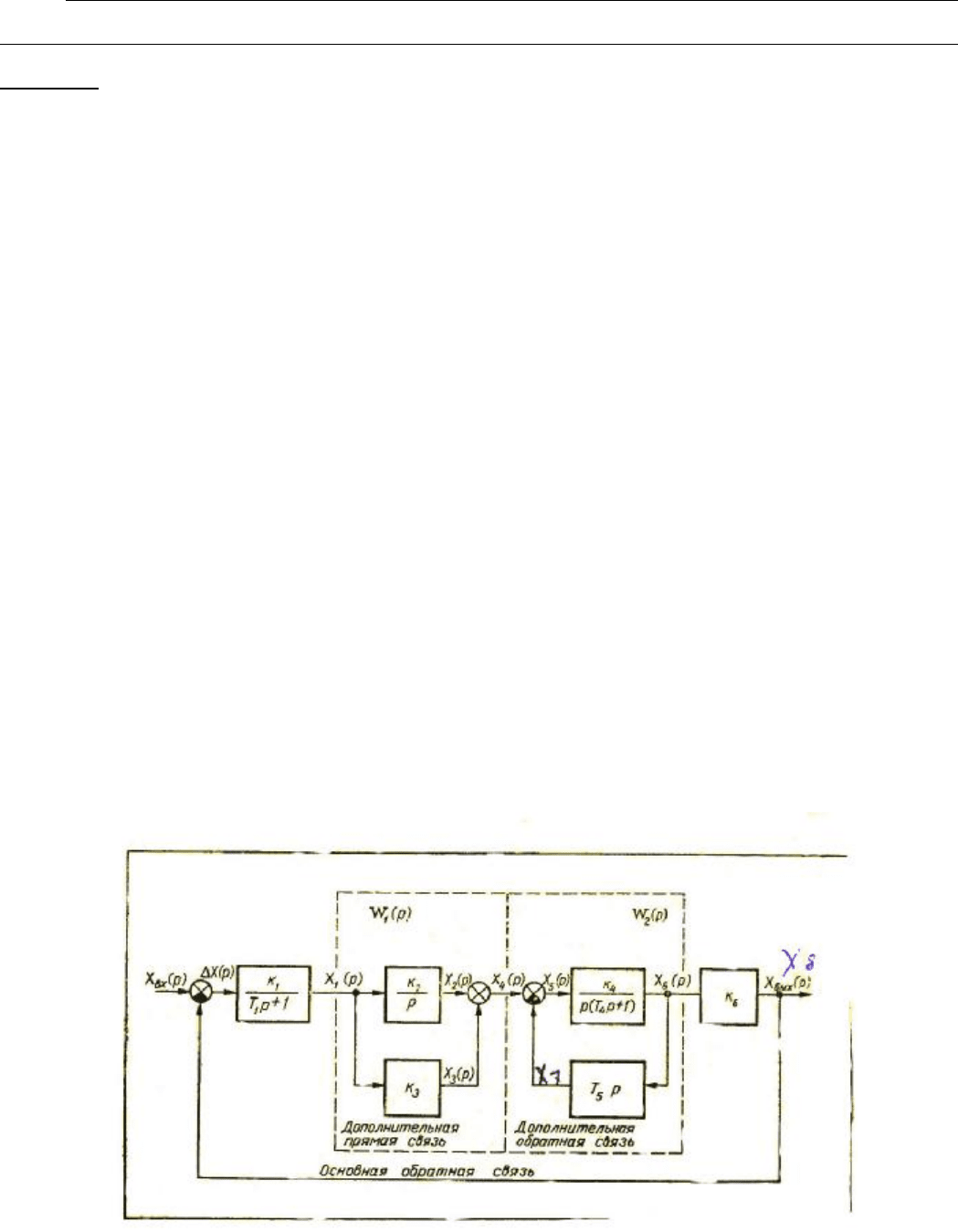
1.10 Структурная схема автоматической системы
Графическое изображение, показывающее, из каких динамических звеньев
состоит система и как они соединены между собой, наз. структурной схемой данной
системы.
Структурная схема, по существу, является графическим условным
изображением системы дифференциальных уравнений, отражающих динамику и
записанных в операторной форме по Лапласу при нулевых начальных условиях.
Основные элементы структурной схемы:
1. динамические звенья с известными передаточными функциями;
изображаются прямоугольниками, внутри которых записываются операторы
преобразования сигналов;
2.связи (соединения звеньев) – линии со стрелками, указывающими направление
передачи сигналов; различают прямые и обратные связи;
3.сумматоры, складываются или вычитаются сигналы;
4.узлы разветвления.
Непосредственно по структурной схеме можно получить уравнения системы и
наоборот. Уравнения могут быть представлены в различной форме: операторной или
дифференциальной. Для представления их в дифференциальной форме следует
выполнить переход от X(p) к x(t), а операторы р и 1/р заменить знаками производной и
интегралом.
Рис. 1.10. Структурная схема автоматической системы.

25
);()()( txtxtx
выхвх
−=∆
);()(
)(
11
1
1
txktx
dt
tdx
T ∆=+
∫
==
t
txktxdttxktx
0
133122
);()(;)()(
);()()();()()(
745324
txtxtxtxtxtx −=+=
);(
)()(
54
6
2
6
2
4
txk
dt
tdx
dt
txd
T =+
).()(;
)(
)(
66
6
57
txktx
dt
tdx
Ttx
вых
==
Исключением переменных можно разрешить эту систему уравнений
относительно любой переменной и обратным переходом получить передаточную
функцию. Решение этой задачи будет гораздо проще, если применить непосредственно
к структурной схеме правила образования передаточных функций соединений звеньев,
которые составляют основу структурного анализа.
1.11 Последовательное и параллельное соединение звеньев, обратная связь.
Основными типами соединений звеньев в автоматических системах являются
последовательное, параллельное соединение и обратная связь.
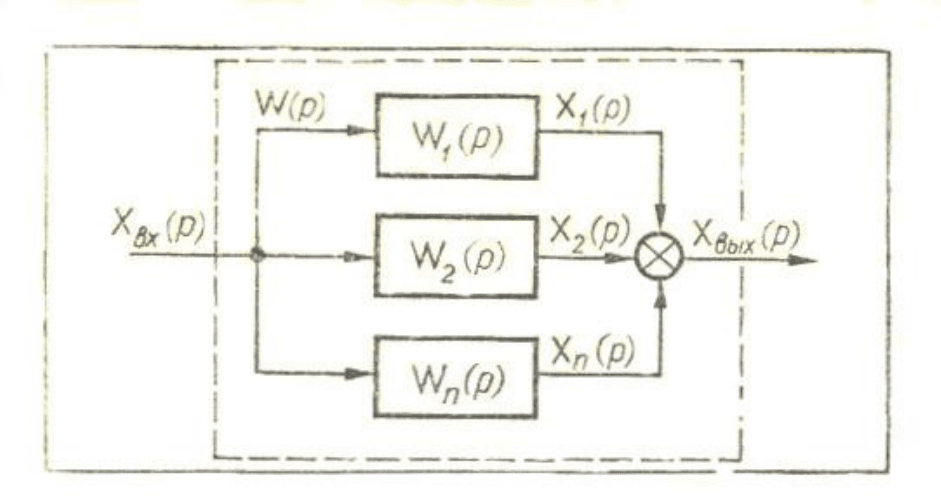
Последовательное соединение звеньев. Последовательным называется такое
соединение звеньев, при котором выход каждого предыдущего связан со входом
последующего звена (рис.1.11).
Рис. 1.11. Схема последовательного соединения звеньев.
При последовательном соединении n звеньев с передаточными функциями
W
1
(p), W
2
(p),…, W
n
(p) уравнения связи в операторной форме имеют вид:
X
1
(p) = W
1
(p)X
вх
(р);
26
X
2
(p) = W
2
(p)X
1
(p);
………………………….
Х
вых
(р) = W
n
(p)X
n-1
(p).
Исключив из данных уравнений все промежуточные переменные, кроме входной
и выходной величин, получим:
Х
вых
(р) = W
1
(p)W
2
(p)…W
n
(p)X
BX
(p).
Передаточная функция системы последовательно соединенных звеньев равна
произведению передаточных функций всех звеньев, входящих в соединение.
Амплитудно-частотная характеристика последовательно соединенных звеньев
также будет равна произведению амплитудно-частотных характеристик всех звеньев:
∏
=
=
n
i
i
AA
1
).()( ωω
Фазо-частотная характеристика равна сумме фазо-частотных характеристик всех
звеньев:
∑
=
=
n
i
i
1
).()( ωϕωϕ
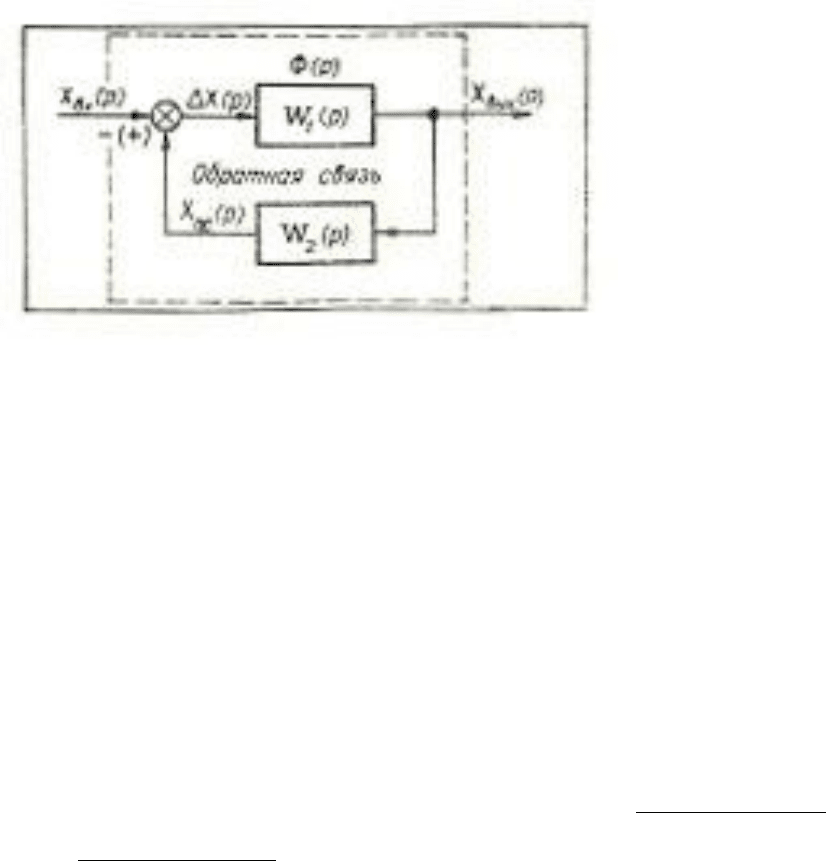
Параллельное соединение звеньев. Параллельным (согласным) называется
такое соединение звеньев, при котором входные воздействия одинаковы, а их реакции
алгебраически суммируются (рис. 1.12).
Рис. 1.12. Схема параллельного соединения звеньев.
27
Передаточная функция параллельно соединенных звеньев равна сумме
передаточных функций всех звеньев, входящих в соединение.
Обратная связь. Понятие обратная связь имеет фундаментальное значение в
теории управления. Любая автоматическая система, построенная в соответствии с
принципом управления по отклонению, имеет основную отрицательную обратную
связь. Кроме основной обратной связи, системы могут иметь дополнительные,
предназначенные для коррекции динамических свойств отдельных звеньев и системы
в целом. Обратные связи могут быть отрицательными или положительными в
зависимости от их назначения.
Обратной связью называется цепь передачи воздействий с выхода системы на ее
вход (рис.1.13).
Рис. 1.13. Структурная схема системы с обратной связью, состоящей из двух звеньев с передаточными функциями W
1
(p)
и W
2
(p).
Как видно из рисунка, выходной сигнал первого звена (реакция системы в
целом) подается на вход второго, а выходной сигнал второго звена Х
ос
с
соответствующим знаком («-« или «+») суммируется со входным сигналом системы
Х
вх
. В результате на вход первого звена, стоящего в прямой цепи системы, подается
сигнал ΔХ, равный алгебраической сумме:
ΔХ(р) = Х
вх
(р) ± Х
ос
(р).
Данное выражение называют уравнением замыкания системы (контура). Если в
правой части уравнения будет знак «-«, то обратная связь называется отрицательной,
если знак «+», то имеем положительную обратную связь.

28
Передаточная функция системы с обратной связью Φ(р), равная отношению
выходного сигнала к входному сигналу, изобразится как:
.
)()(1
)(
)(
)(
)(
21
1
pWpW
pW
рХ
рХ
р
вх
вых
±
==Φ
Здесь знак «+» относится для отрицательной обратной связи, а знак «-« -- для
положительной обратной связи.
Кроме разделения обратных связей на отрицательные и положительные, их
классифицируют и по другим признакам. В частности по виду передаточной функции
звена обратной связи.
Если в цепь обратной связи включено усилительное звено с передаточной
функцией К
ос
, то такая связь называется жесткой обратной связью.
Если в цепь обратной связи включено дифференцирующее звено с передаточной
функцией W
2
(p) = T
oc
p, то такая связь называется гибкой (дифференцирующей)
обратной связью. При этом сигнал обратной связи пропорционален производной от
выходного сигнала. Такую связь обычно применяют для того, чтобы замкнутый
контур обладал свойствами интегратора, а также с целью стабилизации систем
(получения заданного качества регулирования). Особенность гибких обратных связей
заключается в том, что воздействия передаются через них на вход системы только при
изменении сигнала Х
вых
во времени.
Обратная связь называется интегрирующей, если в ее цепь включен
интегратор. Обычно такая связь применяется при необходимости дифференцирования
задающего воздействия.
1.12 Устойчивость автоматических систем.
Любая автоматическая система, подвергаемая действию возмущающих сил,
отклоняется от равновесного состояния. При этом регулятор стремится обеспечить
заданное значение регулируемой величины и в результате чего возникает переходный
процесс.
При этом возможны три основных случая поведения системы:
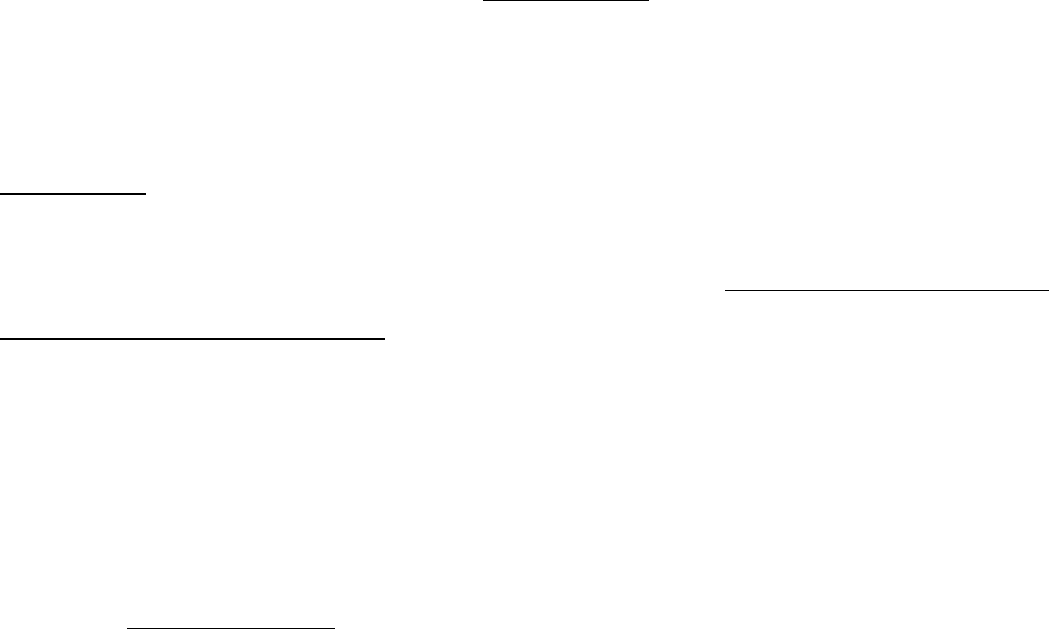
29
1) система не может восстановить равновесного состояния, значение
управляемой величины все больше отклоняется от заданного; такой процесс
называется расходящимся, а система — неустойчивой;
2) система с течением времени возвращается к равновесному состоянию,
значение управляемой величины отличается от заданного на величину статической
погрешности системы; такой переходный процесс будет сходящимся, а система—
устойчивой;
3)система характеризуется установившимся периодическим движением; такой
называется незатухающим колебательным, а система—находящейся на границе
асимптотической устойчивости.
Теорема устойчивости А. М. Ляпунова. Для того чтобы система была
устойчивой необходимо и достаточно, чтобы все корни ее характеристического
уравнения были с отрицательными вещественными частями.
Следствие.
Необходимым условием устойчивости линейной системы любого порядка
является положительность всех коэффициентов характеристического уравнения
данной системы.
Для систем первого и второго порядка данное условие является и достаточным.
Для проверки систем на устойчивость разработано несколько алгебраических
методов и на основе частотного анализа, а также на базе вычислительных методов.
Критерий Гурвица (1895г швейцарский математик)
Алгебраический критерий устойчивости в форме определителей. Используя
коэффициенты характеристического уравнения, составляют главный определитель
Гурвица. Для этого все коэффициенты, начиная с коэффициента при n—1-ой
производной, выписывают последовательно, до свободного члена по главной
диагонали. Столбцы вверх от главной диагонали дополняют коэффициентами с
возрастающими индексами, а столбцы вниз—коэффициентами с убывающими
индексами. Места, которые должны быть заняты коэффициента ми с индексом выше а
n
и ниже а
0
, заполняют нулями.
Для того чтобы характеристическое уравнение имело все корни с отрицательной
вещественной частью, главный определитель Гурвица и все его диагональные миноры
30
∇
2
, ∇
3
и т. д. должны иметь один знак с а
0
, т. е. быть больше нуля. Номер
диагонального минора определяет номер коэффициента по диагонали, для которого
составляется данный минор.
Пример:
Характеристическое уравнение:
A
0
p
5
+ A
1
p
4
+ A
2
p
3
+ A
3
p
2
+ A
4
p + A
5
= 0
53
4
1
2
0
531
420
531
0
00
0
00
00
00
AA
A
A
AA
AAA
AAA
AAA
=∇
20
31
2
AA
AA
=∇
31
420
531
3
0 AA
AAA
AAA
=∇
4
5
2
3
0
1
420
531
4
0
0
0
0
A
A
A
A
A
A
AAA
AAA
=∇
∇=∇
5
Вторая половина двадцатого века отмечена бурным развитием вычислительной
техники и численных методов. Накоплены обширные библиотеки научных программ,
в первую очередь на языке FORTRAN, предназначенных для решения типовых задач
(задачи линейной алгебры, интегрирование, решение дифференциальных уравнений и
т.д.). Кроме того, в последние годы появился целый ряд различных пакетов,
реализующих разнообразные численные методы, а также способных производить
аналитические математические преобразования, наиболее известными из которых на
сегодня являются пакеты: Mathematica (фирма Wolfram Research), Maple (фирма
Waterloo Maple Inc), MATLAB (фирма The MathWorks Inc.), Mathcad (фирма MathSoft
Inc.).
