Лебедько Е.Г. Математические основы передачи информации (части 3 и 4)
Подождите немного. Документ загружается.

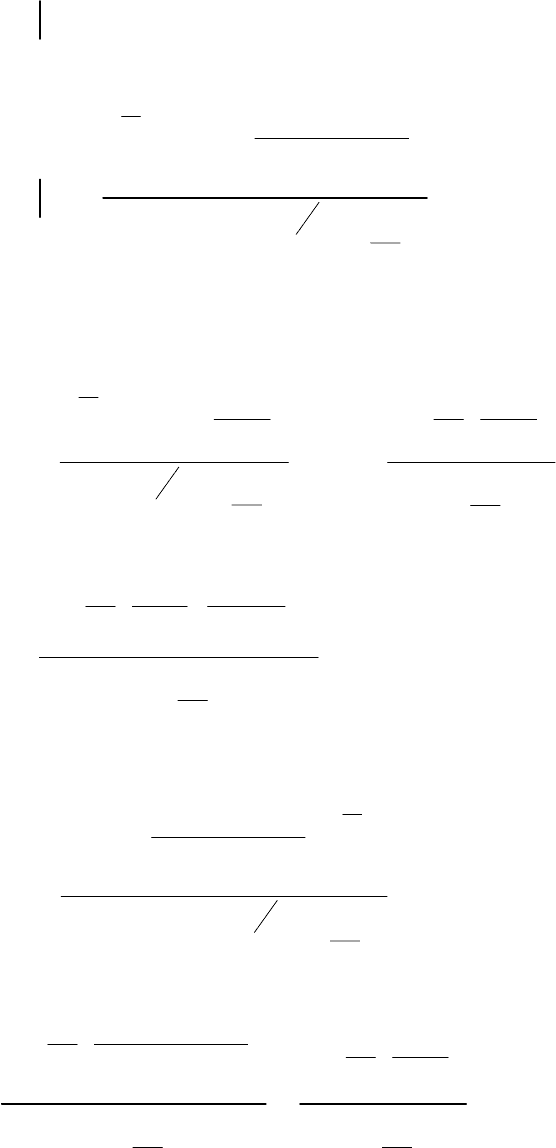
49
(
2
σ
- мощность помехи.)
Соотношение (3.121) является
распределением Пирсона
(
2
χ
-распределением).
Таким образом, плотность вероятностей выходного эффекта при
отсутствии полезного сигнала будет определяться соотношением (3.121):
()
(
)
0Wz Wz= .
Плотность вероятностей при наличии полезного сигнала
()
()
1
2
22
2
22
exp
2
2
2
N
s
N
s
z
z
Wzs
N
Г
σσ
σσ
−
⎛⎞
⎜⎟
−
⎜⎟
⎡
⎤
+
⎣
⎦
⎝⎠
=
⎛⎞
⎡⎤
+
⎜⎟
⎣⎦
⎝⎠
, (3.122)
где
2
s
σ
- мощность полезного сигнала.
Теперь условные вероятности ошибочных решений будут равны:
()
4
1
4
2
2
2
2
2
2
2
,
exp
2
2
2
1
2
22
ln 1
,
22
1 ;
2
N
N
K
K
N
z
Г
z
dz
NN
ГГ
NC
Г
N
Г
−
∞
⎛⎞
⎛⎞
−
⎜⎟ ⎜ ⎟
⎝⎠ ⎝ ⎠
==−=
⎛⎞ ⎛⎞
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
⎛⎞
⎡⎤
+
⎜⎟
⎢⎥
⎜⎟
⎣⎦
⎝⎠
=−
⎛⎞
⎜⎟
⎝⎠
∫
σ
σ
α
σ
μ
μ
(3.123)
()
4
1
2
22
2
22
0
exp
2
2
2
N
K
s
N
s
z
z
dz
N
Г
−
⎛⎞
⎜⎟
−
⎜⎟
⎡⎤
+
⎣⎦
⎝⎠
==
⎛⎞
⎡⎤
+
⎜⎟
⎣⎦
⎝⎠
∫
σσ
β
σσ
4
22
2
ln
,
,
2
2
2
2
.
22
s
K
N
NC
Г
Г
NN
ГГ
⎛⎞
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎡⎤
+
⎣⎦
⎝⎠⎝⎠
==
⎛⎞ ⎛⎞
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
σσ
μ
(3.124)
Здесь

50
()
1
0
az
Г azedz
∞
−−
=
∫
- гамма-функция;
s
σ
μ
σ
= ;
() ()
11
0
,
b
az az
b
Г ab z e dz Г azedz
∞
−− −−
==−
∫∫
- неполная
гамма-функция.
8) Обнаружение при пуассоновской статистике сигнала и помехи
Рассмотрим обнаружение слабых сигналов, что характерно для
пуассоновской статистики сигнала и помехи. Будем исходить из
предположения равномерности сигнального и помехового потоков:
()
1,0
i
i
T
gtdtN=
∫
,
(
)
1,
i
Si
T
gtdtS
=
∫
.
При слабых сигналах сумма взвешенных с постоянной величиной
независимых случайных величин, распределенных по закону Пуассона,
может рассматриваться также распределенной по закону Пуассона [3].
Тогда выходной эффект при отсутствии и наличии сигнала будет
пуассоновским с математическими ожиданиями
1
k
i
i
N
=
∑
и
1
k
i
i
S
=
∑
соответственно.
В этом случае условные вероятности ошибочных решений будут
определяться соотношениями
5
1
10
1exp
!
n
k
i
K
k
i
i
in
N
N
n
α
=
==
⎛⎞
⎜⎟
⎛⎞
⎝⎠
=− −
⎜⎟
⎝⎠
∑
∑∑
, (3.125)
()
()
5
1
10
exp
!
n
k
ii
K
k
i
ii
in
NS
NS
n
β
=
==
⎡
⎤
+
⎢
⎥
⎡⎤
⎣
⎦
=− +
⎢⎥
⎣⎦
∑
∑∑
. (3.126)
Здесь
5
1
ln
k
i
i
K
CS
=
=+
∑
- пороговый уровень обнаружителя.
9) Последетекторное обнаружение
В случае приема относительно слабого сигнала при оптимальных
правилах принятия решений (3.93) или (3.94) для определения условных
вероятностей
α
и
β
необходимо решить сложную задачу нахождения
распределения взвешенной суммы квадратов независимых случайных
величин, распределенных по обобщенному закону Релея. Однако для
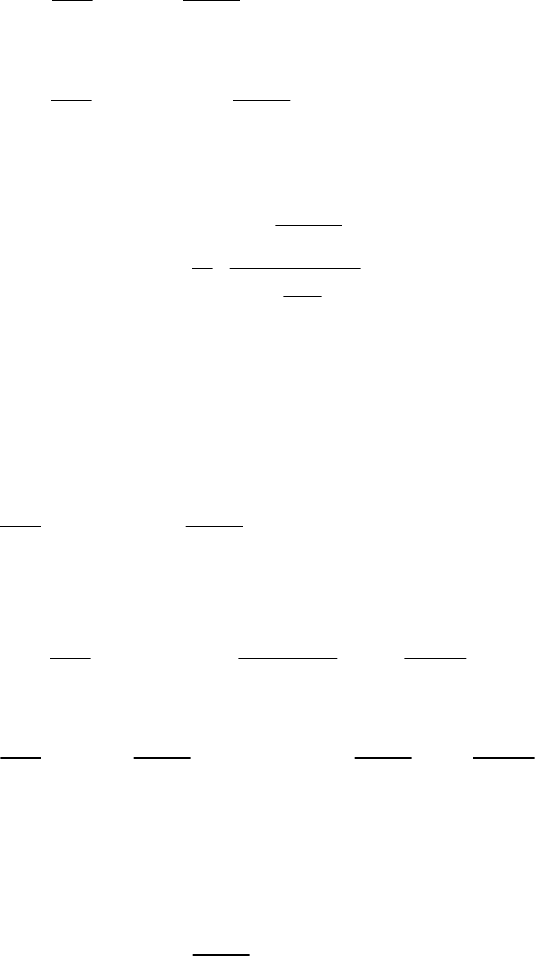
51
большого объема выборки в силу центральной предельной теоремы
распределение выходного эффекта приближенно можно считать
нормальным со следующими параметрами.
При отсутствии полезного сигнала математическое ожидание
10
m
выходного эффекта будет равно
()()
22
10 1
11
nn
ioi i i i
ii
mm ys fyWydy
∞
==
−∞
⎧⎫
==
⎨⎬
⎩⎭
∑∑
∫
. (3.127)
Так как при отсутствии сигнала
i
y распределена по релеевскому
закону
()
2
22
exp
2
ii
i
yy
Wy
σ
σ
⎛⎞
=−
⎜⎟
⎝⎠
, а
(
)
22
iii
f
yys= , то
22
322
10
22
11
0
exp 2
2
nn
oi i
iioi
ii
sy
my dys
σ
σσ
∞
==
⎛⎞
=−=
⎜⎟
⎝⎠
∑∑
∫
, (3.128)
так как
()
1
0
1
1
exp
mn
m
n
m
Г
n
tatdt
n
a
∞
+
+
⎛⎞
⎜⎟
⎝⎠
−=⋅
∫
,
(
)
Г z - гамма функция.
Дисперсия
2
M
для этого случая равна
()()
22 2
221 10
1
n
iii
i
Mmm fyWydym
∞
=
−∞
=−= − =
∑
∫
42
54444
22
111
0
exp 4 4 .
2
nnn
oi i
i i oi oi
iii
sy
ydyss
∞
===
⎛⎞
=−−=
⎜⎟
⎝⎠
∑∑∑
∫
σσ
σσ
(3.129)
При наличии полезного сигнала математическое ожидание равно
222
3
10
222
1
0
exp
2
n
oi i oi i oi
s
ii
i
sysys
my Idy
∞
=
⎛⎞
+
⎛⎞
=− =
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑
∫
σσσ
22 2
3
0
22 22
1
0
exp exp .
22
n
oi oi i i oi
ii
i
ss yys
yIdy
∞
=
⎛⎞ ⎛⎞
⎛⎞
=− −
⎜⎟ ⎜⎟
⎜⎟
⎝⎠
⎝⎠ ⎝⎠
∑
∫
σσ σσ
Используя асимптотическое представление модифицированной
функции Бесселя (3.91) и ограничиваясь двумя первыми членами
разложения в степенной ряд экспоненты, получим
2
22
1
2
1
3
21
2
n
oi
soi
i
s
ms
σ
σ
=
⎡⎤
≈+
⎢⎥
⎣⎦
∑
. (3.130)
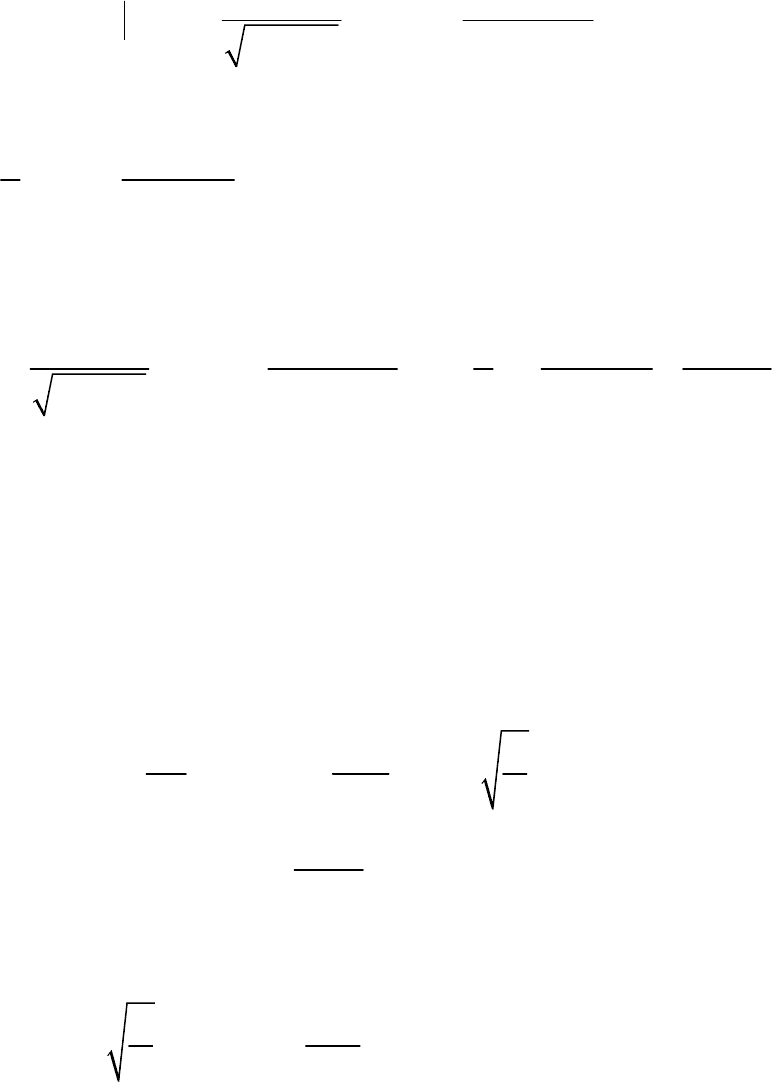
52
Дисперсия
2
s
M
для данного случая будет определяться также
приближенной зависимостью
44
2
1
4
n
s
oi
i
M
s
σ
=
≈
∑
. (3.131)
Таким образом, при приеме относительно слабых сигналов условные
вероятности ошибочных решений с учетом соотношений (3.128), (3.129),
(3.130) и (3.131) будут определяться формулами
()
()
66
2
10
20
20
2
2
1
1
0exp
2
2
12ln
1 ;
2
KK
n
oi
i
zm
W z dz dz
M
M
C
Ф
s
∞∞
=
⎡⎤
−
⎢⎥
== − =
⎢⎥
⎣⎦
⎡⎤
⎛⎞
⎢⎥
⎜⎟
⎢⎥
⎜⎟
=−
⎢⎥
⎜⎟
⎢⎥
⎜⎟
⎝⎠
⎣⎦
∫∫
∑
α
π
σ
(3.132)
()
6
2
2
2
1
1
2
2
2
2
0
1
3
112ln
exp
22
2
2
n
K
oi
s
i
n
s
s
oi
i
s
zm
C
dz Ф
M
M
s
σ
β
σ
π
=
=
⎛⎞
⎜⎟
⎡⎤
−
⎜⎟
⎢⎥
=−=−
⎜⎟
⎢⎥
⎣⎦
⎜⎟
⎝⎠
∑
∫
∑
(3.133)
При приеме относительно сильных сигналов в условиях
правомерности правил принятия решений (3.96) или (3.97) в силу
центральной предельной теоремы распределение выходного эффекта
также можно считать нормальным с параметрами:
- при отсутствии полезного сигнала математическое ожидание
10
m
∗
и
дисперсия
20
M
∗
равными
2
2
10
22
11
0
exp
2
2
nn
oi i
iioi
ii
sy
my dys
π
σ
σσ
∞
∗
==
⎛⎞
=−=
⎜⎟
⎝⎠
∑∑
∫
, (3.134)
22 2
20 2 1
1
4
2
n
oi
i
M
mm s
π
σ
∗
=
−
=−=
∑
; (3.135)
- при наличии полезного сигнала моменты
1
s
m
∗
2
s
M
∗
будут
определяться выражениями
4
1
4
1
3
1
2
8
n
oi
soi
i
s
ms
π
σ
σ
∗
=
⎛⎞
≈−
⎜⎟
⎝⎠
∑
, (3.136)

53
22
2
1
4
2
n
s
oi
i
M
s
π
σ
∗
=
−
≈
∑
. (3.137)
Условные вероятности ошибочных решений будут равны:
710
20
1
1
2
Km
Ф
M
α
∗
∗
⎡⎤
⎛⎞
−
⎢⎥
⎜⎟
=−
⎜⎟
⎢⎥
⎝⎠
⎣⎦
, (3.138)
71
2
1
2
s
s
Km
Ф
M
β
∗
∗
⎛⎞
−
⎜⎟
=
⎜⎟
⎝⎠
. (3.139)
В этих формулах моменты
10
m
∗
,
20
M
∗
,
1
s
m
∗
и
2
s
M
∗
определяются
соотношениями (3.134)-(3.137).
3.1.10. Последовательное обнаружение
Классическая процедура принятия решений предполагала, что время,
за которое принимается решение, заведомо известно объемом
наблюдаемой выборки и фиксировано. Оно определяется длительностью
полезного сигнала. В ряде случаев принимаемая реализация
()
yt может
оказаться настолько благоприятной, что принятие решения можно
произвести значительно быстрее, чем это предусматривается классической
процедурой. В этом случае риск обусловлен не только ошибочными
решениями, но и объемом выборки. Такой подход приводит к
процедуре
Вальда или последовательной проверке гипотез, при которой анализ
проводится последовательно при получении очередного отсчета. При
этом все пространство наблюдений делится уже не на две области, как при
классической процедуре принятия решений, а на три:
0
Г - область
принятия решения об отсутствии сигнала,
1
Г - область принятия решения
о наличии полезного сигнала,
н
Г - область неопределенности. В общем
случае границы между этими областями могут меняться на каждом этапе
наблюдения.
При последовательном анализе на каждом этапе составляется
отношение правдоподобия
()
(
)
()
()
()
,
0
m
m
m
Wy s
Wy
Λ=
где m- номер отсчета.
В отличие от однопорогового обнаружения (классическая процедура)
последовательная процедура является двухпороговой. Величина
(
)
m
Λ
сравнивается с двумя пороговыми уровнями – с
A
и с B .

54
Правило принятия решения при последовательной процедуре
записывается в виде
()
()
()
()
()
()
()
()
()
()
()
()
()
()
1
0
1
0
0
0
0
m
H
m
m
m
H
m
m
m
н
m
Wy s
A
Wy
Wy s
B
Wy
Wy s
BA
Wy
γ
γ
γ
⎧
⎪
Λ= ≥→
⎪
⎪
⎪
⎪
⎪
Λ= ≤→
⎨
⎪
⎪
⎪
⎪
<>→
⎪
⎪
⎩
. (3.140)
Здесь
н
γ
- решение о продолжении наблюдения.
Если выборка
()
m
y
наблюдения попадает в область
н
Г между
пороговыми уровнями
A
и B , то принимается решение
н
γ
о продолжении
наблюдения и формировании отношения правдоподобия
(
)
1m
+
Λ ;
процедура принятия решения повторяется до тех пор, пока отношение
правдоподобия не окажется выше уровня
A
или ниже уровня B . В
результате длительность наблюдения
н
τ
(время, в течение которого
принимается решения
0
γ
или
1
γ
.) является случайной величиной.
Определим пороговые уровни
A
и B, исходя из предположения, что
известны условные вероятности ошибочных решений
α
и
β
. Условие
принятия решения
1
γ
согласно (3.140) будет
()
()
()
()
1
0
m
H
m
Wy s
A
Wy
Λ= ≥
или
()
()
()
()
0
mm
Wy s AWy≥ . (3.141)
Это условие относится к любой выборке, попадающей в область
1
Г .
Поэтому можно проинтегрировать обе части неравенства (3.141) по
области
1
Г :
()
()
()
(
)
11
0
mm
ГГ
Wy sdy AWy dy≥
∫∫
. (3.142)

55
Интеграл в левой части неравенства (3.142) представляет собой, в
соответствии с выражением (3.16), вероятность правильного обнаружения
(мощность решения)
1
d
, т.е.
()
()
1
1
1
m
Г
Wy sdy d
β
==−
∫
,
а интеграл в правой части – условную вероятность ошибки первого рода
(вероятность ложной тревоги)
α
:
()
()
1
0
m
Г
Wy dy
α
=
∫
.
Следовательно,
1
A
β
α
−
≤
. (3.143)
Условие принятие решения
0
γ
будет
()
()
()
()
0
m
m
Wy s
B
Wy
≤
или
()
()
()
()
0
mm
Wy s BWy≤ . (3.144)
Проинтегрировав обе части неравенства (3.144) по области
0
Г
, находим,
что
1
B
β
α
≥
−
, (3.145)
так как
()
()
0
m
Г
Wy sdy
β
=
∫
, а
()
()
0
0
01
m
Г
Wy dy d
α
==−
∫
.
Следует отметить, что формулы (3.143) и (3.145) относятся к
значениям
0,5
α
< и 0,5
β
< [5]. Однако описанным методом можно
получить и более общие формулы
1
max ,
1
A
β
β
α
α
−
⎛⎞
≤
⎜⎟
−
⎝⎠
и
1
min ,
1
B
β
β
αα
−
⎛⎞
≥
⎜⎟
−
⎝⎠
.
Границы
A
и B являются функциями аргументов
α
и
β
. Однако
оказывается, что в качестве хорошего приближения для
A
и B можно
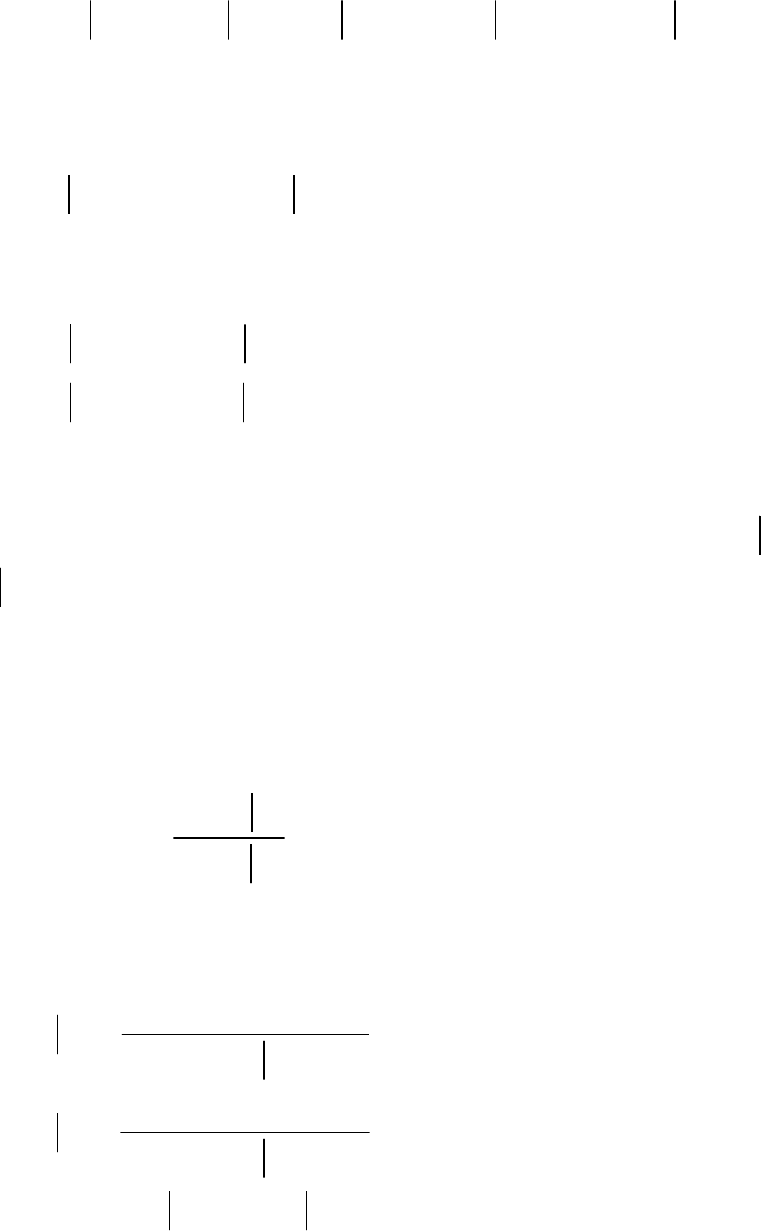
56
взять их граничные значения, соответствующие знакам равенства в
формулах (3.143) и (3.145).
Для статистически независимых и однородных наблюдений
12
,,...
m
yy y
()
()
()() () ()
12
1
m
m
mi
i
Wy s WysWys Wy s Wys
=
= ⋅⋅⋅ =
∏
. (3.146)
В этом случае последовательный обнаружитель, реализующий
правило принятия решения (3.140), является оптимальным в том смысле,
что он минимизирует среднее время принятия решения
н
τ
:
{
}
1
0min
н
m
τ
= ,
{
}
1
min
н
ms
τ
= ,
в классе всех обнаружителей, для которых условные вероятности
ошибочных решений ограничены заданными величинами.
Среднее время принятия решения можно представить в виде
{
}
{
}
{} {}
11
11
0 0,
,
н
н
mtmn
mstmns
=Δ
=Δ
τ
τ
(3.147)
где
tΔ - длительность ступени наблюдения (минимальный интервал
между соседними выборочными значениями реализации
(
)
yt, при
котором эти значения можно считать независимыми),
{
}
1
0mn и
{
}
1
mns - средние объемы выборки при отсутствии и наличии полезного
сигнала соответственно.
Ввиду того, что минимизация среднего времени принятия решения
оптимизирует правило принятия решения, определим это среднее значение
н
τ
или, согласно (3.147), средний объем выборки.
Перейдем, с учетом (3.146), к логарифму отношения правдоподобия:
()
()
()
11
ln ln
0
mm
i
m
i
ii
i
Wys
z
Wy
==
Λ= =
∑∑
,
который сравнивается с
ln
A
и ln B .
Средний объем выборки при отсутствии и наличии полезного сигнала
определяется соответственно формулами:
{}
()
{}
1
1
ln 1 ln
0
0
A
B
mn
mz
α
α
+−
=
, (3.148)
{}
()
{}
1
1
ln 1 lnBA
mns
mzs
β
β
+−
=
, (3.149)
где величины
{
}
1
0mz и
{
}
1
mzs определяются соотношениями
57
{}
()
()
()
1
1
0ln 0
0
m
i
ii
i
i
Wys
mz Wy dy
Wy
∞
=
−∞
⎡⎤
=
⎢⎥
⎢⎥
⎣⎦
∑
∫
, (3.150)
{}
()
()
()
1
1
ln
0
m
i
ii
i
i
Wys
mzs Wysdy
Wy
∞
=
−∞
⎡⎤
=
⎢⎥
⎢⎥
⎣⎦
∑
∫
. (3.151)
При малых значениях условных вероятностей принятия решений
(
0,1
α
< и 0,1
β
< ), как следует из (3.143), (3.145), (3.148) и (3.149),
можно определять
{
}
1
0mn и
{
}
1
mns по формулам
{}
{}
{}
{}
11
11
ln ln
0,
0
mn mns
mz mzs
≈≈−
β
α
. (3.152)
Для дисперсий объемов выборок
2
0
n
σ
и
2
ns
σ
при малых
α
и
β
справедливы следующие приближенные формулы [6]:
{}
2
0
2
0
3
1
ln
0
z
n
B
mz
σ
σ
≈ ,
{}
2
2
3
1
ln
zs
ns
A
mzs
σ
σ
≈ . (3.153)
В этих формулах
{
}
{
}
22
21
0
00
z
mz mz
σ
=−,
{}
()
()
()
2
1
1
0ln 0
0
m
i
ii
i
i
Wys
mz Wy dy
Wy
∞
=
−∞
⎡⎤
=
⎢⎥
⎢⎥
⎣⎦
∑
∫
,
{
}
{
}
22
21
zs
mzs mzs
σ
=−,
{}
()
()
()
2
1
1
ln
0
m
i
ii
i
i
Wys
mzs Wysdy
Wy
∞
=
−∞
⎡⎤
=
⎢⎥
⎢⎥
⎣⎦
∑
∫
.
Приведенные соотношения позволяют рассчитать основные
характеристики оптимального последовательного обнаружителя.
Однако следует заметить, что последовательная процедура принятия
решений
дает выигрыш по отношению к классической в среднем времени
принятия решения
. В отдельных случаях выходной эффект может долго
находиться между пороговыми уровнями
A
и B , и время принятия
решения может оказаться недопустимо большим. Этот недостаток
устраняется применением усеченной последовательной процедуры, в
которой через определенный заданный промежуток времени
осуществляется переключение на однопороговую систему.
58
3.2. ЭЛЕМЕНТЫ ТЕОРИИ ФИЛЬТРАЦИИ СИГНАЛОВ
В статистической теории приема сигналов на фоне помех
рассматривают две группы задач: а) обнаружение сигналов на фоне
помехи; б) выделение сигналов из помехи. В первом случае точное
воспроизведение сигнала не играет роли, но требуется с максимальной
надежностью вынести решение о наличии или отсутствии сигнала. Во
втором случае необходимо с минимальными искажениями
воспроизвести
сигнал.
Если спектральная функция полезного сигнала и энергетический
спектр помехи различаются, то для решения этих задач естественно
использовать фильтры, в которых подбирают передаточную функцию
таким образом, что подавляются спектральные компоненты помехи и
одновременно выделяются спектральные компоненты полезного сигнала.
Рассматривают два вида фильтрации: а) фильтрация с позиции максимума
отношения сигнала
к помехи; б) фильтрация с позиции минимума
искажения полезного сигнала. Рассмотрим сначала фильтрацию с позиции
максимума отношения сигнала к помехе.
3.2.1. Оптимальная линейная фильтрация с позиции максимума
отношения сигнала к помехе
В рассмотренных выше оптимальных обнаружителях принимаемая
реализация поступает на вход схемы оптимальной обработки смеси
сигнала с помехой. При этом для большинства этих обнаружителей
оптимальная обработка осуществляется взаимно-корреляционным
устройством, содержащим перемножитель и интегратор.
Взаимная корреляционная функция на выходе схемы обработки смеси
сигнала с помехой в общем виде может быть представлена зависимостью
() ( ) ( )
,
s
T
Bt yt ttdt
ϑ
′
′′
=
∫
.
С учетом временной задержки
τ
принимаемого сигнала это
соотношение можно переписать в виде
() ( ) ( )
s
T
Bt yt t t dt
ϑτ
′
′′
=−+
∫
. (3.154)
В формуле (3.154)
()
yt
′
- входная реализация, а
()
t
ϑ
′
- весовая
функция, определяемая решением интегрального уравнения Фредгольма
1-го рода
( )() ()
2
0
,
T
B
tdst
τϑτ τ
=
∫
. (3.155)
Приведенные выше структурные схемы взаимно-корреляционных
устройств не обладают инвариантностью по отношению ко времени
