Лебедева Н.С. Методическое пособие по программированию на Turbo Prolog

Подождите немного. Документ загружается.

Правило average_mark состоит из четырех подцелей:

первая подцель – содержит предикат findall, который формирует список

Mark_list

из базы данных, просматривая все

утверждения с предикатом mark. Значения Mark,

взятое предикатом findall из первого утверждения

предиката mark, присваивается голове списка

Mark_list = [7],

остальные значения mark помещаются в хвост

Mark_list=[7, 9, 5, ...];

вторая подцель – вычисляет сумму баллов, количество студентов и

представляет собой рекурсивную процедуру,

состоящую из факта (1) и рекурсивного правила (2).

Факт (1) представляет выход из рекурсии – базовое

состояние рекурсии. Рекурсия происходит до тех

пор, пока список mark_list не станет пустым.

Mark_list = [ ],

переменные SUM1 = 0, Number1 = 0.

Из стека последовательно извлекаются элементы

списка Mark_list(H) и суммируются

SUM = H + SUM1,

и на каждом шаге обратной рекурсии переменная

Number увеличивается на единицу;

третья подцель – вычисляет среднее значение баллов;

четвертая подцель – выводит на печать значение среднего балла, которое

содержит переменная Average.

5. Деревья

5.1. Основные понятия

Структура, из каждой вершины которой отходит несколько ветвей к

следующим вершинам, называется деревом. Дерево, имеющее степень

узлов, равную 2, называется бинарным или двоичным деревом.

Двоичное дерево либо пусто, либо состоит из следующих трех частей:

корень дерева;

левое поддерево;

правое поддерево.

Поддеревья сами должны быть двоичными деревьями.

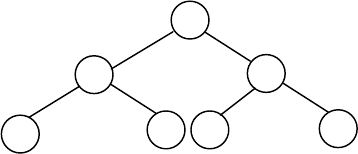
Рис.5.1. Пример двоичного дерева

Деревья часто используются для представления других структур

данных, например, списков, множеств и для поиска элементов.

Эффективность поиска можно улучшить, если между элементами дерева

установить отношения порядка. Тогда можно элементы в дереве

упорядочить слева направо в соответствии с этим отношением.

Упорядочивание может производится либо в алфавитном порядке,

либо в числовом порядке, либо в порядке более сложном (по частям

элементов или их величине).

Непустое дерево упорядочено слева направо, если:

все вершины левого поддерева меньше корня дерева;

все вершины правого поддерева больше корня дерева;

оба поддерева упорядочены.

Такое двоичное дерево называется упорядоченным деревом, или

двоичным справочником. Экономия при поиске достигается за счет

того, что достаточно просмотреть не более одного поддерева.

4 87

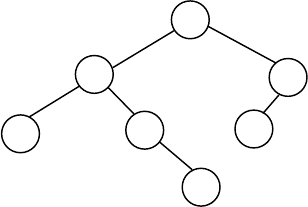
Рис.5.2. Пример упорядоченного двоичного дерева

Деревья в Турбо-Прологе являются динамическими структурами

данных. Далее будут рассмотрены двоичные упорядоченные деревья.

Для задания дерева в программе необходимо в разделе доменов

описать домен дерева. Например, дерево на рис. 5.2 можно описать так:

domains

treetype = tr (integer, treetype, treetype); empty, 

где treetype – имя домена, определяемое пользователем;

tr(integer, treetype, treetype) – функтор, имя которого и порядок

объектов определяет пользователь;

empty – пустой функтор, имя функтора определяет пользователь.

В общем виде можно записать так:

tr( X, L, R),

где X – корень дерева;

L – левое поддерево;

R – правое поддерево.

Основные операции, выполняемые над деревьями :

1. Поиск элементов в дереве (принадлежность дереву).

2. Добавление нового элемента в дерево на любой уровень.

3. Удаление элемента дерева с любого уровня.

5.2. Основные операции над деревьями

5.2.1. Поиск элемента в дереве

Для того, чтобы найти элемент Х в дереве, необходимо рассмотреть

три случая:

1) элемент Х совпадает с конем дерева;

2) элемент Х больше значения корня дерева, то искать элемент Х в

правом поддереве;

3) элемент Х меньше значения корня, то искать в левом поддереве.

Рассмотрим процедуру поиска:

find_tree(X, tr(X, _, _)). (1)

find_tree (X, tr(Y, L, _)):– (2)

X < Y,

find_tree(X, L).

find_tree(X, tr(Y, _, R)):– (3)

X > Y,

find_tree(X, R).

Предикат find_tree имеет два объекта: элемент Х и заданное дерево. Если

элемент Х присутствует в дереве, работа данной процедуры будет успешна.

Поиск элемента в дереве окончен, когда дерево будет пустым.

Процедура состоит из факта (1) и двух рекурсивных правил. Факт (1)

отражает присутствие элемента в дереве. Случай, когда элемент Х совпадает с

корнем дерева. Правило (2) – поиск элемента в левом поддереве find_tree(X, L).

Правило (3) – поиск элемента в правом поддереве find_tree (R, L).

Поиск в двоичном справочнике эффективнее, чем поиск в списке. Время

поиска будет пропорционально глубине дерева. Глубина дерева – это длина

самого длинного пути между корнем и листом дерева.

5.5.2.Добавление нового элемента в дерево

Добавление нового элемента в дерево в качестве листа

Самый простой способ добавить новый элемент на самый нижний уровень

дерева в качестве листа. Место, куда помещается новый элемент, выбрать таким

образом, чтобы не нарушить упорядоченность дерева. Двоичное упорядоченное

дерево не должно содержать одинаковые элементы.

Рассмотрим процедуру добавления нового элемента в качестве листа.

add_leaf(empty, X, tr(X, empty, empty)). (1)

add_leaf(tr(X, L, R), X, tr(X, L, R)). (2)

add_leaf(tr(Y, L, R), X, tr(Y, L1, R)):– (3)

X < Y,

add_leaf(L, X, L1). 

add_leaf(tr(Y, L, R), X, tr(Y, L, R1)):– (4)

X > Y,

add_leaf(R, X, R1).

Предикат add_leaf имеет три объекта:

первый объект -- входное дерево;

второй объект – элемент, добавляемый в дерево (Х);

третий объект – выходное дерево.

Процедура добавления содержит: два факта (1), (2) и два рекурсивных

правила (3) и (4).

Факт (1) показывает, что если дерево пустое, то новый элемент добав-

ляется на место корня. Этот факт и дает выход из данной процедуры.

Факт (2) показывает, что добавляемый элемент совпадает с корнем

дерева. Входное дерево и выходное дерево совпадают.

Правило (3) содержит входное дерево tr(Y, L, R) и выходное дерево

tr(Y, L1, R). Видно, что эти два дерева отличаются своими левыми

поддеревьями (L и L1). Это значит, что новый элемент добавляется в

левое поддерево, если X < Y, где Y – корень входного дерева. Правило

(4) работает аналогично правилу (3), только добавление происходит в

правое поддерево.

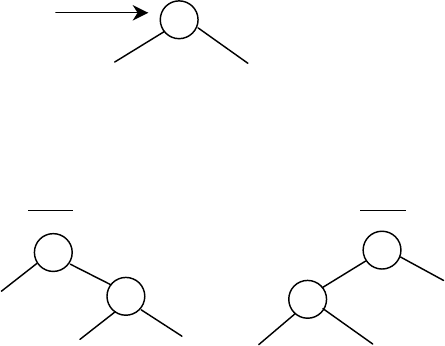
Добавление нового элемента в дерево на место корня

Имеем дерево:

где Y – корень дерева или внутренняя вершина дерева;

X – новый элемент вместо Y.

Имеем два случая:

Рис. 5.3 Добавление нового элемента Х в качестве корня

Требования к поддеревьям L1 и L2 (или, соответственно к R1и R2):

1. L1 и L2 – двоичные упорядоченные деревья.

2. Множество вершин L1 и L2 совпадает с L.

3. Все вершины из L1 меньше, чем Х.

4. Все вершины из L2 больше, чем Х.

X < Y

X > Y

вставить

Отношения, которые способно наложить все эти требования на L1

и L2 (соответственно на R1 и R2): L1, L2 (R1, R2) должны быть такими,

чтобы достигалась цель

add_root(L, X, tr(X, L1, L2)) 

add_root(R, X, tr(X, R1, R2)).

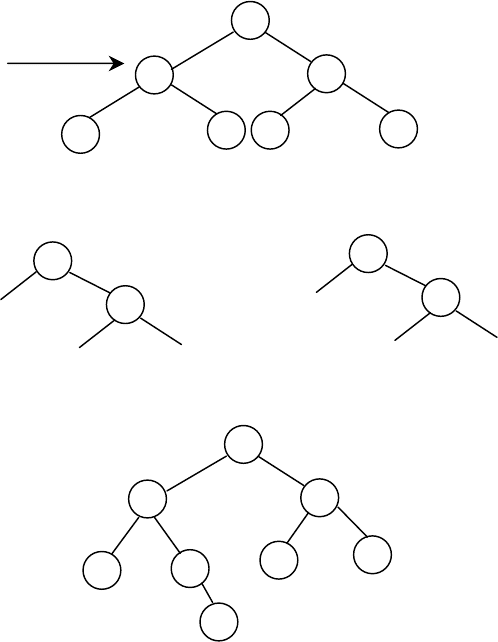
Рассмотрим добавление нового элемента на место корня на

следующем дереве.

Y = 10, X = 9

X < Y

Шаг 1 Шаг 2

Шаг 3

Рис.5.4. Добавление нового элемента на место корня

13 17

X = 9

вставить

Рассмотрим процедуру добавления нового элемента на место

корня:

add_root(empty,X,tr(X,empty,empty)). (1)

add_root(tr(Y,L,R),X,tr(X,L1,tr(Y,L2,R))):–(2)

 X<Y,

 add_root(L, X, tr(X, L1, L2)).

add_root(tr(Y,L,R),X,tr(X,tr(Y,L,R1),R2)):–(3)

 X>Y,

 add_root(R,X,tr(X,R1,R2)).

Предикат add_root содержит три объекта:

первый объект – входное дерево;

второй объект – новый элемент Х;

третий объект – выходное дерево.

Данная процедура содержит:

факт (1) – случай когда дерево пустое;

правило (2) – рекурсивное правило, новый элемент вставляется в левое

поддерево;

правило (3) – рекурсивное правило, новый элемент вставляется в правое

поддерево.

Если объединить процедуру добавления нового элемента в качестве

листа дерева и процедуру добавления на место корня, то получим

процедуру внесения нового элемента на любой уровень двоичного

упорядоченного дерева.

5.2.3. Удаление элемента из дерева

Элемент, который необходимо удалить из дерева, может

находиться в дереве в качестве листа или корня. Один из вариантов

удаления листа можно определить как операцию, обратную операции

добавления листа:

del_leaf(D1,X1,D2):–

add(D2,X,D1),

где D1 – входное дерево;

D2 – выходное дерево;

X – удаляемый элемент.

Рассмотрим случай, когда удаляемый элемент представляет какую-

нибудь внутреннюю вершину дерева.

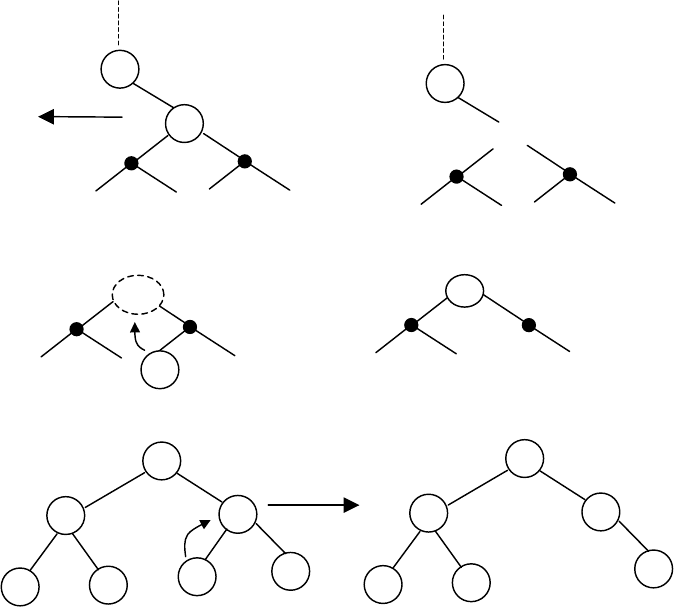
Рис.5.5. Удаление элемента из дерева. Случай удаления внутренней

вершины дерева

В данном случае при удалении элемента Х из дерева получилось

дыра. Поддеревья L и R потеряли связь с остальной частью дерева. К

вершине А оба поддерева присоединить нельзя, так как вершина А

способна принять только одно из них. Если одно из поддеревьев L и R

пустое, то непустое поддерево можно присоединить к А.

В случае, если L и R непустые поддеревья, провести такую

операцию: самую левую вершину Y правого поддерева переместить на

место удаляемой вершины Х. Упорядоченность двоичного дерева не

нарушается. Тот же будет результат, когда перемещается самая правая

Шаг

удалить

Шаг

удалить

вершина левого поддерева. Теперь рассмотрим описанный выше

алгоритм в процедуре по удалению элемента дерева с любого уровня.

del_el(tr(X, empty, R), X, R). (1)

del_el(tr(X, L, empty), X, L). (2)

del_el(tr(Х, L, R), X, tr(Y, L, R1)):– (3) 

del_min(R, Y, R1).

del_el(tr(X, L, R), Y, tr(X, L1, R)):– (4)

Y < X,

del_el(L, Y, L1). 

del_el(tr(X, L, R), Y, tr(X, L, R1)):– (5)

Y > X,

del(R, Y, R1). 

del_min(tr(Y, empty, R), Y, R). (6)

del_min(tr(X, L, R), Y, tr(X, L1, R)) :– (7)

del_min(L, Y, L1).

Предикаты del_el, del_min содержат три объекта:

первый объект – входное дерево;

второй объект – удаляемый элемент;

третий объект – выходное дерево.

Данная процедура содержит:

Факт (1), факт (2) описывают состояния, когда удаляемая вершина

Х относится к поддереву, у которого соответственно пустое левое и

правое поддерево.

Правило (3) по удалению вершины имеет подцель del_min(R, Y, R1)

по поиску самой левой вершины Y правого поддерева. Вершина Y будет

минимальной по значению в правом поддереве R. Подцель del_min(R, Y, R1)

представляет собой процедуру, состоящую из факта (6) и рекурсивного правила

(7). Факт (6) отражает случай, когда у вершины Y есть правое поддерево.

Правило (7) осуществляет поиск вершины Y.

Рекурсивные правила (4) и (5) описывают удаление элемента с уровня

листа дерева.

6. Организация баз данных

6.1. Основные понятия

В Турбо-Прологе имеются специальные средства для организации

баз данных. Они рассчитаны на реляционную модель баз данных (БД).

Реляционная модель предполагает, что БД – это описание некоторого

множества отношений. Множество фактов может определять

отношения, так же как в реляционных базах данных. Правила для

работы с БД в Турбо-Прологе могут определять сложные реляционные

вопросы, также как в реляционной алгебре. Пять основных операций

реляционной алгебры (объединение отношений, разность отношений,

декартового произведение отношений, проекция отношения, выборка

отношения) может осуществляться средствами Турбо-Пролога. В

реляционных БД информация хранится в виде прямоугольных таблиц,

на Турбо-Прологе это будет представлять собой совокупность

отношений. Описание отношений частично присутствует в явном виде

(факты) и частично в неявной форме (правила). Турбо-Пролог особенно

удобен для написания диалоговой системы именно для реляционной

БД. Внутренние унификационные подпрограммы осуществляют

автоматическую выборку фактов с нужными значениями известных

параметров и присваивают значения еще не определенным, а механизм

отката позволяет находить все имеющие ответы на сделанный запрос.

В предыдущих разделах уже рассматривались базы данных в виде

наборов фактов в разделе clauses. Механизм отката позволял осуществить

выборку всех значений объектов этих фактов. Однако необходимы более

развитые средства создания и управления базами данных. Для этого в

Турбо-Прологе существуют специальные встроенные предикаты.

Базы данных бывают статические и динамические. БД

называют статической, если ее утверждения (факты) являются частью

кода программы. Статическая БД не может быть изменена во время

работы программы. БД называется динамической, если во время работы

программы из нее можно удалять любые содержащие в ней

утверждения, а также добавлять новые. В динамической базе данных

могут содержаться только факты. Динамические БД, если имеют

небольшой объем, могут располагаться в оперативной памяти и

называются резидентными, а также располагаются на внешних

носителях.