Лазарева Т.Я., Мартемьянов Ю.Ф. и др. Теория автоматического управления
Подождите немного. Документ загружается.

5 Что такое автоколебания?
6 Изобразите фазовые портреты нелинейной системы, иллюстрирующие режимы мягкого и жесткого
возбуждения автоколебаний.
Литература: [1, 3].
Т е м а 11
УСТОЙЧИВОСТЬ И КАЧЕСТВО НЕЛИНЕЙНЫХ СИСТЕМ
Программа
Устойчивость состояния равновесия и автоколебаний в нелинейных системах. Устойчивость по А.М. Ля-
пунову. Асимптотическая устойчивость. Первый и второй методы А.М. Ляпунова.
Абсолютная устойчивость. Метод В.П. Попова. Приближенные методы исследования устойчивости и па-
раметров автоколебаний. Метод гармонического баланса.
Качество переходных процессов в нелинейных системах. Улучшение динамических свойств систем при
помощи нелинейных связей.
Методические указания
Сложные вопросы устойчивости процессов регулирования нелинейной системы можно наглядно предста-
вить, используя, как и в линейных системах, понятие фазового пространства. Здесь необходимо обратить вни-
мание на различные виды устойчивости и их геометрическую интерпретацию в фазовом пространстве. В част-
ности, необходимо знать понятия орбитальной устойчивости; устойчивости нелинейной системы "в малом", "в
большом", "в целом"; устойчивости по А.М. Ляпунову; асимптотической устойчивости.
Для исследования устойчивости нелинейных систем используются два метода А.М. Ляпунова. Первый из
них позволяет исследовать устойчивость системы "в малом", а второй – "в большом". Необходимо уметь фор-
мулировать теоремы Ляпунова, применять их к решению задач, знать основные проблемы практического ис-
пользования второго метода – это выбор функции Ляпунова. Необходимо познакомиться с рекомендации по
составлению функции Ляпунова для конкретных систем.
Для исследования абсолютной устойчивости используется метод В.П. Попова, относящийся к группе час-
тотных методов. Студенту рекомендуется познакомиться с функцией Попова, знать геометрическую интерпре-
тацию метода.
Изучение устойчивости нелинейных систем следует закончить приближенными методами исследования
устойчивости автоколебаний. Здесь необходимо отметить использование такого метода, как метод гармониче-
ского баланса, основанного на применении частотных характеристик, полученных при гармонической линеари-
зации нелинейностей.
В заключение темы студент знакомится с вопросами качества переходных процессов в нелинейных систе-
мах.
Вопросы для самопроверки
1 Как вы понимаете устойчивость состояния равновесия и устойчивость автоколебаний?
2 Дайте сравнительную характеристику различных видов устойчивости.
3 Прокомментируйте использование первого и второго методов устойчивости А.М. Ляпунова.
4 Покажите связь критерия абсолютной устойчивости Попова с критерием Найквиста.
5 Как определить устойчивость автоколебаний методом гармонического баланса?
Литература: [3, 4, 6].
Т е м а 12
СЛУЧАЙНЫЕ ПРОЦЕССЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Программа
Элементы теории вероятности. Случайные величины, законы распределения и вероятностные характери-
стики случайной величины: математическое ожидание, дисперсия, центрированная случайная величина. Поня-
тие об оценках, требования к оценкам.
Случайные стационарные процессы, свойство эргодичности, марковские процессы. Характеристики слу-
чайных процессов: корреляционная функция, спектральная плотность.
Преобразование случайных сигналов линейными системами. Характеристики выходного сигнала. Связь
между корреляционными функциями, спектральными плотностями входного и выходного сигналов.
Основные задачи анализа и синтеза систем при случайных воздействиях. Оптимальная ширина полосы
пропускания идеального полосового фильтра. Анализ и синтез систем по минимуму среднеквадратичной по-
грешности. Общая задача упреждения и фильтрации. Уравнение Винера-Хопфа и методы его решения.
Методические указания

Студентам заочного отделения тему "Случайные процессы в системах автоматического управления" реко-
мендуется изучить обзорно, познакомившись с основными понятиями, используемыми при описании случай-
ных величин, случайных стационарных процессов. Необходимо изучить и уметь составлять корреляционную
функцию и спектральную плотность случайного процесса, понять суть расчета систем автоматического управ-
ления со случайными воздействиями, знать уравнение Винера-Хопфа.
Вопросы для самопроверки
1 Назовите основные характеристики случайной величины.
2 Какой случайный процесс называется случайным стационарным процессом?
3 Что такое свойство эргодичности?
4 Как экспериментально определить корреляционную функцию случайного процесса?
5 В чем заключается расчет системы автоматического управления со случайными воздействиями?
6 Какие методы определения спектральной плотности Вам известны? Какой из них наиболее эффективен
с Вашей точки зрения?
7 Какие методы решения уравнения Винера-Хопфа Вы знаете?
Литература: [2, 3, 6].
ЗАДАНИЯ
Контрольная работа 1
Задача 1
Найти оригиналы по заданным изображениям (табл. 1).
Таблица 1
№ вари-
анта
F
1
(s) F
2
(s)
0
1
2
+
−
s
e
s
)1)(23)(1(
6
22
+++++
+
sssss
s
1
4
5
2
3
+
−
s
e
s
)55)(2(
85
22
+++
+
ssps
s
2
24
2
+
−
s
e
s
)54)(3)(2(
6
22
++++
+
sssss
s
3
16
3
2
+
−
s
e
s
)54)(2(
82
22
+++
+
sssss
s
4
3
3
2
s
e
s−
)294)(86)(4(
5
22
+++++ sssss
5
13
4
3
+
−
s
e
s
)106(
102
24
++
+
sss
s
6
3
2
5
s
e
s−
)1)(149)(1(
12
22
+++++ sssss
7
3
2
)3(
7
+
−
s
e
s
)135(
52
23
++
+
sss
s
8
2
3
2
+
−
s
e
s
)10)(46)(5(
10
22
++−++ sssss
9
4
4
s
e
s−
)1)(1(
812
23
+++
+
ssss
s
Задача 2
С помощью преобразования Лапласа решить дифференциальное уравнение с заданными начальными ус-
ловиями (табл. 2).
Таблица 2
№ вари-
Уравнение Начальные условия

анта
0 y" + 4y' + 3y = 2e
–t
cos(t) y(0) = 0; y'(0) = 1
1 y" + y' + 5y = 2sin(t) y(0) = 0; y'(0) = 0
2 y" – 2y' + 5y = 2sin(2t) y(0) = 0; y'(0) = 1
3 y" – y' + 2y = 3e
2t
cos(2t) y(0) = 0; y'(0) = 1
4
y" + 6y' + 13y =
∫
t
t
dte
0
y(0) = 0; y'(0) = 1
5 y" + y' – 5y = 2e
2t
sin(t) y(0) = 0; y'(0) = 1
6 y" + 2y' + y = e
t
y(0) = 1; y'(0) = 0
7 y
IV
– y" = e
–t
cos(t) y(0) = 0; y'(0) = –1; y"(0) = y"'(0) = 0
8 y"' – y" = e
2t
y(0) = 1 ; y'(0) = y"(0)
9 y" – y' = te
2t
y(0) = 0; y'(0) = 0
Задача 3
По известной кривой разгона и весовой функции линейного элемента (табл. 3) найти: 1) реакцию на вход-
ной сигнал
)(tx ; 2) весовую функцию или кривую разгона соответственно; 3) передаточную функцию элемента.
Таблица 3
№ варианта
)(th )(t
ω
)(tx
0
t
e
3
1
−
−
t
e
−
2
t
1
t
e
2
4
−
t
et
2−
⋅
t
2
tt +
2
t
e
−
−1
t
e
−
−1
3
t
e
2
1
−
−
t
e
2
4
−
t
e
2
1
−
−
4
te
t
+−−
−2
1
t
et
−
⋅ 1
2
−t
5
te
t
cos1
−
−
2
8
t
et
−
⋅
1
−
t
6
1
2
+t
t
e
2−
t3sin
7
2
2t
t
et
−
⋅−2 te
t
sin1
2−
−
8
)1(2
3t
e
−
−
t
et
2−
⋅ tt +
2
2
9
te
t
3sin1
2−
−
t
e
3
5
−
1
+
t
Задача 4
По известной передаточной функции элемента W(s) найти его кривую разгона, весовую функцию, ампли-
тудно-частотную, фазо-частотную, амплитудно-фазовую характеристики. Построить графики. Записать диффе-
ренциальное уравнение элемента, связывающее выходную координату и входную координату (табл. 4).
Таблица 4
№ варианта
Передаточная функ-
ция W(s)
№ варианта
Передаточная функция
W(s)
0
)2)(1(
12
++
+
ss
s
5
)12)(13(
1
++
+
ss
s
1
)2)(12(
14
++
+
ss
s
6
)34)(13(
32
++
+
ss
s
2
)3)(12(
32
++
+
ss
s
7
)34)(32(
45
+−
+
ss
s
3
)42)(23(
52
++
+
ss
s
8
)2)(12(
23
++
+
ss
s
4
)1)(43(
23
++
+
ss
s
9
)23)(12(
2
++
+
ss
s
Задача 5
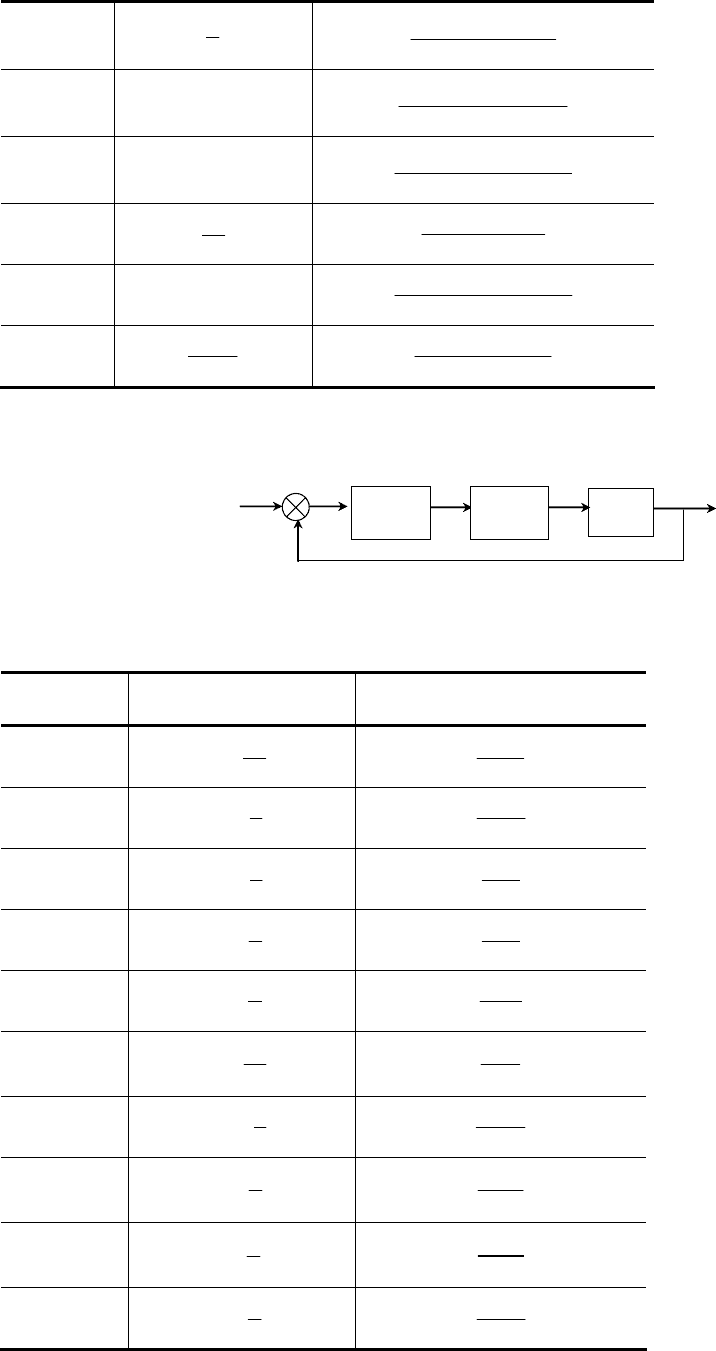
Вывести передаточную функцию для заданной структурной схемы (табл. 5).

Таблица 5
№ вари-
анта
Структурная схема
0
W
1
(s)
W
2
(s)
W
3
(s)
W
4
(s) W
6
(s)
W
5
(s)
х
y
Продолжение табл. 5
№ вари-
анта
Структурная схема
1
W
2
(s)
W
4
(s) W
5
(s)
W
3
(s)
W
1
(s)
х
y
2
W
1
(s) W
2
(s)
W
3
(s) W
4
(s)
W
6
(s)
W
5
(s)
х
y
3
W
1
(s) W
2
(s) W
5
(s)
W
3
(s)
х
y
4
х
W
1
(s)
W
2
(s)
W
3
(s)
W
4
(s)
y
5
х
W
1
(s) W
2
(s) W
3
(s)
y
Продолжение табл. 5
№ вари-
анта
Структурная схема
6

х
W
2
(s) W
3
(s)
y
W
1
(s)
W
4
(s)
W
5
(s)
7
W
3
(s)
х
W
1
(s)
W
2
(s)
W
4
(s)
y
8
W
1
(s) W
2
(s)
y
х
9
х
W
1
(s)
W
3
(s)
W
2
(s)
W
4
(s)
W
5
(s)
W
6
(s)
y
Задача 6
Исследовать на устойчивость систему автоматического регулирования, схема которой приведена на рис. 1
(табл. 6):
1) с помощью критерия Рауса–Гурвица;
2) с помощью критерия Михайлова.
W
p
(s)
x
y
W
об
(s)
Рис. 1
Таблица 6
№ варианта
W
p
(s) W
об
(s)
0
s
s34 +
123
13
23
+++
+
sss
s
1
s21+
4322
3
234
++++ ssss
2
s
s+3
13
2
23
+++ sss
3
23
+
s
2234
4
234
+++ sss
4
s
6
3233
12
23
2
+++
+
sss
s
5
2
153
5
234
2
++++
+
ssss
s
6
13 +s
522
13
234
2
++++
++
ssss
ss
7
s
2
1
42
2
23
+++
+
sss
s
8
14 +s
672
4
234
++++ ssss
9
s
s 23 +
102
32
23
+++
+
sss
s
Задача 7
Исследовать на устойчивость с помощью критерия Найквиста систему автоматического регулирования,
схема которой приведена на рис. 2 (табл. 7).
х
e
–2
s
W
p
(s) W
об
(s)
y
Рис. 2
Таблица 7
№ варианта
)(
р
sW
)(
об
sW
0
s
2
1
3 +
13
5
+
s
1
s
1
6 +
12
10
+
s
2
s
1
4 +
1
10
+
s
3
s
2
7 +
1
6
+
s
4
s
2
6 +
2
4
+
s
5
s
2
2
5 +
8
6
+s
6
s
1
10 +
32
3
+
s
7
s
2
4 +
13
2
+s
8
s
2
1+
15
4
+s
9
s
2
3 +
12
15
+
s
Контрольная работа 2
Задача 1
Уравнение статики объекта имеет вид, представленный в табл. 8. Линеаризовать уравнение в окрестности
точки
1
0
=х , )1()(
00
yхyy == . Построить статическую характеристику линеаризованного объекта и сравнить с
исходной.
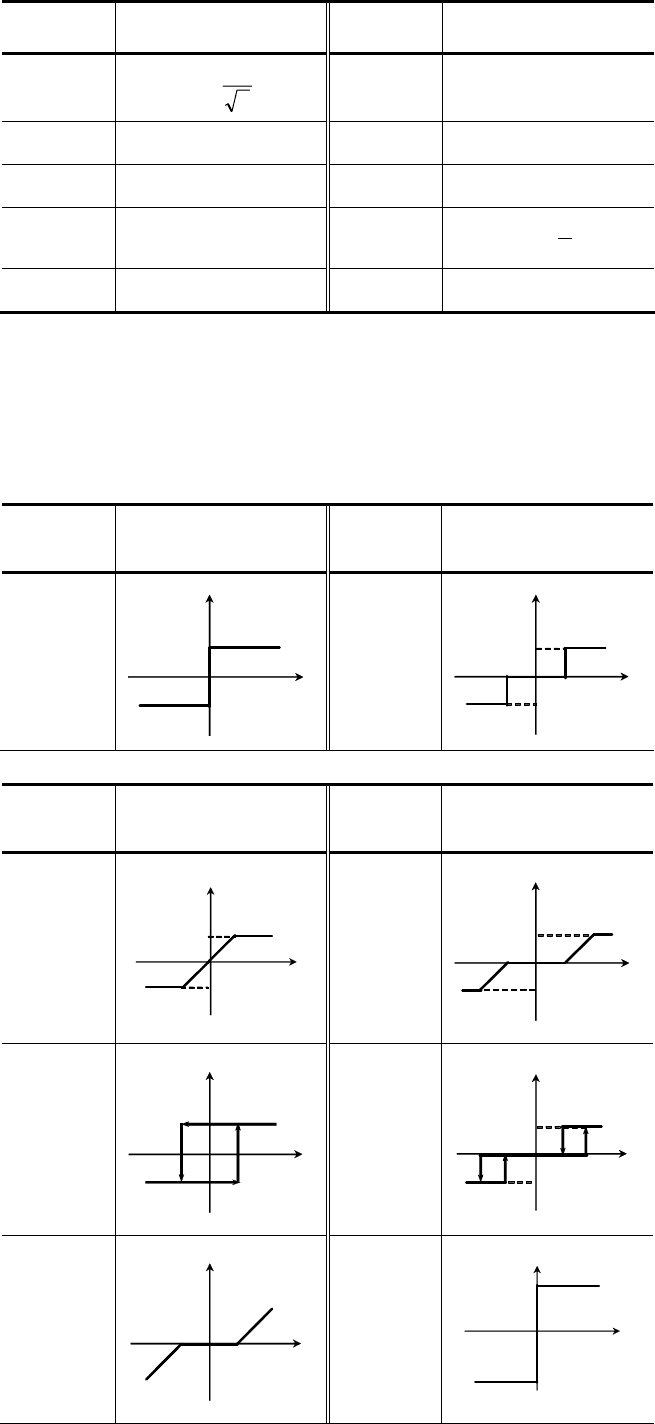
Таблица 8
№ варианта
Статическая характери-
стика
№ варианта
Статическая характери-
стика
0
х
y
1
=
1
хy =
3
2
)1ln( += хy
3
х
ey =
4
4
хy =
5
1
2
+=хy
6
5
хy =
7
х
y
1
=
8
хy =
2
9
ххy ln3
2
=
Задача 2
На вход нелинейного элемента подаются гармонические колебания. Нарисовать вынужденные колебания
на выходе нелинейного элемента. Вывести формулу эквивалентной передаточной функции нелинейного эле-
мента с помощью метода гармонической линеаризации. Статическая характеристика нелинейного элемента
приведена в табл. 9.
Таблица 9
№ варианта
Статическая характери-
стика
№ варианта
Статическая характери-
стика
0
x
y
–1
1
1
x
y
1
1
–1
–1
Продолжение табл. 9
№ варианта
Статическая характери-
стика
№ варианта
Статическая характери-
стика
2
x
y
1
–1
45°
3
x
y
1
1
–1
–1
45°
4
x
y
1
1
–1
–1
5
x
y
1
–1
–2
2
1
–1
6
x
y
1
–1
45°
7
–2
2
x
y

8
x
y
1
–1
–2
2
9
x
y
–2
2
1
–1
45°
Задача 3
Нарисовать (качественно) переходные процессы, соответствующие фазовым траекториям, указанным в
табл. 10.
Таблица 10
№ вари-
анта
Фазовая траектория
№ вари-
анта
Фазовая траектория
0
0
M
–1
y
x
1
0
M
y
x
2
0
M
y
x
3
0
M
0
M
y
x
4
1
y
x
5
0
M
0
M
y
x
6
0
M
y
x
7
0
M
y
x
8
y
x
9
y
x
0
M
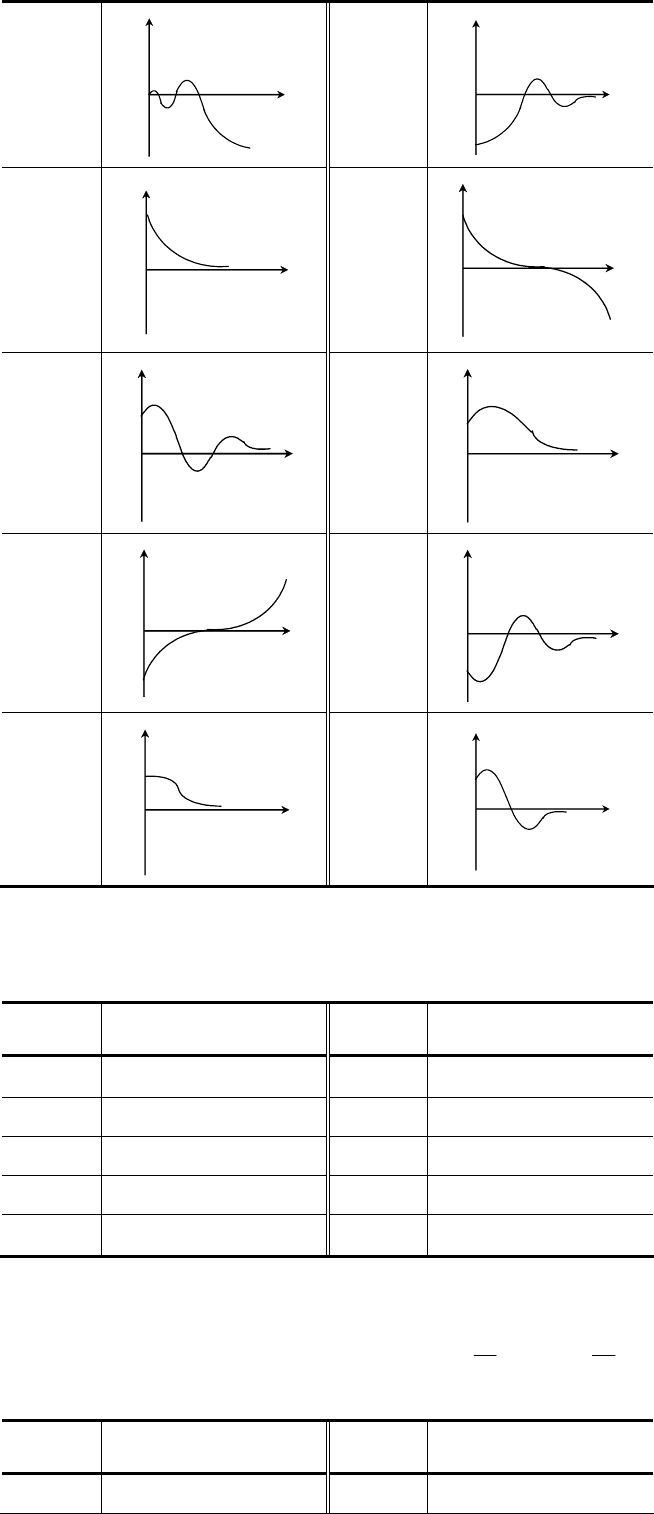
Задача 4
Нарисовать (качественно) фазовые траектории, соответствующие переходным процессам, указанным в
табл. 11.
Таблица 11
№ вари-
анта
Фазовая траектория
№ вари-
анта
Фазовая траектория
0
y
t
1
y
t
2
y
t
3
y
t
4
y
t
5
y
t
6
y
t
7
y
t
8
y
t
9
y
t
Задача 5
Построить методом изоклин фазовый портрет для системы, уравнение движения которой представлено в
табл. 12.
Таблица 12
№ вари-
анта
Уравнение
№ вари-
анта
Уравнение
0
1
2
=+
′
+
′′
хххх
1
35,0
2
=+
′
+
′′
хххх
2
1
2
=+
′
+
′′
хххх
3
1
2
=+
′
+
′′
ххххх
4
1
2
=+
′
+
′′
хххх
5
2
2
=+
′
+
′′
ххх
6
32
2
=+
′
+
′′
хххх
7
43
=
+
′
+
′
′
хххх
8
35,0
2
=++
′′
хххх
9
2
2
=+
′
+
′′
хххх
Задача 6
Определить возможные состояния равновесия системы и исследовать их устойчивость первым методом
Ляпунова, если она описывается системой уравнений:
),( yхР
dt
dх
= ; ),( yхQ
dt
dy
= (табл. 13).
Таблица 13
№ вари-
анта
Система уравнений
№ вари-
анта
Система уравнений
0
хyyyхP +−=
2
5,0),(
1
yyхP
=
),(

1),( += хyyхQ
ххyyхQ 2),(
2
+−=
2
1),( +−= хyyхP
ххyyхQ 2),(
2
+−=
3
yхyхP
+
=
),(
12),(
2
−+= yхyхQ
4
yхyхP += 5,0),(
12),(
+= хyyхQ
5
ххyyхP 2),(
2
+−=
1),(
+
=
хyyхQ
6
12),(
2
++= yхyхP
ххyyхQ 2),(
2
+−=
7
12),(
2
+= yхyхP
yхyхQ
+
=
),(
8
1),(
2
+= хyyхP
yхyхQ 5,0),( +=
9
хyyyхP 2),(
2
+−=
yхyхQ +=
2
3),(
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Контрольная работа 1
Задача 1. Найти оригиналы по заданным изображениям, используя преобразование Лапласа:
2
1
)3(
4
)(
+
=
−
s
e
sF
s
,
)136(
73
)(
23
2
++
+
=
sss
s
sF .
По таблице преобразования Лапласа и свойствам преобразования Лапласа найдем
)1(3
1
)1(4)(
−−
−=
t
tetItF ,
где
I
– единичная функция.
Для определения преобразования Лапласа от дроби
)(
2
sF необходимо эту правильную рациональную
дробь представить в виде суммы простейших дробей, которые определяются в соответствии с корнями харак-
теристического уравнения и по которым преобразование Лапласа можно взять, используя таблицы преобразо-
вания; рассматриваемая дробь имеет три нулевых корня и пару комплексно-сопряженных корней, поэтому она
разлагается на простейшие дроби следующим образом:
=
++
+
=
)136(
73
)(
23
2
sss
s
sF
=
++
+
+++
)136(
232
ss
EDs
s
C
s
B
s
A
.
)136(
)()136()136()136(
23
32222
++
++++++++++
=
sss
sEDsssCssBspssAs
В результате разложения получена сумма простейших дробей, коэффициенты которых определяются ме-
тодом неопределенных коэффициентов, для чего рассматривается равенство двух дробей. Две правильные ра-
циональные дроби равны между собой, если равны их числители и знаменатели. Так как знаменатели равны, то,
следовательно, необходимо приравнять друг к другу и числители. Приравняв в числителях коэффициенты при
одинаковых степенях параметра
s
, получим систему алгебраических уравнений для определения неизвестных
коэффициентов:
=
=+
=++
=++
=+
.713
;3613
;0613
;06
;0
C
CB
CBA
EBA
DA
Решение системы дает следующие корни:
.
2197
477
;
2197
73
;
13
7
;
169
3
;
2197
73
===−=−= EDCBA
Таким образом, исходная дробь записывается в виде
136
47773
2197
11
2197
731
169
31
13
7
)(
223
2
++
+
+−−=
ss
s
s
ss
pF
.
В соответствии с таблицами преобразований Лапласа оригинал имеет вид
.2sin
2197
129
2cos
2197
73
2197
73
169
3
26
7
)(
332
2
tetetttF
tt −−
+++−−=
Задача 2. С помощью преобразования Лапласа решить дифференциальное уравнение с заданными началь-
ными условиями:
