Lallart M. (ed.) Ferroelectrics - Physical Effects
Подождите немного. Документ загружается.


Piezoelectric Effect in Rochelle salt 5
positions. The resulting Hamiltonian is of the following form:
H
= U
0
−
∑
q,q
J
qq
2
(S
z
q1
S
z
q
1
+ S
z
q2
S
z
q
2
)+K
qq
S
z
q1
S
z
q
2
−
∑
qf
ΩS
x
qf
+(Δ
f
−2ψ
14
ε
4
+ μE
1
)S
z
qf
.
(4)
where
U
0
= N
1
2
vc
E0
44
ε
4
2
−ve
0
14
E
1
ε
4
−
1
2
vχ
ε0
11
E
2
1
.(5)
represent the elastic, piezoelectric, and electric energies attributed to a host lattice, in which
potential the pseudospin moves (with the ‘seed’ elastic constant c
E0
44
, the coefficient of
piezoelectric stress e
0
14
, and dielectric susceptibility χ
ε0
11
); v is a volume of cell, containing a pair
of pseudospins (ordering units or dipoles) of one lattice site q and different sublattices f
= 1, 2
(further we will call it a unit cell
1
), and N is a number of unit cells. The first sum describes
direct interaction of the ordering units: J
qq
= J
q
q
and K
qq
= K
q
q
are interaction potentials
between pseudospins belonging to the same and to different sublattices, respectively. The first
term in the second sum is the transverse field; the second term describes a) energy, associated
with asymmetry of the potential, where Δ
f
is asymmetry parameter: Δ
1
= −Δ
2
= Δ,b)
interaction energy of pseudospin with the field, arising due to the piezoelectric deformation
ε
4
and ψ
14
is parameter of piezoelectric coupling, c) interaction energy of pseudospin with
external electric field E
1
,whereμ is effective dipole moment of the model unit cell.
We conduct the study within the mean field approximation (MFA). Performing identical
transformation
S
z
qf
= S
z
qf
+ ΔS
z
qf
(6)
and neglecting the quadratic fluctuations, we rewrite the initial Hamiltonian (4) as
H
MFA
= U
0
+
∑
qq
J
qq
2
S
z
q1
S
z
q
1
+ S
z
q2
S
z
q
2
+ K
qq
S
z
q1
S
z
q
2
−
∑
qf
H
qf
S
qf
,(7)
where
H
qf
are the mean local fields having effect on the pseudospins S
qf
:
H
x
qf
= Ω, H
y
qf
= 0, H
z
qf
= h
qf
,
h
q1
=
∑
q
J
qq
S
z
q
1
+ K
qq
S
z
q
2
+ Δ −2ψ
14
ε
4
+ μE
1
(8a)
h
q2
=
∑
q
J
qq
S
z
q
2
+ K
qq
S
z
q
1
−Δ −2ψ
14
ε
4
+ μE
1
.(8b)
Within MFA we can calculate mean equilibrium values of the pseudospin operators:
S
qf
= Sp(S
qf
ρ
MFA
),(9)
1
Actual unit cell of the Rochelle salt crystal contains two pairs of pseudospins of two lattice sites and
different sublattices; therefore, we should set the value of the model unit cell volume to be half of the
crystal unit cell volume.
199
Piezoelectric Effect in Rochelle Salt
6 Will-be-set-by-IN-TECH
where
ρ
MFA
=
exp
−
H
MFA
k
B
T
Sp exp
−
H
MFA
k
B
T
, (10)
and k
B
is the Boltzmann constant. After calculations we derive
S
qf
=
1
2
H
qf
H
qf
tanh
H
qf
2k
B
T
, (11)
where
H
qf
≡
H
qf
= λ
qf
=
Ω
2
+ h
2
qf
.
Free energy of a crystal within MFA
F
(4)=−k
B
T ln Spexp
−
H
MFA
k
B
T
is following:
F
(4)=U
0
+
∑
qq
J
qq
2
S
z
q1
S
z
q
1
+ S
z
q2
S
z
q
2
+ K
qq
S
z
q1
S
z
q
2
−k
B
T
∑
qf
ln
2cosh
λ
qf
2k
B
T
. (12)
In homogeneous external field the system of 6N equations (11) has a lot of solutions, with a
homogeneous one among others:
S
qf
≡S
qf
0
= f (q). In case of a Rochelle salt crystal we
have J
qq
> 0, K
qq
> 0 and it is homogeneous solution which provides free energy minimum.
In this case, system of equations reduces into system
S
qf
0
=
1
2
H
(0)
f
H
(0)
f
tanh
H
(0)
f
2k
B
T
, (13)
where the local field
H
(0)
f
is following:
H
(0)x
f
= Ω, H
(0)y
f
= 0, H
(0)z
f
= h
f
,
h
1
= J
0
S
z
q1
0
+ K
0
S
z
q2
0
+ Δ −2ψ
14
ε
4
+ μE
1
, (14a)
h
2
= J
0
S
z
q2
0
+ K
0
S
z
q1
0
−Δ −2ψ
14
ε
4
+ μE
1
, (14b)
where
J
0
=
∑
q
J
qq
, K
0
=
∑
q
K
qq
; H
(0)
f
≡
H
(0)
f
= λ
f
, λ
f
=
Ω
2
+ h
2
f
.
z-component of this equation system forms two-equation system ( f
= 1, 2) to determine
S
z
qf
0
:
S
z
qf
0
=
h
f
2λ
f
tanh
λ
f
2k
B
T
. (15)
200
Ferroelectrics – Physical Effects
Piezoelectric Effect in Rochelle salt 7
Having introduced new variables
ξ
= S
q1
0
+ S
q2
0
, σ = S
q1
0
−S
q2
0
(16)
(ξ
z
and σ
z
are ferroelectric and antiferroelectric ordering parameters), we obtain system of
equations (15) in a form:
⎧
⎪
⎪
⎨
⎪
⎪
⎩
ξ
z
=
1
2
˜
h
1
˜
λ
1
tanh
˜
λ
1
2T
+
˜
h
2
˜
λ
2
tanh
˜
λ
2
2T
,
σ
z
=
1
2
˜
h
1
˜
λ
1
tanh
˜
λ
1
2T
−
˜
h
2
˜
λ
2
tanh
˜
λ
2
2T
,
(17)
where unknowns ξ
z
and σ
z
are defined at given T, E
1
, ε
4
. In system (17) the following
notations are used:
˜
h
f
= h
f
/k
B
,
˜
λ
f
=
˜
Ω
2
+
˜
h
2
f
,
˜
h
1
=
˜
R
+
0
ξ
z
+
˜
R
−
0
σ
z
+
˜
Δ
−2
˜
ψ
14
ε
4
+
˜
μE
1
,
˜
h
2
=
˜
R
+
0
ξ
z
−
˜
R
−
0
σ
z
−
˜
Δ
−2
˜
ψ
14
ε
4
+
˜
μE
1
.
(18)
Here
˜
Ω
=
Ω
k
B
,
˜
Δ =
Δ
k
B
,
˜
ψ
14
=
ψ
14
k
B
,
˜
μ =
μ
k
B
,
˜
R
±
0
=
˜
J
0
±
˜
K
0
2
,
˜
J
0
=
J
0
k
B
,
˜
K
0
=
K
0
k
B
. (19)
The system (17) is system of two equations with unknowns ξ
z
and σ
z
.
When values ξ
z
and σ
z
are defined, we can calculate values ξ
x
and σ
x
using (13) and (16):
ξ
x
=
1
2
˜
Ω
˜
λ
1
tanh
˜
λ
1
2T
+
˜
Ω
˜
λ
2
tanh
˜
λ
2
2T
, σ
x
=
1
2
˜
Ω
˜
λ
1
tanh
˜
λ
1
2T
−
˜
Ω
˜
λ
2
tanh
˜
λ
2
2T
;
values ξ
y
, σ
y
are equal to zero.
Free energy per model unit cell f
(4)=F(4)/( k
B
N) in variables ξ
z
and σ
z
is following:
f
(4)=
˜
v
2
c
E0
44
ε
4
2
−
˜
ve
0
14
ε
4
E
1
−
˜
v
2
χ
ε0
11
E
1
2
+
˜
R
+
0
2
(ξ
z
)
2
+
˜
R
−
0
2
(σ
z
)
2
− T
∑
f
ln
2cosh
˜
λ
f
2T
, (20)
where
˜
v
=
v
k
B
. By differentiating free energy we can find dielectric, elastic, and piezoelectric
properties of the Rochelle salt.
The conditions
1
˜
v
∂ f
(4)
∂ε
4
E
1
,T
= σ
4
,
1
˜
v
∂ f
(4)
∂E
1
ε
4
,T
= −P
1
yield the following expression for stress σ
4
and polarization P
1
:
σ
4
= c
E0
44
ε
4
−e
0
14
E
1
+
2
˜
ψ
14
˜
v
ξ
z
, (21a)
P
1
= e
0
14
ε
4
+ χ
ε0
11
E
1
+
˜
μ
˜
v
ξ
z
. (21b)
201
Piezoelectric Effect in Rochelle Salt

8 Will-be-set-by-IN-TECH
Independent variable is stress rather than deformation, so we need express local fields in
terms of σ
4
when solving system (17). Having used (21a) we derive
ε
4
=
σ
4
c
E0
44
+
e
0
14
c
E0
44
E
1
−
2
˜
ψ
14
˜
vc
E0
44
ξ
z
. (22)
On the basis of Eq. (22) we can rewrite local fields in the following way:
˜
h
1
=
˜
R
+
0
ξ
z
+
˜
R
−
0
σ
z
+
˜
Δ
−
2
˜
ψ
14
c
E0
44
σ
4
+
˜
μ
E
1
, (23a)
˜
h
2
=
˜
R
+
0
ξ
z
−
˜
R
−
0
σ
z
−
˜
Δ
−
2
˜
ψ
14
c
E0
44
σ
4
+
˜
μ
E
1
, (23b)
where
˜
R
+
and
˜
μ
are following:
˜
R
+
0
=
˜
R
+
0
+
4
˜
ψ
2
14
˜
vc
E0
44
,
˜
μ
=
˜
μ
−
2
˜
ψ
14
e
0
14
c
E0
44
. (24)
System (17) with local fields (23), considered at σ
4
= 0, E
1
= 0, has solutions of two types:
ξ
z
= 0andξ
z
= 0. The minimum Helmholtz free energy (g(4)= f (4) −
˜
vσ
4
ε
4
) condition
defines which of the solutions is actually realized at each particular T. The solution of first
type describes paraelectric phase and the solution of second type describes ferroelectric phase.
In paraelectric phase we have also σ
x
= 0.
We will calculate elastic, piezoelectric, and dielectric constants by differentiation P
1
(21b) and
σ
4
(21a) at constant T:
d P
1
= e
14
d ε
4
+ χ
ε
11
d E
1
, (25a)
d σ
4
= c
E
44
d ε
4
−e
14
d E
1
. (25b)
Here χ
ε
11
is longitudinal dielectric susceptibility at constant strain, c
E
44
is elastic constant at
constant field, e
14
is coefficient of the piezoelectric stress.
The result is following:
2
χ
ε
11
=
∂P
1
∂E
1
ε
4
= χ
ε0
11
+
˜
μ
˜
v
∂ξ
z
∂E
1
ε
4
= χ
ε0
11
+
˜
μ
2
˜
v
f
1
(T, σ
4
, E
1
), (26)
where
f
1
(T, σ
4
, E
1
)=
e
1
−
˜
R
−
0
(e
1
2
−e
2
2
)
1 −e
1
(
˜
R
+
0
+
˜
R
−
0
)+
˜
R
+
0
˜
R
−
0
(e
1
2
−e
2
2
)
(27)
and following notations are used:
e
1
=
a
1
+ a
2
4T
+
˜
Ω
2
(b
1
+ b
2
)
2
, e
2
=
a
1
− a
2
4T
+
˜
Ω
2
(b
1
−b
2
)
2
,
a
i
=
˜
h
2
i
˜
λ
2
i
−η
i
2
, b
i
=
η
i
˜
h
i
˜
λ
2
i
, (i = 1, 2); η
1
= ξ
z
+ σ
z
, η
2
= ξ
z
−σ
z
.
(28)
2
All partial derivatives of ξ
z
were derived by differentiating Eq. (17).
202
Ferroelectrics – Physical Effects

Piezoelectric Effect in Rochelle salt 9
Coefficient of the piezoelectric stress:
e
14
=
∂P
1
∂ε
4
E
1
= e
0
14
−
2
˜
μ
˜
ψ
14
˜
v
f
1
(T, σ
4
, E
1
). (29)
Elastic constant at constant field:
c
E
44
=
∂σ
4
∂ε
4
E
1
= c
E0
44
−
4
˜
ψ
2
14
˜
v
f
1
(T, σ
4
, E
1
). (30)
Coefficient of the piezoelectric strain d
14
=(∂P
1
/∂σ
4
)
E
1
and dielectric susceptibility of free
crystal χ
σ
11
=(∂P
1
/∂E
1
)
σ
4
could be derived through e
14
, c
E
44
and χ
ε
11
:
d
14
=
e
14
c
E
44
, χ
σ
11
= χ
ε
11
+ e
14
d
14
.
We may notice that at
˜
Ω
= 0 all results presented here coincide with the results of previous
calculations (Levitskii et al., 2003), where transverse field was not taken into account.
3.2 Results of calculations for Rochelle salt
The proposed model was used for analysis of physical properties of Rochelle salt crystal that is
not externally affected (E
1
= 0, σ
4
= 0). To obtain specific numerical results it is necessary first
of all to derive theory model parameters for calculations. Deriving procedure was described
in (Levitskii, Zachek & Andrusyk, 2010) and here we will restrict ourselves to parameters
presenting:
˜
Ω
= 113.467 K,
˜
J
0
= 813.216 K,
˜
K
0
= 1447.17 K,
˜
Δ = 719.937 K,
˜
ψ
4
= −720.0 K,
c
E0
44
= 1.224 ×10
10
Nm
−2
, e
0
14
= 31.64 ×10
−2
Cm
−2
, χ
ε0
11
= 0.0,
μ
(T)=a + k(T −297), a = 8.157 ×10
−30
Cm, k = −0.0185 ×10
−30
CmK
−1
.
(31)
Unit cell volume (volume per two pseudospins from the same site and different sublattices) is
v
= 5.219 ×10
−22
cm
3
(Bronowska, 1981).
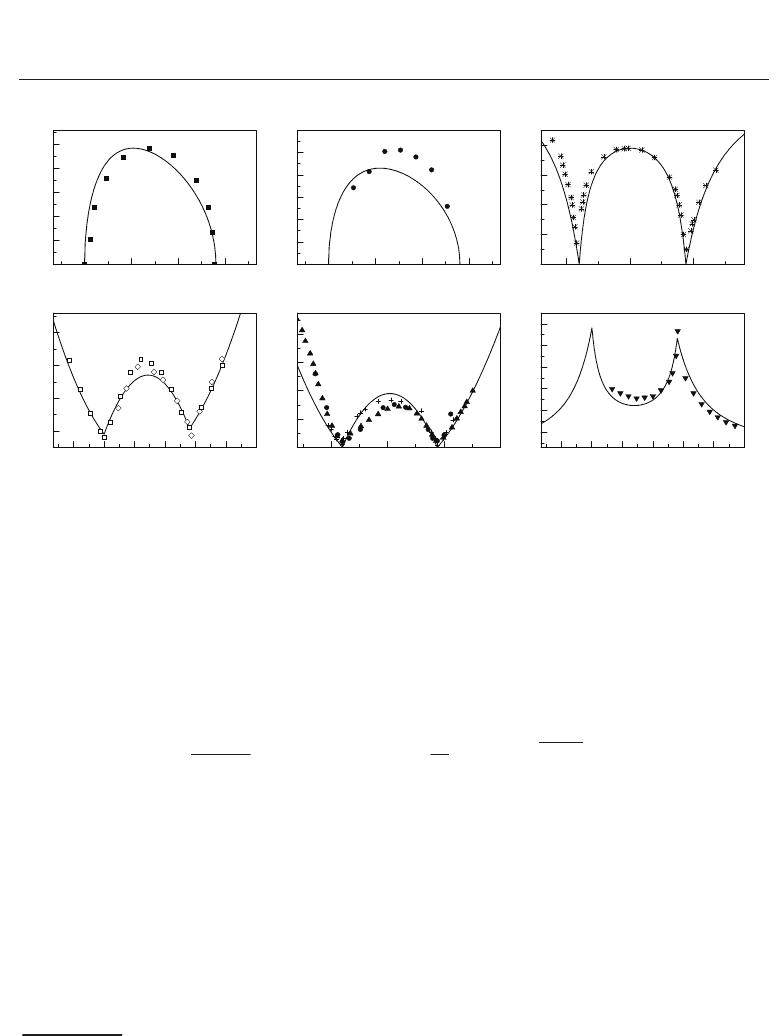
The results of calculations made for static dielectric characteristics are shown together with
experimental data in Fig. 4. The derived agreement is very good considering that Mitsui
model is rather inaccurate model of RS and the used MFA is a weak approximation.
Besides, we derived that dielectric permittivity of the free crystal has singularity in the
transition points while dielectric permittivity of the clamped crystal doesn’t. Elastic constant
c
44
becomes equal to zero at the transition points, coefficient of the piezoelectric stress e
14
doesn’t have singularity in the transition point. All these results agree with the prediction of
the Landau theory for the behaviour of physical characteristics in the vicinity of the transition
points. However, presented semimicroscopic approach has an advantage over the Landau
theory: it allowed to explain physical properties of Rochelle salt in wide temperature rage
containing both transition points in natural way. Besides that Mitsui model gives some insight
into microscopical mechanism of the phase transition of Rochelle salt.
203
Piezoelectric Effect in Rochelle Salt
10 Will-be-set-by-IN-TECH
240 255 270 285 300 315
1
2
3
4
5
6
240 255 270 285 300 315
0,05
0,10
0,15
0,20
255 270 285 300
0,0
0,5
1,0
1,5
2,0
2,5
e
14
(Cm
-2
)
T (K)
1/
χ
ε
11
T (K)
250 275 300
0,00
0,04
0,08
0,12
0,16
1/
χ
σ
11
T (K)
250 275 300
0
2
4
6
8
c
44
E
(10
9
Nm
-2
)
T (K)
P
1
(10
-3
Cm
-2
)
ε
4
(10
-4
)
T (K)
255 270 285 300
0
1
2
3
4
5
6
T (K)
Fig. 4. Theoretical and experimental physical characteristics of Rochelle salt. Solid line
corresponds to calculations, Points are the experimental data. P
1
(T): (Cady, 1964), ε
4
(T): •
(Ubbelohde & Woodward, 1946), c
E
44
: ∗ (Yu. Serdobolskaya, 1996), 1/χ
ε
11
(T): (Sandy &
Jones, 1968),
♦ (Mueller, 1935), 1/χ
σ
11
(T): (Taylor et al., 1984), e
14
(T): (Beige & Kühnel,
1984).
4. Dynamic properties of Rochelle salt
4.1 Order parameter dynamics. Dielectric susceptibility of a clamped crystal
We consider dynamic properties of the system with Hamiltonian (4) within the Bloch
equations method
¯h
d
S
qf
t
dt
= S
qf
t
×H
qf
(t) −
¯h
T
1
S
qf
t
−S
qf
t
. (32)
Right part of this equation consists of two terms.
The first term is Heisenberg part of the motion equation, calculated within random phase
approximation (RPA), where ‘
×’ denotes the vector product and H
qf
(t) are the instantaneous
values of the local fields:
3
H
x
qf
(t)=Ω, H
y
qf
= 0, H
z
qf
(t)=h
qf
(t), (33)
3
Original Heisenberg part of the motion equation is −
i
[S
qf
, H ]
t
. Within RPA mean value of
commutator with time dependent statistical operator in form of (10) is to be calculated. Doing necessary
calculations one can derive that
−i[S
qf
, H ]
t
= S
qf
t
×H
qf
( t).
204
Ferroelectrics – Physical Effects

Piezoelectric Effect in Rochelle salt 11
h
q1
(t)=
∑
q
J
qq
S
z
q
1
t
+ K
qq
S
z
q
2
t
+ Δ −2ψ
14
ε
4q
(t)+μE
1q
(t), (34a)
h
q2
(t)=
∑
q
J
qq
S
z
q
2
t
+ K
qq
S
z
q
1
t
−Δ −2ψ
14
ε
4q
(t)+μE
1q
(t). (34b)
The second term describes relaxation of the pseudospin component
S
qf
t
(longitudinal
to the instantaneous value of the local field) towards its quasiequilibrium value with a
characteristic time T
1
.
4
Quasiequilibrium mean values S
qf
t
aredefinedas(seeEq.(11)):
S
qf
t
=
1
2
H
qf
(t)
H
qf
(t)
tanh
1
2k
B
T
H
qf
(t)
. (35)
Relaxation term describes non-equilibrium processes in a pseudospin system. In real
situation, a pseudospin system is not an isolated system, whereas it is a part of a larger system.
That part of extended system which is not a pseudospin subsystem appears as thermostat that
behaves without criticality. Respectively, pseudospin excitations relax due to the interaction
with thermostat to their quasiequilibrium values for a characteristic relaxation time T
1
.As
far as a phase transition is a collective effect and the relaxation term in Eq. (32) describes
individual relaxation of each pseudospin, it becomes clear that relaxation time T
1
should have
no singularity at the Curie point. Relaxation time can be derived ab initio butweconsideritto
be a model parameter and take it to be independent from temperature.
In the same way it can be explained why relaxation in Eq. (32) occurs towards
quasiequilibrium state and not to thermodynamic equilibrium state. Relaxation term
describes individual relaxation of pseudospin, which ‘is not aware’ of the state of
thermodynamic equilibrium but ‘is aware’ of the state of its environment at a particular
moment. At every moment this environment creates instantaneous molecular fields which
define quasiequilibrium state. Instantaneous quasiequilibrium average of pseudospin
operators are defined from Eq. (9), (10) but with molecular fields Eq. (33), (34). Making
necessary calculations we obtain quasiequilibrium average
S
qf
t
in form of Eq. (35).
Eventually, of course, quasiequilibrium values follow to equilibrium ones and relaxation leads
excited system to thermodynamic equilibrium state.
As we are interested in linear response of the system to a small external variable electric field
δE
1q
(t)
E
1q
(t)=E
1
+ δE
1q
(t)
,
it is sufficiently to present
S
qf
t
as a sum of constant term S
qf
0
(mean equilibrium value,
calculated in MFA) and time dependent small deviation δ
S
qf
t
:
S
qf
t
= S
qf
0
+ δS
qf
t
. (36)
4
Sometimes one writes third term −
¯h
T
2
S
qf
t⊥
, describing decay process of the transverse component of
pseudospin
S
qf
t⊥
, though it can be shown (Levitskii, Andrusyk & Zachek, 2010) that its impact on
Rochelle salt dynamics is negligible.
205
Piezoelectric Effect in Rochelle Salt

12 Will-be-set-by-IN-TECH
Similarly:
H
qf
(t)=H
(0)
f
+ δH
qf
(t), S
qf
t
= S
qf
0
+ δS
qf
t
. (37)
Now, we can linearize motion equation (32) by retaining terms, which are linear in deviations
δ
S
qf
t
, δH
qf
(t), δS
qf
t
:
¯h
dδ
S
qf
t
dt
= δS
qf
t
×H
(0)
f
+ S
qf
0
×δH
qf
(t) −
¯h
T
1
δ
S
qf
t
−δS
qf
t
, (38)
where
δ
H
x
qf
(t)=0, δH
y
qf
(t)=0,
δ
H
z
q1
(t)=
∑
q
J
qq
δS
z
q
1
t
+
∑
q
K
qq
δS
z
q
2
t
−2ψ
14
δε
4q
(t)+μδE
1q
(t),
δ
H
z
q2
(t)=
∑
q
K
qq
δS
z
q
1
t
+
∑
q
J
qq
δS
z
q
2
t
−2ψ
14
δε
4q
(t)+μδE
1q
(t).
Now, we transform equation (38) into a form involving single variable δ
S
qf
t
,thenFourier
transform into the frequency domain and Fourier transform to k-space,
5
introduce new theory
parameters
˜
R
+
k
=
˜
J
k
+
˜
K
k
2
,
˜
R
−
k
=
˜
J
k
−
˜
K
k
2
(
˜
J
k
= J
k
/k
B
,
˜
K
k
= K
k
/k
B
), (39)
and introduce new variables δξ
k
(t), δσ
k
(t)
δS
k1
t
=
δξ
k
(t)+δσ
k
(t)
2
, δ
S
k2
t
=
δξ
k
(t) − δσ
k
(t)
2
. (40)
Upon application of these transformations, the Bloch equation (38) reduces to system of linear
differential equations of the following matrix form:
A
k
−i
¯h
k
B
ω · I
δx
k
(ω)=(
˜
μδE
1k
(ω) −2
˜
ψ
14
δε
4k
(ω))b. (41)
5
Fourier transform to k-space is
A
q
=
∑
k
a
k
exp (
i
kq
), a
k
=
1
N
∑
q
A
q
exp (−
i
kq
)
for values dependent on q (like δS
z
q1
t
and others) and
M
q
1
q
2
=
1
N
∑
k
m
k
exp (
i
k
( q
1
−q
2
)), m
k
=
∑
q
2
M
q
1
q
2
exp (−
i
k
( q
1
− q
2
)).
for interaction constants dependent on q
1
and q
2
(like J
qq
and others). Here the dependency of M
q
1
q
2
on difference q
1
−q
2
was used.
206
Ferroelectrics – Physical Effects

Piezoelectric Effect in Rochelle salt 13
The following notations are used in this equation: I is identity matrix, i is the imaginary unit,
A
k
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
a
11
a
12
−
˜
Ω 0 a
15
a
16
a
21
a
22
0 −
˜
Ω a
16
a
15
a
31
a
32
00a
35
a
36
a
41
a
42
00a
36
a
35
a
51
a
52
−a
35
−a
36
a
55
a
56
a
61
a
62
−a
36
−a
35
a
56
a
55
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
, δx
k
(ω)=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
δξ
z
k
(ω)
δσ
z
k
(ω)
δξ
y
k
(ω)
δσ
y
k
(ω)
δξ
x
k
(ω)
δσ
x
k
(ω)
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
, b
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
b
1
b
2
ξ
x
σ
x
b
5
b
6
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
. (42)
Matrix A
k
components:
a
11
= U
1
+
˜
R
+
k
G
1
, a
12
= U
2
+
˜
R
−
k
G
2
, a
15
= V
1
, a
16
= V
2
,
a
21
= U
2
+
˜
R
+
k
G
2
, a
22
= U
1
+
˜
R
−
k
G
1
,
a
31
=
˜
Ω
−
˜
R
+
k
ξ
x
, a
32
= −
˜
R
−
k
σ
x
, a
35
= −
˜
R
+
0
ξ
z
−2
˜
ψ
14
ε
4
, a
36
= −
˜
R
−
0
σ
z
+
˜
Δ
,
a
41
= −
˜
R
+
k
σ
x
, a
42
=
˜
Ω
−
˜
R
−
k
ξ
x
,
a
51
= V
1
+
˜
R
+
k
H
1
, a
52
= V
2
+
˜
R
−
k
H
2
, a
55
= W
1
, a
56
= W
2
,
a
61
= V
2
+
˜
R
+
k
H
2
, a
62
= V
1
+
˜
R
−
k
H
1
;
(43)
components of vector b:
b
1
= −G
1
, b
2
= −G
2
, b
5
= −H
1
, b
6
= −H
2
, (44)
where following notations were used
U
1,2
= −
1
2T
1
˜
ε
2
1
˜
λ
2
1
±
˜
ε
2
2
˜
λ
2
2
, V
1,2
= −
1
2T
1
˜
Ω
˜
ε
1
˜
λ
2
1
±
˜
Ω
˜
ε
2
˜
λ
2
2
, G
1,2
= K
1
˜
ε
2
1
˜
λ
2
1
±K
2
˜
ε
2
2
˜
λ
2
2
,
W
1,2
= −
1
2T
1
˜
Ω
2
˜
λ
2
1
±
˜
Ω
2
˜
λ
2
2
, H
1,2
= K
1
˜
Ω
˜
ε
1
˜
λ
2
1
±K
2
˜
Ω
˜
ε
2
˜
λ
2
2
, K
1,2
=
1
T
1
1
4T cosh
2
˜
λ
1,2
2T
,
and relaxation time T
1
is
T
1
=
k
B
¯h
T
1
. (45)
It is convenient to present the solution of Eq. (41) in a form
δx
k
(ω)=(
˜
μδE
1k
(ω) −2
˜
ψ
14
δε
4k
(ω))
A
k
−i
¯h
k
B
ω · I
−1
b
, (46)
where we denote the inverse of matrix
A
k
−i
¯h
k
B
ω · I
by
A
k
−i
¯h
k
B
ω · I
−1
.
Now it is useful to present all variables in Eq. (21b) as a sum of constant (equilibrium) term
and small variation term. The result for δP
1k
(ω) is
δP
1k
(ω)=e
0
14
δε
4k
(ω)+χ
ε0
11
·δE
1k
(ω)+
˜
μ
˜
v
·δξ
z
k
(ω). (47)
207
Piezoelectric Effect in Rochelle Salt
14 Will-be-set-by-IN-TECH
If to note that δξ
z
k
(ω) is the first component of vector δx
k
(ω), variation of polarization can be
presented as
δP
1k
(ω)=e
14
(k, ω)δε
4k
(ω)+χ
ε
11
(k, ω)δE
1k
(ω). (48)
Here χ
ε
11
(k, ω) is dynamic susceptibility of a clamped crystal (δε
4k
(ω)=0), and e
14
(k, ω) is
dynamic coefficient of the piezoelectric stress:
χ
ε
11
(k, ω)=χ
ε0
11
+
˜
μ
2
˜
v
F
1
(k,iω) , e
14
(k, ω)=e
0
14
−
2
˜
ψ
14
˜
μ
˜
v
F
1
(k,iω). (49)
The following notation was used:
F
1
(k,iω)=
A
k
−i
¯h
k
B
ω · I
−1
b
1
, (50)
where subscript ‘1’ denotes the first component of the vector derived by multiplication of
matrix
A
k
−i
¯h
k
B
ω · I
−1
and vector b.
Analysis shows that F
1
(0,0)=f
1
(T, σ
4
, E
1
) at any relaxation times T
1
. Therefore, all dynamic
physical characteristics are equal to correspondent static characteristics at ω
= 0.
The best agreement between theory and experiment for RS is reached at (Levitskii, Andrusyk
& Zachek, 2010)
T
1
= 1.767 ×10
−13
s (T
1
= 2.313 ×10
−2
K). (51)
It is easily seen that the function F
1
(k,iω) is a rational function of iω, where numerator is
polynomial function of degree not higher than 5 and denominator is polynomial function of
degree 6. Therefore, we can decompose function F
1
(k,iω) into partial fractions:
F
1
(k,iω)=
n
∑
i=1
k
i
τ
i
1 + iωτ
i
+
m
∑
j=1
M
j
(iω)+N
j
(iω)
2
+ p
j
(iω)+q
j
. (52)
Here coefficients k
i
, τ
i
, M
j
, N
j
, p
j
, q
j
are real numbers, n is number of real (equal to −1/τ
i
)
eigen values and 2m is number of complex eigen values of matrix A
k
.Valuesn and 2m
are defined by theory parameters and temperature. However, matrix A
k
has 6 eigen values
in total. The first sum in Eq. (52) is a contribution of Debye (relaxation) modes into order
parameter dynamics, and the second sum is a contribution of resonance modes. In RS case we
have n
= 2, m = 2 at all temperatures.
The results of calculations performed in the center of the Brillouin zone (k
= 0) are presented
below. Fig. 5 presents frequency dependencies of dielectric permittivity of clamped crystal in
dispersion region (10
9
Hz – 10
11
Hz) calculated theoretically along with experimental data. As
figure shows, Mitsui model is able to describe dielectric permittivity in dispersion region.
The correspondence between theory and experimental data for dynamic dielectric
permittivity deserves special attention. Methods for experimental measurements of dynamic
dielectric permittivity does not allow to assert that namely clamped crystal permittivity was
208
Ferroelectrics – Physical Effects
