Лабораторные работы по курсу общей физики (2-я Редакция 2012 г.)
Подождите немного. Документ загружается.


∫
∫
∞
∞
=
′
=
0
0
),(
),(),(
ωω
ωωω
dTf
dTfTa
R
R
a
e
e
T
(6)
Из формул (3) и (6) следует, что
4
TaRaR
TeTe
σ==
′
(7)
Если поглощающая способность тела
)
,
(
T
a
ω
не зависит от частоты, т. е.
)
(
)
,
(
T
a
T
a
=
ω
, то такое тело называют серым. В этом случае в выражении (6)
)
(
T
a
можно вынести за знак интеграла. В результате получим равенство
)(Taa
T
=
, т. е. степень черноты серого тела совпадает с его поглощательной
способностью.
Мощность, излучаемая телом, пропорциональна энергетической
светимости:
STaSRP
Te
4
σ=
′
= , (8)
где
S
- площадь излучающей поверхности. Если в интересующем нас интервале
температур степень черноты тела
T
a от температуры зависит слабо, то
приближенно можно считать ее постоянной величиной, равной среднему
значению в этом интервале. Выражение (8) в этом случае можно разрешить
относительно температуры
T
. Тогда
4
1
4
1
)(
−−
= PSaT
T
σ . (9)
Полученное выражение для T подставим в формулу (2). Получим
).exp(
4
1
4
1
4
1
4
1
−
−∝ PSa
k
I
T
σ
ω
h
(10)
Излучение в узком диапазоне частот
ω
d
вблизи частоты
ω
, интенсивность
которого описывается формулой (10), попадает на фотоприемник, показания
которого пропорциональны интенсивности падающего на него излучения. При
этом
)exp(
4
1
4
1
4
1
4
1
−
−= PSa
k
CU
TФ
σ
ω
h
, (11)
где
Ф
U - показания фотоприемника, C – коэффициент пропорциональности.
Прологарифмируем выражение (11). Тогда
4
1
4
1
4
1
4
1
lnln
−
−= PSa
k
CU
TФ
σ
ω
h
. (12)
Из выражения (12) следует, что график зависимости
Ф
Uln от
4
1
−
P
имеет вид
прямой линии, причем тангенс угла наклона этой прямой
4
1
)( Sa
k
tg
T
σ
ω
ϕ
h
= . (13)
Вид такого графика показан на рисунке 1.
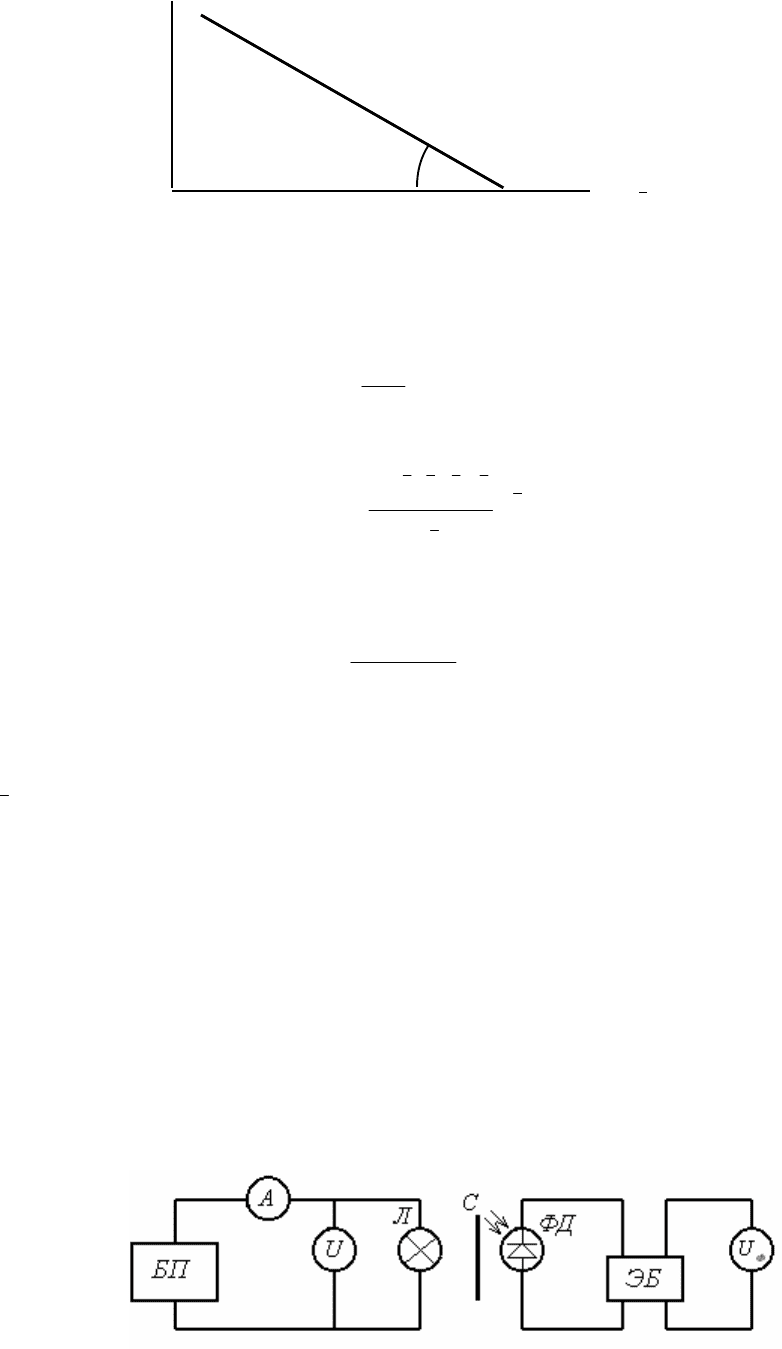
ln
Ф
U
ϕ
4
1
P
−
Рис. 1
Подставив в формулу (13) значение
σ
из формулы (4) и используя известное
соотношение
λ
π
ω
c2
= ,
где с – скорость света,
λ
- длина волны, получим
4
1
4
1
4
1
4
1
2
1
2
3
60
2
h
λ
π
ϕ
Sac
tg
T
= (14)
Из выражения (14) следует, что
ϕ
π
λ
4
26
4
4
15
tg
Sac
T
=h (15)
Постоянную Планка
h
можно определить по формуле (15), если на основании
экспериментально полученных данных построить график зависимости
Ф
Uln от
4
1
−
P
и найти из него
ϕ
tg
.
Мощность излучения
P
можно считать равной подводимой мощности. В
настоящей работе она выделяется за счет протекания по нагреваемому телу
электрического тока. Поэтому мощность можно определить по формуле
IU
P
=
(16)
где I – сила тока, U – напряжение.
Описание экспериментальной установки
Измерение величин, необходимых для построения графика , производятся
на установке, схема которой показана на рисунке 2.
Рис. 2
На этом рисунке БП – блок питания, А – амперметр, U – вольтметр, Л – лампочка
накаливания, С – светофильтр, ФД – фотодиод, ЭБ – электронный блок

фотоприемника,
Ф
U - вольтметр, регистрирующий напряжение на выходе
электронного блока.
Длина волны
λ
, регистрируемая установкой равна 1 мкм. Значения
площади излучающей поверхности лампочки S и поглощательной способности
T
a даны в паспорте установки.
Задание к работе
1. Измерить ряд значений величин, необходимых для построения графика.
2. Построить график зависимости
Ф
Uln от
4
1
−
P
.
3. ПО графику определить
ϕ
tg
.
4. По формуле (15) оценить величину постоянной Планка
h
.
5. Полученное значение
h
сравнить с табличным.
Контрольные вопросы
1. Какова цель работы?
2. Что такое испускательная способность?
3. Что такое поглощательная способность?
4. Что такое энергетическая светимость?
5. Напишите формулу Планка для испускательной способности черного тела.
6. Сформулируйте закон Стефана – Больцмана.
7. Какие факторы могут привести к погрешности в определении постоянной
Планка?
Литература
1. Савельев И.В. Курс общей физики. – М.: Наука, 1989. – Т.3. - § 1, 5.
2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1990. - § 197, 200.







