Лабораторная работа - Метод последовательных приближений
Подождите немного. Документ загружается.


2
ВВЕДЕНИЕ
Целью лабораторной работы является написание программы которая решала
бы уравнение методом последовательных приближений.
1ТЕОРЕТИЧЕСКИЕ ИССЛЕДОВАНИЯ
1.1. Метод последовательных приближений
1.1.1. Описание метода
Нахождение корней уравнения – это одна из древнейших математических задач,
которая не потеряла актуальности и в наши дни: она часта встречается в самых
разнообразных областях науки и техники. В общем случае, если имеется некоторая
функция
F( x )
, то бывает необходимо найти такие значения аргумента
x
, для
которых
F( x )=0
(1.1)
Функция
F( x )
может быть алгебраической или трансцендентной.
Предполагается обычно, что она дифференцируема, т.е. не имеет точек разрыва.
В этом разделе будут рассмотрены функции, которые не имеют аналитических
формул для нахождения корней.
Предположим, что (1.1) переписано в виде
x=f ( x ).
(1.2)
Это преобразование можно получить, если в левую и правую части уравнения
(1.1)добавить
x
, т.е.
f (x )=F (x )+x .
(1.3)
Пусть
x
0
будет исходным приближением уравнения (1.2), тогда в качестве
следующего приближения примем
x
1
=f ( x
0
).

3
В качестве следующего приближения возьмём
x
2
=f ( x
1
).
Продолжая этот процесс, в качестве
n
-го приближения необходимо положить
x
n
=f ( x
n
−1).
(1.4)
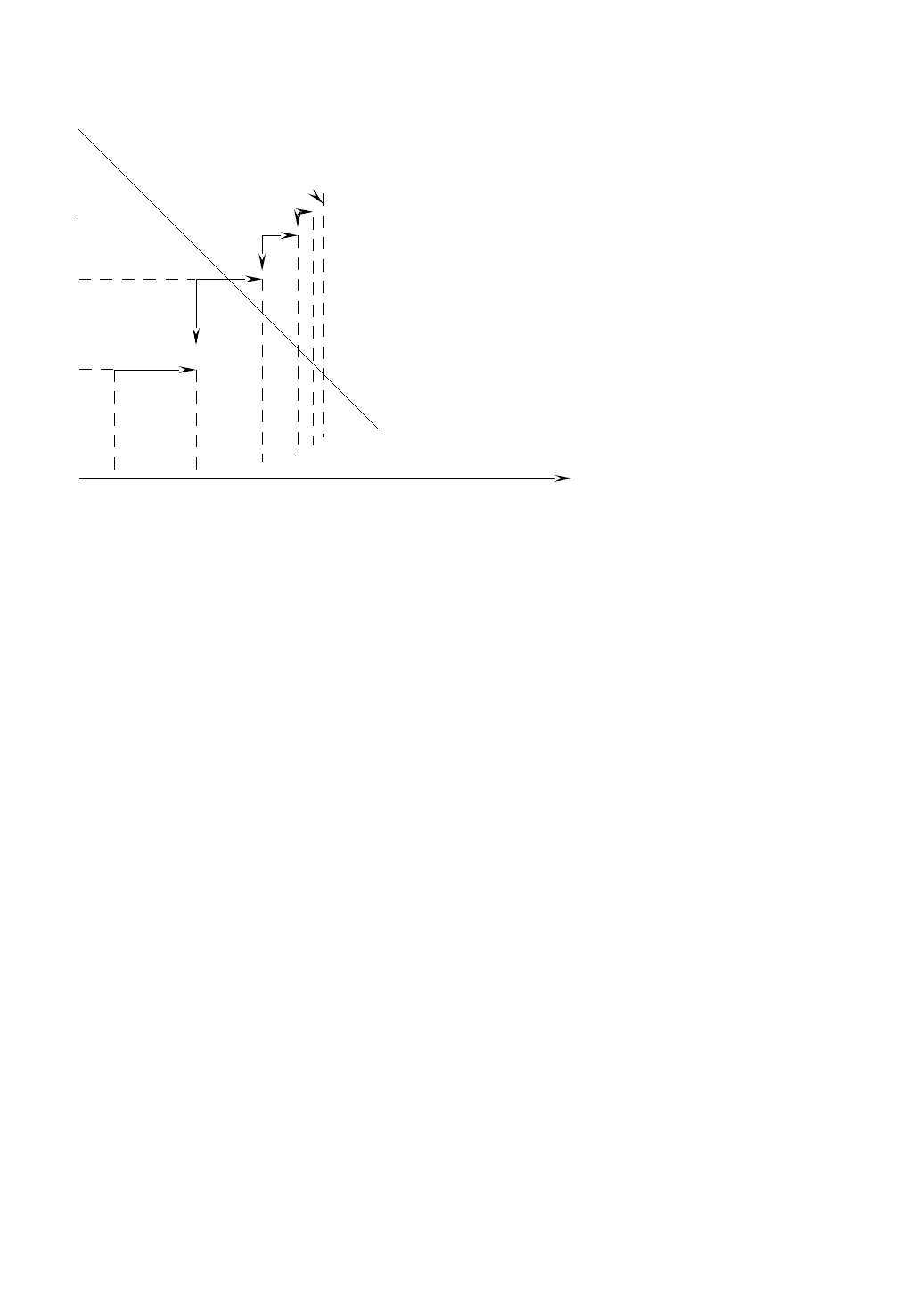
Рассмотрим геометрическое представление процесса решения. При решении
уравнения (1.2) отыскивается точка пересечения кривой
y=f ( x )
и прямой
y=x
.
Рассмотрим рис. 1.1, на котором изображена некоторая кривая
y=f ( x )
. Кривая
эта может представлять собой какую угодно функцию. Пусть
x=a
значение
x
в
точке пересечения, тогда
a
является корнем этого уравнения.
Естественно, что при решении задачи корень неизвестен.
Зададимся некоторым
x
0
Значение
x
1
равно
f (x
0
)
. Так как
0 A
(рис. 1.1)
равно
f (x
0
)
, то найти
x
1
можно следующим образом: проведем через точку
A
горизонтальную линию до пересечения с прямой
y=x
в точке
B
, как показано
на рисунке. Значение
x
2
=f ( x
1
)
можно найти, проведя через точку
B
вертикальную линию до пересечения с кривой
y=f ( x )
. При этом получим отрезок
0C
, равный
f (x
1
)
, и проводя через точку
C
горизонтальную линию до
пересечения с прямой
y=x
, получим
x
2
. Процесс продолжается в этом же
порядке и дальше; на рисунке последовательность операцией изображена стрелка-
ми.
Для сходимости процесса решения необходимо и достаточно, чтобы
|f
'
( x)|<1
.
Таким образом, перед началом решения требуется найти такое значение
аргумента, при котором значение
|f
'
( x)|<1
.
4
Рис.1.1. Геометрическое представление метода
последовательных приближений.
Пример.
Пусть требуется найти ближайший корень трансцендентного уравнения
2e
−x
+cos x=0
Произведем замену
2e
−x
+cos x+x =x
x=f ( x),
где
f (x )=2 e
−x
+cos x+ x.
Найдем значение
f
'
( x )
f
'
( x)=−2 e
−x
−sin x+1 .
Составим блок-схему и программу нахождения ближайшего корня трансцен-
дентного уравнения (рис. 1.2).
y = f(x)
B
x
0
x
1
x
2
x
3
x
4
x
C
A
y
y = x
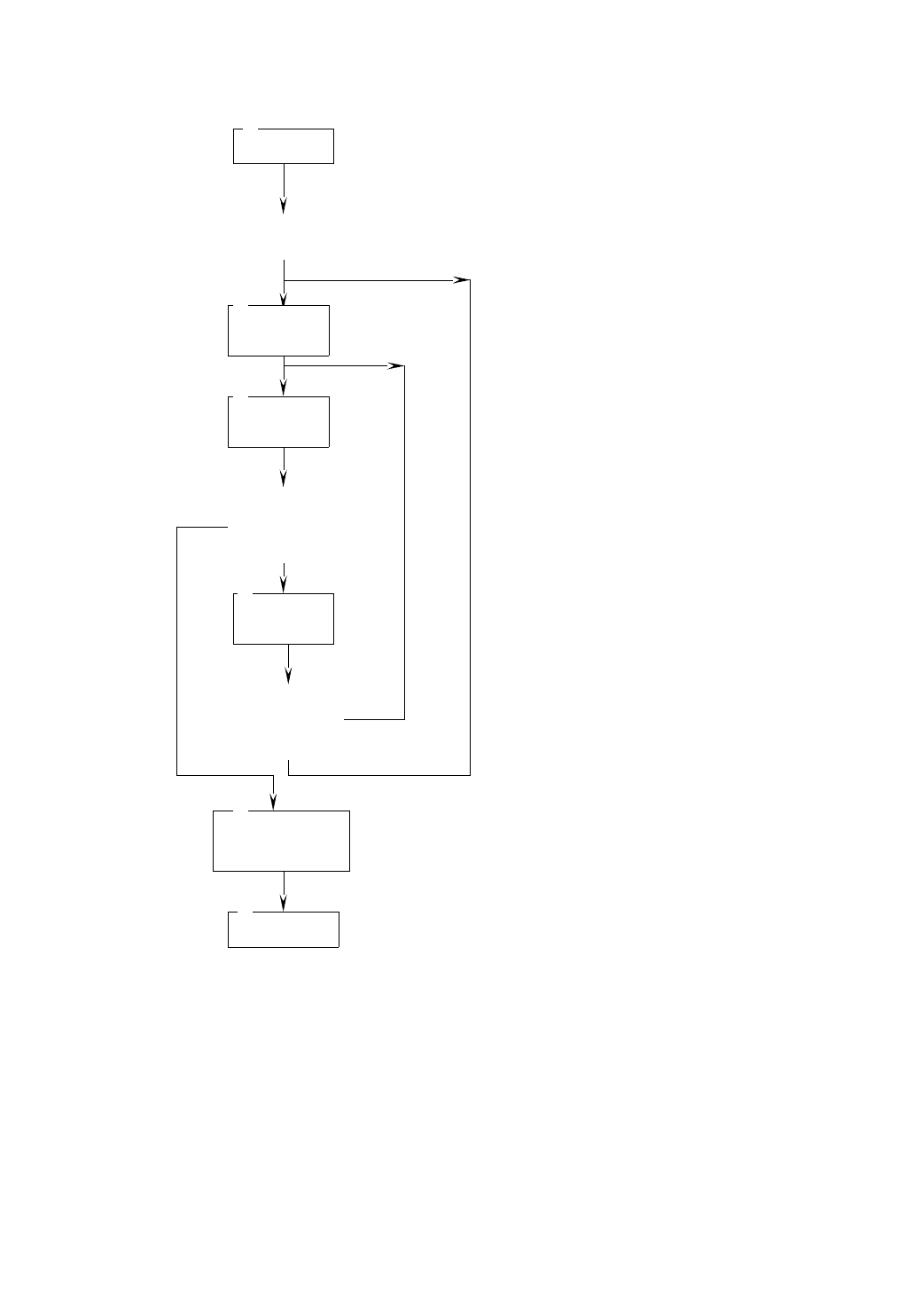
5
Рис. 1.2 блок-схема решения уравнений методом
последовательных приближений.
В блоке 2 (рис.1.2) производится ввод начального приближения x
0
и требуемой
точности нахождения решения уравнения (1.2), а в блоках 3 и 4 – вычисление
значений функции f(x) и ее производной f
(x). После вычисления значений функции
и ее производной в блоке 5 производится анализ равенства аргумента и функции.
Если равенство достигнуто, осуществляется переход к блоку 8 и значения аргумента
и функции выводятся на печать. Если же нет, то значению аргумента присваивается
значение функций (блок 6) и осуществляется проверка сходимости (блок 7). Если
нет
да
да
f(x)<1
/f(x)-x/
<z
x, z
пуск
1
f(x) =
f(x) =
x =f(x)
x, f(x)
останов
9
8
7
6
5
4
3
2

6
сходимость при данном начальном приближении обеспечивается, то осуществляется
переход к блоку 4 и начинается поиск решения уравнения. Если же нет, то
происходит возврат к блоку 3, где вычисляется значение производной при новом
приближении аргумента. Процесс поиска продолжается до тех пор,пока не будет
найдено начальное приближение,обеспечивающее сходимость процесса решения,
т.е. когда f
(x) <1.
К достоинствам метода последовательных приближений относятся его простота
и малый объем начальной информации.
Основным недостатком является необходимость анализа сходимости решения.
Для составления программы решения уравнения (1.5) введем некоторые
переобозначения f(x)
F, f
(x) = F1, x x и z - точность решения.
05 PRINT “РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ПП”
10 PRINT “ВВЕДИТЕ X, Z”
15 INPUT X, Z
20 LET F1 = –2*EXP(–X) – SIN (X) + 1
25 LET F = 2*EXP (–X) +COS (X) + X
30 IF ABS (F – X) < Z THEN 50
35 LET X = F
40 IF F1 >= 1 THEN 20
45 GOTO 25
50 PRINT “X” = X, “F” = F
55 END
Задание к лабораторно-практическому занятию:
1. Изучить метод последовательных приближений.
2. Выбрал уравнение:
f (x )= sin 0.1 x +e
−0. 4 x
+0. 2;
3. Составить блок-схему и программу решения уравнения на ЭВМ.
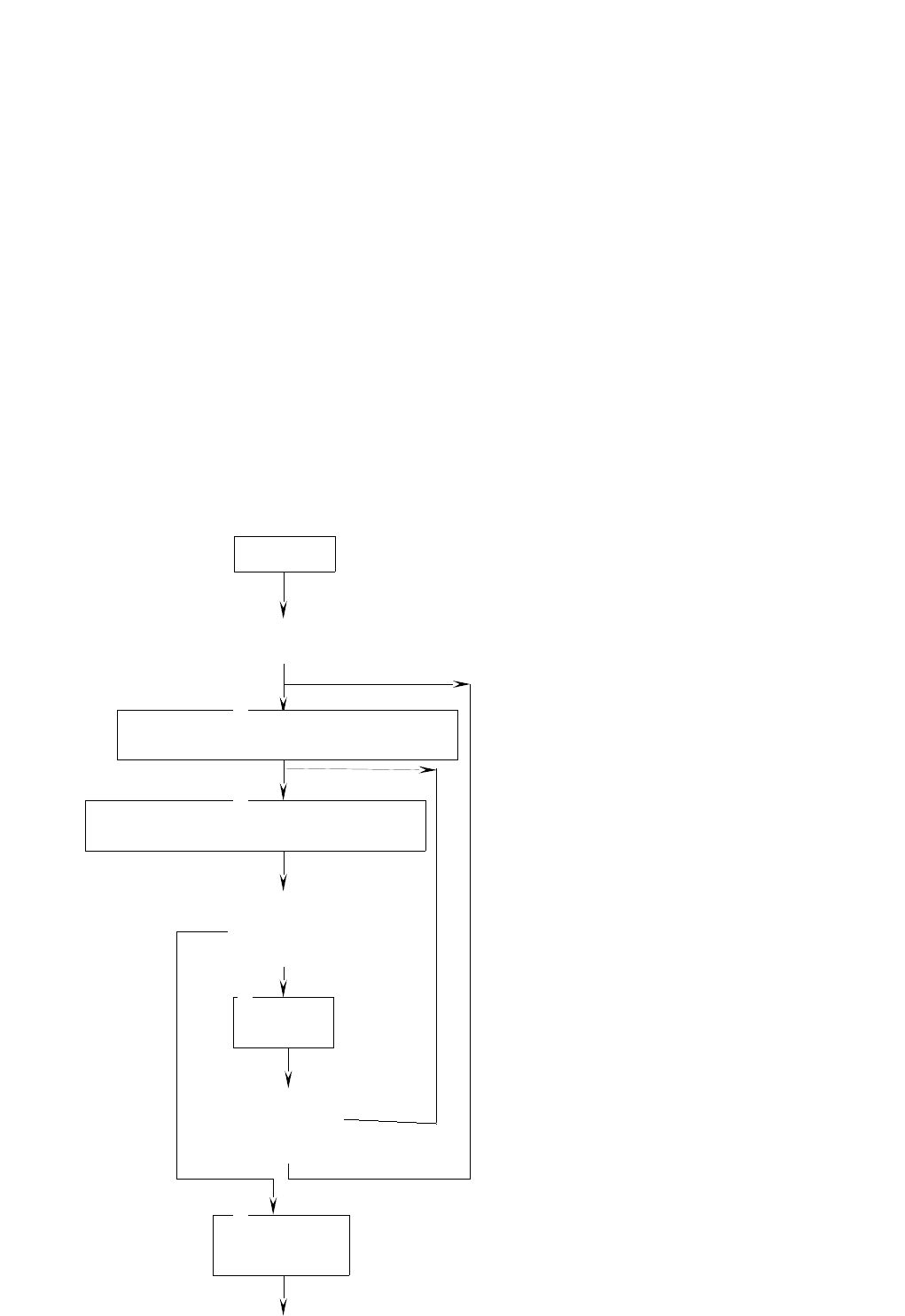
7
4. Ввести программу в ЭВМ и получите решение.
Пункты 1-3 выполняются в процессе самостоятельной подготовки к
лабораторно-практическойу занятию.
2 ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
1. Изучил метод последовательных приближений.
2. Выбрал уравнение:
f (x )=sin 0.1 x+e
−0. 4 x
+x +0.2 ;
И на его основе вычел производную:
f
'
( x)=cos0.1 x +e
−0. 4 x
+1;
3. Составил блок-схему и программу решения уравнения на ЭВМ:
нет
да
да
f(x)<1
f(x)-x<z
x, z
1
f(x) =cos(0.1*x)+exp(-0.4*x)+1
f(x) =sin(0.1*x)+exp(-0.4*x)+x+0.2
x =f(x)
x, f(x)
8
7
6
5
4
3
2
пуск

8
4. Ввести программу в ЭВМ:
PRINT "Reshenie yravneniya metodom PP"
PRINT "Vvedite X,Z"
INPUT X, Z
20 f1 = COS(.1 * X) + EXP(-.4 * X) + 1
25 f = SIN(.1 * X) + EXP(-.4 * X) + .2 + X
IF ABS(f - X) < Z THEN 50
X = f
IF f1 >= 1 THEN 20
GOTO 25
50 PRINT "x="; X, "f="; f
END
И получил решение x=33.4305 и f(x)=33.4304
ВЫВОДЫ
В результате этой лабораторной работы была написана программа которая
решала уравнение методом последовательных приближений, который при
определенных условиях выдает достаточно точный ответ.
останов
9
