Лабораторная работа - Фракталы
Подождите немного. Документ загружается.

1 Цель занятия
Реализовать фракталы.
Краткая теория
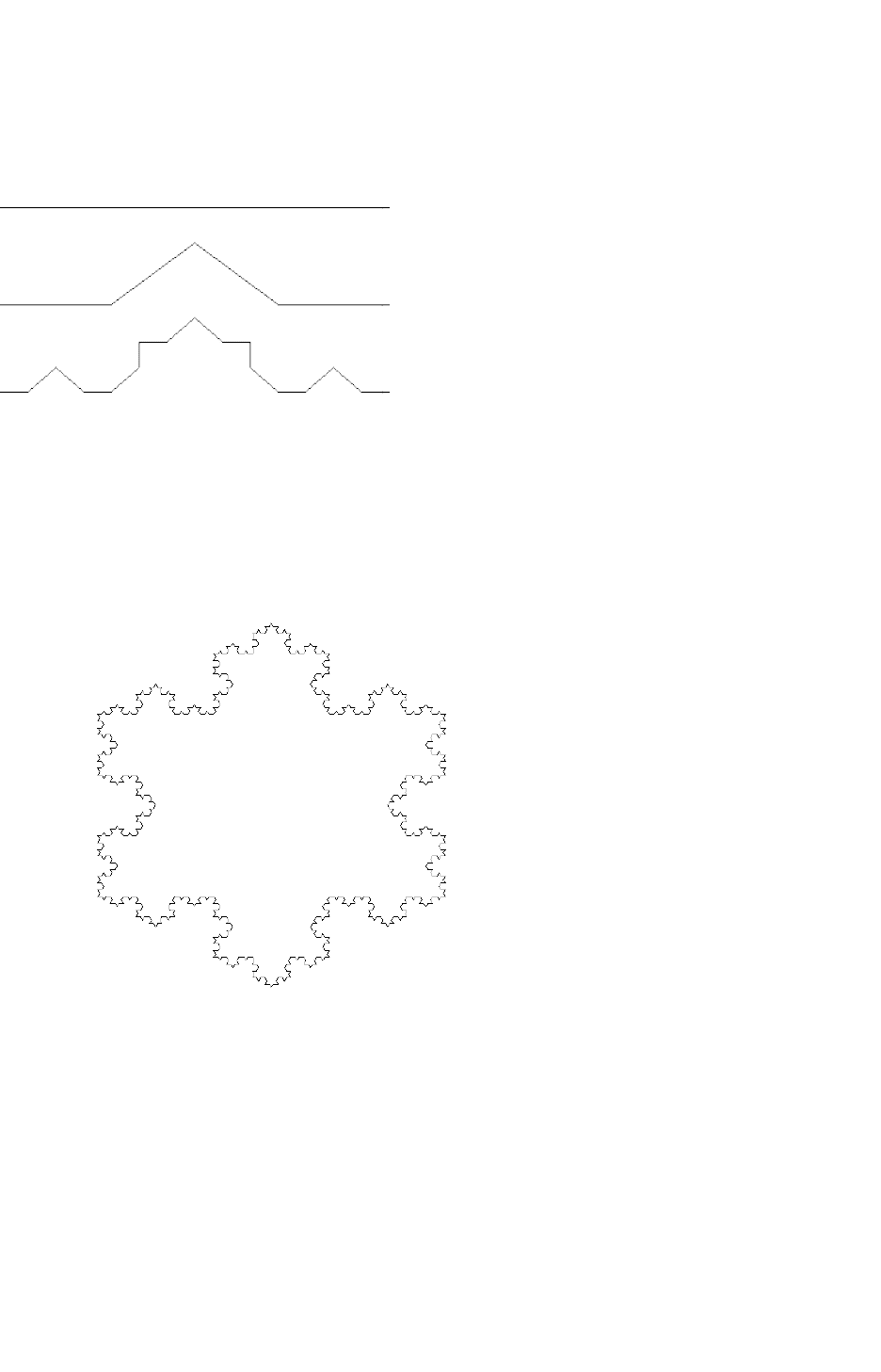
Рассмотрим классический пример фрактального множества - триадную кривую Кох (рис. 1).
Рис. 1. Построение триадной кривой Кох
Построение кривой начинается с единичного
отрезка, который называется инициатором и является
предфракталом 0-го порядка. Далее инициатор
заменяется на образующий элемент - кривую из четырех
прямолинейных звеньев, каждое из которых имеет длину
1/3. Так образуется предфрактал 1-го порядка. Его длина равна 4/3. Для построения предфрактала
следующего порядка каждое звено заменяется на уменьшенный образующий элемент. В результате
получаем кривую, состоящую из 4 x 4 = 16 звеньев, каждое из которых имеет длину (1/3) / 3 = 1/9, общая
длина равна 16/9. Длина предфрактала n-го порядка равна (4/3) в степени n. Очевидно, что предел длины
кривой при n, стремящемся к бесконечности, равен бесконечности. В итоге получили кривую бесконечной
длины, заполняющую ограниченное множество на плоскости, что само по себе очень любопытно. Если
построение кривой начинать не с отрезка, а с треугольника, и применить вышеперечисленные построения к
каждой его стороне, то получим "снежинку" Кох (рис. 2).
Рис. 2. "Снежинка" Кох
(Предфрактал 4-го порядка)
Эта фигура интересна
тем, что ее периметр - линия
бесконечной длины -
ограничивает конечную
площадь. В [3] показано, что
фрактальная размерность
триадной кривой Кох D равна
ln4/ln3, то есть D является
дробным числом,
находящимся между 1 и 2.

Ковер Серпинского:
Листинг программы:
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls;
type
TForm1 = class(TForm)
Image1: TImage;
// Image1: TImage;
procedure ris(x1,y1,x2,y2,n:integer);
procedure FormShow(Sender: TObject);

//procedure FormShow(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure Tform1.ris(x1,y1,x2,y2,n:integer);
var
x11,x22,y11,y22:integer;
begin
x11:=round(x1*2/3+x2/3);
x22:=round(x1/3+x2*2/3);
y11:=round(y1*2/3+y2/3);
y22:=round(y1/3+y2*2/3);
Image1.Canvas.Rectangle(x11,y11,x22,y22);
if n<>0 then
begin
ris(x1, y1, x11, y11, n-1);
ris(x11, y1, x22, y11, n-1);
ris(x22, y1, x2, y11, n-1);

ris(x1, y11, x11, y22, n-1);
ris(x22, y11, x2, y22, n-1);
ris(x1, y22, x11, y2, n-1);
ris(x11, y22, x22, y2, n-1);
ris(x22, y22, x2, y2, n-1);
end;
end;
procedure TForm1.FormShow(Sender: TObject);
begin
Image1.Canvas.Rectangle(0,0,300,300);
ris(0,0,300,300,4);
end;
end.
Снежинка Коха

Листинг программы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls;
type
toch=record
x,y:integer;
end;
poch=^och;
och=record

n,k:toch;
next:poch;
end;
TForm1 = class(TForm)
Image1: TImage;
procedure FormShow(Sender: TObject);
procedure int();
procedure pop();
procedure push(f,e:toch);
procedure ris();
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
pbegin,pend,p:poch;
a,b,v,m:toch;
implementation
{$R *.dfm}
procedure TForm1.FormShow(Sender: TObject);
var
i:integer;

begin
int();
Image1.Canvas.MoveTo(100,200);
for i:=1 to StrToInt(Form1.Caption) do
begin
pop();
ris();
end;
end;
procedure TForm1.int();
begin
new(p);
p.n.x:=100;
p.n.y:=200;
p.k.x:=700;
p.k.y:=200;
p.next:=pend;
pend:=p;
pbegin:=p;
new(p);
p.n.x:=700;
p.n.y:=200;
p.k.x:=400;
p.k.y:=719;
pend.next:=p;
pend:=p;
new(p);

p.n.x:=400;
p.n.y:=719;
p.k.x:=100;
p.k.y:=200;
pend.next:=p;
pend:=p;
end;
procedure Tform1.pop();
begin
a.x:=pbegin.n.x;
a.y:=pbegin.n.y;
b.x:=pbegin.k.x;
b.y:=pbegin.k.y;
pbegin:=pbegin.next;
end;
procedure Tform1.push(f,e:toch);
begin
new(p);
p.n:=f;
p.k:=e;
pend.next:=p;
pend:=p;
end;
procedure Tform1.ris();
begin

v.x:=b.x-a.x;
v.y:=b.y-a.y;
Image1.Canvas.MoveTo(a.x,a.y);
Image1.Canvas.Pen.Color:=clWhite;
Image1.Canvas.LineTo(b.x,b.y);
Image1.Canvas.MoveTo(a.x,a.y);
Image1.Canvas.Pen.Color:=clBlack;
b.x:=a.x+round(v.x*1/3);
b.y:=a.y+round(v.y*1/3);
Image1.Canvas.LineTo(b.x,b.y);
push(a,b);
a:=b;
b.x:=b.x+round(((v.x/2)-(v.y*sqrt(3)/2)*(-1))/3);
b.y:=b.y+round((v.y/2-(v.x*(sqrt(3)/2)))/3);
Image1.Canvas.LineTo(b.x,b.y);
push(a,b);
a:=b;
b.x:=b.x+round(((v.x/2)+(v.y*sqrt(3)/2)*(-1))/3);
b.y:=b.y+round((v.y/2+v.x*sqrt(3)/2)/3);
Image1.Canvas.LineTo(b.x,b.y);
//ShowMessage(IntToStr(m.x)+' '+IntToStr(m.y));
push(a,b);
a:=b;
b.x:=b.x+round(v.x*1/3);

b.y:=b.y+round(v.y*1/3);
Image1.Canvas.LineTo(b.x,b.y);
//ShowMessage(IntToStr(m.x)+' '+IntToStr(m.y));
push(a,b);
end;
end.
Папоротник
