Лабораторная работа - Ценообразование.Метод статистических игр и его использование при обосновании скидок с цен
Подождите немного. Документ загружается.

Кафедра менеджмента
УПРАВЛЕНИЕ ЦЕНООБРАЗОВАНИЕМ
Лабораторная работа
Метод статистических игр и его использование при
обосновании скидок с цен
г. Владимир, 2010
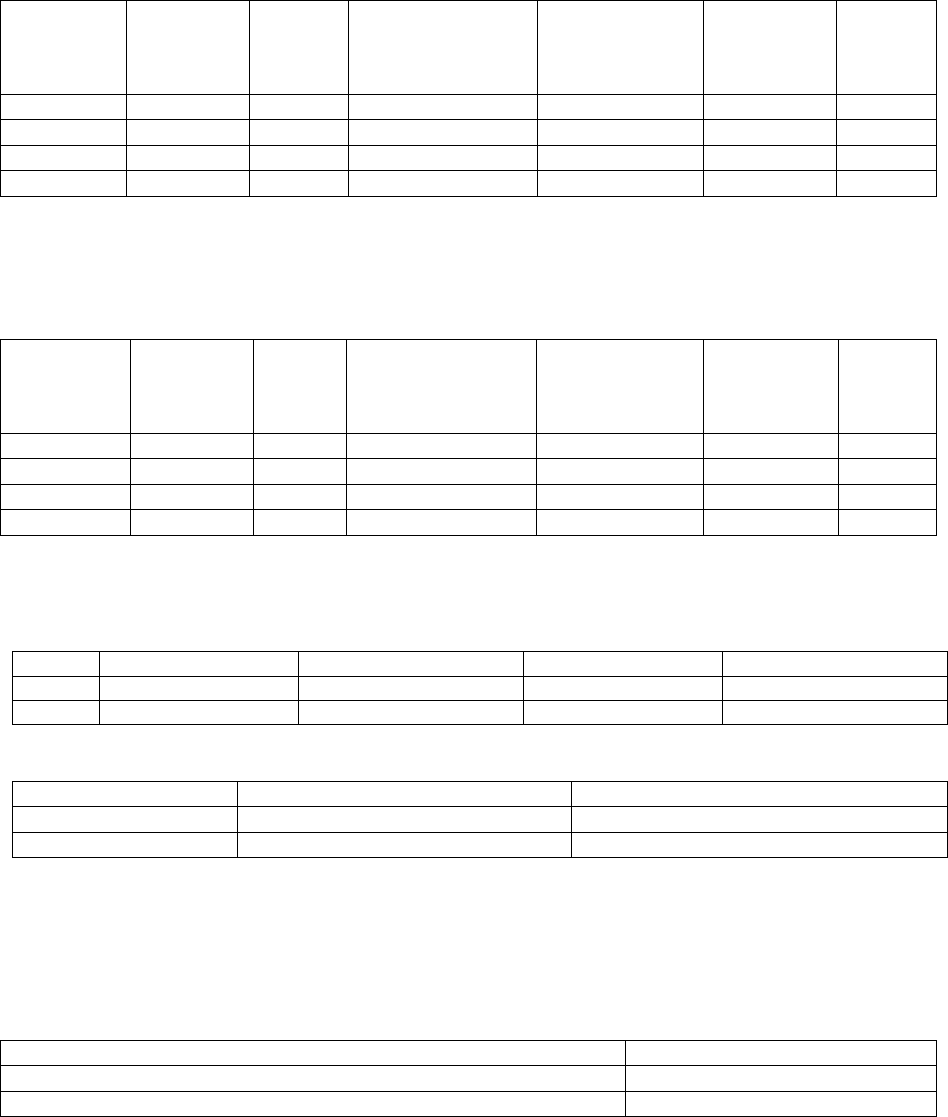
Определить предполагаемый объем продажи платьев (штук) в результате снижения цен, если
известно, что:
количество нераспроданных платьев — 870 штук;
закупочная цена товара — 122 руб.;
продажная цена товара — 240 руб.;
решение торгового предприятия о снижении продажной цены на: 5, 15, 20, 25%;
коэффициенты эластичности (по данным конъюнктурного института) при малой
эластичности спроса от цены на аналогичные товары в размере 1; 1; 1,1; 1 и при высокой
эластичности спроса от цены в размере 1,7; 2,1; 2; 1,5;
Таблица 1.Состояние природы θ
1
Решение
статистика
Снижение
цены Р, %
Новая
цена,
руб.
Предполагаемый
объем продаж в
результате
снижения Р, шт.
Предлагаемый
объем продаж,
руб. (гр.3хгр.4)
Закупочная
цена товара,
руб.
(870х122)
Потери,
руб.
(гр.6-
гр.5)
а
1
5 228 43,5 9918 106140 96222
а
2
15 204 130,5 26622 106140 79518
а
3
20 192 194,4 37324,8 106140 68815,2
а
4
25 180 217,5 39150 106140 66990
Новая цена (руб.) = средняя продажная цена*(100-а
j
) /100
Предполагаемый объем продаж в результате снижения цен =
Таблица 2.Состояние природы θ
2
Решение
статистика
Снижение
цены Р, %
Новая
цена,
руб.
Предполагаемый
объем продаж в
результате
снижения Р, шт.
Предлагаемый
объем продаж,
руб. (гр.3хгр.4)
Закупочная
цена товара,
руб.
(870х122)
Потери,
руб.
(гр.6-
гр.5)
а
1
5 228 73,95 16860,6 106140 89279,7
а
2
15 204 274,05 55906,2 106140 50233,79
а
3
20 192 348 66816 106140 39324
а
4
25 180 326,25 58725 106140 47415
Значения функции потерь L(θ, a
i
) запишем в матрицу (тыс. руб.) (табл. 3).
Таблица 3. Значения функции потерь L(θ, a
i
)
a1 a2 a3 a4
θ1 96222 79518 68815,2 66990
θ2 89279,7 50233,79 39324 47215
Таблица 4. Редуцированная матрица значений функций потерь
a3 a4
θ1 68815,2 66990
θ2 39324 47215
Учитывая возможность ошибок при проведении единовременного анкетного опроса случайно
отобранных покупателей, примем следующие условные распределения результатов х
1
и х
2
в
зависимости от действительного состояния природы θ
1
и θ
2
т. е. от низко- или высокоэластичного
спроса. Приведенные условные распределения результатов x
1
и х
2
в зависимости от
действительного состояния природы θ
1
и θ
2
являются априорными величинами, полученными на основе
многих ранее проведенных, к примеру конъюнктурным институтом, наблюдений.
P{x1|Q1} 0,7
P{x1|Q2} 0,3
P{x2|Q1} 0,2
ji
Эa

P{x2|Q2} 0,8
Таблица 5.Нерандомизированные функции
d1 d2 d3 d4
x1 а
3
а
3
а
4
а
4
x2 а
3
а
4
а
3
а
4
d1 d2 d3 d4
x1 68815,2 68815,2 66990 66990
x2 68815,2 66990 68815,2 66990
d1 d2 d3 d4
x1 39324 39324 47215 47215
x2 39324 47215 39324 47215
Для каждой из этих четырех нерандомизированных функций решения можно с учетом обоих
состояний природы θ
1
, и θ
2
вычислить значения функции риска
R(θ,d). Вычислим значения функции риска:
R(θ
1
, d
1
) = 68815,2*0,7 + 68815,2*0,3 = 68815,2
R(θ
1,
d
2
) = 68815,2*0,7 + 66990*0,3 = 68267,64
R(θ
1
,d
3
) = 66990*0,7 + 68815,2*0,3 = 67537,56
R(θ
1,
d
4
) = 66990*0,7 + 66990*0,3 = 66990
R(θ
2
,d
1
) = 39324*0,2 + 39324*0,8 = 39324
R(θ
2
,d
2
) = 39324*0,2 + 47215*0,8 = 45636,8
R(θ
2
, d
3
) = 47215*0,2 + 39324*0,8 = 40902,2
R(θ
2
,d
4
) = 47215*0,2 + 47215*0,8 = 47215
Значения функции риска R(θ,d) запишем в матрицу:
Таблица 6. Значения функции риска R(θ,d)
d1 d2 d3 d4
Q1
68815,2 68267,64 67537,56 66990
Q2
39324 45636,8 40902,2 47215
Оптимальным будет решение о размере сезонного снижения цен на летние платья, которое в
максимальной мере оберегает торговое предприятие от высоких потерь. Наиболее осторожной
функцией решения будет минимаксная стратегия статистика. Выбираем для каждого столбца
матрицы значений функции риска «наибольший» элемент, а затем среди них выбираем
минимальный элемент, тем самым определяем столбец d
i
с этим минимальным элементом.
В решаемой задаче среди максимальных элементов минимальным является число 66990. Этому
числу соответствует нерандомизированная минимаксная функция решения d
4
.
Так как эта функция определялась следующим образом:
d
4
(x
1
) = а
3
и d
4
(x
2
) = а
3
,
то это означает, что оптимальной в данном случае, т. е. наиболее осторожной, стратегией
торгового предприятия, намечающего сезонное снижение цен на летние женские платья, будет
снижение цен на 25% безотносительно к результатам анкеты: как в случае, когда анкета оценила
спрос как малоэластичный, так и тогда, когда оценка указывала на высокоэластичный спрос.
