Курсовой проект - Расчет теплообменника

Подождите немного. Документ загружается.

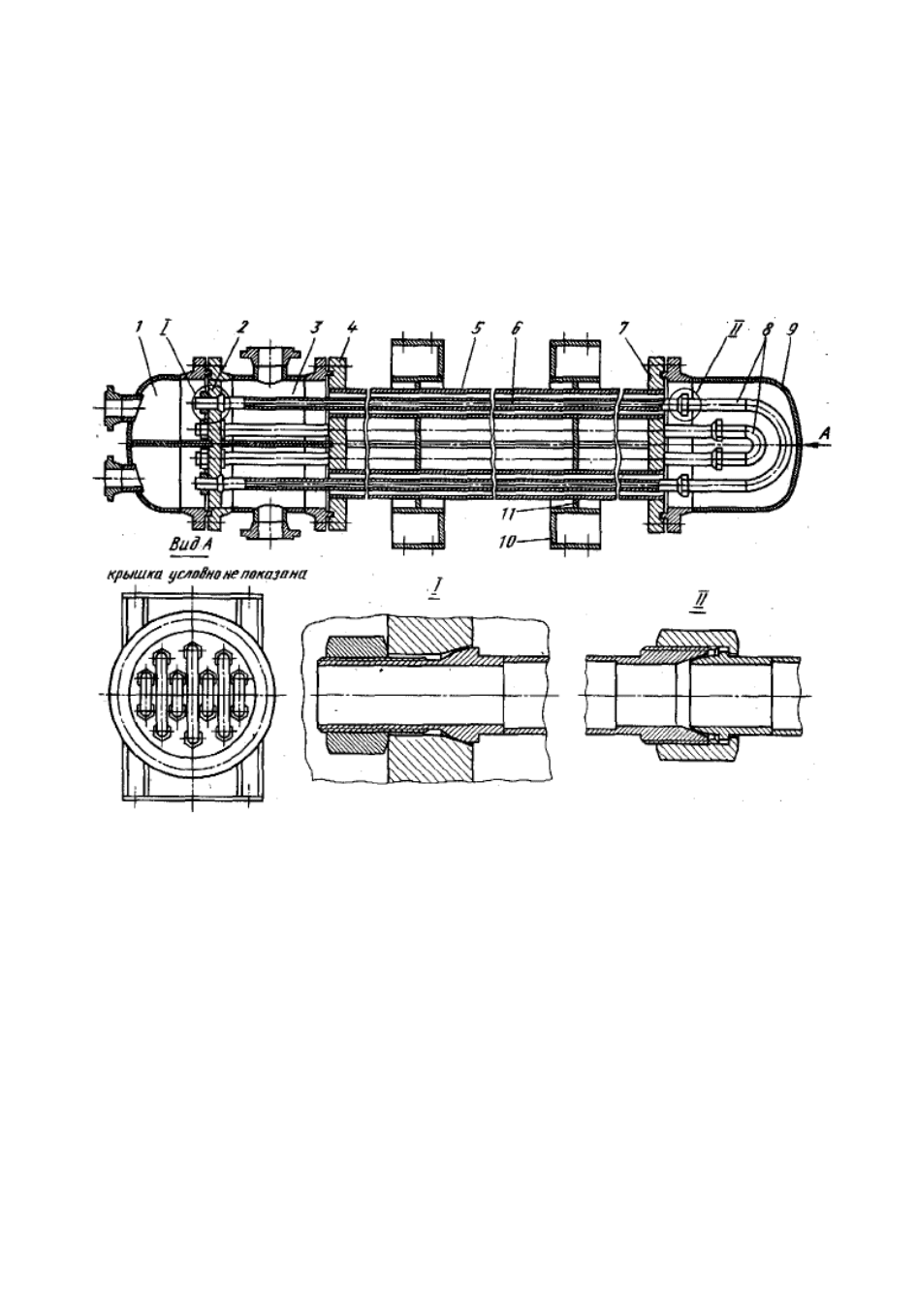
размещены теплообменные трубы 6, один конец которых

жестко связан с левой трубной решеткой 2, а другой — может

перемещаться. Свободные концы теплообменных труб

попарно соединены коленами 8 и закрыты камерой 9. Для

распределения потока теплоносителя по теплообменным

трубам служит распределительная камера 1, а для

распределения теплоносителя в межтрубном пространстве —

распределительная камера 3. Пластинами 11 кожуховые

трубы жестко связаны с опорами 10.

Рис. 3.8. Разборный двухпоточный теплообменник типа "труба в

трубе"

Теплообменник имеет два хода по внутренним трубам и

два по наружным. Узлы соединения теплообменных труб с

трубной решеткой (узел I) и с коленами (узел II) уплотнены за

счет прижима и деформации полушаровых ниппелей в

конических гнездах.

Эти аппараты могут работать с загрязненными

теплоносителями, так как внутреннюю поверхность

теплообменных труб можно подвергать механической

очистке. Поскольку возможность температурных удлинений

кожуховых труб из-за жесткого соединения их с опорами

ограниченна, перепад температур входа и выхода среды,

текущей по кольцевому зазору, не должен превышать 150 °С.

Довольно широкое применение в технике находят

ТЕПЛООБМЕННИКИ С НАРУЖНЫМИ ЗМЕЕВИКАМИ, применение

которых позволяет проводить процесс при высоких давлениях

(до 6 МПа). К стенкам аппаратов (обычно реакторов) снаружи

приваривают змеевики, изготовленные из полуцилиндров или

угловой стали. Если же необходимо использовать

теплоноситель при еще более высоком давлении (например,

перегретую воду при 25 МПа), то змеевик приваривают к

корпусу аппарата многослойным швом.

К достоинствам аппарата с приваренными змеевиками

следует отнести возможность распределения системы труб

змеевика на несколько секций, питаемых независимо друг от

друга. Включением и отключением отдельных секций

становится возможным регулировать обогрев или

охлаждение. Кроме того, материал привариваемых змеевиков

может быть отличным (более дешёвым) от материала корпуса

аппарата.

АППАРАТЫ С ДВОЙНЫМИ СТЕНКАМИ (РУБАШКАМИ)

используют в химической промышленности как обогреваемые

(охлаждаемые) сосуды для проведения химических реакций.

Как правило, они работают под избыточным давлением в

зависимости от характера технологического процесса носят

название автоклавов, полимеризаторов, и др.

Аппараты теплообменные листовые

СПИРАЛЬНЫЕ ТЕПЛООБМЕННИКИ изготовляют с

поверхностью теплообмена 10—100 м2; они работают как под

вакуумом, так и при давлении до 1 МПа при температуре

рабочей среды 20—200 °С. Их можно использовать для

реализации теплообмена между рабочими средами жидкость

—жидкость, газ—газ, газ—жидкость, а также конденсации

паров и парогазовых смесей. Все большее распространение

этих теплообменников в последнее время объясняется

главным образом простотой изготовления и компактностью

конструкции. В таком аппарате один из теплоносителей

поступает в периферийный канал аппарата и, двигаясь по

спирали, выходит из верхнего центрального канала. Другой

теплоноситель поступает в нижний центральный канал и

выходит из периферийного канала. Площадь поперечного

сечения каналов в таком теплообменнике по всей длине

постоянна, поэтому он может работать с загрязненными

жидкостями (загрязнение смывается потоком теплоносителя).

В спиральных теплообменниках поверхность теплообмена

образована двумя стальными лентами 1, 2 толщиной 3,5—6

мм и шириной 400—1250 мм (рис. 1.14), свернутыми в спираль

так, что получаются каналы а и б прямоугольного профиля, по

которым противоточно движутся теплоносители.

Первый (от центра аппарата) виток спирали закреплен

распорными дисками 4, которые фиксируются продольными

распорками 3. На поверхности спирали с шагом 70—100 мм

приварены штифты 6 для придания теплообменнику

жесткости. Кроме штифтов при навивке спирали между ее

витками устанавливают полосовые дистанционные вставки 5.

Эти вставки вместе со штифтами обеспечивают требуемый

зазор между лентами, который для стандартных

теплообменников составляет 8—12 мм. С торцов аппарат

закрыт крышками на прокладках. В зависимости от способа

уплотнения спиральных каналов с торцов различают

теплообменники с тупиковыми и сквозными каналами.

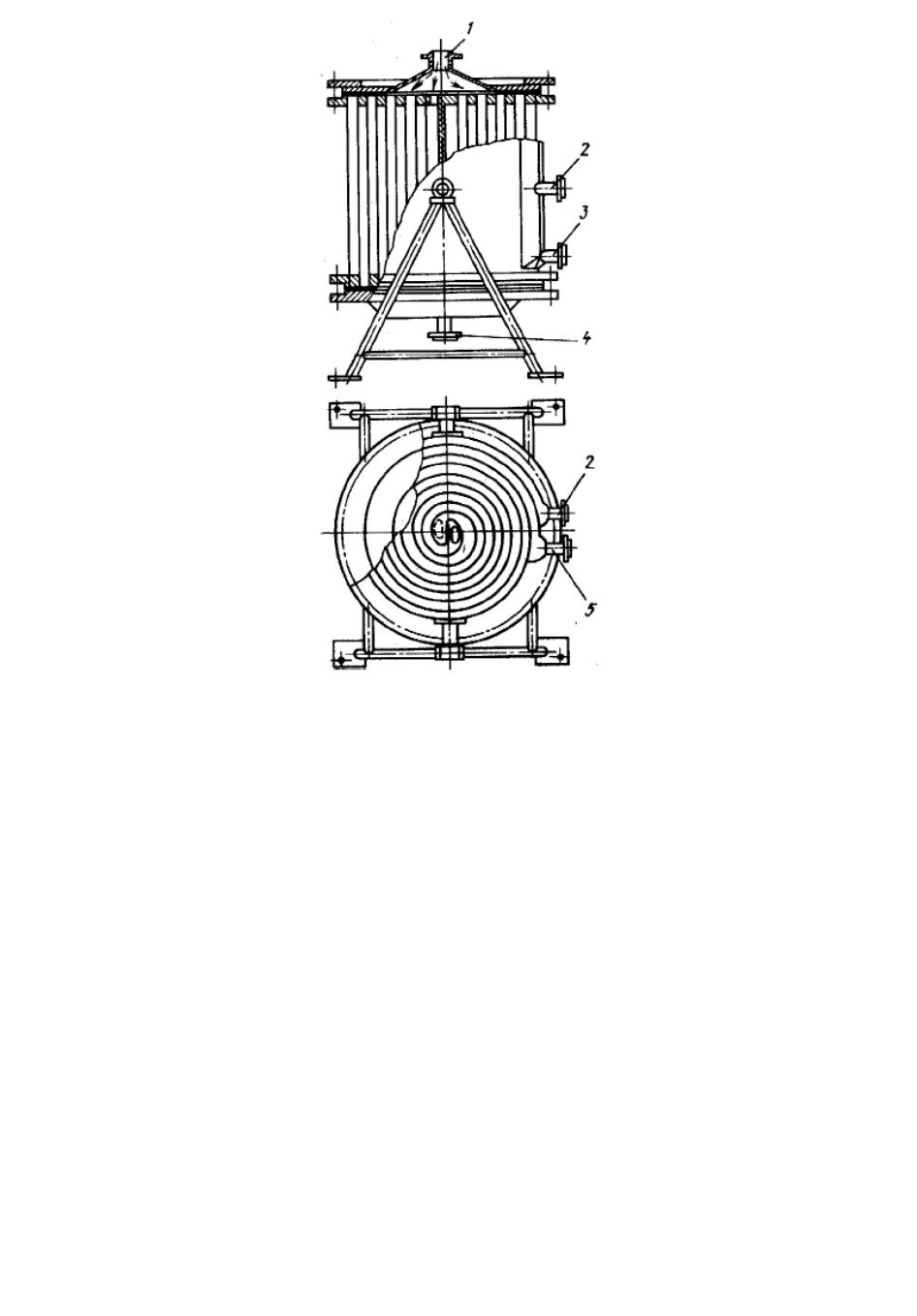
Рис.3.9 Спиральный теплообменник теплообменнике

Тупиковые каналы образуют приваркой полосовых вставок

к торцу спирали; с торцов каналы закрыты крышками с

прокладкой. После снятия крышек и прокладок оба канала

можно прочистить. Такой способ уплотнения каналов

исключает возможность смешения теплоносителей при

прорыве прокладки и поэтому наиболее распространен.

Сквозные каналы с обоих торцов закрыты крышками с

прокладками, легко поддаются чистке, но не исключают

возможность смешения теплоносителей.

Выбор теплообменного аппарата

Выбор оптимальной конструкции теплообменника

является задачей, разрешаемой технико-экономическим

сравнением нескольких типоразмеров аппаратов

применительно к заданным условиям или на основании

критерия оптимизации.

На поверхность теплообмена и на относящуюся к ней

долю капитальных затрат, а также на стоимость

эксплуатации влияет недорекуперация теплоты. Чем меньше

величина недорекуперации теплоты, т.е. чем меньше

разность температур греющего теплоносителя на входе и

нагреваемого теплоносителя на выходе при противотоке, тем

больше поверхность теплообмена, тем выше стойкость

аппарата, но тем меньше эксплуатационные расходы.

Конечно, должен быть определенный оптимум увеличения

капитальных и снижения эксплуатационных расходов,

который можно определить графически. Известно также, что

с увеличением числа и длины труб в пучке и уменьшением

диаметра труб снижается относительная стоимость 1 м2

поверхности кожухотрубчатого теплообменника, так как при

этом снижается общая затрата металла на аппарат в расчете

на единицу поверхности теплообмена. Следует иметь в виду,

что с увеличением числа труб увеличивается вероятность

нарушения плотности их крепления в трубной решетке, а с

применением труб малого диаметра увеличивается их

засоряемость и усложняется чистка.

При выборе типа теплообменника можно

руководствоваться следующим рекомендациями.

1. При обмене теплотой двух жидкостей или двух газов

целесообразно выбрать секционные (элементные)

теплообменники; если из-за большой поверхности

теплообменника конструкция получается громоздкой, можно

принять к установке многоходовой кожухотрубчатый

теплообменник.

2. При подогреве жидкости паром рекомендуются

многоходовые по трубному пространству кожухотрубчатые

аппараты с подачей пара в межтрубное пространство.

3. Для химически агрессивных сред и при небольших

тепловых производительностях экономически целесообразны

рубашечные, оросительные и погружные теплообменники.

4. Если условия теплообмена по обе стороны тепло-

передающей поверхности резко различны (газ и жидкость),

должны быть рекомендованы трубчатые ребристые

теплообменники.

5. Для передвижных и транспортных тепловых установок,

авиационных двигателей и криогенных систем, где при

высокой эффективности процесса

необходимы компактность и малая масса, находят широкое

применение

пластинчатые ребристые теплообменники.

6. Во всех случаях необходимо стремиться выбирать

наиболее простые по конструкции и наиболее дешевые по

материалам теплообменники. К усложненным аппаратам (с

плавающей камерой, с сильфонным компенсатором,

спиральным), а также с латунными или медными трубами

следует прибегать лишь в случае обоснованной

необходимости.

Исходя из всего перечисленного для данных условий был

выбран кожухотрубчатый конденсатор с неподвижными

трубными решетками.

4. Технологический расчет.

Расчет теплообменного аппарата выполняется в

определенной последовательности. Упорощенная схема

расчета состоит из следующих этапов.

1. Нахождение теплотехнических свойств (p,c,r,μ,λ)

индивидуальных веществ и их смесей.

2. Определение тепловой нагрузки Q, неизвестного

расхода теплоносителя или хладоагента, принятие

коэффициента теплопередачи, расчет ориентировочной

поверхности теплопередачи, выбор типа

теплообменника.

3. Определение режимов движения горячего и холодного

потоков, расчет коэффициентов теплоотдачи, а затем

теплопередачи, определение температуры стенки и

уточнение найденных ранее коэффициентов.

4. Определение уточненной площади поверхности

теплопередачи и расчет запаса.

5. Выбор диаметров штуцеров и расчет гидравлического

сопротивления трубного и межтрубного пространств.

6. Технико-экономический расчет и выбор оптимальной

конструкции аппарата.

7. Заполнение «Бланка заказа для изготовления

стандартного кожухотрубчатого теплообменника».

Выражение состава пара в мольных долях yi

Молярные массы компонентов: бензола M1=78,11

кг/кмоль, толуола М2=92,13 кг/кмоль. Мольные доли

компонентов yk находятся пересчетом из массовых процентов

ỹk, указанных в задании, по формуле:

yk=( ỹk/Mi)/∑ ỹk/Mi,

(1)

где Mi – мольная масса компонента i (кг/кмоль).

y1=(98,5/78,11)/(98,5/78,11+1,5/92,13)=0,99;

y2=(1,5/93,13)/(1,5/92,13+98,5/78,11)=0,01.

Проверка: y1+y2=1,0.

0,99+0,01=1.

Определение температуры начала конденсации пара

Принимаем температуру начала конденсации пара t`н=80˚С. По

уравнению Антуана рассчитываем при этой температуре давление

насыщенных паров компонентов:

lnP=A-B/(T+C), (2)

где Р – давление насыщенного пара, мм рт. Ст.;

А, В, С – константы, зависящие от природы вещества;

Т – температура, К.

mi=Pi/П, (3)

где mi – константы фазового равновесия компонентов смеси для

произвольной температуры t;

Рi – давление насыщенного пара i-того компонента при температуре t;

П – общее давление в системе.

∑yi/mi=1,0, (4)

где yi – мольная доля i-того компонента пара, поступающего в аппарат;

mi – константа фазового равновесия i-того компонента.

lnP1= 15,9008 - 2788,5.1/[(80 + 273) - 52,36]

6,63,

откуда Р1 = е

6,63

= 934,5 мм рт. ст. =934,5 · 133,3=100974,75 Па;

lnP2= 16,0137 -, 3096,52/[(80 + 273) - 53,67] = 5,67;

откуда Ра = е

5,67

= 368,7мм.рт. ст. = 368,7 · 133,3 = 38661,6 Па.

По уравнению (3) рассчитываем константы фазового равновесия

компонентов при температуре t`н=85˚С:

m1 = 100974,75/115000 =0,878;

m2= 38661,6/115000=0,336.

По уравнению (4) рассчитываем:

0,99/0,878+0,01/0,336=1,16.

Найденная сумма значительно отличается от единицы, поэтому

принимаем новое значение температуры начала конденсации пара, равное

t``н=95˚С. Для температуры t``н=95˚С снова рассчитываем давление

насыщенных паров и константы фазового равновесия компонентов.

lnP1= 15,9008 - 2788,5.1/[(95 + 273) - 52,36]

7,07,

откуда Р1 = е

7,07

= 1176,15 мм рт. ст. =1176,15 · 133,3=156780,8 Па;

lnP2= 16,0137 -, 3096,52/[(95 + 273) - 53,67] = 6,16;

откуда Ра = е

6,16

= 473,43 мм.рт. ст. = 473,43· 133,3 = 63107,96 Па.

По уравнению (3) рассчитываем константы фазового равновесия

компонентов при температуре t`н=95˚С:

m1 = 156780,8/115000 =1,36;

m2= 63107,96/115000=0,55.

По уравнению (4) рассчитываем:

0,99/1,36+0,01/0,55=0,748.

Методом линейной интерполяции определяем температуру tн, при

которой сумма y1/m1+y2/m2 равна единице.

tн=95+[(0,748-1,0)·(80-95)/(0,748-1,16)]=85,8˚С;

tн=80-[(1,0-1,16)·(80-95)/(0,748-1,16)]=85,8˚С.

Температура tн=85,8˚С является температурой начала конденсации пара.

Определение температуры конца конденсации пара

Температура конца конденсации пара tw определяется методом

последовательных приближений с помощью уравнения:

∑х i*mi=1,0,

(5)

где хi – мольная доля i-того компонентав образовавшемся конденсате;

при полной конденсации паровой смеси получаемый конденсат имеет такой

же состав, что и паровая смесь, из которой был получен конденсат, т.е. хi=yi;

mi – константа фазового равновесия i-того компонента.

Принимаем температуру t`w=95˚С. Для этой температуры уже

были рассчитаны константы фазового равновесия компонентов. Рассчитываем

сумму

∑хi*mi=0,99·0,73+0,01·0,18=0,7245.

Найденная сумма значительно отличается от единицы, поэтому

принимаем новое значение температуры конца конденсации пара, равное

t``w=80˚С.

∑хi*mi=0,99·0,878+0,01·0,336=0,87236.

Методом линейной интерполяции определяем температуру tw, при

которой сумма x1·m1+x2·m2 равна единице.

tн=95+[(0,7245-1,0)·(80-95)/(0,7245-0,87236)]=80,06˚С;

tн=80-[(0,87236-0,7245)·(80-95)/( 0,7245-0,87236)]=80,06˚С.

Температура tw=80,06˚С является температурой конца конденсации пара.

Изменение температуры пара незначительно (от tн=85˚С до tw=80,06˚С), поэтому

среднюю температуру конденсации пара можно найти как среднюю

арифметическую:

tп=(tн+tw)/2; (6)

tп=(85+80,06)/2=82,93˚С.

В последующем расчете среднюю температуру конденсации пара tп

следует уточнить.

Расчет теплового потока и расхода хладоагента. Расчет температуры

воды в момент конденсации пара

Для определения теплового потока Q, передаваемого от

конденсирующегося пара к охлаждающей воде, рассчитываем по уравнению

удельную теплоту конденсации пара.

rсм=∑ri·yi,

(7)

i=1

где ri – удельная теплота конденсации i-того компонента пара, кДж/кг

или Дж/кг.

yi – массовая доля i-того компонента в паре;

p – число компонентов в паре.

Удельная теплота конденсации компонентов пара при температуре

tп=82,93˚С:

r1=393 кДж/кг; r2=378 кДж/кг;

rсм=393·0,985+0,015·378=392,75 (кДж/кг).

Тогда тепловая нагрузка аппарата Q