Курсовой проект - Проектирование преобразователя частоты на основании инвертора тока. Вариант 22
Подождите немного. Документ загружается.


прагне до 90 ел. градусів. Як відомо, при цьому суттєво зростає амплітуда
пульсацій і виникає небезпека виходу випрямляча в режим переривчастого
струму, що може приводити до порушення нормальної роботи інвертора.
Таким чином, недоліками амплітудного способу регулювання є, по-перше,
необхідність збільшення індуктивності Ld при глибокому регулюванні напруги
джерела харчування та, по-друге, пов'язана з цим мала швидкодія системи
стабілізації, що приводить до викидів і провалів у вихідній напрузі при різкій
зміні струму навантаження. Зазначені ефекти можуть бути зменшені при
використанні широтно-імпульсного регулятора за рахунок підвищення несучої
частоти, однак при цьому зростає встановлена потужність системи й знижується
ККД.
2.2 Паралельний інвертор з індуктивним регулятором
Фазовий метод стабілізації вихідної напруги паралельного інвертора може
бути реалізований за рахунок регулювання реактивної потужності комутуючого
конденсатора. Найбільш ефективно це можна здійснити за допомогою
регульованої індуктивності, наприклад, реактора з підмагнічуванням або
тиристорно- індуктивного регулятора. Структура подібної системи показана на
рис.2.4, а на рис. 2.5 представлені розгортки процесів, що пояснюють роботу
індуктивного регулятора.
При зміні кута регулювання тиристорів регулятора від 180º до 90º, можна
змінювати струм регулятора від 0 до деякого максимального значення,
обумовленого очевидним співвідношенням:
PP
)(
ПР)(LP
L
U
L
U
I
2
12
1
, (2.5)
де
ПР)(LP
I
1
– діюче значення першої гармоніки струму індуктивності регулятора
при
2
.
13
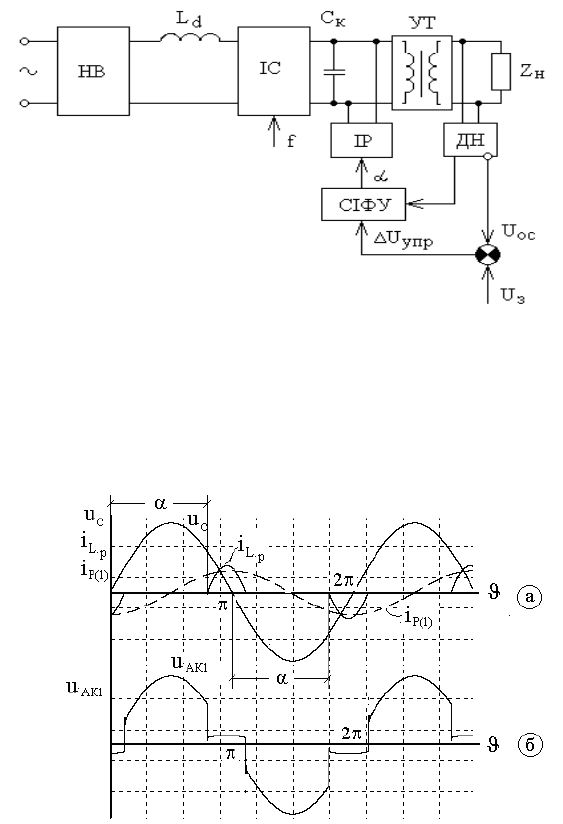
Рисунок 2.4 – Система з індуктивним регулятором
Рисунок 2.5 – Розгортки процесів в індуктивному регуляторі
Характерним є те, що кути регулювання менше, ніж 90 ел. градусів
реалізувати неможливо, тому що при зустрічно-паралельному включенні
тиристорів регулятора наступний тиристор може бути включений тільки після
вимикання тиристора, що раніше працював, а один з тиристорів регулятора
завжди включений, тому що струм індуктивності регулятора зміщений по фазі
стосовно вихідної напруги інвертора на 90 ел. градусів. Важливою властивістю
індуктивного регулятора, (визначає саму назву системи) є те, що перша гармоніка
струму регулятора Ip(1) , незалежно від величини кута , завжди зміщена на 90 ел.
градусів стосовно вихідної напруги, тобто має індуктивний характер.
На рис.2.5,б показана крива напруги між анодом і катодом тиристора
регулятора. Як видно з наведеної розгортки, у цій схемі на тиристорі пряма
напруга наростає зі швидкістю, обумовленою наростанням зворотної напруги на
14
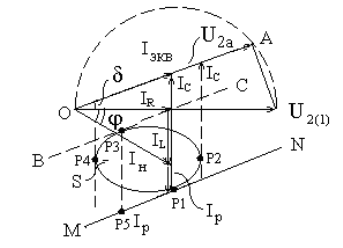
вийшовшому з роботи пристрої. Як правило, ця швидкість перевищує припустиму
величину навіть в приладах середньої потужності. Тому в реальній схемі
тиристори повинні бути шунтновані RС-ланцюгом, параметри якого слід
вибирати з умови обмеження .
Розрахунок інвертора з індуктивним регулятором зручно виконати,
використовуючи метод геометричних місць. Для цього будуємо векторну
діаграму, як показано на рис. 2.6, зважаючи, що U2=const. Як і в попередньому
випадку, область існування струму навантаження позначене як S. У цьому
випадку струм ємності Ic не змінюється, і для підтримки кута δ постійним
необхідно, щоб кінець вектора струму Ic сковзав по вектору струму Іекв. Отже,
геометричним місцем крапок початку вектора струму Ic повинна бути пряма MN,
паралельна вектору струму Іекв. Для забезпечення комутаційної стійкості
інвертора лінія MN повинна проходити нижче області існування струму
навантаження.
Рисунок 2.6 – Векторна діаграма інвертора з індуктивним регулятором
Для того, щоб вихідна напруга залишалася незмінною при всіх значеннях
струму навантаження, струм регулятора повинен бути таким, щоб початок
вектора струму Іс розміщувався на прямій MN. Ця умова реалізується за
допомогою системи авторегулювання, яка виробляє відповідні кути регулювання
тиристорів індуктивного регулятора.
Аналіз векторної діаграми дозволяє виділити деякі характерні режими
роботи системи. Наприклад, крапка Р1 на лінії MN, відповідна до крапки
перетинання вектора струму індуктивного регулятор з лінією MN, дозволяє
розрахувати величину струму індуктивного регулятора для заданого значення
15
величини й фази струму навантаження. Відповідно, крапка Р2 визначає режим
максимальної потужності в навантаженні, причому саме в цьому режимі найбільш
навантажені елементи схеми перетворювача. Крапка Р3 дозволяє визначити
граничну величину струму індуктивного регулятора, крапка Р4 корисна для
розрахунків мінімальних струмів в інверторі, при яких можливий вихід
випрямляча в режим переривчастого струму.
Недоліками розглянутої системи є неможливість реалізації рекуперативного
режиму й більш складна (у порівнянні із системою зі зворотним випрямлячем)
система керування, що вимагає наявності датчиків величини вихідної напруги
відповідного регулятора, і тому подібних елементів, характерних для будь-якої
системи авторегулювання.
У той же час, така система дозволяє забезпечити більш високу якість
стабілізації вихідної напруги, ніж, наприклад, система зі зворотним випрямлячем,
яка є системою параметричною. [3]
16
3 РОЗРАХУНОК І ВИБІР ВАРІАНТА
Випрямляч буде виконаний по однофазній мостовій схемі. Застосуємо
інвертор струму, виконаний по однофазній мостовій схемі, так як по завданню
форма вихідної напруги має бути близька до синусоїдальної. Регулювання струму
навантаження буде коливатися від мінімального до максимального значення.
Щоб вибрати спосіб регулювання вихідної напруги, треба виконати
розрахунок обох варіантів. А потім по єкономічним і масогабаритним показникам
вибрати найприбутковіший.
Початкові дані в таблиці 1.
Таблиця 1
m1 f1, Гц U1, B m2 f2, Гц U2,
B
I2, A cosφ2(1) Kнс
1 400 115 1 2500 460 10 – 20 0,1 – 0,3
84º - 73º
0,1
Максимальний коефіцієнт перетворення керованого випрямляча,
відповідний куту α = 0, необхідний при найменшій напрузі мережі живлення і при
мінімальному куті запасу δmin інвертора.
Тоді
),(5,88)05,01()1,01(1159,0)1()1()1(
*
11
*
)(0)(
ВUUUкUEU
xпxdd
де
)(d
U
– середнє значення випрямленної напруги, відповідне мінімально
допустимій величині напруги мережі живлення;
)(0 d
E
– середнє значення ЕРС холостого ходу випрямляча при мінімальній напрузі
мережі живлення;
1
U
– відносна величина відхилення напруги мережі живлення;
1
U
– номінальна напруга мережі живлення;
*
x
U
– відносна величина комутаційного падіння напруги, що приймається в
орієнтовних розрахунках рівної 0,05.
17

Мінімальний кут запасу для нормальної роботи інвертора:
,72)(25,110402250022
06
2min
радtfК
виклз
де
2
f
– частота на виході інвертора, Гц;
Кз =2 – коефіцієнт запасу;
викл
t
– час вимикання тиристорів, с.
Фазна напруга ( діюче значення першої гармоніки) на виході інвертора:
).(3,318
309,09,0
5,88
cos9,0cos
min
)(
min
)(
'
2
В
U
к
U
U
d
п
d
Знаходимо коефіцієнт трансформації
,44,1
3,318
460
'
2
2
U
U
К
Т
де
'
2
U
– фазна напруга на виході інвертора, В;
2
U
– фазна напруга на навантаженні, В.
Приведений до первинної сторони струм навантаження
).(292044,1
max2
max
'
2
АIКI
Т
)(4,141044,1
min
2
min
'
2
АIКI
Т
Необхідний струм ємності:
).(6,37)07,39,9(1,029)(cos
minmax2max2
'
2
АtgtgII
c
де
max2
cos
– мінімальний коефіцієнт потужності навантаження.
З векторної діаграми знаходимо найбільше значення вхідного інверторного
струму:
).(16,13)956,0296,37()3,029()sin()cos(
222
min2
/
2
2
min2
/
2
АIIII
cЭ
Середнє значення струму, що споживає інвертор від випрямляча:
).(76,1416,13
22
АIkI
эd
18
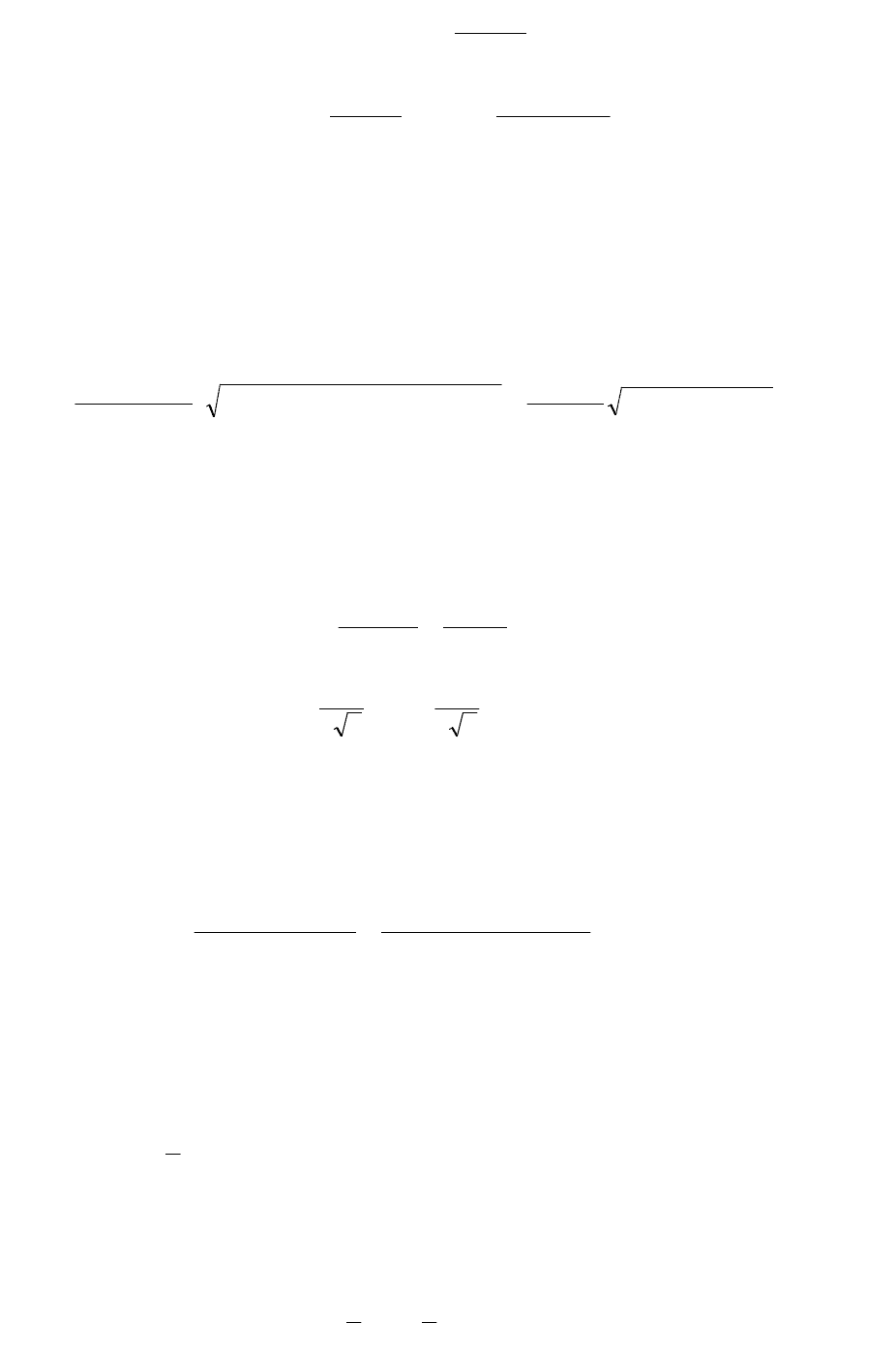
Для розрахунку згладжувального дроселя необхідно знайти амплітуду
першої гармоніки пульсацій на виході випрямляча при α= αmax.
R
LC
I
II
tg
max
о
R
LC
arctg
I
II
arctg 7,79)
32,4
77,136,37
()(
max
).(32,43,04,14cos
min2
/
min2
АII
R
).(77,13956,04,14sin
min2
/
min2
АII
L
В цьому випадку:
)(6,116968,04032,0
12
5,882
sin)(cos
1)(
2
2
max
22
11max
2
2
)(
)1(
Bmq
qm
qmU
U
d
m
Струм Id повинен відповідати режиму холостого ходу інвертора. При
холостому ході єквіваленнтний інверторний струм рівний струму ємності:
)(16,24
1788,0
32,4
cos
max
A
I
I
R
хх
экв
)(2716,24
22
14,3
22
AII
хх
эквdхх
Задаючись коефіцієнтом пульсацій струму Id близько 0,1, можна знайти
індуктивність згладжувального реактора:
).(106,8
271,0400214,32
6,116
3
)1(
Гн
IKmq
U
L
dxxn
m
d
Маса реактора визначається величиною L·I2, встановлену потужність
дроселя можно оцінити, розрахувавши реактивну потужність дроселя на частоті
400 Гц:
).(10276,14106,840014,325,0
2
1
3232
ВАрILS
ddLd
Середнє значення струму вентилів у випрямлячі і в інверторі однаково, так
як число фаз на вході і виході перетворювача однакове (m1=m2):
)(38,776,14
2
1
2
1
АII
d
вип
а
19

)(38,776,14
2
1
2
1
АII
d
інв
а
Зазвичай коефіцієнт використання вентилів по струму близько 0,5 – 0,6.
Отже, орієнтування можна вибрати вентилі на номінальний струм 15 А. Робоча
повторна напруга на вентилях також вибираеться із запасом не менше чим 1,3 –
1,5 на комутаційні перенапруження. Тоді напруга у випрямлячі:
)(06,313
8,0
4,11,11152
8,0
4,11,12
8,0
1,14,1
1
max
В
U
U
U
вип
b
вип
bррас
В інверторі:
)(5,866
8,0
4,11,13,3182
8,0
4,11,12
8,0
1,14,1
1
max
В
U
U
U
інв
b
інв
bррас
Таким чином, у випрямлячі слід поставити вентилі 5-го класу, а в інверторі
10-го, тобто UR RM(випр)=500 В, UR RM(інв)=1000 В.
Встановлена потужність вентилів відповідно:
)(1030500154
3
)()(
ABUInS
випRRMaнновипв
,
)(10601000154
3
)()(
ABUInS
інвRRMaнноінвв
Встановлена потужність конденсаторної батареї:
)(1096,116,373,3181
3'
22
ApBIUmQ
c
.
Встановлена потужність трансформатора:
).(102,9204601
3
222
ABIUmS
T
Таким чином, отримані параметри основних комплектуючих виробів,
необхідних для реалізації варіанту №1.
Розрахунок для варіанту №2.
)1()1(9.0)1(
*
11
*
)(0)( xxdd
UUUUEU
)(16,108)05,01()1,01(1159,0 B
Напруга на первинній обмотці трансформатора:
).(9,388
309.09,0
16,108
cos9,0
min
)(
'
2
B
U
U
d
Коефіцієнт трансформації:
183,1
9,388
460
'
2
2
U
U
К
Т
20
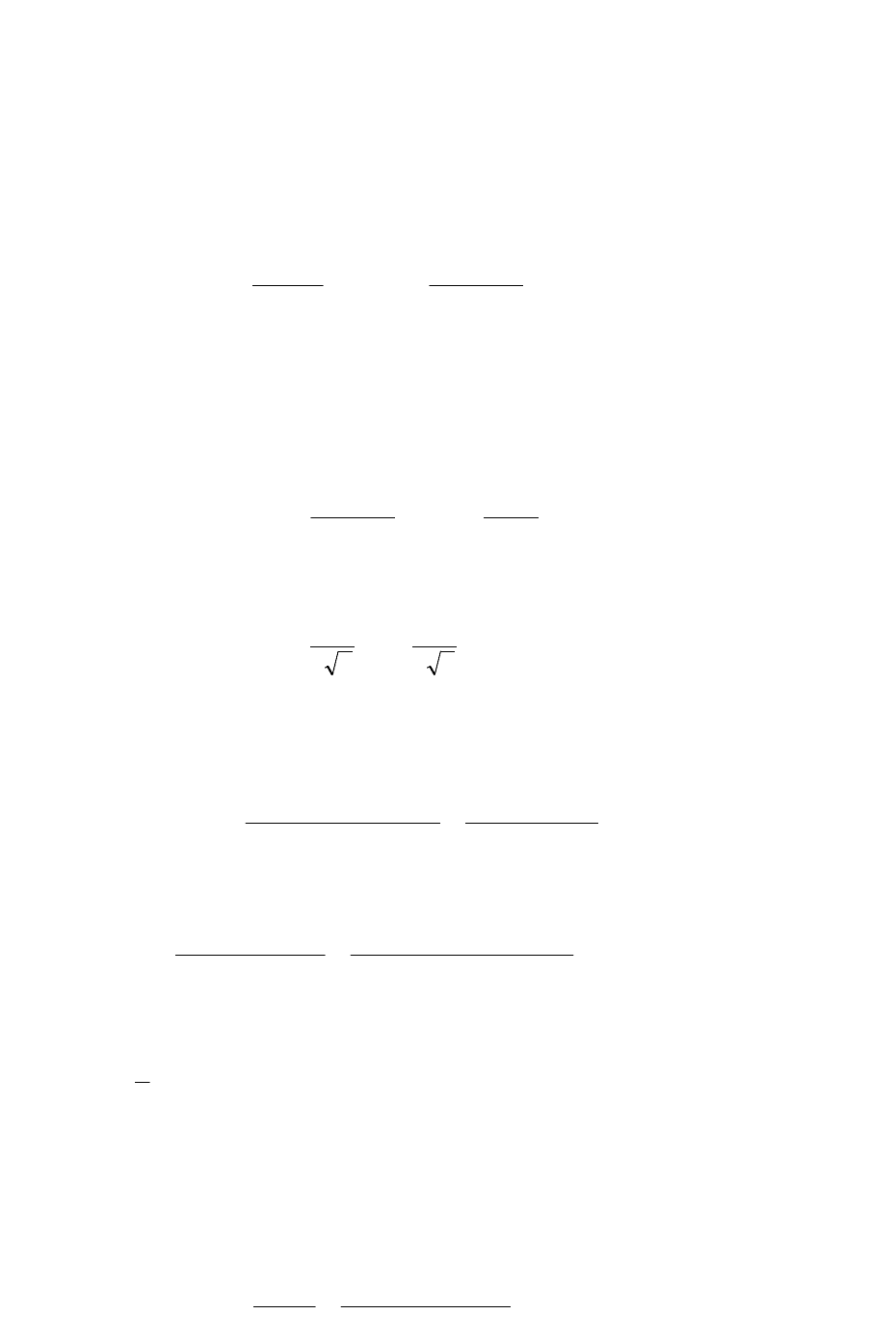
Приведений до первинної обмотки струм:
).(83,1110183,1
2
'
min2
AIКI
Т
).(66,2320183,1
2
'
max2
AIКI
Т
Напруга на вході інвертора при зниженні напруги мережі живлення:
).(5,88)05,01()1,01(1159.0)1()1()1(
*
11
*
)(0)(
ВUUUкUEU
xпxdd
Потрібний для стабілізації вихідної напруги кут:
.4,14252,0
9,3889,0
5,88
arccos
9,0
arccos
'
2
)(
)(
градрад
U
U
d
Струм ємності:
).(03,24)26,09,9(1,066,23)(cos
maxmax2max2
'
2
AtgtgII
c
Еквивалентний інверторний струм:
).(46,7
952.0
3,0
66,23
cos
cos
)(
min2
'
2
AII
э
Струм віпрямляча:
).(36,846,7
22
14,3
22
AII
эd
Амплітуда першої гармоніки пульсацій на виході некерованого випрямляча:
).(9,75
14
1,11159,02
1)(
)1(9,02
2
*
11
)1(
B
qm
UU
U
m
Індуктивність згладжувального дроселя:
).(1007,18
36,81,0400214,32
9,75
3
)1(
Гн
IКmq
U
L
dп
m
d
Встановлена потужність дроселя:
).(106,1)36,8(1007,1840014,325,0
2
1
323
2
АрВILS
ddLd
Максимальна величина струму індуктивного регулятора:
)(53,1)27,307,3(3,083,1103,24))()(()cos(
min2minmin22max
АtgtgIII
cp
Індуктивність реакторів регулятора:
).(1019,16
53,1250014,32
9,388
3
2
'
2
Гн
I
U
L
c
рег
21
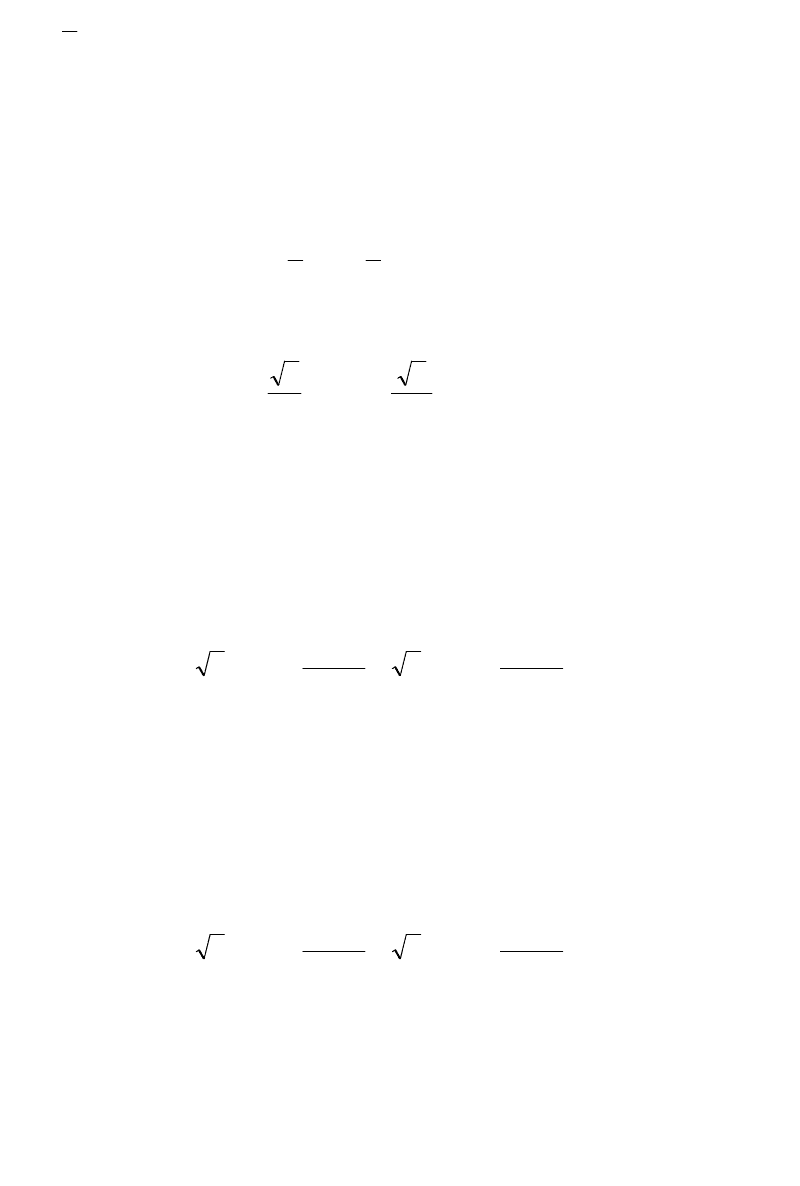
Встановлена потужність реакторів (у схемі їх три):
).(106,47)53,1(1019,1640014,325,0
2
1
323
2
max
АВILS
ррLp
Потужність конденсаторної батареї:
).(1034,903,249,388
3'
2
АВIUQ
c
Середнє значення анодного струму вентилів випрямляча і інвертора:
).(18,436,8
2
1
2
1
АII
da
Середнє значення струму вентилів регулятора:
).(69,053,1
14,3
22
max
АII
paр
Усі вентилі можуть, бути вибрані так само як у варіанті №1, на струм 15 А.
Амплітуда зворотньої напруги на вентилях випрямляча, їх встановлена
потужність озраховується так само, як у варіанті №1.
Амплітуда зворотньої напруги на вентилях інвертора:
).(7,1058
8,0
1,14,1
9,3882
8,0
1,14,1
2
'
2)max(
ВUU
линінвb
Вибираючи вентилі 12-го класу, матимемо встановлену потужність вентилів
в інверторі:
).(10721200154
3
)()(
АВUInS
інвRRMaнноінвв
Аналогічно, для регулятора:
).(7,1058
8,0
1,14,1
9,3882
8,0
1,14,1
2
'
2)max(
ВUU
линінвb
Вибираючи вентилі 12-го класу, матимемо встановлену потужність вентилів
регулятора:
).(10721200154
3
)()(
АВUInS
інвRRMaннорегв
Потужність вихідного трансформатора в обох варіантах однакова, оскільки
трансформатори відрізняються лише коефіцієнтом трансформації.
Для зіставлення варіантів результати розрахунку встановлених потужностей
заносяться в таблицю, куди також поміщають розрахунки маси, габаритних
розмірів або вартості вузлів, обчислених через вагові коефіцієнти,як в таблиці 2.
22
