Курсовая работа - Сравнительный анализ метода Шелла и метода Бэтчера по критерию эффективности

Подождите немного. Документ загружается.

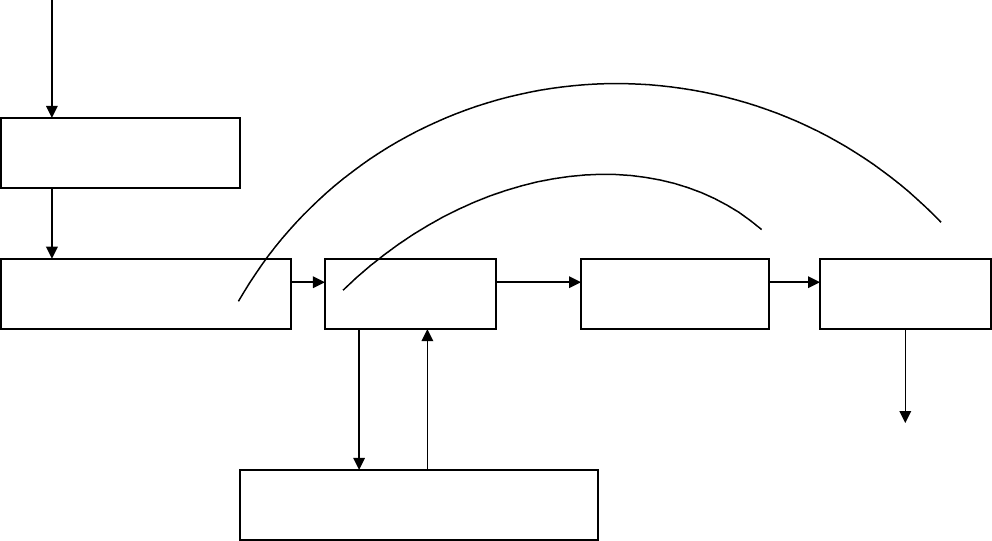
Схема сортировки Бэтчера несколько напоминает сортировку Шелла,

но сравнения выполняются по-новому, а потому цепочки операций обмена

записей не возникает. Поскольку в алгоритме Бэтчера, по существу,

происходит слияние пар рассортированных подпоследовательностей, его

можно назвать обменной сортировкой.

Алгоритм М (Обменная сортировка со слиянием). Записи R

, …,R

перекомпоновываются в пределах того же пространства в памяти. После

завершения сортировки их ключи будут упорядочены: K

<=…<=K

Предполагается, что N >=2 (рис. 1).

Рис. 1 Схема сортировки метода Бэтчера

М1. [Начальная установка p] Установить p ← 2

t –1

, где t=[lg N] –

наименьшее целое число, такое, что 2

N. (Шаги M2-M5 будут выполняться

с p = 2

t-1

t-2

,…,1)

M2.

[Начальная установка q, p, d.] Установить q2

t-1

, r0, dp.

M1. Нач. установка

M2. Нач. установка q, r, d M3. Цикл по

M5. Цикл по q M6. Цикл по

i>=N-d q=p

p=0

M4. Сравнение/обмен R

i+1

: R

i+d+1

0<= i <N-d

i ∧ p=r

M3. [Цикл по i] Для всех I, таких, что 0I<N-d и iΛp=r, выполнить шаг

М4. Затем перейти к шагу М5. (Здесь через iΛp обозначена операция

«поразрядное логическое И» над представлениями целых чисел i и p; все

биты результата равны 0, кроме тех битов, для которых в соответствующих

разрядах i и p находятся 1. Так, 13Λ21=(1101)

Λ(10101)

=(00101)

=5. К этому

моменту d –нечетное кратное p (т.е. частное от деления d на p нечетно), а p –

степень двойки, так что iΛ p (I+d) Λ p. Отсюда следует, что шаг М4 можно

выполнять при всех нужных значениях i в любом порядке или даже

одновременно.)

M4. [сравнение/обмен R

i+1

: R

i+d+1

.] Если

Ki+1

>Ki

+d+1

, поменять местами

записи R

i+1

 R

i+d+1

M5. [Цикл по q] Если qp, установить d q-p, qq/2, rp и

возвратиться к шагу М3.

M6. [Цикл по p] (К этому моменту перестановка К

…К

будет p-

упорядочена.) Установить р[p/2]. Если р0, возвратиться к шагу М2.

В таблице этот метод проиллюстрирован при N=16. Обратим внимание

на то, что, по существу, алгоритм сортирует N элементов путем независимой

сортировки подмассивов R

,… и R

,…, после чего выполняются

шаги М2-М5 при р=1 для слияния двух рассортированных

последовательностей. Реализация данного алгоритма на языке

программирования Turbo Pascal 7.0 приведена в приложении 2.

Анализ сортировки Бэтчера.

Чтобы доказать, что магическая последовательность сравнений и/или

обменов, описанная в алгоритме М, действительно позволяет рассортировать

любую последовательность R

… R

, необходимо показать только, что в

результате выполнения шагов М2-М5 при р=1 будет слита любая 2-

упорядоченная последовательность R

… R

; каждая 2-упорядоченная

перестановка множества{1,2….,N} соответствует на решетке единственному

пути из вершины (0,0) к ([N/2],[N/2]). На рисунке 1, показан пример при

N=16, соответствующий перестановке 1 3 2 4 10 5 11 6 13 7 14 8 15 9 16 12.

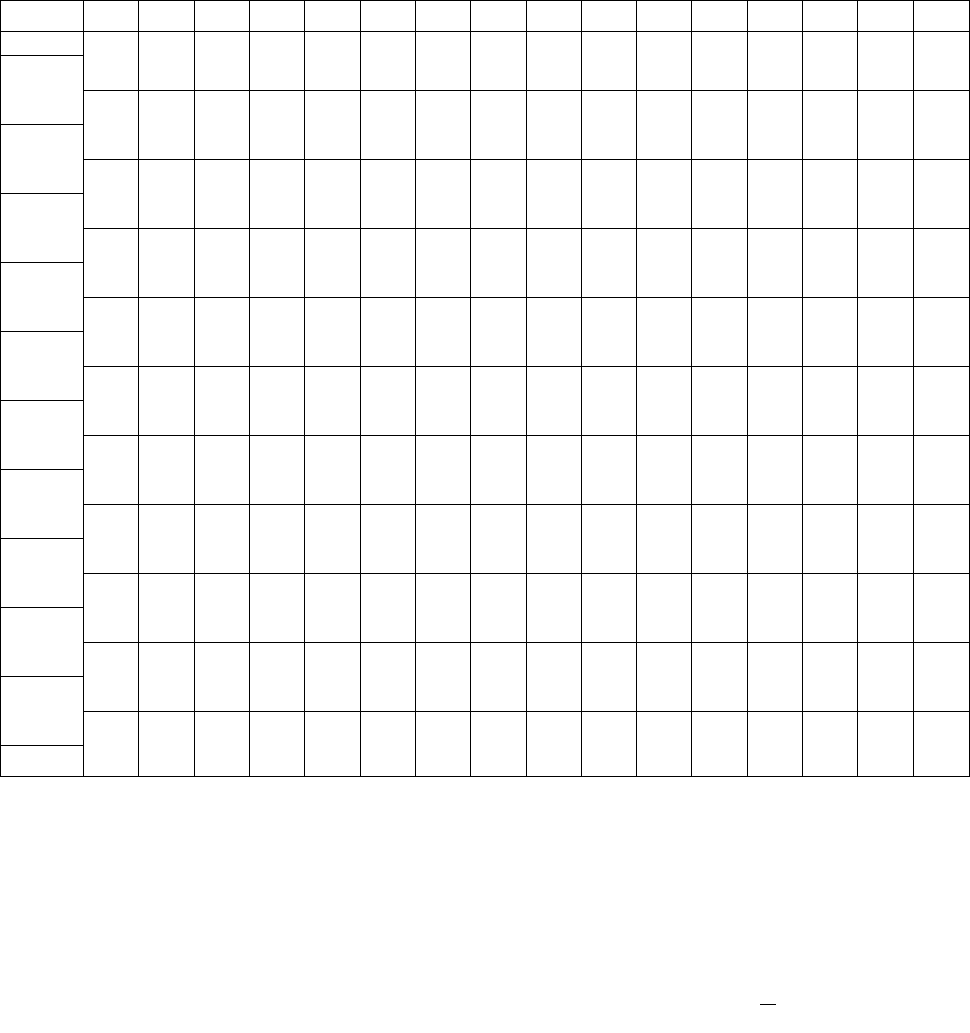
При р=1, q=2

t-1

, r=0, d=1 на шаге М3 выполняется сравнение (и, возможно,

обмен) записей R

: R

, R

: R

и т.д. Этой операции соответствует простое

преобразование пути на решетке:

Таблица 1

Обменная сортировка со слиянием (Метод Бэтчера)

P q rd

503 087 512 061 908 170 897 275 653 426 154 509 612 677 765 703

8 8 08

503 087 154 061 612 170 765 275 653 426 512 509 908 677 897 703

4 8 04

503 087 154 061 612 170 765 275 653 426 512 509 908 677 897 703

4 4 44

503 087 154 061 612 170 512 275 653 426 795 509 908 677 897 703

2 8 02

154 061 503 087 512 170 612 275 653 426 765 509 897 677 908 703

2 4 26

154 061 503 087 512 170 612 275 653 426 765 509 897 677 908 703

2 2 22

154 061 503 087 512 170 612 275 653 426 765 509 897 677 908 703

1 8 01

061 154 087 503 170 512 275 612 426 653 509 765 677 897 703 908

1 4 17

061 154 087 503 170 512 275 612 426 653 509 765 677 897 703 908

1 2 13

061 154 087 275 170 426 503 509 512 653 612 703 677 897 765 908

1 1 11

061 087 154 170 275 426 503 509 512 612 653 677 703 765 897 908

На следующей итерации М3 имеем p=r=1 и d=2

t-1

-1,2

t-2

-1,…,1. В

результате произойдет сравнение и/или обмен записей R

: R

2+d

, R

: R

4+d

и т.д.

Опять же, имеется простая геометрическая интерпретация: путь

«перегибается» относительно прямой, расположенной на

 

d

единиц

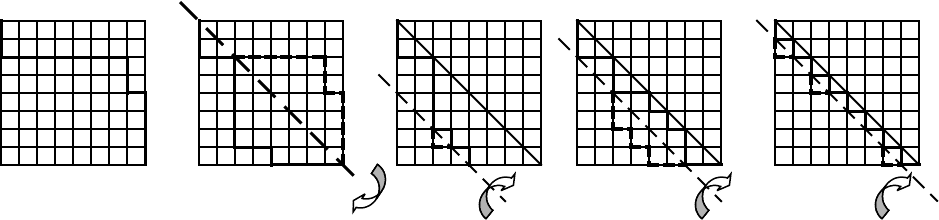
ниже диагонали. В конце концов, получаем путь, который соответствует

полностью рассортированной перестановке. На этом «геометрическое

доказательство» справедливости алгоритма Бэтчера завершается (данный

алгоритм можно было бы назвать сортировкой посредством перегибов).

Однако, она обладает одним важным компенсирующим качеством: все

сравнения и/или обмены, определяемые данной итерацией шага М3, можно

выполнять одновременно на компьютерах или в сетях, которые реализуют

параллельные вычисления. С такими параллельными операциями сортировка

осуществляется за ½ [lgN] ([lgN]+1) шагов, и это один из самых быстрых

общих методов среди всех известных. Например, 1024 элемента можно

рассортировать методом Бэтчера всего за 55 параллельных шагов. Его

ближайшим соперником является метод Пратта, который затрачивает 40 или

73 шага в зависимости от того, как считать: если допускать перекрытие

сравнений до тех пор, пока не требуется выполнять перекрывающиеся

обмены, то для сортировки 1024 элементов методом Пратта требуется всего

40 циклов сравнения и/или обмена.

(а) (б) (с) (d) (e)

Рис. 2 Геометрическая интерпретация метода Бэтчера

ГЛАВА 2 ИНСТРУМЕНТАРИЙ ИССЛЕДОВАНИЯ АЛГОРИТМОВ

СОРТИРОВКИ

2.1 Корреляционно – регрессионный анализ как основной

инструмент исследования алгоритмов

Корреляционно-регрессионный анализ проверяет наличие и значимость

линейной зависимости между переменными без указания зависимой и

объясняемых переменных.

Пользуясь методами корреляционно - регрессионного анализа, анали-

тики измеряют тесноту связей различных показателей с помощью

вычисленного для них коэффициента корреляции. При этом обнаруживаются

связи, различающиеся по силе (сильные, слабые, умеренные и др.) и по

направлению (прямые, обратные). Если связи окажутся существенными, то

целесообразно будет найти их математическое выражение в виде

регрессионной модели и оценить статистическую значимость модели. Если в

результате исследования получится значимое уравнение, то его можно

использовать для прогнозирования или анализа изучаемого явления или

показателя.

Корреляционно-регрессионный анализ связей между переменными

показывает, как один набор переменных (X) может влиять на другой набор

(Y). Таким образом, регрессионные вычисления и подбор хороших

уравнений - это ценный, универсальный исследовательский инструмент в

самых разнообразных отраслях деловой и научной деятельности (маркетинг,

торговля, медицина, социология, исследования алгоритмов и т.д.).

Во всех перечисленных областях широко применяются как

однофакторные, так и множественные регрессионные модели.

Корреляционно-регрессионный анализ считается одним из главных методов

в различных исследованиях, наряду с оптимизационными расчетами, а также

математическим и графическим моделированием прогнозируемых явлений с

помощью трендов. Для более полного представления процесса построения

многофакторных регрессионных моделей рассмотрим этапы проведения

корреляционно – регрессионного анализа.

Нулевой этап - это сбор данных. Огромное внимание на данном этапе

уделяется качеству данных. Сбор данных создает фундамент прогнозам.

Поэтому имеется ряд требований и правил, которые следует соблюдать при

сборе данных. Основное из этих требований – это для построения

регрессионной модели желательно использовать статистические данные по

результатам независимых испытаний, проводимых в рамках исследования.

Первый этап - корреляционный анализ. Его цель - определить характер

связи (прямая, обратная) и силу связи (связь отсутствует, связь слабая,

умеренная, заметная, сильная, весьма сильная, полная связь). Корре-

ляционный анализ создает информацию о характере и степени выраженности

связи (коэффициент корреляции), которая используется для отбора

существенных факторов, а также для планирования эффективной последо-

вательности расчета параметров регрессионных уравнений. При одном

факторе - вычисляют коэффициент корреляции, а при наличии нескольких

факторов - строят корреляционную матрицу, из которой выясняют два вида

связей: связи зависимой переменной с независимыми, связи между самими

независимыми переменными.

Второй этап - расчет параметров и построение регрессионных моделей.

Здесь стремятся отыскать наиболее точную меру выявленной связи, для того

чтобы можно было прогнозировать, предсказывать значения зависимой

величины Y, если будут известны значения независимых величин Х1, Х2, …,

Хn. Эту меру обобщенно выражают математической моделью линейной

множественной регрессионной зависимости: у = а0 + b1x1 + b2x2 + … +

bnxn.

После получения каждого варианта уравнения обязательной

процедурой является оценка его статистической значимости, поскольку

главная цель – получить уравнение наивысшей значимости, поэтому второй

этап корреляционно-регрессионного анализа неразрывно связан с третьим.

На третьем этапе выясняют статистическую значимость, т. е. при-

годность постулируемой модели для использования ее в целях предсказания

значений отклика. На этом этапе исключительно важную роль играют коэф-

фициент детерминации и F - критерий значимости регрессии. R Squared (R2)

- коэффициент детерминации - это квадрат множественного коэффициента

корреляции между наблюдаемым значением Y и его теоретическим

значением, вычисленным на основе модели с определенным набором

факторов. Коэффициент детерминации измеряет действительность модели.

Он может принимать значения от 0 до 1. Эта величина особенно полезна для

сравнения ряда различных моделей и выбора наилучшей модели.

На четвертом этапе корреляционно-регрессионного исследования, если

полученная модель статистически значима, ее применяют для прогно-

зирования (предсказания), управления или объяснения. Если же обнаружена

незначимость, то модель отвергают, предполагая, что истинной окажется

какая-то другая форма связи, которую надо поискать. Незначимость ее

служит основанием для того, чтобы отвергнуть только линейную форму

модели. Возможно, что более подходящей будет нелинейная форма модели.

Для определённости эндогенные переменные в этих моделях будем

называть результативными признаками, а экзогенные переменные будем

называть факторными признаками. Построенная регрессионная

эконометрическая модель позволит: во-первых, определить математическую

зависимость между переменными, во-вторых, измерить тесноту связи между

ними, в-третьих, проанализировать влияние отдельных факторных признаков

на результат.

Постановка задачи регрессионного анализа:

1. Прежде всего, следует выбрать показатель, отражающий результаты

исследований, анализ которых выполняется. Выбранное направление, тема

анализа могут характеризоваться целым рядом показателей результатов

эффективности исследования. Например, по теме «время выполнения

алгоритма» такими характеристиками могут быть время, затрачиваемое на

количество сравнений, время, требующееся на количество перестановок,

время, необходимое на считывание сортируемых элементов с внешнего

носителя, технические характеристики компьютера и др. Из них нужно

выбрать показатель, в наибольшей степени отвечающий целям и задачам

исследования. Можно построить несколько уравнений регрессии с

различными показателями результатов исследования.

2. После выбора результирующего показателя определяются факторы,

на него влияющие. Этот этап во многом определяет результат работы.

Отметим, что при выборе факторов для уравнения регрессии полезно

использовать методы системного анализа, в частности построение дерева

целей. В этом случае поставленная проблема, выбранная цель

детализируются постепенно по ряду направлений и представляются в виде

взаимосвязанных проблем, подцелей, влияющих на достижение общей цели.

3. После определения показателя результатов исследования и факторов

собираются статистические данные по ним. Они могут быть получены путем:

а) временной (фиксируется объект наблюдений, и собираются данные

за ряд периодов времени).

б) пространственной выборки (фиксируется период времени и

собираются статистические данные по ряду объектов: массивам, спискам и т.

д. Возможна и комбинация этих способов сбора данных).

При исследовании корреляционной зависимости, прежде всего, должно

быть построено уравнение регрессии.

Уравнение регрессии - это модель, которая в численной форме

выражает зависимость показателя результатов деятельности от влияющих на

него факторов. Действие каждого фактора на результат не является строго

определенным, функциональным, оно изменяется в зависимости от времени,

условий исследования и проявляется лишь в массе случаев.

Парная корреляция. Простейший случай представляет собой парная

корреляция (простая линейная регрессия), где рассматривается зависимость

между двумя показателями: показателем результатов (у) и одним фактором

(х), от которого зависит этот показатель. Такие модели называют

однофакторными. Форма зависимости может быть линейной и нелинейной.

Нелинейность может проявляться как относительно факторов, так и

входящих в функцию коэффициентов. В различных исследованиях наиболее

часто встречаются шесть следующих формул:

y = a0 + a1x — линейная,

y = a0 + a1 / x — гиперболическая,

y = a0 + a1x + a2x2 — квадратичная,

y = a0 + a1x + a2x2 + … + anx2 — полином,

y = a0xa1 — степенная,

y = a0a1x — показательная,

y = ea1x — экспоненциальная.

Линейная функция (y = a0 + a1x) наиболее широко применяется в

описании различных процессов, хотя является лишь приближением к

реальным взаимосвязям, которые в силу своей сложности и

многофакторности бывают нелинейными. В зависимости от знака

коэффициента a1, который определяется в результате расчетов, влияние

фактора может быть прямым (при a1> 0) и обратным (при a1 < 0).

Исходным материалом для составления уравнения регрессии являются

значения показателей х и у по наблюдениям, т. е. имеется некоторая таблица,

в которой фактическим значениям х соответствуют фактические значения y,

другими словами, задана табличная функция. Восстановить функцию по

конечному числу ее значений - с математической точки зрения, задача

неразрешимая. Поэтому ставится задача заменить табличную функцию одной

из выше перечисленных формул так, чтобы значения ее как можно меньше

отличались от экспериментальных данных. Формула, полученная на

основании экспериментальных данных, называется эмпирической.

2.2 Табличный процессор MS Excel’ 2003 как основной инструмент

автоматизации процесса проведения регрессионного анализа данных

В русифицированной версии EXCEL для корреляционно-

регрессионного анализа используются средства специального статического

модуля. Microsoft заказывала разработку этого модуля фирме,

специализирующейся на программном обеспечении математико-статических

задач. Модуль включает в себя два вида средств математико-статического

анализа: функции и инструменты.

Статические функции, вызываются через окно Мастер функций.

Функция КОРРЕЛ (расчет корреляции между двумя множествами данных)

запрашивает два исходных множества (массива) данных и выдает

коэффициент корреляции в ту клетку, куда был установлен курсор перед

обращением к функции.

На окно мастера функций наложено окно самой функции КОРРЕЛ,

хотя на самом деле одновременный обзор этих двух окон исключен.

Множественный корреляционно-регрессионный анализ в основном

ориентирован на средства дополнительного пакета Анализ данных.

Активизация команды Сервис/Анализ данных открывает окно Инструменты

анализа, предоставляющие 19 статических инструментальных средств. Среди

них – Корреляция и Регрессия, непосредственно и эффективно

поддерживающие простой и множественный корреляционно-регрессионный

анализ.

При многофакторной модели табличный процессор облегчает работу,

связанную с расчётом коэффициентов регрессии, частных коэффициентов

эластичности, множественной корреляции и коэффициентов детерминации

(при этом можно использовать такие функции, как: МОБР, МОПРЕД,

МУМНОЖ, КОРЕНЬ и т.д.).