Курсовая работа - Определение емкости водохранилища. Построение кривых обеспеченности
Подождите немного. Документ загружается.


1.4 Характерные уровни и емкости водохранилища.
Основными характеристиками водохранилищ являются:
1) нормальный подпорный уровень НПУ, м;
2) уровень мёртвого объема УМО, м;
3) катастрофический подпорный уровень КПУ, м;
4) полный объем водохранилища W, млн. м
3
или км
3
;
5) полезный объем водохранилища W
плз
, млн. м
3
или км
3
;
6) мертвый объем водохранилища W
мо
, млн. м
3
или км
3
;
7) объем форсировки водохранилища W
фс
, млн. м
3
или км
3
;
8) коэффициент емкости водохранилища в= W
плз
/W
о
,
где W
о
– средний многолетний сток.
НПУ – уровень воды, до которого водохранилище заполняется в
нормальных условиях.
Полный объем водохранилища W – объм, заключенный между дном чаши
водохранилища и зеркалом воды на отметке НПУ. Полный объем W не
целиком используется для регулирования стока. Нижняя часть водохранилища,
предназначенная для поддержания минимальных уровней воды и осаждения в
ней наносов, называется мертвым объемом W
мо
и сработке не подлежит.
Объем водохранилища, заключенный между поверхностями воды на
отметках НПУ и УМО, называется полезным объемом — W
плз
. В периоды
многоводья он заполняется, а в периоды маловодья опорожняется. Объем,
заключенный между поверхностями воды на отметках НПУ и КПУ,
называется объемом форсировки. КПУ — катастрофически подпертый
уровень в период пропуска через гидроузел исключительно многоводных
половодий или паводков. Объем, форсировки W
фс
служит для уменьшения
величины сбросных расходов через гидроузел.
11

Образование водохранилища вызывает изменения в режиме водотока. В
верхнем бьефе эти изменения в основном сводятся к следующему:
1)повышаются уровни воды и увеличиваются глубины, что
связано с затоплением территории в пределах чаши водохранилища;
2)уменьшаются скорости течения, в результате чего происходит
выпадение значительной части осадков;
3)увеличивается водное зеркало, в связи с чем происходит увеличение
испарения, что ведет к повышению солености воды в водохранилище.
В нижнем бьефе происходят такие изменения: уменьшаются половодные и
паводковые расходы и увеличиваются меженние; и происходит размыв русла
ниже гидроузла. Кроме указанных изменений в водотоке в верхнем бьефе
происходят следующие: затопление территории в пределах чаши
водохранилища; подтопление прилегающих к водохранилищу земель и
обрушение берегов водохранилища под воздействием волн.
Рисунок 2. Основные элементы водохранилища
12

Кроме постоянного затопления земель, занятых водохранилищем в
пределах НПУ, хозяйственное использование которых невозможно,
наблюдаются временные затопления территории выше НПУ во время
катастрофических половодий и паводков, от нагона воды ветром на берега и
от подъема уровней воды при заторах и зажорах. Хозяйственное
использование временно затопляемых земель возможно. При подтоплении
происходит подъем грунтовых вод, что резко ухудшает условия
хозяйственного использования земель и требует осушительных
мероприятий.
Характерные уровни воды и их отметки находим, используя
топографические характеристики водохранилища:
- НПУ, соответствующий наполнению W
полн
= 10.326 млн. м
3
, на отметке
НПУ = 131.8 м плотины равен
НПУ =
НПУ -
ПП = 131.8 – 120.0 = 11.8 м;
- уровень мертвого объема на отметке
УМО = 121.2 м равен
УМО =
УМО -
ПП = 121.2 – 120.0 = 1.2 м;
- форсированный подпорный уровень ФПУ равен
ФПУ = НПУ + 2.0 = 13.8 м,
где
ПП – отметка подошвы плотины.
13

2. Построение кривых обеспеченности
2.1 Обеспеченность гидрологических характеристик
Колебания стоковых характеристик не являются функцией времени
и не имеют определенных закономерностей, поэтому по имеющимся
данным наблюдений за элементами гидрологического режима
невозможно установить хронологический ход стока на будущий
запланированный период. Невозможно и определить, когда будет
наблюдаться какое-либо значение характеристики стока и сколько раз
за это время рассматриваемая характеристика стока превысит то или
иное значение. На современном этапе знаний предстоящий сток
приходится описывать в виде вероятностно-количественной оценки,
отвечающей той или иной повторяемости или обеспеченности
исследуемой характеристики.
Исходные данные – календарный ряд наблюдений (расходов за n
лет). Расходы располагают не в календарной последовательности, а в
порядке убывания.
Разность между наибольшим (х
тах
) и наименьшим (х
тin
) значениями в
ряду по убыванию представляет амплитуду или варьирование величин в
ряду. Общую амплитуду колебания исследуемой случайной величины
(среднего годового расхода) можно разделить на отдельные интервалы, или
градации, число которых обычно назначается в зависимости от объема
14
рассматриваемого материала так, чтобы отразить типичные черты
рассматриваемого ряда наблюдений.
Для приближенной оценки числа интервалов Можно использовать
эмпирические формулы, например n
х
≤5lg∙n,
где n
х
— число интервалов; n — общее число наблюдений.
После назначения интервалов (градаций) подсчитывается число
попаданий случайной величины (среднего годового расхода) в каждый
интервал, при этом сумма случаев по всем градациям равна общему числу
лет наблюдений n. Число величин в каждом интервале называют абсолютной
частотой. Выражая абсолютные частоты в процентах от общего числа
случаев, получают относительные частоты. Сумма относительных частот
равна 100%. Абсолютная и относительная частоты представляют
повторяемость величин, попадающих в данный интервал. По значениям
относительных частот можно построить график, на котором по оси ординат
отложены градации расходов, а по оси абсцисс— в виде прямоугольников
относительные частоты.
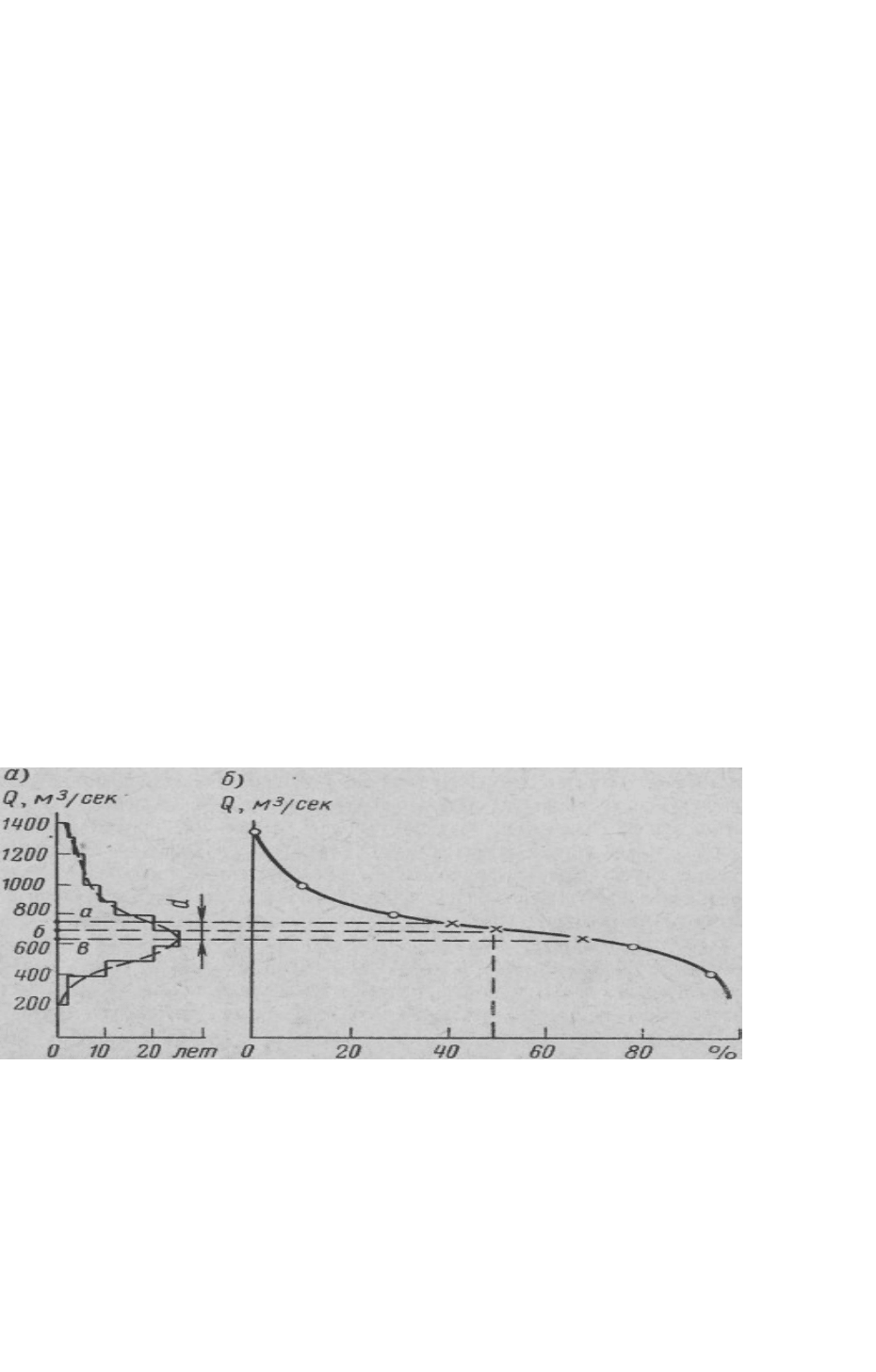
Рисунок 3 Схема построения по кривой распределения вероятностей (а) кривой обеспеченности (б)
Полученный график относительных частот называют гистограммой
распределения. При бесконечном увеличении числа интервалов с
бесконечным уменьшением каждого интервала ступенчатая гистограмма
распределения превращается в плавную кривую распределения вероятно-
стей, которую называют кривой повторяемости. Эта кривая дает
15
наглядное представление о законе распределения случайной вели чины и
показывает частоту или повторяемость того или иного значения
случайной величины.
Последовательным суммированием относительных частот в пределах
выделенных интервалов начиная от наибольшего значения получают
суммарную (интегральную) кривую распределения вероятностей, которую
называют кривой обеспеченности (рис. 5 б). Кривая обеспеченности – это
интегральная кривая, показывающая обеспеченность или вероятность
превышения в % или долях от единицы данной величины среди общей
совокупности ряда.
2.2 Построение эмпирической кривой обеспеченности
При наличии ряда наблюдении порядка 20 и более лет построение кривой обеспеченности
выполняется с помощью таблицы вспомогательных величин (табл.4).
Годы Q
№
m
Расходы в
убывающем
порядке
K - 1
(K – 1)
2
P
1971 1770 1 2160 1.27 0.0729 3.27
1972 1790 2 2120 1.24 0.0576 7.94
1973 1180 3 2090 1.22 0.0484 12.62
1974 1790 4 2050 1.20 0.0400 17.29
1975 2120 5 2000 1.17 0.0289 21.96
1976 1480 6 1980 1.16 0.0256 26.64
1977 1870 7 1870 1.10 0.0100 31.31
1978 1850 8 1850 1.08 0.0064 35.98
1979 1250 9 1790 1.05 0.0025 40.65
1980 1230 10 1790 1.05 0.0025 45.33
1981 2160 11 1770 1.04 0.0016 50.00
1982 1710 12 1760 1.03 0.0009 54.67
1983 1620 13 1710 0 0 59.35
1984 2090 14 1620 -0.05 0.0025 64.02
1985 2050 15 1550 -0.09 0.0081 68.69
1986 1550 16 1480 -0.13 0.0169 73.36
1987 1220 17 1370 -0.20 0.0400 78.04
1988 2000 18 1250 -0.27 0.0729 82.71
1989 1370 18 1230 -0.28 0.0784 87.38
1990 1760 20 1220 -0.29 0.0841 92.06
1991 1980 21 1180 -0.31 0.0961 96.73
16

Табл.4
∑ 35840 +1.61 0.6963
-1.62
Q
ср
= 1706.67
В графе 6 подсчитывается обеспеченность полученного ряда в
процентах по формуле
P = m/(n+1)·100%
где m - порядковый номер члена ряда при расположении их в убывающем
порядке;
n - число членов в ряду.
Если сток за отдельные годы выразить в виде модульных коэффициентов:
К
i
=
Qñð
Q
i
, то
С
v
=
1
1
2
n
K
= 0.19,
С
v
– коэффициент вариации.
Относительная средняя квадратическая ошибка средней многолетней
величины годового стока реки за период с 1971 по 1991 гг. равна:
=
%100*
n
C
v
= 4.08 %.
≤15% - длина ряда достаточна.
17
2.3 Построение теоретической кривой по методу
Крицкого-Менкеля
В практике гидрологических расчетов из множества математических
кривых распределения наибольшее распространение получили биномиальная
кривая распределения (кривая Пирсона III- типа) и кривые
трехпараметрического гамма-распределения, разработанные С. Н. Крицким и М.
Ф. Менкелем. Наиболее удачную общую функцию распределения удалось по-
лучить С. Н. Крицкому и М. Ф. Менкелю.
Ординаты кривой определяем в зависимости от коэффициента С
v
по
таблицам, составленным С.Н. Крицким и М.Ф. Менкелем для C
s
=2С
v
. Для
повышения точности кривой необходимо учитывать сотые доли С
v
и провести
интерполяцию между соседними столбцами цифр.
Теоретические кривые обеспеченности в гидрологии наиболее
часто применяются для определения среднегодовых значений стока, а также
максимальных и минимальных расходов.
Кривые обеспеченности, построенные по изложенным выше методам
обычно имеют в своих верхних и нижних отрезках весьма крутой подъем и спад,
что затрудняет пользование ими в этих частях, и особенно их экстраполяцию.
Поэтому при построении кривой обеспеченности предложена особая клетчатка
вероятности, которая имеет равномерные деления вертикальной шкалы и
неравномерные горизонтальной. Она построена так, что кривая обеспеченности
при C
s
= 0 полностью спрямляется. Клетчатка вероятности бывает с обычной
шкалой и логарифмической — вертикальной.
18

19

Табл.5 Построение кривой обеспеченности по методу Крицкого-Менкеля
Р,
%
0.01 0.05 1 3 5 10 15 20 25 30 40 50
К
1.871 1.749 1.693 1.494 1.387 1.332 1.251 1.156 1.120 1.090 1.036 0.987
КQ
o
3193.18 2984.97 2889.39 2549.76 2367.15 2273.28 2135.04 1972.91 1911.47 1860.27 1768.11 1684.48
Продолжение табл.5
60 70 75 80 85 90 95 97 99 99.9
0.941 0.892 0.865 0.838 0.806 0.766 0.711 0.676 0.613 0.515
1605.98 1522.35 1476.27 1430.19 1375.58 1307.31 1213.44 1153.71 1046.19 878.94
20
