Курсовая работа - Некоторые уравнения математической физики в частных производных
Подождите немного. Документ загружается.


Так как иначе мы имели бы
T
(
t
)
≡0 и u
(
x, t
)
≡0,
в то время как задача состоит в нахождении нетривиального решения. Для
функции T (t) в основной вспомогательной задаче никаких дополнительных
условий нет.
Таким образом, в связи с нахождением функции X (x) мы приходим к
простейшей задаче о собственных значениях:
найти те значения параметра
λ
, при которых существуют нетривиальные
решения задачи:
X
' '
+λX =0,
¿
}
¿¿¿
(18)
а также найти эти решения. Такие значения параметра
λ
называются
собственными значениями, а соответствующие им нетривиальные решения –
собственными функциями задачи (18). Сформулированную таким образом
задачу часто называют задачей Штурма – Лиувилля.
Рассмотрим отдельно случаи, когда параметр
λ
отрицателен, равен нулю
или положителен.
1. При
λ
‹ 0 задача не имеет нетривиальных решений. Действительно,
общее решение уравнения (15) имеет вид
X ( x )=C
1
e
√
−λ x
+C
2
e
√
−λ x
.
Граничные условия дают:
Х (0) = С
1
+ С
2
= 0;
Χ
(
ℓ
)
=С
1
е
α
+С
2
е
−α
=0
(
α=ℓ
√
− λ
)
,
т. е.
С
1
=−С
2
и C
1
(
е
α
−е
−α
)
=0 .
Но в рассматриваемом случае
α
– действительно и положительно, так что
е
α
−е
−α
≠0
. Поэтому
С
1
=0, С
2
= 0
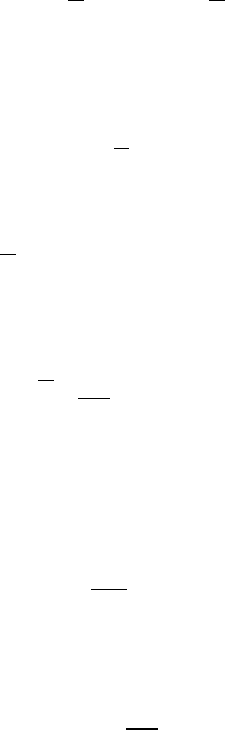
и, следовательно,
Х (х)
¿
0.
2. При
λ
= 0 также не существует нетривиальных решений.
Действительно, в этом случае общее решение уравнения (15) имеет вид
Х (х) = С
1
х + С
2
.
Граничные условия дают:
X (0)=
[
C
1
x+C
2
]
x =0
=C
2
=0,
X ( ℓ)=C
1
ℓ=0,
т. е. С
1
= 0 и С
2
= 0 и, следовательно,
Х (х)
¿
0.
3. При
λ
› 0 общее решение уравнения может быть записано в виде
X ( x )=D
1
cos
√
λ x+D
2
sin
√
λ x .
Граничные условия дают:
X (0)=D
1
=0,
X ( ℓ)=D
2
sin
√
λ ℓ=0.
Если Х(х) не равно тождественно нулю, то D
2
¿
0, поэтому
sin
√
λ ℓ=0
(19)
или
√
λ=
πn
ℓ
,
где n- любое целое число. Следовательно, нетривиальные решения задачи (18)
возможны лишь при значениях
λ=λ
n
=
(
πn
ℓ
)
2
.
Этим собственным значениям соответствуют собственные функции
X
n
( x )=D
n
sin
πn
ℓ
x ,
где D
n
– произвольная постоянная.
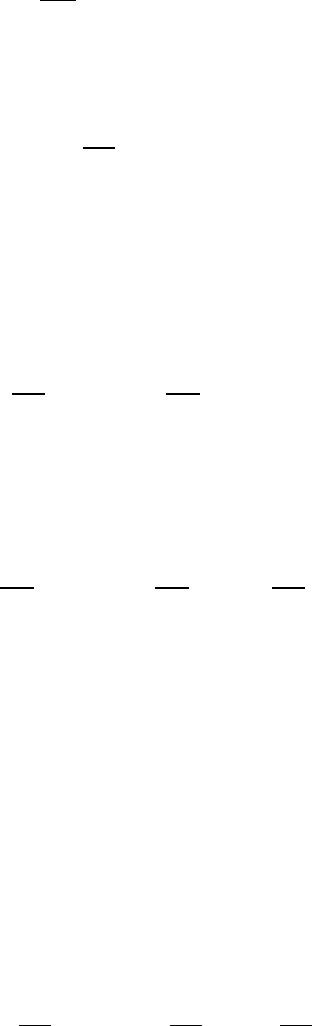
Итак, только при значениях
λ
, равных
λ
n
=
(
πn
ℓ
)
,
(20)
существуют нетривиальные решения задачи (11)
X
n
( x )=sin
πn
ℓ
x,
(21)
определяемые с точностью до произвольного множителя, который мы
положили равным единице. Этим же значениям
λ
n
соответствуют решения
уравнения (9)
T
n
(t )=A
n
cos
πn
ℓ
at+B
n
sin
πn
ℓ
at ,
(22)
где A
n
и B
n
– произвольные постоянные.
Возвращаясь к задаче (1), (9), (10), заключаем, что функции
u
n
( x , t )=X
n
( x )T
n
(t )=
(
A
n
cos
πn
ℓ
at+B
n
sin
πn
ℓ
at
)
sin
πn
ℓ
x
(23)
являются частными решениями уравнения (1), удовлетворяющими граничным
условиям (11) и представимыми в виде произведения (12) двух функций, одна
из которых зависит только от х, другая – от t. Эти решения могут
удовлетворить начальным условиям (10) нашей исходной задачи только для
частных случаев начальных функций (x) и (x).
Обратимся к решению задачи (1), (9), (10) в общем случае. В силу
линейности и однородности уравнения (1) сумма частных решений
u( x ,t )=
∑
n=1
∞
u
n
( x , t )=
∑
n=1
∞
(
A
n
cos
πn
ℓ
at +B
n
sin
πn
ℓ
at
)
sin
πn
ℓ
x
(24)
также удовлетворяет этому уравнению и граничным условиям (9). Начальные
условия позволяют определить A
n
и B
n
. Потребуем, чтобы функция (24)
удовлетворяла условиям (10)

u( x , 0 )=ϕ( x )=
∑
n=1
∞
u
n
(x , 0)=
∑
n=1
∞
A
n
sin
πn
ℓ
x ,
¿
}
¿¿¿
(25)
Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и
кусочно-дифференцируемая функция f(x), заданная в промежутке
0≤x≤ℓ
,
разлагается в ряд Фурье
f (x )=
∑
n=1
∞
b
n
sin
πn
ℓ
x ,
(26)
где
b
n
=
2
ℓ
∫
0
ℓ
f
(
ξ
)
sin
πn
ℓ
ξdξ .
(27)
Если функции (x) и (x) удовлетворяют условиям разложения в ряд
Фурье, то
ϕ( x )=
∑
n=1
∞
ϕ
n
sin
πn
ℓ
x , ϕ
n
=
2
ℓ
∫
0
ℓ
ϕ
(
ξ
)
sin
πn
ℓ
ξdξ ,
(28)
ψ
(
x
)
=
∑
n=1
∞
ψ
n
sin
πn
ℓ
x , ψ
n
=
2
ℓ
∫
0
ℓ
ψ
(
ξ
)
sin
πn
ℓ
ξdξ .
(29)
Сравнение этих рядов с формулами (25) показывает, что для выполнения
начальных условий надо положить
A
n
=ϕ
n
, B
n
=
ℓ
π na
ψ
n
,
(30)
чем полностью определяется функция (24), дающая решение исследуемой
задачи.
Итак, мы доказали, что ряд (24), где коэффициенты A
n
и B
n
определены по
формуле (30), если он допускает двукратное почленное дифференцирование,
представляет функцию u (x, t), которая является решением уравнения (1) и
удовлетворяет граничным и начальным условиям (9) и (10).
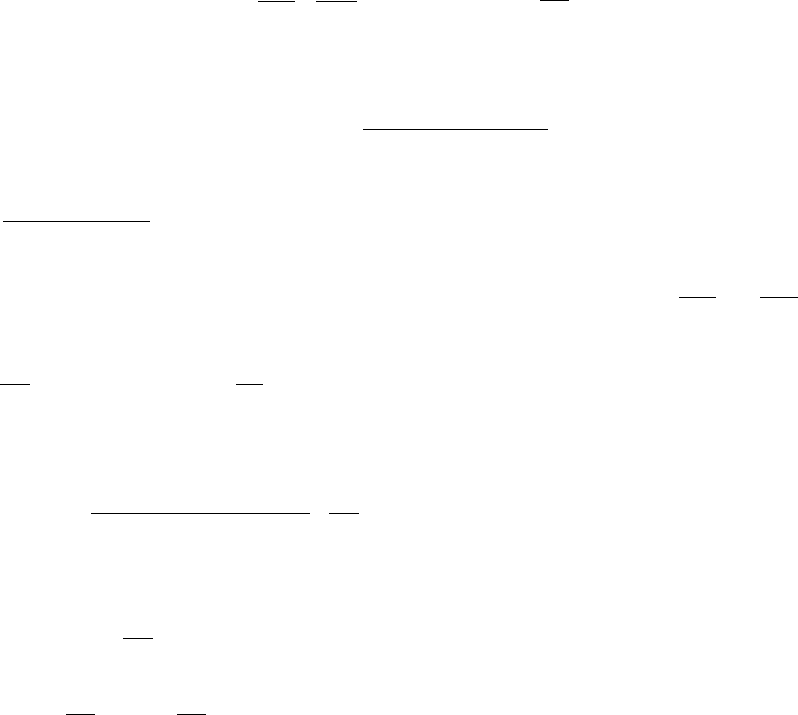
Замечание. Решая рассмотренную задачу для волнового уравнения другим
методом, можно доказать, что ряд (24) представляет решение и в том случае,
когда он не допускает почленного дифференцирования. При этом функция
ϕ
(
x
)
должна быть дважды дифференцируемой, а
ψ
(
x
)
- один раз
дифференцируемой.
Решение уравнений
1. Найти решение уравнения:
∂
2
u
∂ t
2
=
−∂
2
∂ x
2
, если
u ¿
t =0
=x
2
,
∂u
∂ t
¿
t =0
=0
.
Решение:
Так как
a=1
, а
φ
(
x
)
=0
, то
u=
ϕ
(
x−at
)
+ϕ (x +at )
2
, где
ϕ
(
x
)
=x
2
. Таким образом,
u=
(x−t)
2
+(x +t )
2
2
, или
u=x
2
+t
2
.
2. Найти форму струны, определяемой уравнением
∂
2
u
∂ t
2
=a
2
∂
2
u
∂ x
2
в момент
t=
π
2a
, если
u ¿
t =0
=sin x
,
du
dt
¿
t=0
=1
.
Решение:
Имеем
u=
sin (x+at )+sin(x−at)
2
+
1
2 a
∫
x−at
x+at
dz
,
т.е.
u=sin xcos at+
1
2a
z
|
x+at
x−at
, или
u=sin x cos at+t
.
Если
t=
π
2a
, то
u=
π
2a
, т.е. струна параллельна оси абсцисс.

h
0 l x
u
3. Струна, закрепленная на концах
x=0
и
x=t
, имеет в начальный момент
форму параболы
u=
(
4 h
l
2
)
∙ x
(
l−x
)
. Определить
смещение точек струны от оси абсцисс, если
начальные скорости отсутствуют.
Решение:
Здесь
ϕ
(
x
)
=
(
4h
l
2
)
∙ x
(
l−x
)
,
ψ
(
x
)
=0
. Находим коэффициенты ряда, определяющего
решение уравнения колебания струны:
a
k
=
2
l
∫
0
l
φ
(
x
)
∙ sin
kπx
l
dx=
8h
l
3
∫
0
l
(lx−x
2
)∙ sin
kπx
l
dx
;
b
k
=0
.
Для нахождения коэффициента
a
k
дважды интегрируем по частям:
u
1
=lx−x
2
,
d v
1
=sin
kπx
l
dx
,
d u
1
=(l−2 x)dx
,
v
1
=
−l
kπ
cos
kπx
l
;
a
k
=
−8h
l
3
(lx−x
2
)
l
kπ
cos
kπx
l
|
l
0
+
8h
kπ l
2
∫
0
l
(1−2 x )cos
kπx
l
dx
,
т.е.
a
k
=
8h
kπ l
2
∫
0
l
(
1−2 x
)
cos
kπx
l
dx ;
u
2
=l−2x
,
d v
2
=cos
kπx
l
dx
,
d u
2
=−2dx
,
v
2
=
l
kπ
sin
kπx
l
;
a
k
=
8h
k
2
π
2
l
(
1−2 x
)
sin
kπx
l
|
l
0
+
16h
k
2
π
2
l
∫
0
l
sin
kπx
l
dx
=
¿−
16h
k
3
π
3
cos
kπx
l
|
l
0
=
−16 h
k
3
π
3
(
coskπ −1
)
=
16 h
k
3
π
3
[
1−
(
−1
)
k
]
.
Подставляя выражения для
a
k
и
b
k
получим:
u
(
x, t
)
=
∑
n=1
∞
16h
k
3
π
3
[
1−(−1)
k
]
cos
kπat
l
sin
kπx
l
.
Если
k =2 n
, то
1−(−1)
k
=0
, а если
k =2 n+1
, то
1−(−1)
k
=2
; поэтому окончательно
имеем
u
(
x, t
)
=
32h
π
3
∑
n=1
∞
1
(2 n+1)
3
cos
(2 n+1)πat
l
sin
(2 n+1)πx
l

Пусть начальные отклонения струны, закрепленной в точках
x=0
и
x=l
, равны
нулю, а начальная скорость выражается формулой
∂u
∂ t
=
{
v
0
(
const
)
при
|
x−l/2
|
<h/2,
0 при
|
x−l/2
|
>h/2 .
Определить форму струны для любого момента времени t.
Решение:
Здесь
φ
(
x
)
=0
, а
ψ
(
x
)
=v
0
в интервале
(
l−h
)
/2
,
(
l+h
)
/2
и
ψ
(
x
)
=0
вне этого интервала.
Следовательно,
a
k
=0
;
b
k
=
2
kπa
∫
(l−h)/2
(l +h)/2
v
0
sin
kπx
l
dx=
−2v
0
kπa
∙
l
kπ
∙cos
kπx
l
¿¿
¿
2v
0
l
k
2
π
2
a
[
cos
kπ (l−h)
2l
−cos
kπ (1+h)
2l
]
=
4 v
0
l
k
2
π
2
a
∙sin
kπ
2
∙sin
kπh
2l
.
Отсюда
u
(
x, t
)
=
4 v
0
l
π
2
a
∑
k=1
∞
1
k
2
∙sin
kπ
2
∙sin
kπh
2l
∙ sin
kπat
l
∙sin
kπx
l
,
Или
u
(
x, t
)
=
4 v
0
l
π
2
a
(
sin
πh
2l
∙sin
πat
l
∙ sin
πx
l
−
1
3
2
∙sin
3πh
2l
×
×sin
3πat
l
sin
3 πx
l
+
1
5
2
∙ sin
5 πh
2l
∙ sin
5 πat
l
∙ sin
5πx
l
−…
)

Глава 2. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
§2.1 Уравнение распространения тепла в стержне.
Рассмотрим однородный стержень длины
ℓ
. Будем предполагать, что
боковая поверхность стержня теплонепроницаема и что во всех точках
поперечного сечения стержня температура одинакова. Изучим процесс
распространения тепла в стержне.
Расположим ось Ох так, что один конец стержня будет совпадать с точкой
х = 0, а другой – с точкой х =
ℓ
.
Рис. 2.1.
Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t.
Опытным путем установлено, что скорость распространения тепла, т. е.
количество тепла, протекающего через сечение с абсциссой х за единицу
времени, определяется формулой
q=−k
∂u
∂ x
S ,
(1)
где S – площадь сечения рассматриваемого стержня, k – коэффициент
теплопроводности.
Рассмотрим элемент стержня, заключенный между сечениями с
абсциссами х
1
и х
2
(х
2
– х
1
=
Δ
х). Количество тепла, прошедшего через
сечение с абсциссой х
1
за время
Δ
t, будет равно
ΔQ
1
=−k
∂ u
∂ x
|
x =x
1
SΔt,
(2)
то же самое с абсциссой х
2
:
ΔQ
2
=−k
∂ u
∂ x
|
x=x
2
SΔt .
(3)
0
x
1
x
2
ℓ
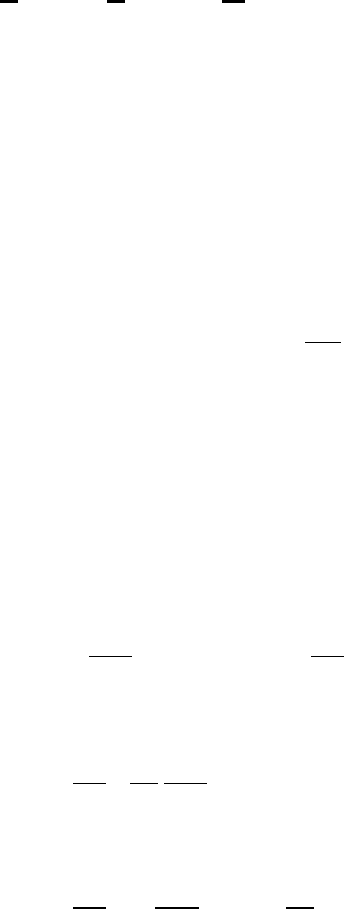
Приток
Δ
Q
1
-
Δ
Q
2
в элемент стержня за время
Δ
t будет равняться:
ΔQ
1
− ΔQ
2
=
[
−k
∂ u
∂ x
|
x=x
1
SΔt
]
−
[
−k
∂u
∂ x
|
x= x
2
SΔt
]
≈¿ ¿¿k
∂
2
u
∂ x
2
Δ xS Δt
(4)
Этот приток тепла за время
Δ
t затратился на повышение температуры
элемента стержня на величину
Δ
u:
ΔQ
1
− ΔQ
2
=cρΔ xS Δu
или
ΔQ
1
− ΔQ
2
≈cρΔ xS
∂ u
∂ x
Δt ,
(5)
где с – теплоемкость вещества стержня,
ρ
– плотность вещества стержня (
ρ
Δ
xS – масса элемента стержня).
Приравнивая выражения (4) и (5) одного и того же количества тепла
ΔQ
1
− ΔQ
2
, получим:
k
∂
2
u
∂ x
2
Δ xS Δt=cρΔ xS
∂u
∂t
Δt
или
∂u
∂t
=
k
cρ
∂
2
u
∂ x
2
или
∂u
∂t
=a
2
∂
2
u
∂ x
2
, где
k
cρ
=a
2
.
Это и есть уравнение распространения тепла (уравнение
теплопроводности) в однородном стержне.
Чтобы решение уравнения (6) было вполне определено, функция u (x, t)
должна удовлетворять краевым условиям, соответствующим физическим
условиям задачи. Краевые условия для решения уравнения (6) могут быть
(6)

различные. Условия, которые соответствуют так называемой первой краевой
задаче для
0≤t≤T
, следующие:
u (x, 0) = φ(x), (7)
u (0, t) = ψ
1
(t), (8)
u (
ℓ
, t) = ψ
2
(t). (9)
Физическое условие (7) (начальное условие) соответствует тому, что при
t=0
в разных сечениях стержня задана температура, равная φ(x). Условия (8)
и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0
и при х =
ℓ
поддерживается температура, равная ψ
1
(t) и ψ
2
(t) соответственно.
Доказывается, что уравнение (6) имеет единственное решение в области
0<x <ℓ , 0<t<T
, удовлетворяющее условиям (7) – (9).
Решение задач:
1. Задача:
Решить уравнение
x
∂u
∂ x
+ y
∂u
∂ y
+( z +u )x
∂ u
∂ z
=xy
.
Решение. Составим и решим систему уравнений характеристик
dx
x
=
dy
y
=
dz
z+u
=
du
xy
Уравнение
dx
x
=
dy
y
даёт первый интеграл
C
1
=
y
x
. Преобразуем три дроби
dx
x
=
dy
x
=
du
xy
, используя правило работы с равными дробями:
ydx +xdy
yx +xy
=
du
xy
⇒
d (xy )
2 xy
=
du
xy
⇒ d (xy )=2 du
.
Отсюда получим второй первый интеграл
C
2
=
(
1
2
)
xy −u
.
