Курсовая работа - Численное решение дифференциального уравнения в частных производных параболического типа

Подождите немного. Документ загружается.

Министерство образования РФ

Тульский государственный университет

Кафедра РТиРТС

Курсовая работа по програмированнию и основам олгаритмизации:

Численное решение дифференциального уравнения

в частных производных параболического типа

Выполнил: студент гр. 120671 Долгов А.А

Проверил: ________________

Тула 2008г

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

Оглавление

Теоретическое описание.........................................................................................3

Постановка задачи...................................................................................................8

Блок-схема алгоритма.............................................................................................9

Программа расчета................................................................................................10

Тесты программы..................................................................................................13

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

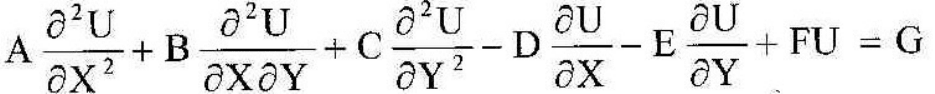
Теоретическое описание

Большинство процессов, встречающихся в практике

инженера, занимающегося проектированием и совершенствованием

двигателя, это процессы, в которых взаимосвязаны множество различных

параметров, зависящих от нескольких независимых переменных. Такие

процессы чаще всего описываются дифференциальными уравнениями в

частных производных с заданными краевыми условиями. Примерами могут

служить уравнения газовой динамики, нестационарной теплопроводности,

механики деформируемого тела и другие. Независимыми переменными в

таких задачах являются время и пространственные координаты.

Дифференциальные уравнения в частных производных составляют в

настоящее время одну из наиболее развивающихся отраслей численного

анализа. Возможности современных ЭВМ позволяют ставить на повестку дня

такие задачи, решение которых просто немыслимо без использования

вычислительных машин.

Рассмотрим общий подход к решению таких уравнений и

проанализируем некоторые численные методы и соответствующие им

программы расчета, которые часто используются в инженерной практике и

могут оказаться полезными во многих случаях.

При переходе от одной к нескольким переменным разнообразие и

сложность задач резко возрастает. Наше рассмотрение будет ограничено

линейными дифференциальными уравнениями второго порядка с двумя

независимыми переменными. Эти уравнения в общем виде можно записать:

где А, В, С, D, Е, F, G являются функциями только от независимых

переменных Х и У.

Как и в случае обыкновенного дифференциального уравнения, для

отыскания единственного решения, отвечающего реальному процессу,

необходимо добавить краевые (граничные, начальные) условия.

Дифференциальные уравнения в частных производных второго порядка

разделяются на три типа:

1) Уравнение эллиптического типа, если в

- 4АС < 0

2) Уравнение параболического типа, если в

- 4АС = 0

3) Уравнение гиперболического типа, если в

- 4АС > 0

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

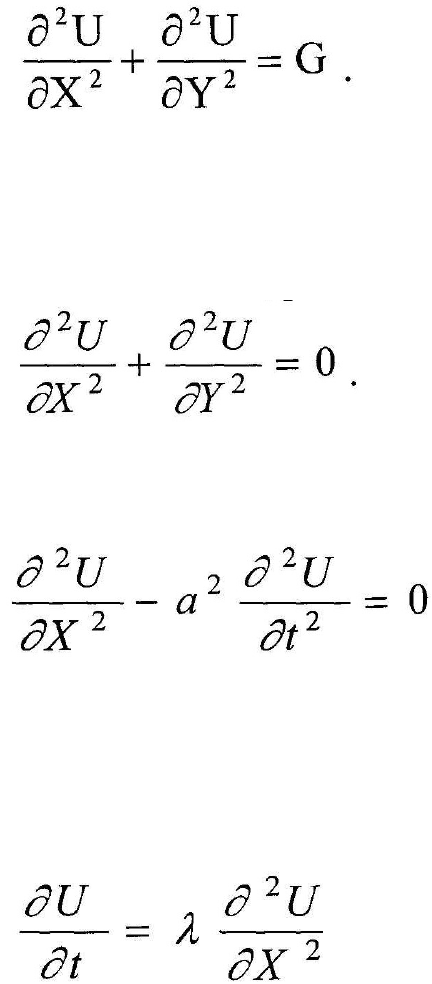
Уравнения различаются в связи с существенным отличием характера их

решения для каждого из указанных типов. Уравнения эллиптического типа

встречаются в расчетах напряжений при упругом кручении длинного

цилиндрического стержня, дозвукового течения газового потока,

стационарного температурного поля в элементах конструкций, например:

Это уравнение носит название уравнения Пуассона. Его часто

записывают в виде Δ U = G или V

U = G.

Частным случаем этого уравнения является уравнение Лапласа

Характерным примером гиперболического уравнения является

уравнение колебания упругой нити, называемое волновым уравнением:

к гиперболическим уравнениям приводятся также задачи сверхзвукового

течения газа, динамические задачи упругости и теплопроводности.

Параболическими уравнениями описываются процессы не стационарно

теплопроводности в двигателе, диффузии:

Для построения численного метода решения рассматриваемых задач

заменяют область непрерывного изменения аргументов Х , У расчетной

сеткой дискретным множеством точек с координатами X

, Y

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

J=4

J=3

J=2

U(3,2)

J=1

i=1 I=2 i=3 i=4

В рассмотрение вводятся два параметра: ΔХ, ΔУ - шаги сетки по

координатам Х и У соответственно. Вместо функции U( Х, У )

рассматривают сеточную функцию, соответствующую точкам сетки X

, Y

•

Далее заменяют частные производные, входящие в дифференциальные

уравнения, разностными соотношениями, полученными ранее при

рассмотрении обыкновенных дифференциальных уравнений:

В результате замены частных производных в дифференциальных

уравнениях разностными выражениями получают разностное уравнение.

Разумеется, способов замены дифференциального уравнения разностными -

множество. Получаемые разностные уравнения будут отличаться точностью,

скоростью сходимости, устойчивостью и другими свойствами. Указанные

вопросы исследуются в теории численных методов.

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

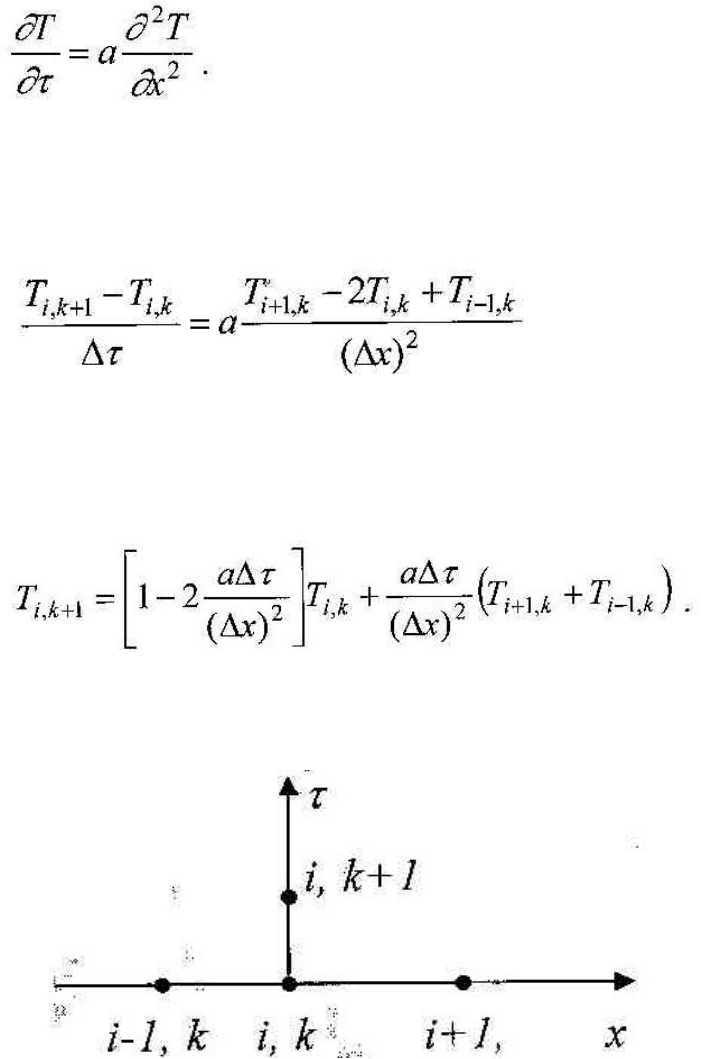
Рассмотрим некоторые особенности численного решения

дифференциального уравнения параболического типа на примере

одномерного уравнения теплопроводности

В простейшем варианте конечно-разностное уравнение,

соответствующее данному дифференциальному уравнению, можно

представить в виде

в данном случае неизвестным является значение Ti,k+ 1 , И оно явно

выражается через известные узловые значения температуры на предыдущем

временном слое "k":

в соответствии с этим такая схема носит название явной разностной

схемы.

Явная разностная схема имеет первый порядок точности по времени и

второй порядок - по пространственной координате. Ее погрешность

оценивается величиной О( Δτ + Δх

)

Явная схема обладает условной устойчивостью, условие устойчивости

имеет вид

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

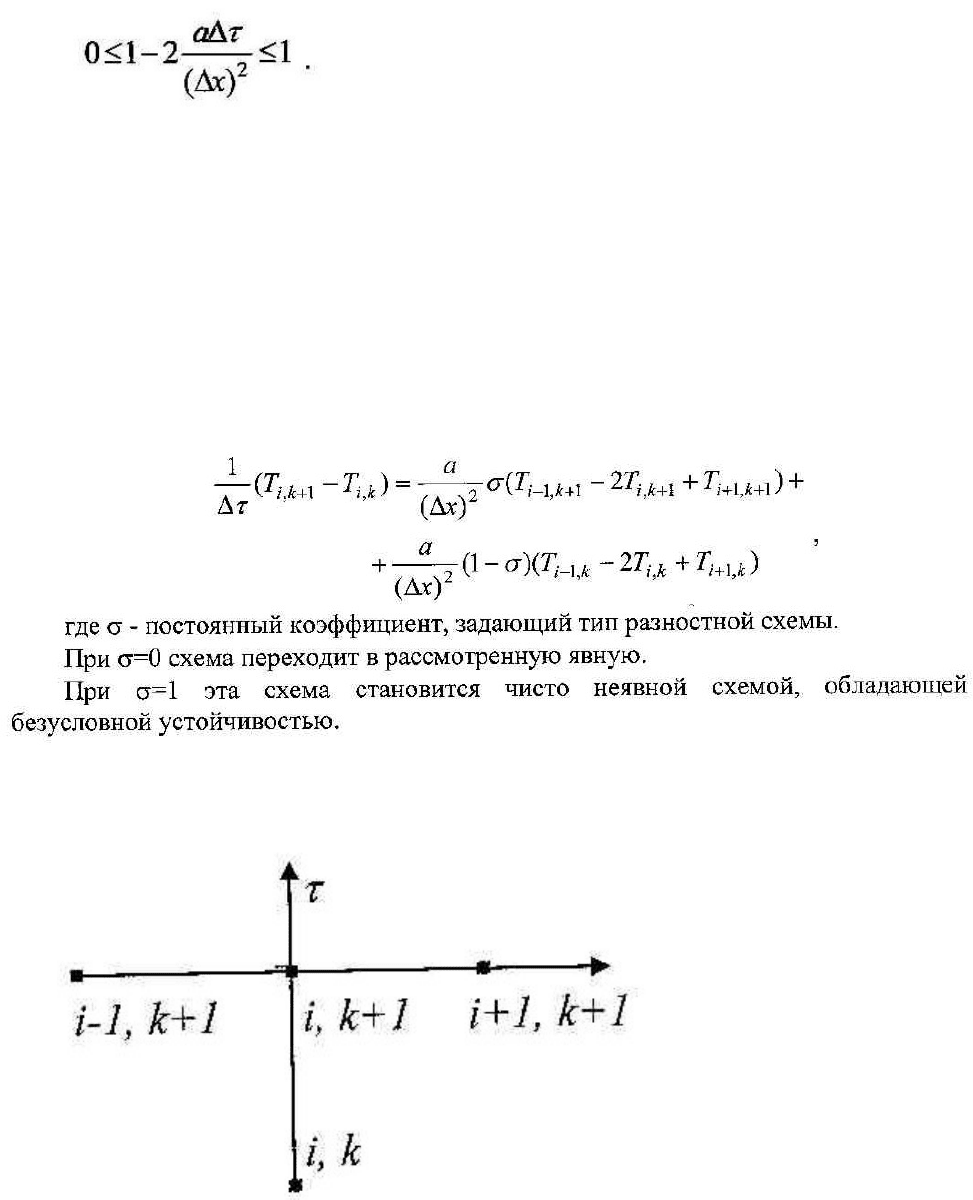
Данное условие приводит к необходимости задавать в практических

расчетах очень маленькие величины шагов интегрирования по времени

(существенно меньше, чем того требует условие точности решения) , а это

приводит к увеличению времени решения задачи на ЭВМ и нарастанию

погрешности округления чисел.

В связи с отмеченным широкое распространение получили неявные

схемы расчета, позволяющие смягчить условие устойчивости. Семейство

двухслойных неявных схем для уравнения теплопроводности запишем в виде

Следует отметить, что расчет по неявной схеме требует на каждом шаге

интегрирования по времени решения системы алгебраических уравнений,

связывающих неизвестные температуры узловых точек временного слоя

К + 1.

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

Постановка задачи

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

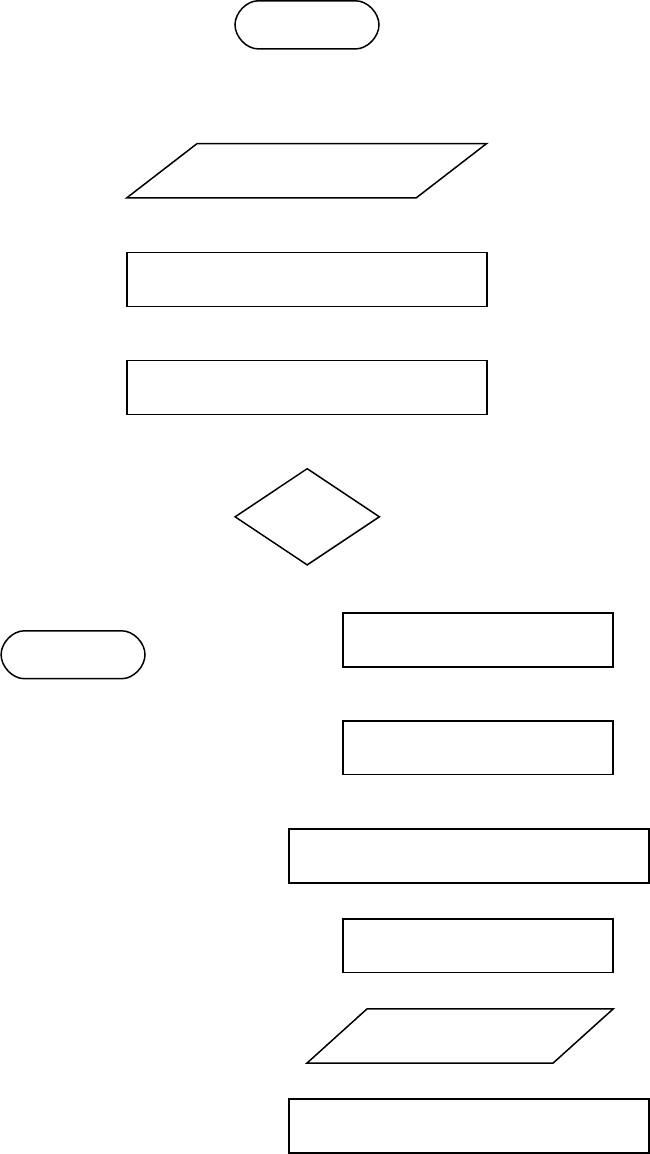
Блок-схема алгоритма

нет да

начало

конец

i<r

Ввод:

r,a,b,c,x,dx,T

p1:=1-2*a*dt/(b*c*dx*dx);)

p2:=a*dt/(b*c*dx*dx);)

T(x,t+1)=p1*T[1]+p2*(T[2]+T[0]

)

T[1]=T(Xi,t)

T[2]=T(X

i+1

,t)

T[0]=T(X

i-1

,t)

Вывод

T(x,t+1)

i=i+1

Программа расчета

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs, StdCtrls, ExtCtrls, Menus;

type

TForm1 = class(TForm)

RadioGroup1: TRadioGroup;

Edit1: TEdit;

Edit2: TEdit;

Label1: TLabel;

Label2: TLabel;

Button1: TButton;

ListBox1: TListBox;

PopupMenu1: TPopupMenu;

dx1: TMenuItem;

Label3: TLabel;

Label4: TLabel;

Label5: TLabel;

N1: TMenuItem;

procedure setparam;

procedure Button1Click(Sender: TObject);

procedure RadioGroup1Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure dx1Click(Sender: TObject);

procedure N1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

T:array[0..3] of currency;

r, a,b,c:integer;

dx,dt,X,p1,p2:currency;

s:string;

implementation

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

var i:integer;

begin