Курсовая работа - Б-деревья во внешней памяти
Подождите немного. Документ загружается.


2 y: BTreeNode;
3 begin
4 i := x.n;
5 if x.leaf then
6 begin
7 while (i >= 1) and (k < x.key[i]) do
8 begin
9 x.key[i + 1] := x.key[i];
10 i := i - 1;
11 end;
12 x.key[i + 1] := k;
13 x.n := x.n + 1;
14 DiskWrite(x);
15 end
16 else
17 begin
18 while (i >= 1) and (k < x.key[i]) do
19 i := i - 1;
20 i := i + 1;
21 y := DiskRead(x.c[i]);
22 if y.n = 2 * t - 1 then
23 begin
24 SplitChild(x, y, i);
25 if k > x.key[i] then
26 begin
27 i := i + 1;
28 y := DiskRead(x.c[i]);
29 end;
30 end;
31 InsertNonFull(y, k);
32 end;
33 end;
Процедура TBTree.InsertNonFull работает следующим образом. Строки 5-15
обрабатывают случай, когда х является листом; при этом ключ k просто
вставляется в данный лист. Если же x не является листом, то мы должны вставить
k в подходящий лист в поддереве, корнем которого является внутренний узел х. В
этом случае строки 18-19 определяют дочерний узел x, в который спустится
рекурсия. В строке 22 проверяется, не заполнен ли этот дочерний узел, и если он
заполнен, то вызывается процедура TBTree.SplitChild, которая разбивает его на
два незаполненных узла, а строки 25-29 определяют, в какой из двух
получившихся в результате разбиения узлов должна спуститься рекурсия.
Сложность алгоритма
Количество обращений к диску, выполняемых процедурой TBTree.Insert для
В-дерева высотой h, составляет О(h), поскольку между вызовами
TBTree.InsertNonFull выполняется только O(1) операций DiskWrite и DiskRead.
14
Необходимое процессорное время равно O(th) = O(t log
t
n). Поскольку в
TBTree.InsertNonFull использована оконечная рекурсия, ее можно реализовать
итеративно с помощью цикла while, наглядно показывающего, что количество
страниц, которые должны находиться в оперативной памяти, в любой момент
времени равно O(1).
3.1.2. Операция удаления ключа.
Удаление ключа из В-дерева, хотя и аналогично вставке, представляет собой
более сложную задачу. Это связано с тем, что ключ может быть удален из любого
узла, а не только из листа, а удаление из внутреннего узла требует определенной
перестройки дочерних узлов. Как и в случае вставки, мы должны обеспечить,
чтобы при выполнении операции удаления не были нарушены свойства В-дерева.
Аналогично тому, как мы имели возможность убедиться, что узлы не
слишком сильно заполнены для вставки нового ключа, нам предстоит убедиться,
что узел не становится слишком мало заполнен в процессе удаления ключа (за
исключением корневого узла, который может иметь менее t-1 ключей, хотя и не
может иметь более 2t-1 ключей).
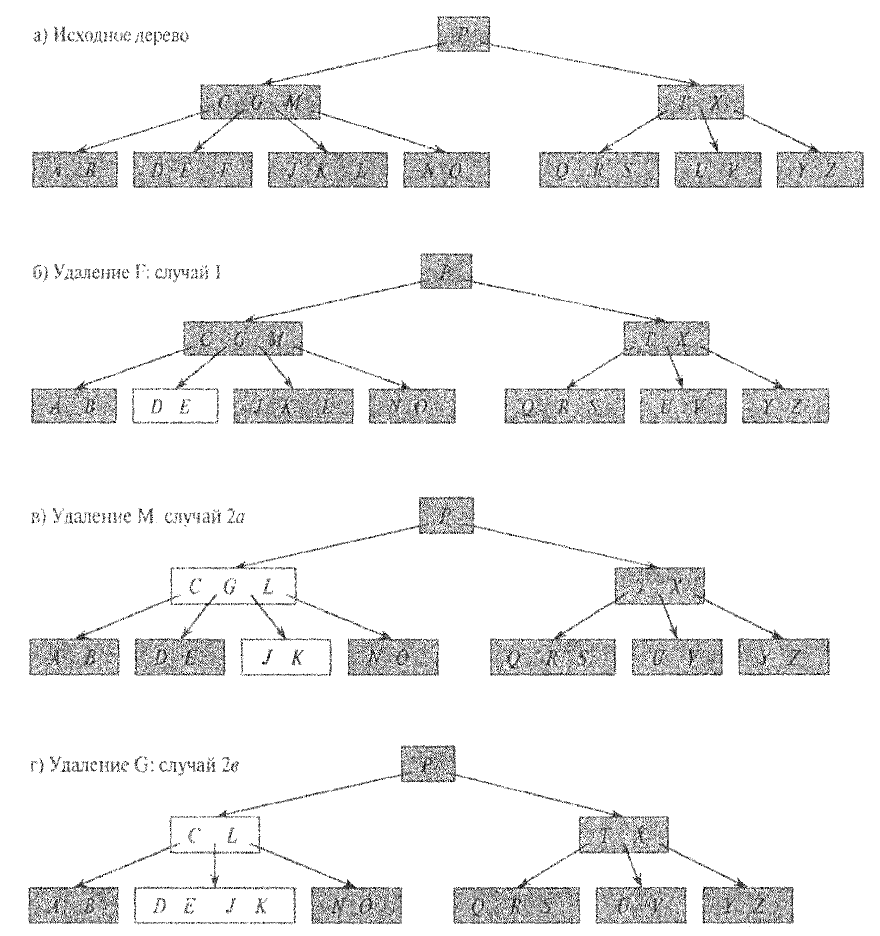
При удалении ключа могут возникнуть следующие случаи:
1. Если ключ k находится в узле x и x является листом — удаляем k из x.
2. Если ключ k находится в узле x и x является внутренним узлом, выполняем
следующие действия:
1) Если дочерний по отношению к x узел y, предшествующий ключу k в
узле x, содержит не менее t ключей, то находим k` — предшественника k
в поддереве, корнем которого является y. Рекурсивно удаляем k` и
заменяем k в x ключом k`. (Поиск ключа k` и удаление его можно
выполнить в процессе одного нисходящего прохода.)
2) Ситуация, симметричная ситуации а) если дочерний по отношению к x
узел z, следующий за ключом k в узле x, содержит не менее t ключей, то
15
находим k` — следующий за k ключ в поддереве, корнем которого
является z. Рекурсивно удаляем k` и заменяем k в x ключом k`. (Поиск
ключа k` и удаление его можно выполнить в процессе одного
нисходящего прохода.)
3) В противном случае, если и y, и z содержат по t-1 ключей, вносим k и все
ключи z в y (при этом из x удаляется к и указатель на z, а узел y после
этого содержит 2t — 1 ключей), а затем освобождаем z и рекурсивно
удаляем k из y.
3. Если ключ k отсутствует во внутреннем узле x, находим корень x.c[i]
поддерева, которое должно содержать k (если таковой ключ имеется в
данном В-дереве). Если x.c[i] содержит только t-1 ключей, выполняем шаг
За или 3б для того, чтобы гарантировать, что далее мы переходим в узел,
содержащий как минимум t ключей. Затем мы рекурсивно удаляем k из
поддерева с корнем x.c[i],
1) Если x.c[i] содержит только t-1 ключей, но при этом один из ее
непосредственных соседей (под которым мы понимаем дочерний по
отношению к x узел, отделенный от рассматриваемого ровно одним
ключом-разделителем) содержит как минимум t ключей, передадим в
x.c[i] ключ-разделитель между данным узлом и его непосредственным
соседом из x, на его место поместим крайний ключ из соседнего узла и
перенесем соответствующий указатель из соседнего узла в x.c[i].
2) Если и x.c[i] и оба его непосредственных соседа содержат по t-1 ключей,
объединим x.c[i] с одним из его соседей (при этом бывший ключ-
разделитель из х станет медианой нового узла).
В случае 3 при рассмотрении соседей мы должны учесть, что у рассматриваемого
узла может быть только один сосед (правый или левый).
16
17
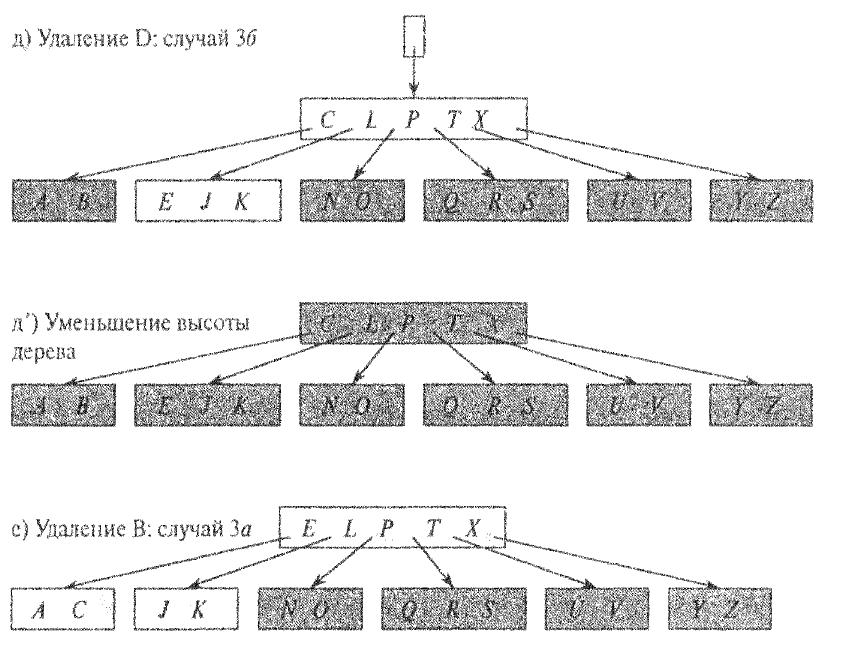
Рис. 4. Удаление узла из дерева с минимальной степенью 3.
Полный код функции удаления и остальных функций представлены в
Приложении А.
3.2. Реализация интерфейса.
При изменении дерева было решено не выводить старый и новый вариант
дерева в соответствующие компоненты TTreeView. Вместо этого компоненты
меняются местами, и происходит вывод только в компонент TTreeView, который
содержит модифицированное дерево. Для запоминания компонента с
обновленной версией дерева используется глобальная переменная TreeView.
18
Заключение.
В ходе курсовой работы были выполнены следующие задачи:
изучены приемы работы с B-деревьями;
создан класс B-дерева;
разработана программа, демонстрирующая работу класса.
Программа демонстрирует технику внутренней реализации операций
добавления, удаления, поиска элемента в B-дереве, которое хранится во внешней
памяти.
19
Список использованных источников.
1. Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд
Штайн «Алгоритмы: построение и анализ». — 2-е изд. — М.: «Вильямс», 2006
2. Кнут Д. Э. «Искусство программирования», т.3. "Вильямс", Москва-
Петербург-Киев, 2000 г.
3. Альфред В. Ахо, Джеффри Д. Ульман, Джон Э. Хопкрофт, «Структуры
данных и алгоритмы», издательство "Вильямс", 2000 г
20

Приложение А. Модуль класса «B-дерево».
1 unit BTree;
2
3 interface
4 uses Classes, SysUtils, Dialogs;
5
6 const t = 4; //порядок дерева
7
8 type
9 BTreeNode = record
10 n: integer; //количество ключей, хранящихся в настоящий момент в узле х.
11 pos: integer; //позиция текущего узла в файле
12 key: array[1..2 * t - 1] of integer;
13 c: array[1..2 * t] of integer;
14 leaf: boolean; //TRUE, если х является листом, и false, если х — внутренний узел.
15 end;
16
17 TBTree = class(TObject)
18 private
19 RemMas: array of integer; //массив удаленных записей
20 RemMasChange: boolean;
21 procedure AddToRemMas(var r: integer);
22 function GetFreePos(DefaultPos: integer): integer;
23 function GetCount(): integer;
24 function AllocateNode(): BTreeNode;
25 procedure SplitChild(var x, y: BTreeNode; i: integer);
26 procedure InsertNonFull(var x: BTreeNode; k: integer);
27 function MaxInSubTree(var pos: integer): integer;
28 function MinInSubTree(var pos: integer): integer;
29 public
30 RootPos: integer;
31 RemCount: integer; // размер RemMas в файле
32 FileName: string;
33 constructor Create(BTreeFileName: string);
34 property Count: integer read GetCount;
35 function DiskRead(var pos: integer): BTreeNode;
36 procedure DiskWrite(var x: BTreeNode);
37 procedure Open(SrcFileName: string);
38 procedure SaveAs(DstFileName: string);
39 function Search(var pos, k: Integer): boolean;
40 procedure Insert(var k: integer); // встака влюча
41 function Remove(var x_num: integer; k: integer): boolean;
42 procedure UpdateFile();
43 end;
44
45
46 implementation
47
48 function TBTree.GetCount: integer;
49 var s: TStream;
50 begin
51 Result := 0;
52 try
53 s := TFileStream.Create(FileName, fmOpenRead);
54 Result := (s.Size - (RemCount + 2) * SizeOf(integer)) div
sizeOf(BTreeNode);
55 s.Free();
21

56 except
57 ShowMessage('Ошибка при чтении файла');
58 end;
59 end;
60
61 procedure TBTree.AddToRemMas(var r: integer);
62 begin
63 SetLength(RemMas, Length(RemMas) + 1);
64 RemMas[Length(RemMas) - 1] := r;
65 RemMasChange := true;
66 end;
67
68 function TBTree.AllocateNode(): BTreeNode;
69 var x: BTreeNode;
70 i: integer;
71 begin
72 x.pos := 0;
73 x.n := 0;
74 x.leaf := false;
75 for i := 1 to 2 * t - 1 do
76 begin
77 x.key[i] := -1;
78 x.c[i] := -1;
79 end;
80 x.c[2 * t] := -1;
81 Result := x;
82 end;
83
84 function TBTree.DiskRead(var pos: integer): BTreeNode;
85 var x: BTreeNode;
86 s: TStream;
87 begin
88 try
89 s := TFileStream.Create(FileName, fmOpenRead);
90 s.Seek(pos * SizeOf(x) + (RemCount + 2) * SizeOf(integer),
soFromBeginning);
91 s.ReadBuffer(x, SizeOf(x));
92 s.Free();
93 Result := x;
94 except
95 ShowMessage('Ошибка при чтении файла');
96 end;
97 end;
98
99 function TBTree.GetFreePos(DefaultPos: integer): integer;
100 begin
101 if Length(RemMas) = 0 then
102 Result := DefaultPos
103 else
104 begin
105 Result := RemMas[Length(RemMas) - 1];
106 SetLength(RemMas, Length(RemMas) - 1);
107 end;
108 end;
109
110
111 procedure TBTree.DiskWrite(var x: BTreeNode);
112 var //x: BTreeNode;
113 s: TStream;
114 begin
115 try
116 s := TFileStream.Create(FileName, fmOpenWrite);
117 s.Seek(x.pos * SizeOf(x) + (RemCount + 2) * SizeOf(integer),
soFromBeginning);
22

118 s.WriteBuffer(x, SizeOf(x));
119 s.Free();
120 except
121 ShowMessage('Ошибка при открытии или записи в файл');
122 end;
123 end;
124
125
126 constructor TBTree.Create(BTreeFileName: string);
127 var s: TStream;
128 root: BTreeNode;
129 begin
130 root := AllocateNode();
131 root.n := 0;
132 root.leaf := true;
133 root.pos := 0;
134
135 RootPos := root.pos;
136 RemCount := 0;
137 SetLength(RemMas, 0);
138
139 FileName := BTreeFileName;
140 s := TFileStream.Create(FileName, fmCreate);
141 s.Seek(0, soFromBeginning);
142 s.WriteBuffer(RootPos, SizeOf(integer));
143 s.WriteBuffer(RemCount, SizeOf(integer));
144 s.WriteBuffer(root, SizeOf(root));
145 s.Free();
146
147 RemMasChange := false;
148 end;
149
150 procedure TBTree.Open(SrcFileName: string);
151 var
152 s: TStream;
153 i: integer;
154 begin
155 FileName := SrcFileName;
156 try
157 s := TFileStream.Create(FileName, fmOpenRead);
158 s.Seek(0, soFromBeginning);
159 s.ReadBuffer(RootPos, SizeOf(RootPos));
160 s.ReadBuffer(RemCount, SizeOf(RemCount));
161
162 SetLength(RemMas, 0);
163 for i := 0 to RemCount - 1 do
164 begin
165 SetLength(RemMas, Length(RemMas) + 1);
166 s.ReadBuffer(RemMas[Length(RemMas) - 1], SizeOf(integer));
167 end;
168 s.Free();
169 except ShowMessage('Ошибка при открытии файла');
170 end;
171 end;
172
173 procedure TBTree.SaveAs(DstFileName: string);
174 procedure FileCopy(const FSrc, FDst: string);
175 var
176 sStream,
177 dStream: TFileStream;
178 begin
179 sStream := TFileStream.Create(FSrc, fmOpenRead);
180 try
181 dStream := TFileStream.Create(FDst, fmCreate);
23
