Кумыкова С.К., Нахушева Ф.Б. Математика: Практикум по аналитической геометрии и алгебре

Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КАБАРДИНО-БАЛКАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

МАТЕМАТИКА

ПРАКТИКУМ

ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ И АЛГЕБРЕ

Для специальности: 011000 – Химия

НАЛЬЧИК 2004

УДК 519,2 (075.3)

ББК 22. 17173

Рецензент:

доцент кафедры высшей математики Кабардино-Балкарской

государственной сельскохозяйственной академии

И.Х. Керефова

Составители: Кумыкова С.К., Нахушева Ф.Б.

Математика. Практикум по аналитической геометрии и алгебре.

– Нальчик: Каб.-Балк. ун-т., 2004. – 59 с.

Издание содержит теоретический минимум, методические указания к

решению задач по аналитической геометрии и высшей алгебре, образцы ре-

шения типовых задач и задач по химии.

Предназначено для студентов, магистрантов и аспирантов специально-

сти "Химия".

Рекомендовано РИСом университета

УДК 519,2 (075.3)

ББК 22. 17173

ã Кабардино-Балкарский государственный

университет, 2004

ВВЕДЕНИЕ

Математика играет важную роль в естественнонаучных, инженерно-

технических и гуманитарных исследованиях. Без современной математики с

ее развитым логическим и вычислительным аппаратом был бы невозможен

прогресс в различных областях человеческой деятельности.

Математика является не только мощным средством решения приклад-

ных задач и универсальным языком науки, но также и элементом общей

культуры. Поэтому математическое образование следует рассматривать как

важнейшую составляющую часть в системе фундаментальной подготовки

современного химика.

Курс математики имеет прикладную направленность и содержит мно-

гообразие тем с примерами и задачами из химии, что позволит овладеть ма-

тематическими методами решения химических задач и связать абстрактные

понятия математики с конкретными понятиями химической техники.

Использование приемов высшей математики в решении химических и

химико-технологических вопросов позволяет получить наиболее ценные ре-

зультаты, достижение которых иными путями часто оказывается невозмож-

ным. Для химика важно умение пользоваться математическим аппаратом и

умение выбрать из многочисленных методов и приемов математики те, кото-

рые нужны для решения конкретной инженерной задачи.

Данное методическое пособие написано с целью помочь химикам эф-

фективно использовать высшую математику в практической деятельности.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ ПО МАТЕМАТИКЕ

Аналитическая геометрия на плоскости.

Прямоугольные и полярные координаты

Если на плоскости задана прямоугольная декартова система координат

xOy, то расстояние d между точками M

) и M

) определяется по

формуле

( )( )

yyxxd -+-= . (1)

В частности, расстояние d точки M(x;y) от начала координат определя-

ется по формуле

yxd += . (2)

Координаты точки

(

)

y;xC , делящей отрезок между точками A(x

) и

B(x

) в заданном отношении l, определяются по формулам

;

. (3)

При l=1 получаются формулы для координат середины отрезка:

= ;

. (4)

Площадь треугольника с вершинами A(x

), B(x

), C(x

) опреде-

ляется по формуле

( )( )( )( )

.yyxxyyxx

12131312

-----= (5)

Формулу для площади треугольника можно записать в виде

S = , где

321

yyy

xxx

111

. (6)

В полярной системе координат положение точки M на плоскости оп-

ределяется ее расстоянием |OM|=

от полюса О (

– полярный радиус-

вектор точки) и углом q, образованным отрезком OM с полярной осью Ox

(q – полярный угол точки). Угол q считается положительным при отсчете от

полярной оси против часовой стрелки.

Если начало декартовой прямоугольной системы координат совместить с

полюсом, а ось Ox направить по полярной оси, то прямоугольные координаты x и y

точки M и ее полярные координаты

и q связаны следующими формулами:

sin

cos

; (7)

x/ytg,yx =+=

. (8)

1. Показать, что треугольник с вершинами A(-3;-3), B(-1;3), C(11;-1) –

прямоугольный.

∆ Найдем длины сторон треугольника:

( )( ) ( )( ) ( )( )

.20031311AC,403331AB,16031111BC

222222

=+-++==+++-==--++=

Так как |AB|

=40, |BC|

=160, |AC|

=200, то |AB|

+|BC|

=|AC|

. Таким об-

разом, сумма квадратов длин двух сторон треугольника равна квадрату дли-

ны третьей стороны. Отсюда заключаем, что треугольник ABC прямоуголь-

ный и сторона AC является его гипотенузой. ▲

2. Известны точки A(-2;5), B(4;17) – концы отрезка AB. На этом отрез-

ке находится точка C, расстояние которой от A в два раза больше расстояния

от B. Определить координаты точки C.

∆ Так как |AC|=2|CB|, то l=|AC|:|CB|=2. Здесь x

=-2, y

=5, x

=4, y

=17.

Следовательно,

,13

1725

y,2

422

x =

т.е. C(2;13). ▲

3. Даны вершины треугольника ABC: A(x

), B(x

), C(x

). Опре-

делить координаты точки пересечения медиан треугольника.

∆ Находим координаты точки D – середины отрезка AB; имеем

=(x

)/2, y

=(y

)/2. Точка M, в которой пересекаются медианы, делит

отрезок CD в отношении 2:1, считая от точки C. Следовательно, координаты

точки M определяются по формулам

y2y

x2x

D3D3

= т.е.

(

)

(

)

213213

/yyy

/xxx

= .

Окончательно получаем

yyy

xxx

321321

= . ▲

4. Определить площадь треугольника с вершинами A(-2;-4), B(2;8),

C(10;2).

∆ Используя формулу (5), получаем

( )( )( )( )

6014424

482104222

S =-=++-++= (кв. ед.). ▲

5. Найти полярные координаты точки

(

)

31 -;M , если полюс совпадает с на-

чалом координат, а полярная ось – с положительным направлением оси абсцисс.

∆ На основании равенств (8) находим

(

)

3tg;231

-==-+=

Очевидно, что точка M лежит в IV четверти и, следовательно, q=5p/3. Итак,

M(2;5

/3). ▲

6. Найти прямоугольные координаты точки

(

)

4/3;22A

, если полюс

совпадает с началом координат, а полярная ось направлена по оси абсцисс.

∆ Используя формулы (7), имеем

sin22y,2

cos22x ==-==

. Итак, A(-2;2). ▲

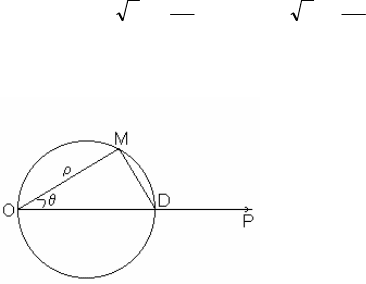
7. Найти уравнение окружности, проходящей через полюс, если центр

окружности лежит на полярной оси, а радиус равен a.

∆ Координатами точки M будут угол

q и длина ∆ отрезка OM. Из прямоугольно-

го треугольника OMD сразу получаем ис-

комое уравнение

∆=2a cos

. ▲

Прямая линия

Общее уравнение прямой. Всякое уравнение первой степени относи-

тельно x и y, т.е. уравнение вида

Ax+By+С=0 (9)

(A, B, C – постоянные коэффициенты, причем A

0) определяет на плос-

кости некоторую прямую. Это уравнение называется общим уравнени-

ем прямой.

Частные случаи

1. C=0; A

0; B

0. Прямая, определяемая уравнением Ax+By=0, прохо-

дит через начало координат.

2. A=0; B

0; C

0. Прямая, определяемая уравнением By+C=0 (или

y=b, где b=-C/B), параллельна оси Ox.

3. B=0; A

0; C¹0. Прямая, определяемая уравнением Ax+C=0 (или

x=a, где a=-C/A), параллельна оси Oy.

4. B=C=0; A

0. Прямая, определяемая уравнением Ax=0 (или x=0, по-

скольку A

0), совпадает с осью Oy.

5. A=C=0; B

0. Прямая, определяемая уравнением By=0 (или y=0, по-

скольку B

0), совпадает с осью Ox.

Уравнение прямой с угловым коэффициентом. Если в общем урав-

нении прямой B

0, то, разрешив его относительно y, получим уравнение вида

y=kx+b (10)

(здесь k=-A/B, b=-C/B). Его называют уравнением прямой с угловым коэффи-

циентом, поскольку k=tg

, где

– угол, образованный прямой с по-

ложительным направлением оси Ox. Свободный член уравнения b ра-

вен ординате точки пересечения прямой с осью Oy.

Уравнение прямой в отрезках. Если в общем уравнении прямой C

то, разделив все его члены на –C, получим уравнение вида

=+ (11)

(здесь a=-C/A, b=-C/B). Его называют уравнением прямой в отрезках; в нем a

является абсциссой точки пересечения прямой с осью Ox, а b – ордина-

той точки пересечения прямой с осью Oy. Поэтому a и b называют от-

резками прямой на осях координат.

Нормальное уравнение прямой. Если обе части общего уравнения

прямой Ax+By+C=0 умножить на число

+±=

BA/1

(которое назы-

вается нормирующим множителем, причем знак перед радикалом нужно вы-

брать так, чтобы выполнялось условие

C<0), то получим уравнение

x cos

+ y sin

– p=0. (12)

Это уравнение называется нормальным уравнением прямой. Здесь p –

длина перпендикуляра, опущенного из начала координат на прямую, а

– угол,

образованный этим перпендикуляром с положительным направлением оси Ox.

Уравнение прямой, имеющей угловой коэффициент k и проходящей че-

рез точку M(x

), записывается в виде

y-y

=k(x-x

). (13)

Уравнение прямой, проходящей через две точки. Уравнение пря-

мой, проходящей через точки M

) и M

), записывается в виде

, (14)

и угловой коэффициент этой прямой находится по формуле

= . (15)

Если x

, то уравнение прямой, проходящей через точки M

и M

имеет вид x=x

. Если y

, то уравнение прямой, проходящей через точки M

и M

, имеет вид y=y

Угол между прямыми. Острый угол между прямыми y=k

x+b

y=k

x+b

определяется по формуле

1 kk

. (16)

Условие параллельности прямых имеет вид k

Условие перпендикулярности прямых имеет вид k

=-1/k

Пересечение прямых. Расстояние от точки до прямой. Пучок пря-

мых. Если A

, то координаты точки пересечения прямых

0CyBxA

111

=++ и 0CyBxA

222

=++ находятся путем совместного реше-

ния уравнений этих прямых .

Расстояние от точки

(

)

y;xM до прямой

находится

по формуле

CBxAx

= (17)

Биссектрисы углов между прямыми 0CyBxA

111

=++ и

0CyBxA

222

=++ имеют уравнения

222

111

CyBxA

. (18)

Если пересекающиеся прямые заданы уравнениями 0CyBxA

111

=++

и 0CyBxA

222

=++ , то уравнение

+++

111

CyBxA

(

)

,CyBxA 0

222

=++ (19)

где

числовой множитель, определяет прямую линию, проходящую через

точку пересечения заданных прямых. Давая в последнем уравнении

различные значения, будем получать различные прямые, принадлежащие

пучку прямых, центр которого есть точка пересечения заданных прямых.

8. Дано общее уравнение прямой

Написать: 1) урав-

нение прямой с угловым коэффициентом; 2) уравнение прямой в отрезках;

3) нормальное уравнение прямой.

∆ 1) Разрешив уравнение относительно у, получаем уравнение прямой

с угловым коэффициентом: .13x)5/12(y -= Здесь

.13b -=

2) Перенесем свободный член общего уравнения в правую часть и раз-

делим обе части на 65; имеем

(

)

(

)

.1y655x6512 =- Переписав последнее

уравнение в виде

( )

5/65

12/65

+ получим уравнение данной прямой в

отрезках. Здесь а = 65/12,

.13

b -=-=

3) Находим нормирующий множитель

.13/1)5(12/1

=-+=

Умножив обе части общего уравнения на этот множитель, получаем нор-

мальное уравнение прямой

)

(

)

(

Здесь

cos

.5p,13/5sin =-=

▲

9. Составить уравнение прямой, проходящей через точку М(-2;-5) и

параллельной прямой 3х+4у+2=0.

∆ Разрешив последнее уравнение относительно у, получим

.2/1x)4/3(y --= Следовательно, в силу условия параллельности угловой

коэффициент искомой прямой равен -3/4. Воспользовавшись уравнением

(13), получаем

[

]

,)(x)/()(y 2435 ---=-- т.е.

▲

10. Даны вершины треугольника: А(2; 2), В(-2; -8) и С(-6; -2). Соста-

вить уравнения медиан треугольника.

∆ Находим координаты середин сторон ВС, АС и АВ:

,/)(x 4262

-=--=

;52/)28(y

-=--= );5;4(A

,22/)62(x

-=-= ;02/)22(y

=-= );0;2(B

,02/)22(x

=-= ;32/)82(y

-=-= ).3;0(C

Уравнения медиан находим с помощью уравнения прямой, проходя-

щей через две данные точки. Уравнение медианы АА

(у-2)/(-5-2)=(x-2)/(-4-2), или 7x-6y-2=0.

Находим уравнение медианы ВВ

. Поскольку точки В(-2;-8) и В

(-2;0)

имеют одинаковые абсциссы, медиана ВВ

параллельна оси ординат. Ее уравне-

ние х+2=0. Уравнение медианы СС

: (y+2)/(-3+2)=(x+6)/(0+6), или x+6y+18=0. ▲

11. Даны вершины треугольника А(0; 1); В(6; 5) и С(12; -1). Составить

уравнение высоты треугольника, проведенной из вершины С.

∆ По формуле (15) найдем угловой коэффициент стороны АВ, имеем

k = (5-1)/(6-0) = 2/3. В силу условия перпендикулярности угловой ко-

эффициент высоты, проведенной из вершины С, равен –3/2. Уравнение этой

высоты имеет вид у+1 = (-3/2)(х-12), или 3х+2у-34=0. ▲

12. Даны стороны треугольника: (АВ): х + 3у – 7 = 0, (ВС): 4х – у – 2 = 0,

(АС): 6х +8у – 35 = 0. Найти длину высоты, проведенной из вершины В.

∆ Определим координаты точки В. Решая систему уравнений х+3у-

7=0, 4х – у – 2 = 0, получим х = 1, у = 2, т.е. В(1;2). Находим длину высоты

ВВ

как расстояние от точки В до прямой АС:

.,BB 31

352816

-×+×

= ▲

13. Определить расстояние между параллельными прямыми

0103yx3 =-+ и .0105y2x6 =++

∆ Задача сводится к определению расстояния от произвольной точки

одной прямой до другой прямой. Полагая, например, в уравнении первой

прямой х=0, получаем

.103y = Таким образом,

(

)

-103;0M точка, лежа-

щая на первой прямой. Определим расстояние от точки М до второй прямой:

.,d 55

102

1011

436

105103206

+×+×

= ▲

14. Даны вершины треугольника: А (1; 1), В (10; 13), С (13; 6). Соста-

вить уравнение биссектрисы угла А.

∆ Пусть D – точка пересечения биссектрисы со стороной ВС. Из свой-

ства биссектрисы внутреннего угла треугольника следует, что

.AC:ABDC:BD = Но

( )

,)(AB 15113110

=-+-=

( )

.)(AC 1316113

=-+-=

Следовательно,

./DC:BD 1315==

Так как известно отношение, в

котором точка D делит отрезок ВС, то координаты точки D определяются по

формулам

6)13/15(13

13)13/15(10

или х = 325/28, у = 259/28, т.е. D = (325/28; 259/28). Задача сводится к состав-

лению уравнения прямой, проходящей через точки А и D:

325

259

т.е.

▲

15. Даны уравнения высот треугольника АВС:

и координаты вершины А(2; 2). Составить уравнения сторон

треугольника.

∆ Легко убедиться в том, что вершина А не лежит ни на одной из за-

данных высот: ее координаты не удовлетворяют уравнениям этих высот.

Пусть

– уравнение высоты ВВ

, и

– урав-

нение высоты СС

. Составим уравнение стороны АС, рассматривая ее как

прямую, проходящую через точку А и перпендикулярную высоте ВВ

. Так

как угловой коэффициент высоты ВВ

равен 3, то угловой коэффициент сто-

роны АС равен –1/3, т.е. ./k

31-= Воспользовавшись уравнением прямой,

проходящей через данную точку и имеющей данный угловой коэффициент,

получим уравнение стороны АС:

(

)

(

)

,2x3/12y --=- или

Аналогично получаем ,1k,1k

ABCC

=-= и уравнение стороны АВ

имеет вид

т.е.

Решив совместно уравнения прямых АВ и ВВ

, а также прямых АС и

СС

, найдем координаты вершин треугольника:

)

;

(

и ).3;1(C - Ос-

тается составить уравнение стороны ВС:

3/2x

3/2y

т.е.

▲

16. Составить уравнения прямых, проходящих через точку М (5; 1) и

образующих с прямой

угол