Куклина Г.Я. Олимпиадные задачи по математике начального уровня для учащихся 9-11 классов

Подождите немного. Документ загружается.

Олимпиадные задачи по математике начального уровня..

Таким образом, из равенства

'" '" "'OA O A AOO AOO=⇒∠ =∠ ⇒

ABC ACO AB AC⇒∠ =∠ ⇒ = ⇒

ABC⇒∆

– равнобедренный (рис. 48).

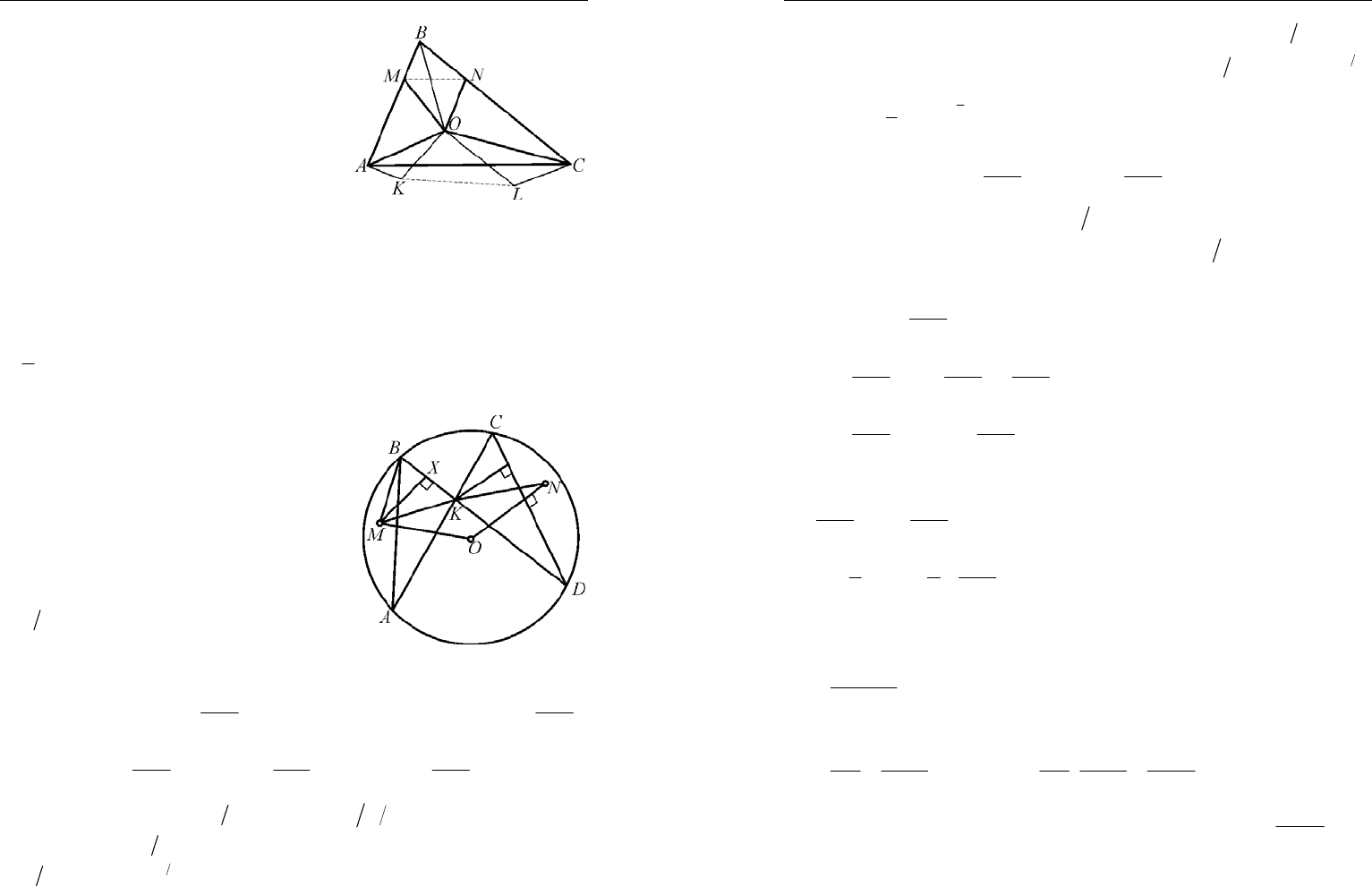
3. Решение. Построим такие точки

K и

, лежащие внутри угла АОС, что

треугольники АКО и ВМО, и треуголь-

ники

;CLO

соответственно рав-

ны. Тогда

;KO OM

;LO ON=

(

)

KOL AOC MOB BOD∠=∠−∠ +∠ =

Рис. 49

MON=∠ ⇒ MNO KOL KL MN∆=∆⇒=⇒

периметр треугольни-

ка

равен

MMNNB

AK KL LC AC=++≥

(рис. 49).

4. Решение. Пусть Х – середина ВК. Тогда

KMX

∠

KMB KAB KDC=∠ =∠ =∠

если

XKD MK⊥⇒⊥CD

если

ON CD⊥ ; ||ON KM

. Аналогично,

||OM KN

. Если точки

,, ,OKM N

не лежат на одной прямой, то получаем

параллелограмм

OMNK ⇒ OM KN=

В противном случае рассмотрим орто-

гональные проекции отрезков

,OM

на АС. Поскольку точки

,,OM N

проектируются соответственно в сере-

дины отрезков АС, АК, КС, то проекции

обоих параллельных отрезков равны

2KC

. Следовательно, равны и длины

самих отрезков (рис. 50).

Занятие 14.

Рис. 50

Решение:

() (()) ,

fx x

ϕ= ⇒ϕ =

-1

1() ,

≠− ⇒ϕ =

−

1x ≠

если

=⇒

()

⎛⎞

⎜⎟

−

⎝⎠

() , 1

fx x

⎛⎞

⇔= ≠

⎜⎟

−

⎝⎠

Решение:

() 1 ,

(

)

(()) 11 () ()

xx x x

−

ϕϕ = = ⇒ϕ =ϕ

Заменяя

x→

из исходного уравнения получаем

(

)

(

)

12 2

fx fx−=⇒

. В совокупности с исходным уравнением

Учебное пособие

имеем систему уравнений

(

)

()

() 2 1 2

12()2

fx f x

fx fx

⎧

−=

⎪

⎨

−=

⎪

⎩

() 2 2

⎛⎞

⇒=−+

⎜⎟

⎝⎠

Решение.

() ;

ϕ=

−

(()) ;

−

ϕϕ =

( ( ( )))

ϕϕ =

. Заме-

няя в заданном уравнении

(

)

x→−

и во вновь полученном

уравнении снова делая ту же самую замену

(

)

x→−

, получаем

систему

() ,

111

() ,

fx f x

ffx

⎧

⎛⎞

⎜⎟

⎪

−

⎝⎠

⎪

−

⎛⎞⎛⎞

⎨

⎜⎟⎜⎟

−

⎝⎠⎝⎠

⎪

−−

⎛⎞

⎪

⎜⎟

⎝⎠

⎩

из трех уравнений относительно трех значений функций

(),

⎛⎞

⎜⎟

−

⎝⎠

−

⎛⎞

⎜⎟

⎝⎠

, решая которую находим искомую функцию:

111

() 1

fx x

⎛⎞

=+−−

⎜⎟

−

⎝⎠

Решение. Прологарифмируем исходное уравнение и выразим

искомую функцию:

(

)

() 1lg ( 1)lg( 1) ()

nnfnn fn

−

=− −⇒ =

lg( 1)

1(1)

−

=+ ⋅ −

. Полагая в последнем равенстве значения

последовательно равными 2, 3, 4, …, получим:

(2) 1f =

(3)f =

lg 2 lg(3!)

lg 3 lg 3

=+ =

lg 3 lg(3!) lg(4!)

(4) 1

lg 4 lg3 lg 4

f =+ ⋅ =

Применяя метод

математической индукции нетрудно показать, что

lg( !)

()

Решение. Полагая

1() (1),

xfyyf=⇒ = ⋅

(1) const

c==⇒

Олимпиадные задачи по математике начального уровня..

()

xcx⇒=⋅.

Решение. Подставляя

0x =

и заменяя у на

(

)

−

получаем

систему из двух уравнений, которую можно решить:

() 2( ) (0) 2() 2

( ) 2() (0) 2( ) 2

fy f y f fy y

fy fy f fy y

−−+ − =−

⎧

⇒

⎨

−− + − −=−−

⎩

если

0 (0) 1 xy f== ⇒ =⇒

()

() (0) 2 () 1

yy f fyy=+ + ⇒ =+

Решение:

(

)

(

)

zy z

efe yfe

⋅

=⇒ =⋅

для

(

)

zfe

⇒=

()yfe cy=⋅ =⋅⇒

ln ( ) ln

eyxfxcx=⇒= ⇒ =

Решение. Заменим х на

(

)

, а у на 0:

()(0)()()

()()

22 2

x y fx y f fx fy

fx y fx

+++ +

⎛⎞

==⇒+=+

⎜⎟

⎝⎠

() .

yc+−

Если

() () ( ) () ()

fx c x y x y

=−⇒ϕ+=ϕ+ϕ

. Это есть

уравнение Коши, оно имеет решение вида

() ()

ax f x ax cϕ=⇒ =+

Решение:

0,m

0 (0 (0)) ( (0)) (0)nfffff

⇒+ = + ⇒

( (0)) ( (0)) (0) (0) 0;ff ff f f⇒=+⇒=

0( (0))nfmf=⇒ + =

(()) (0) () (())ffm f fm ffm=+⇒=⇒

() или

() 0.

fm m

⎡

⎢

⎣

10.

Решение. Подставляя вместо х величину

(

)

−

в исходное

уравнение и рассматривая теперь систему из двух уравнений, мо-

жем найти вид функции:

()

2() (1 )

() 2 1

2(1 ) () (1 )

fx f x x

fx x x

fxfx x

⎧

+−=

⎪

⇒=+−

⎨

−+ =−

⎪

⎩

Занятие 15.

Решение. Строгая монотонность функции

32 2xx=⇒+ =⇒

если

1 2;xxx<⇒+ <

если

x>⇒ +

21xx+>⇒=

Решение. Если 00sin

<⇒< <. Поскольку косинус

является убывающей функцией на данном промежутке, то

cos cos(sin )

. Поскольку синус является возрастающей функци-

Учебное пособие

ей там же, то для

[]

cos 0,1 0, sin sin(cos )

tx tt x

⎡⎤

∈⊂ ⇒<⇒ <

⎢⎥

⎣⎦

cos cos(sin )

x<<

Решение:

1( ) 1()

(2) 1 :

1( ) 1()

xk fx

fx k

xk fx

⎛⎞

++ +

+⋅ = = +

⎜⎟

−+ −

⎝⎠

1() 1 1

:1 ( 4 ) () 4.

1() () (2)

xk fxTk

fx fx fx k

⎛⎞

−=−⇒+⋅=− =⇒=

⎜⎟

−+

⎝⎠

Решение. Пусть Т – искомый период, тогда

tg(sin )

tg(sin( ) (*) xT=+⇒

sin( ) sin 2sin cos

TxT

xT k x

⎛⎞

=π+ ⇒ =

⎜⎟

⎝⎠

k=π

. Поскольку это равенство верно для любого х, возьмем

0x =

[

sin 0 sin 0 ,Tkk T Tn

π⇒ =⇒ =⇒ =π

или

. Проверкой

убеждаемся, что подходит только последнее значение, или из соот-

ношения (*) при

следует, что

sin sin( ) 2xxTT

+⇒=π

Занятие 16.

Решение. Достаточно доказать, что каждый столбец можно

сделать нулевым. Действительно, вычитание 1 из всех чисел одного

столбца не влияет на другие столбцы, а удвоение чисел одной стро-

ки не влияет на нулевые столбцы и оставляет натуральными числа в

остальных столбцах. Пусть есть некоторый столбец из натуральных

чисел. Будем вычитать по 1 из всех

его чисел, пока не появятся еди-

ницы. При этом сумма чисел столбца уменьшится. Если не все чис-

ла столбца равны 1, то удвоим те строки, в пересечении которых с

нашим столбцом стоят 1, а затем вычтем из всех чисел столбца по 1.

Эта операция, очевидно, равносильна вычитанию 1 из всех чисел

столбца, больших 1. Проделав

ее несколько раз, получим столбец,

состоящий из одних 1. Вычитая из чисел этого столбца 1, получим

столбец из одних нулей. Далее можно операцию повторить для всех

остальных столбцов.

Решение. Выберем произвольно

(3 2)n

−

участника анкеты и

разобьем их на

(3 2)n

−

группы по одному человеку в каждой. Ос-

тавшихся будем последовательно помещать каждого в группу, все

люди которой имеют с ним различные вкусы. Такая группа всегда

существует, так как у каждого человека общий любимый компози-

тор с

(1)n

−

человеком, художник – с

(1)n

−

человеком и писа-

Олимпиадные задачи по математике начального уровня..

тель – с

(1)n −

человеком, то есть общие хоть в чем-то вкусы не бо-

лее, чем с

3( 1) 3 3nn−= −

людьми, а групп

(3 2)n

−

. Следовательно,

всегда существует группа, в которой нет людей, вкусы которых пе-

ресекаются со вкусами этого человека, и куда его можно поместить,

не нарушая требований условия задачи. Таким образом, мы можем

разместить всех участников по

(3 2)n −

группам в соответствии с

требованиями задачи.

Решение: а) если все прямые параллельны друг другу, то они

делят плоскость на

(1)n

областей. При этом все области не могут

быть окрашены, тем самым число окрашенных областей не превос-

ходит

. Утверждение верно, так как

121

333

nn n

nnn

+++

⋅≥⋅=

;

б) пусть теперь не все прямые параллельны друг другу. Граница ка-

ждой области состоит из нескольких отрезков и лучей, принадле-

жащих разным прямым. Эти отрезки и лучи назовем сторонами об-

ласти. Каждая область имеет не менее двух сторон. Через

обозначим число окрашенных областей, имеющих две стороны, че-

рез

обозначим число окрашенных областей, имеющих три сто-

роны, и так далее. Наконец, через

обозначим число окрашенных

областей, имеющих максимальное число сторон. Покажем, что

mn≤

. Граница любой области с двумя сторонами состоит из двух

лучей, причем каждый луч может лежать на границе только одной

из окрашенных областей. Число всех таких областей не превосходит

, не более двух на каждой прямой. Следовательно, общее число

сторон окрашенных областей с двумя сторонами не превосходит

или

mn≤

. Каждая из

прямых разбивается остальными не более,

чем на

частей, отрезков или лучей. Поэтому общее число всех

частей не превосходит

. Каждая из частей является стороной не

более одной из окрашенных областей. Следовательно, общее число

сторон таких областей не превосходит

2 3 ...

nmm kmn⇒+++≤

Число окрашенных областей равно

...

mm m+++

. Используя до-

казанные выше неравенства, находим, что

223

2 3 ...

...

33333

mmm kmnnnn

mm m

+++ +

+++≤ + ≤+=

Решение. Утверждение задачи следует из двух замечаний.

Учебное пособие

1. Если внутренний узел квадрата переходит в граничный узел

прямоугольника, то его четыре соседа (по горизонтали и вертикали)

также переходят в граничные узлы прямоугольника, причем на той

же стороне (исходный узел не мог перейти в угол). Это сразу следу-

ет из того, что взятый узел и его соседи – это центр и

вершины

квадрата со стороной

и площадью 2.

2. Если

≠

, то у квадрата внутренних узлов больше, чем у

прямоугольника. Действительно, у квадрата их

(2)n −

, у прямо-

угольника

( 2)( 2) ( 2) ( 2)( 2) 2( 2 ),ab n ab abn−−⇒−−−−=+−

2ab n+>

, так как при постоянном произведении

ab n=

сумма

минимальна, когда сомножители равны. Итак, если

ab≠

, то суще-

ствует внутренний узел квадрата, которому соответствует гранич-

ный узел прямоугольника, а тогда, применяя много раз случай 1),

получим, что все узлы квадрата перешли в узлы одной стороны

прямоугольника, что невозможно. Поэтому,

Решение. Легко проверить, что множество

{

1,2,3,5,10,20,25,

}

50,100

из 9 элементов удовлетворяет условию задачи. Покажем,

что меньшим числом элементов обойтись нельзя. Расположим эле-

менты произвольного множества, удовлетворяющего условиям за-

дачи, в монотонном порядке:

1 ... 100

aa a

<<<=

. По условию

при любом

1k >

справедливо равенство

;

kpq

aaa

qk<⇒

−

⇒≤

. Но для всех значений

равенства

−

не могут

быть выполнены, так как 100 не является степенью двойки. Таким

образом, хотя бы для одного

≤

выполнены неравенства

12 2

kk k k

aa a a

−

−−

≤

+≤

. Теперь запишем

100 2 2 ...

nn n

aa a

−−

≤≤⋅≤

232 32 ..

nk nk nk

kk k

aa a

−− −+

−−

≤⋅≤⋅⋅≤⋅ ⋅≤

−

≤

⋅⋅⇒

n−

≥

100

(2 64) 3 6 9

nn≥=⇒−≥⇒≥. Существует много других

примеров нужных множеств. Таковыми являются, например, мно-

жества

{

}

1,2,4,6,10,20,30,50,100 ;

{

}

1,2,4,8,16,32,64,100

Олимпиадные задачи по математике начального уровня..

Занятие 17.

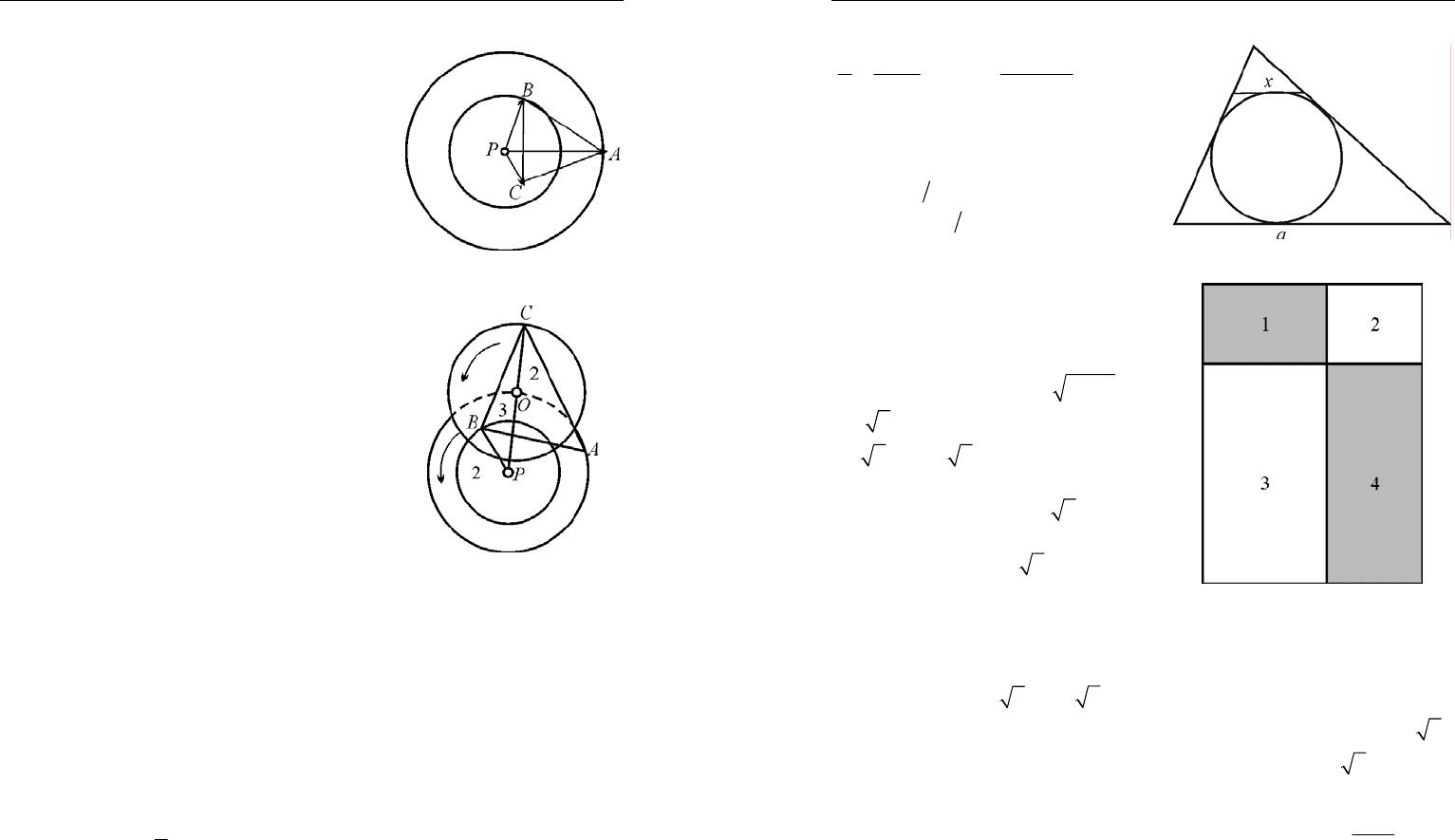
1. Решение. Можно рассмотреть две

концентрические окружности

,SS

центром в точке Р и радиусами 2 и 3 соот-

ветственно. Точка А будет лежать на

, и

ее положение можно, без ограничения

общности, зафиксировать. Точка В будет

лежать на окружности

, ее положение

можно сделать переменным, т. е. заста-

вить точку В «обежать» окружность

Можно доказать, например, при помощи

векторов, что при обегании точкой В ок-

ружности

точка С будет перемещаться

по окружности радиусом 2 с центром в

фиксированной точке О, удаленной от

точки Р на расстояние 3. Из этого факта

будет следовать оценка

5PC ≤

(рис. 51,

52).

2. Решение. Покажем, что это число

равно 5. На 5 тетраэдров куб разбить лег-

ко. Можно, например, отсечь от куба

''' 'ABCDA B C D

четыре угловых тетраэд-

ра

''',AABD

''',CCBD

BAC

'DD AC

Рис. 51

Рис. 52

Труднее показать, что куб нельзя разбить на меньшее число тетра-

эдров. Пусть куб разбит на тетраэдры. Тогда имеется по крайней

мере два из них, основания которых должны лежать на основании

ABCD

куба, так как грань куба – квадрат и не может быть целиком

гранью одного тетраэдра. Аналогично имеются, по крайней мере,

два тетраэдра, основания которых лежат на верхней грани куба. Эти

тетраэдры отличны от первых двух, так как тетраэдр не может

иметь двух параллельных граней. Сумма объемов этих тетраэдров

не превосходит

, следовательно, они не могут заполнять весь

куб. Таким образом, наименьшее число тетраэдров равно 5.

3. Решение. Пусть х – длина искомого отрезка, а – длина основа-

ния треугольника. В силу того, что отрезки касательных равны, пе-

риметр маленького треугольника, отсекаемого касательной, равен

Учебное пособие

2( )

−

, и в силу подобия треугольников получаем

xpa

−

=⇒

()ap a

−

. Вели-

чина а может принимать все зна-

чения между 0 и р, максимум этого

квадратного трехчлена достигается

при

2ap

, величина отрезка при

этом равна

(рис. 53).

4. Решение. Допустим, что пря-

моугольник, изображенный на

рис. 54, удовлетворяет условию

задачи, т. е.

1,S ≥

2,S ≥

1S ≥

. В силу того, что

⋅

23 1 4 14

22SS S S SS=⋅≥⇒+≥ ⋅≥

22≥⇒

1234

12SSSS

++≥++

22 3 22+=+

. Поэтому длины

незаданных сторон прямоугольни-

ка не меньше, чем

322+

. С дру-

гой стороны, прямоугольник со

сторонами 1 и

322+

удовлетво-

ряет условию задачи, так как обла-

дает необходимым для этого раз-

биением на прямоугольники.

Для

Рис. 53

Рис. 54

этого прямоугольник, площадь которого равна

, надо взять со

сторонами

22,a =−

21b

. Тогда размеры остальных сторон

прямоугольника однозначно определяются. Имеем

2;SS==

1;S

. Следовательно, искомая длина равна

322+

Занятие 18.

1. Решение. По теореме синусов в треугольнике АМВ

sin

где

– радиус круга, описанного около треугольника АМВ (рис. 55).

Поскольку отрезок АВ задан, то требование того, чтобы угол был

наибольшим, сводится к требованию того, чтобы радиус был наи-

меньшим. Центр описанной окружности, точка О лежит на перпен-

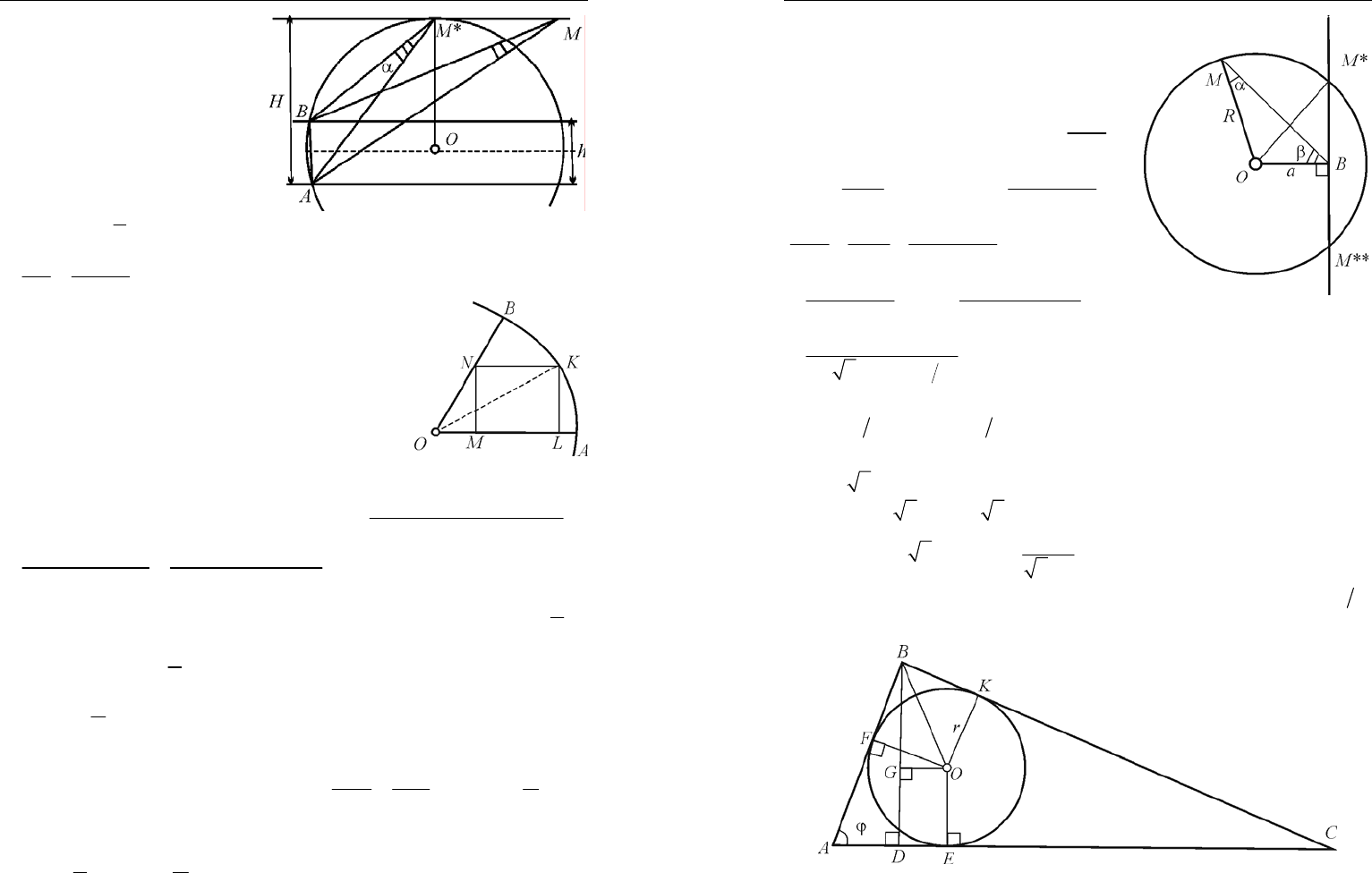
Олимпиадные задачи по математике начального уровня..

дикуляре к середине отрезка

АВ, этот перпендикуляр па-

раллелен заданным прямым.

Радиус равен отрезку ОМ, он

будет наименьшим, если ОМ

перпендикулярен третьей пря-

мой, причем

OM OB OA

Тогда получаем

sin

=−⇒ α=

Рис. 55

AB h

−

2. Решение. Пусть

KLMN

– указанный пря-

моугольник (рис. 56). Положим

;OA OB R==

sinAOK KL MN R∠=ϕ⇒==ϕ

;

OL =

cos ctg sin ctgROMMNR=ϕ⇒= α=ϕα⇒

(

)

cos sin ctgML NK OL OM R==− = ϕ−ϕ⋅α⇒

(

)

sin cos sin ctg

KLMN

SR=ϕ⋅ϕ−ϕ⋅α=

A⋅

Здесь исследованию подлежит выражение А.

Рис. 56

Преобразуем его:

cos sin sin cos

sin

⋅α−ϕ⋅ α

=ϕ⋅ =

sin sin( ) cos( 2 ) cos

sin 2sin

ϕ⋅ α−ϕ α− ϕ − α

αα

. Выражение принимает наи-

большее значение, когда

cos( 2 )α− ϕ

наибольший. Поскольку

−

2cos(2)

<−ϕ<α− ϕ<α≤ ⇒ α− ϕ

максимальный, когда

−ϕ=

=⇒ϕ=

3. Решение. Пусть М – произвольная точка окружности. По тео-

реме синусов для треугольника ОМВ:

sin sin

⇒

αβ

sin sin ,

=β

sin 1β≤

. Поэтому

sin 1

≤

, равенство достигается, когда

sin 1

=⇔

sin

β=β = ⇒ α=

При этом получаем две точки М такие, что

Учебное пособие

хорда, их соединяющая, перпендикулярна

ОВ (рис. 57).

4. Решение. Имеется 2 решения.

1 решение. Метод площадей:

;

AOB BOC AOC ABC

SSS S

;

sin

AB =

;

cos

BC =

sin cos

⇒

ϕ⋅ ϕ

sin cos sin cos

rh rh rh

ϕϕ⋅ϕ

sin cos

=⇒

ϕ⋅ ϕ

1sin cos

ϕ+ ϕ

Рис. 57

()

12sin 4

+ϕ+π

Последняя дробь принимает наименьшее значение, когда

(

)

sin 4 1 4

+π = ⇒ϕ=π

2 решение. Четырехугольник

KOF

– квадрат, поэтому

Or=

. Ломаная ВОЕ состоит из двух звеньев: ВО и ОЕ, ее дли-

на равна

2(21) ;rrr BGBO+= + ⇒ ≤

GD OE BD BO

⇒≤+

OE+⇒ (2 1)

hr r≤+⇔≥

. Минимальным значение будет,

когда высота

совпадает с биссектрисой ВО, при этом

4ϕ=π

(рис. 58).

Рис. 58

Олимпиадные задачи по математике начального уровня..

Занятие 19.

Решение. Предположим, что последние трехчлены не имеют

корней. Тогда их дискриминанты отрицательны:

(2)4p

−

−=

40pp=−<

40qq

−

< . Сложив эти неравенства, получаем:

440pq pq+− −<

. С другой стороны, дискриминанты первых за-

данных многочленов должны быть неотрицательны, то есть

22 22

40& 4 0 440pq q p pqpq−≥ −≥⇒+−−≥

. Получаем противо-

речие.

Решение. Тройка чисел (3; 4; 5) является решением системы

10,

210.

−+=

⎧

⎪

−+=

⎨

⎪

−+=

⎩

Если бы многочлены

,,PQR

существовали, то при подстановке

указанных значений переменных в данное тождество мы бы полу-

чили неверное равенство:

Решение. Так как уравнение

()

xx=

не имеет корней, это

означает, что график функции

()yfx=

, парабола, лежит либо выше,

либо ниже прямой

. Покажем, что в этом случае график функ-

ции

(())yffx=

также лежит либо выше, либо ниже прямой

Пусть

()

xx>

при любом х. Подставляя в это неравенство вместо х

величину

()

, получаем

(() () (())

fx fx x f fx x>>⇒ >

. Это

означает, что график функции

(())yffx=

лежит выше прямой

yx=

. Аналогично можно показать второе неравенство.

Решение. Подставив в данное равенство

12x

, получим

20 10

111 1

00.

242 2

ab pq ab

⎛⎞⎛ ⎞

−+=++≥⇒+=

⎜⎟⎜ ⎟

⎝⎠⎝ ⎠

Равенство теперь

можно переписать в виде:

(

)

()( )

20 20

21 2xpxq x bxb++ = − − − =

()

(

)

211

b=− −

. Приравнивая в получившемся равенстве коэф-

фициенты при

, найдем

(

)

20 20 20 20

11 2 2 1bb=− ⋅ ⇒=± −

. Теперь

равенство принимает вид:

Учебное пособие

()

20 2

222

111

224

xpxq x xpxq x xx

⎛⎞ ⎛⎞

+=− ⇒++=−=−+⇒

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

1;p⇒=−

⇒

20 20

21;a

⎡

±−

⎣

20 20

21;b

−∓

1;p

− 0q =

Решение. Индукцией по

докажем, что для любого

сумма

...

Saa a

+++

представима в виде

(1),

bZ∈

. База ин-

дукции:

11 11

001

aa Sa

⇒===⋅⋅ или

112

== ⋅⋅ . Ин-

дуктивный переход:

()()

(

)

222

11 1 1 1 1

... 2

nnnnnnnnn

Sa aa Sa SSaa

+++++

=+++ =+ =+ ⋅ +

()

333 323

11 1 1 1 1 1

... ... 2

nnn nnnnnn

Sa aa a aaSa Sa

++ +++

++ + = ++ + = + ⇒ ⋅ +

+= ⇒

11 11

(1)

2(1)0

1 ( 1)( 2),

или (1).

nnn

nn n nn n n

nn n n n

nnn nn

aSS

Sa a bb a a

ab S b b

abS bb

++ ++

⎡

=⇒ = =

⎢

=⇒ ++−=⇒

⎢

=+⇒ = + +

⎢

=− ⇒ = −

⎢

⎣

Ясно теперь, что все члены последовательности – целые числа.

Решение. Из определения дробной части следует, что

0101

x≤<⇒≤<

. Кроме того, равенство

{

}

ab a

выполняется

только когда b – целое число. Поэтому из равенства

{

}

(

)

(

)

32 3 2 2

331 33 ()33 .

xx x xxZyx xxn

++=⇒ + ∈⇔ = + =

Функция

() 3 3yx x x

возрастает на отрезке

[

]

0;1 ,

(0) 0;y =

3912

(1) 0 6 3 3 0 ,

yb n xxn x

−+ +

=⇒≤<⇒ + −=⇒=

0, 1,n =

2, 3, 4, 5 , 0,x

Решение. Пусть

– общий корень. Тогда

()0fx =

(( )) 0ffx

. Подставив первое равенство во второе, получаем

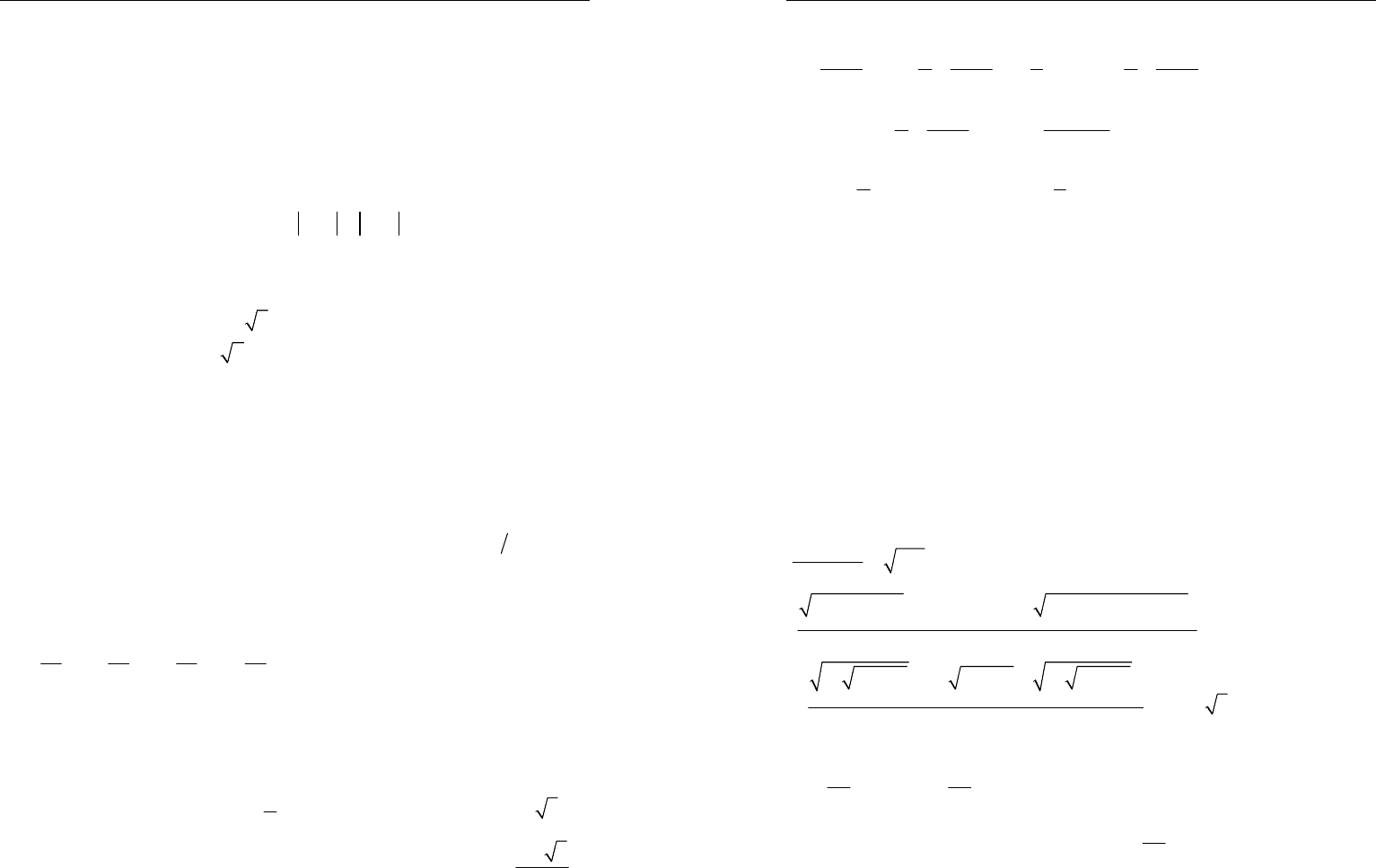
Олимпиадные задачи по математике начального уровня..

(0) 0 0 ( )

bfxxax=⇒=⇒ = + ⇒

(()) 0ffx

⇔

() 0,

() .

⎡

⎢

−

⎣

Тогда условие выполняется, если либо

, либо

≠

()

xa=−

не имеет корней. Получаем, что в первом случае

во втором –

04a<<

. Ответ: 0;b =

04a≤<

Занятие 20.

Решение. Умножим обе части уравнения на

2( 1)( 1)xx

+− −

получаем

()()

64 64

110110xx xxx+−−=⇔+=−⇒=.

Решение. Заметим, что

()

() 6 6 ( ())fx x f fx=+ −⇒ =

(6)6x=+ −

( ( ( ))) ( 6) 6fffx x=+ −⇒ ( ( ( ( ( )))))fffffx

(6) 60 6 6xx=+ −=⇒=−±

Решение. Если

21(1)2xx

−⇒ + = ⇒

3310xxx

+−=

Используя последнее равенство, свернем выражение для функции

(

)

1999 1998 1997 1996 1997 1996 1995 1994

( ) 3 3 3 4 2 ...fxxxxxxxxx=++−+++++

(

)

1996 3 2 1995 1994 1995

1 3 3 1 3 4 ... 1xxxx x x x+= + + − + + + + +=

(

)

1994 3 2 1995 1994 3 2

3 3 1 3 ... 1 3 3 1 2 2.xxxx x x xxx= + +−+ + ++=+ +−+=

Решение. Поскольку нулевым решение быть не может, пусть

х будет одним из корней уравнения, тогда другой будет

. Полу-

чаем систему уравнений, которая может быть решена следующим

образом:

643 2

516 334080

1111

516 334080

xxxx

⎧

−−−+=

⎪

⇒

⎨

⋅−⋅−⋅−⋅+=

⎪

⎩

643 2

6432

516 334080

840331650

xxxx

⎧

−−−+=

⎪

⇒

⎨

−−−+=

⎪

⎩

Вычтем из первого уравнения второе

642

3242430xxx−+−=

и по-

делим на

, получим:

(5)0 0;tx tt t

−⇒ −=⇒=

2,3

±⇒

Вычисляя значения х и делая проверку, получаем ответ:

Учебное пособие

Решение:

cos sin sin

2007 2 2007 2 2 2007

xx x

ππ

⎛⎞

⎛⎞ ⎛⎞

−⇒= − =

⎜⎟ ⎜⎟

⎜⎟

⎝⎠ ⎝⎠

⎝⎠

2008 1

sin 2007 sin

22007 2

π−

⎛⎞

⎛⎞⎛ ⎞

=−=π−=

⎜⎟⎜ ⎟

⎜⎟

⎝⎠⎝ ⎠

⎝⎠

sin cos 2 , .

xx kkZ

⎛⎞

=−−=− ⇒=±π+π ∈

⎜⎟

⎝⎠

Решение. В левой части уравнения 2011 слагаемых, среднее

из них равно

()

1005x +

. После замены переменной

1005tx=+

уравнение примет вид:

()()()

555

1005 ... 1 1tttt

−

++− +++ +

()

... 1005 0t++ =

. Сумма равноудаленных от среднего слагаемого

t слагаемых равна

()()

() ,

ttk tk=− ++

1,2,...,1005k

. Ясно,

что

() 0

ft>

0t >

() 0

для

() 0

если

0t =

. Зна-

чит единственный корень уравнения

0 1005tx

⇒=−

Занятие 21.

Доказательство. Дважды применим неравенство (2):

4442222222 2 2

()a b c a b b c a c a bc ab c abc abc a b c

+≥ + + ≥ + + = ++.

Доказательство. Используя несколько раз неравенство

xyz

≥

, получаем:

(

)

222 222222

abcabbcac abbcac

abc

++⋅ +++ + +

≥

222 222 444

33 3

3(1 3)

abc abc abc

abc

⎛⎞

⋅⋅⋅+⋅

⎜⎟

⎝⎠

≥=+

Доказательство. Докажем равносильное неравенство:

111

⎛⎞⎛⎞

+≥+−

⎜⎟⎜⎟

⎝⎠⎝⎠

. Из тождеств (бином Ньютона)

()

x±=

1...,0,

nx a x a x a=± + ± + ≥

если

следует, что

()

x+−

Олимпиадные задачи по математике начального уровня..

()

1 2 2 2 ... 0

xnxaxax−− − = + +≥⇔

111

⎛⎞⎛⎞

+≥+−

⎜⎟⎜⎟

⎝⎠⎝⎠

Доказательство. Поскольку выражение

333

Sa b c

+++

3()()()abc ab a b bc b c ac a c+− +−+−+

симметрично относительно

всех переменных, без ограничения общности можно считать, что

0>≥≥ cba

. Так как

(

)

33 2

()()() & a b abab abab+− + =+ −

3()()()()()abc bc b c ac a c c a c b c c a b+−+−+=−−−−

, то исходное

выражение равно

()()()()()Sabab cacbccab

+−+−−−−=

()( )()()0ab abc cacbc=− +−+ − −≥

Доказательство. Приводим выражение к общему знаменате-

лю и преобразовываем:

(

)

22222 2

4 ab ba bc cb ca ac+++++ ≥

(

)

22222 2

32abcabbabccbcaac≥++++++⇔

()()ba c ab c

−

+−+

()0cb a+− ≥

Доказательство:

(

)

22 22 22 22

()(2) 4()48Px y P xy x y x y xy xy+− =+ − +− +=

(

)

(

)

22 2 2 2

4( ) ( ) ( ) 4 0x y xy xy xy=− −−=− +−≥

для

()2xy

≥

Доказательство. Пусть

. Тогда исход-

ное неравенство равносильно следующему:

2ab

≤

. Его спра-

ведливость следует из того, что

2ab+≤

. Действительно,

ab+≤

22ab≤⋅+≤

Решение. Не существует. От противного, пусть такая функция

существует. Положив

() 2 2 () 0.

xy f f

=⇒ π+<⇒ π< В то же

время, если взять

() 2 2 () 0

yf f

=⇒ π−<⇒ π>

. Полу-

чаем противоречие.

Занятие 22.

Решение. Замена переменных позволяет заметить следующее:

;

a=+

;

yb=+

zcabc

+⇒++=⇒

222

xyz

+=⋅+

Учебное пособие

()

222

abc a b c++++++≥.

Решение. Замена переменных

;

;ybc

zac=+⇒

113

3(63)

222

xyxzyz

yxzxzy

⎛⎞

= +++++− ≥ −=

⎜⎟

⎝⎠

Доказательство: 2 способа: а) Если положить замену

11 2 2

22 2

...

ab ab ab

aa a

+++

=− ⇒

+++

()

11 2 2

...

ab ab ab

++ ≤

(

)

(

)

22 222 2

12 12

... ...

aa abb b≤+++ +++

()( )

... 0

xa b xa b

⇔

+++ + ≥

б) Введем векторы

{

}

,...

aaa=

{

}

,...

bbb tR

⇒∀ ∈ ⇒

(

)

(

)

(

)

(

)

,0,,2,a tb a tb a tb a tb a tb a a t a b⇒− − =− ≥⇒− − = − +

(

)

(

)

(

)

(

)

(

)

(

)

(

)

,0 , ,,0 , ,,t bb D ab aa bb ab aa bb+≥⇔=− ≤⇒≤

Это и есть требуемое неравенство.

Доказательство:

+≥+

,0ab>

aa bb⇔+≥

(

)

abab≥+ ⇔

(

)

(

)

0.abab

−≥

Доказательство. Замена переменных:

;

bca

+−

;ycab=+− ;

zabc a

=+−⇒= ;

⇒

(222)3

xyzxyz

yxxzzy

⎛⎞

= +++++ ≥ ++ =

⎜⎟

⎝⎠

Доказательство:

,, 0 ,, sin ,

yz xyz a x

∃≤≤⇒=



sin ,by=

sin ;cz=

так как

cos cos 0

=α>,

если

<α< ⇒

(1 )(1 ) (1 )(1 ) (1 )(1 ) 1 ab c ba c ca b abc

−

−+ − −+ − −≤+ ⇔

sin cos cos sin cos cos sin cos cos 1xyz yxz zxy

⋅

⋅+⋅⋅+⋅⋅ <+

sin sin sin

yz+⋅⋅

Докажем последнее неравенство. Так как

(

)

sin( ) 1 sin ( ) sin cos( ) cos sin( )

yz xy z z xy z xy

+≤⇒ ++= ++ + =

sin (cos cos sin sin ) cos (sin cos sin cos ) 1zxy xy zxy yx=−++≤.

Олимпиадные задачи по математике начального уровня..

Перенося слагаемое со знаком минус вправо, получаем требуе-

мое неравенство.

Доказательство. Заметим, что

4 3 1 ( 1)(2 1) 0,xx x x−+=+ − ≥

1x∀≥−

. Выпишем такие выраже-

ния для каждого значения переменной и сложим их, используя ус-

ловие, что сумма кубов равна нулю:

xn x

−+≥⇒≤

∑∑

Доказательство. По неравенству о среднем арифметическом

и среднем геометрическом

bc ac bc ac

ab ab

⎛⎞

+≥⋅=

⎜⎟

⎝⎠

ac ab

⎛⎞

+≥

⎜⎟

⎝⎠

bc ab

⎛⎞

≥

⎜⎟

⎝⎠

Сложив эти три неравенства, получаем требуемый результат.

Занятие 23.

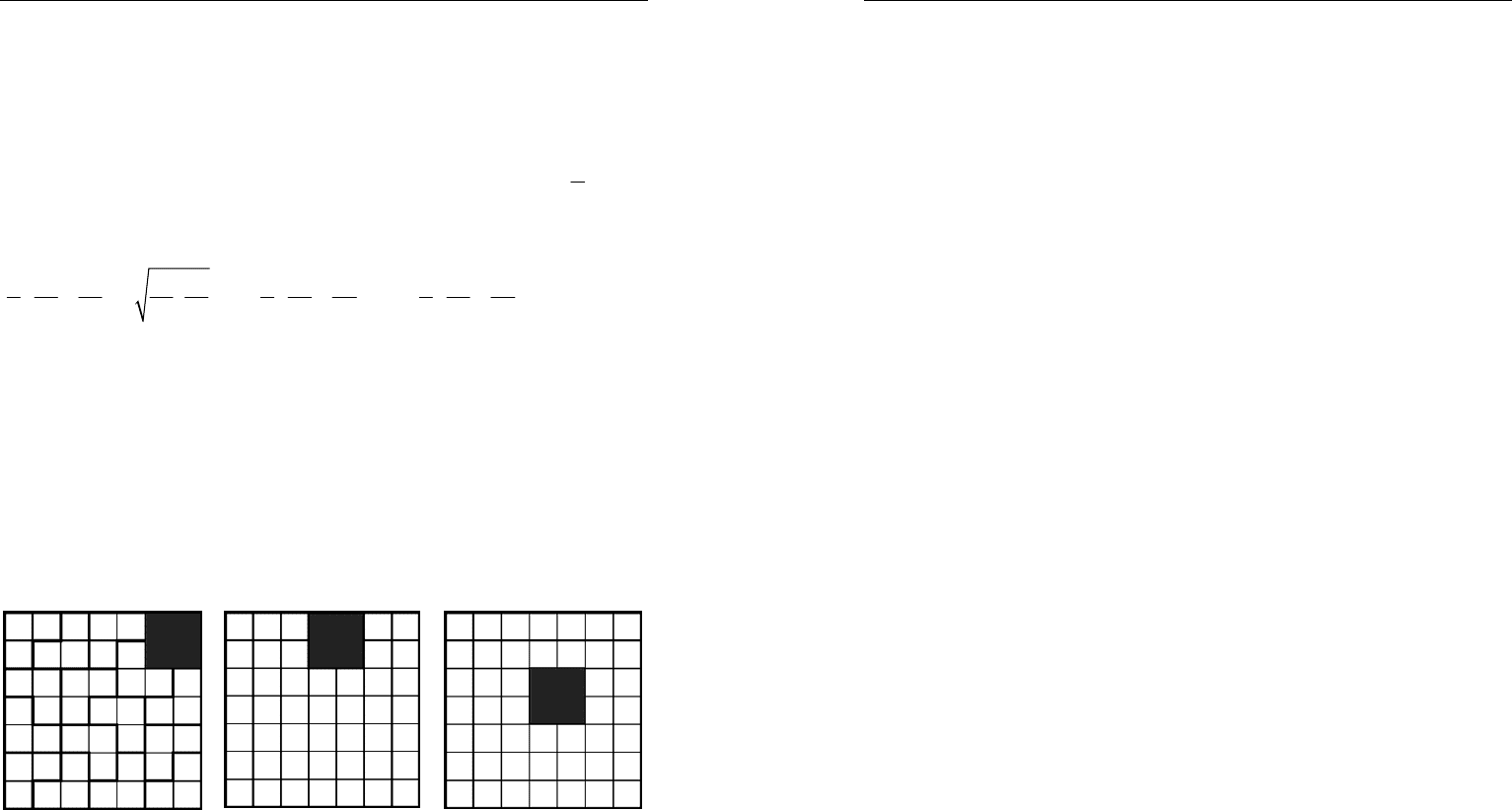
Доказательство. Поскольку

2011 6 335 1=⋅ +

, требуемое ут-

верждение будет доказано, если мы докажем утверждение задачи

для квадратов размером

(6 1) (6 1)nn+× +

индукцией по

∈

. Сна-

чала докажем, что утверждение справедливо при

для квадрата

77×

. Действительно, из соображений симметрии следует, что дос-

таточно рассмотреть только случаи, когда вырезанная клетка лежит

в одном из квадратов

, закрашенных на рис. 59–61, где показа-

но, как разрезать оставшуюся часть.

Рис. 59

Рис. 60

Рис. 61

Пусть утверждение доказано для некоторого значения

∈

Докажем его для квадрата размером

(

)

(

)

67 67kk+× +

. Для этого в

одном из углов данного квадрата поместим квадрат размером

(

)

(

)

61 61kk+× +

, покрывающий вырезанную клетку и удовлетво-

Учебное пособие

ряющий предположению индукции, оставшуюся же часть разрежем

на прямоугольники размером

, а затем и на уголки.

Решение. Пусть числа

, mn

, удовлетворяют

условию задачи. Тогда они имеют одинаковое число цифр, следова-

тельно,

10k

≠

и справедливо неравенство:

(

)

10 1 1

. Слу-

чай

2mn

невозможен, так как тогда

21 1

nm k≥+⇒+≥

(

)

21 21 2

mmmmmm

kkkkkk

≥>>+= +

. Поэтому

10 1

⇒+=

k=+

, что противоречит неравенству

. Поэтому

2mn≥⇒

(

)

(

)

111 110

nn n m m n m

mnm k k k k

−−

⇒≥−⇒ +> − +⇒ −<

k <

так как

≠

. Так как число

(

)

(

)

119

kk+− +



; т. е. кратно 9,

поскольку суммы цифр этих чисел равны, то



, поскольку

−

. В случае

61knm≥⇒− =

– число, имеющее

столько же цифр, сколько и число

(

)

(1) 1

−

, меньшее числа

, начинается с цифры 1, а, значит, число

этой цифрой

кончается, что невозможно, так как

10k

. Остается единственная

возможность:

33,km

⇔=

Доказательство. При

утверждение справедливо. Дей-

ствительно, всего имеется четыре натуральных числа, не превосхо-

дящих

3! 6 3 2 1;

⇒=+

431;

532;

6321

и все они

представимы требуемым образом. Предположим, что утверждение

справедливо для

. Докажем, что в таком случае оно справед-

ливо и для

1nk

. Пусть дано произвольное натуральное число

(

)

1!mk≤+

. Разделив

на

(1)k

с остатком, получим

(

)

1,mk dr=+⋅+

0 rk

≤

. По предположению индукции

существуют различные делители

, ,..., ;

dd d

≤

числа

такие,

что

(

)

(

)

(

)

112

... 1 1 ... 1

dd d mkdkd kdr

++ ⇒ = + + + ++ + +

–

искомое представление числа

. Действительно, в сумме

k+≤ +

слагаемых, все они различны и являются делителями

числа

(

)

1!k

. Последнее слагаемое меньше остальных и является

делителем числа

(

)

1!k

, так как

1rk

Доказать, что оставшуюся часть можно разрезать на уголки из

Олимпиадные задачи по математике начального уровня..

трех клеток. Доказательство. Верно для любого квадрата размером

. Проверка по индукции.

Доказательство.

211

222

mn m n

+− − −

=⋅≥

Занятие 24.

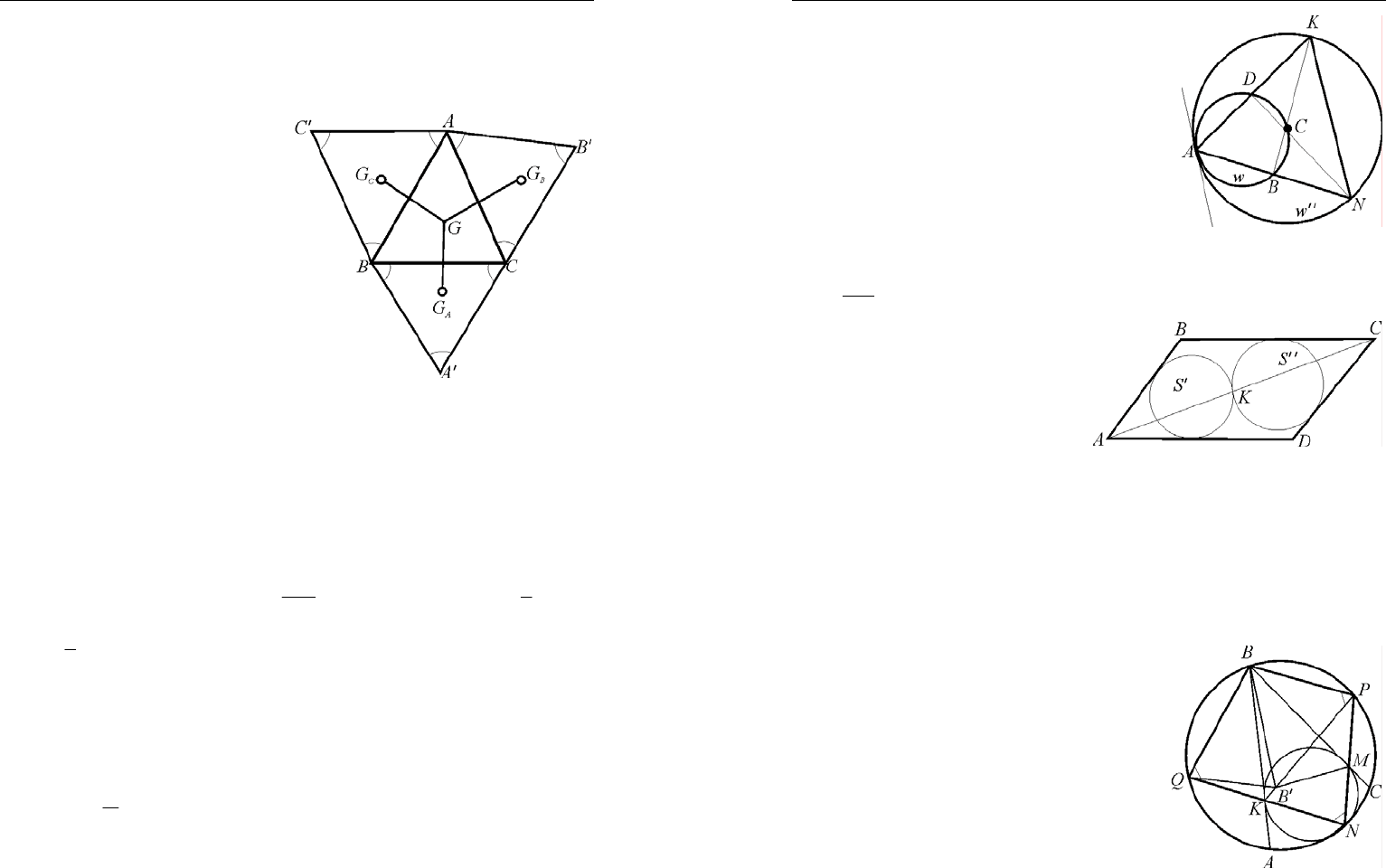
Решение. Приведем дока-

зательство для случая остро-

угольного треугольника (осталь-

ные случаи – самостоятельно),

рис. 62. Вначале покажем, что

отрезки

',AA

B 'CC

равны,

и угол между любыми из них

равен 60

. При повороте вокруг

точки А на угол в 60

отрезок

'AC

переходит в АВ, а отрезок

АС – в

'AB

. Поэтому отрезок

'CC

переходит в отрезок

. Значит,

''CC BB

и угол

Рис. 62

между этими прямыми равен 60

. Аналогично,

''CC AA

''AA BB=

, и углы между всеми отрезками равны 60

. Пусть

ABC

GGG

– центры равносторонних треугольников

'ABC

'CAB

соответственно. При центральном подобии с центром в сере-

дине стороны АС и коэффициентом 1/3 точка В переходит в точку

, а точка

G→

. Поэтому прямые

либо параллель-

ны, либо совпадают и

. Аналогично,

GG AA=

GG CC GG=⇒

равны между собой и образуют

углы в 120

. Поэтому треугольник

ABC

GGG

– равносторонний, а

точка

– его центр.

2. Решение. Пусть окружность

''w

касается окружности

в точ-

ке А (рис. 63). Тогда гомотетия

с центром в точке А и коэффици-

ентом

переводит

''ww→

. Следовательно,

() ,

() ||

BN KNDBKNkDB=⇒ ⇒ =⋅

. Тогда гомотетия

с цен-

тром С и коэффициентом

'kk

−

переводит треугольник

∆

Учебное пособие

в треугольник

CKN

∆

и, следовательно,

переводит окружность, описанную

вокруг первого треугольника в окруж-

ность, описанную около второго тре-

угольника. То есть

() '

. А это оз-

начает, что окружности касаются, так как

центр гомотетии лежит на одной из них.

Обратное доказывается аналогично.

3. Решение. Пусть Н – гомотетия с цен-

тром в точке K (рис. 64) и коэффициентом

Рис. 63

=− ⇒

() () || ()H A C H AD l l AD H AD CB

⇒=⇒⇒=⇒

(')HS

окружность, вписанная

в угол

и проходящая через

точку К,

()HK K

. Таким об-

разом,

(') '' 'HS S S

⇒

''S

касаются в точке K. Прямая,

проходящая через точку K пер-

пендикулярно линии центров

Рис. 64

этих окружностей, является их общей касательной. Пусть другой

точке

на диагонали АС соответствует другая пара окружностей

''S

. Окружности

вписаны в угол

, следователь-

но, гомотетичны с центром в точке А, а значит, их касательные в

точках

параллельны. Отсюда следует, что параллельны и пер-

пендикулярные им линии центров пар окружностей

', ''SS

4. Решение. Рассмотрим случай, когда

точки

лежат по разные стороны

от прямой ВК, а точки

– по раз-

ные стороны от ВМ (рис. 65). Остальные

случаи рассматриваются аналогично.

Прямые

пересекаются в точ-

ке

, так как точки

,QP

являются об-

разами точек K и М при гомотетии с цен-

тром

, касательная переходит в

параллельную ей касательную с точкой

Рис. 65