Куцый Н.Н. Математические методы системного анализа и теория принятия решений. Пособие по курсовой работе

Подождите немного. Документ загружается.

та, который имеется на складе в ка- честве нового инструмента плюс из-

ношенный за пять дней, и количеством инструмента, используемого за пять

дней; стоимости перевозок в фиктивный пункт потребления равны нулю. Числа

в клетках (стоимости перевозок) равны стоимостям обычного или срочного ре-

монта одного инструмента или покупки одного нового инструмента. Стои-

мость

∞=

означает, как сказано выше, что инструмент, сданный в ремонт

в конце

−

го дня, не успеет вернуться к началу

−

го дня даже из срочного

ремонта (не сможет быть отремонтирован к концу

−−

)1(

дня "ни за какие

деньги"); например,

∞=

означает, что инструмент, сданный даже в срочный

ремонт в конце первого дня, еще не поступит в употребление во второй день,

так как он лишь в конце второго дня вернется из срочного ремонта. При реше-

нии транспортной задачи вместо знака ∞ следует поставить, как отмечено

выше, число М, которое гораздо больше самой высокой стоимости, которая

встречается в исходной задаче.

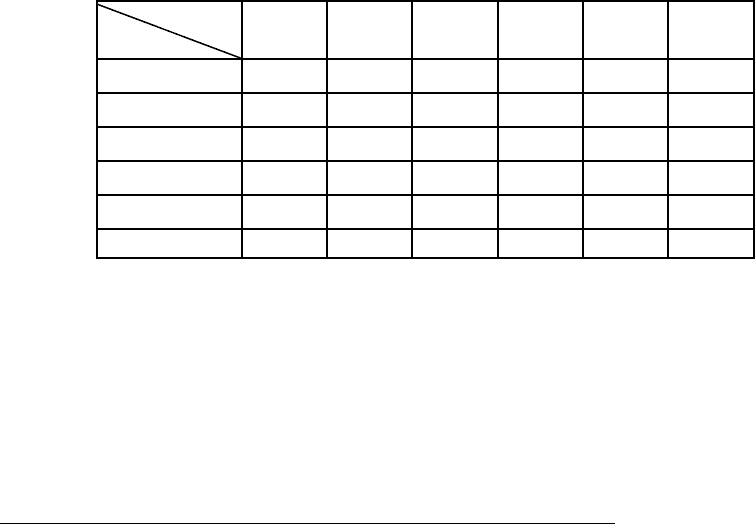
Решив эту транспортную задачу, мы получим оптимальный план, пред-

ставленный здесь в виде таблицы.

10 10 10 10 10 50

0 0

0 10 0 0

0 0 0

0 10 0

0 0 0 0

0 10

0 0 0 0 0

50 10 10 10 10 10 20

Из таблицы следует, что в первые три дня необходимо весь инструмент

покупать. В последующие два дня в употребление поступит отремонтирован-

ный инструмент, отданный в обычный ремонт в конце первого и второго дня. В

третий, четвертый и пятый дни инструмент в ремонт не сдается. Затраты на

инструмент составят

. 2001*101*106*106*106*10 рублейz

=++++=

Тема 3. Транспортная задача по критерию времени

Покажем на конкретном примере решение транспортной задачи по крите-

рию времени.

Пример. Определить оптимальный план перевозок из условия доставки

груза в кратчайший срок при следующих данных. Имеется три пункта произ-

водства однородного продукта, в каждом из которых производится количество

этого продукта:

.40 ;35 ;30

321

===

aaa

Имеется пять пунктов потребления

проводимого однородного продукта с объемом потребления в каждом из них:

.25 ;10 ;16 ;34 ;20

54321

=====

bbbbb

Задана матрица затрат времени на

перевозку однородного продукта

106143

79651

84362

где

−

время, затрачиваемое на перевозку из

−

го пункта отправления в

−

пункт потребления.

Подчеркнем два момента:

а)перевозки считаются законченными, если закончилась самая длительная

перевозка;

б)время

не зависит от количества перевозимого продукта из

−

го пунк-

та отправления в

−

й пункт потребления.

Решение. Прежде всего заметим, что если определить план перевозок из

условия минимизации функции

∑ ∑

= =

ijij

xtz

1 1

то по этому плану в общем случае продукт потребителю не будет доставлен в

кратчайший срок.

Решение задачи начинаем, как обычно, с начального опорного, построен-

ного, например, с помощью метода "северо-западного угла".

Дальнейшие расчеты можно вести одним из двух методов: 1)минимизиро-

вать функцию

но при дополнительных условиях, вводимых последовательно

в процессе решения; 2)производить последовательные преобразования реше-

ния путем построения так называемых "разгрузочных циклов".

Первый способ. 1 - ы й ш а г . Имеем начальный опорный план

2510500

0011240

0001020

Подчеркиваем в матрице

все элементы, соответствующие

плана

, и находим среди них наибольший, который обозначим

′

, т.е.

}max{

′

для всех

. Это время определяет срок, в течение которого

осуществляются перевозки, соответствующие данному решению. В рассматри-

ваемом примере

.10

′

106143

79651

84362

2 - о й ш а г . Все элементы мат- рицы, которым соответствуют

′

≥

блокируем, то есть заменяем реальные значения

на произвольно большое

число

}.max{

> >

В рассматриваемом примере блокированию подлежит

элемент, у которого

5, куда и заносим вместо

число

и тем

самым имеем матрицу

6143

79651

84362

2 - о й ш а г. Для измененной на 2-ом шаге матрицы

ищем оптимальное

решение, минимизирующее функцию

∑ ∑

= =

ijijt

xtZ

1 1

Это можно сделать, в частности, применяя метод потенциалов. В рассмат-

риваемом примере на предварительном этапе начального опорного плана

строим матрицу

′

. Представим схему, которая соответствует плану

3 3

MvB

Отсюда

00077

22000

28400

+−−

+−−−

′

Выделяем в этой матрице отрицательный элемент

+−=

′

и в матри-

це

строим замкнутый маршрут, затем производим перемещение и получаем

план

15101500

001340

1000020

Преобразуем матрицу

′

затем улучшаем план

до тех пор пока

имеется возможность. В рассматриваемом примере получим

01016410

2500010

000300

Возвращаемся к 1-ому шагу, продолжая расчеты в той же последователь-

ности

1 - й ш а г . В решении

элемент

, т.е. мы освободились от самой

длительной перевозки начального плана

. В плане

среди

находим

{ }

.max

′′

В рассматриваемом примере

′′

Поэтому на 2-ом шаге за-

писываем новую матрицу

в которой элементы

7 ,9 ,8

252415

===

ttt

заменены числом

6143

651

4362

2 - о й ша г . Исходя из этой матрицы, применением метода потенциалов

находим

0016240

5001020

2010000

И так как в этом плане элементы

соответствуют блокированным

элементам матрицы

то найденное на предыдущем этапе решение

яв-

ляется оптимальным решением, исходя из критерия времени. Этому плану со-

ответствует

часов. 7

min

Второй способ. 1 - ы й ш а г . Имеем начальный опорный план

2510500

0011240

0001020

Определяем наибольший элемент

′

из всех

соответствующих

плана

и все элементы

,tt

′

соответствующие

подчеркиваем. В

данном примере

,10

′

а элементы

для

отсутствуют.

2 - й ш а г . В плане перевозок

строим "разгрузочный" цикл, начиная с

элемента

, при этом на нечетном местах этого цикла

, при этом счита-

ем

стоящим на первом месте.

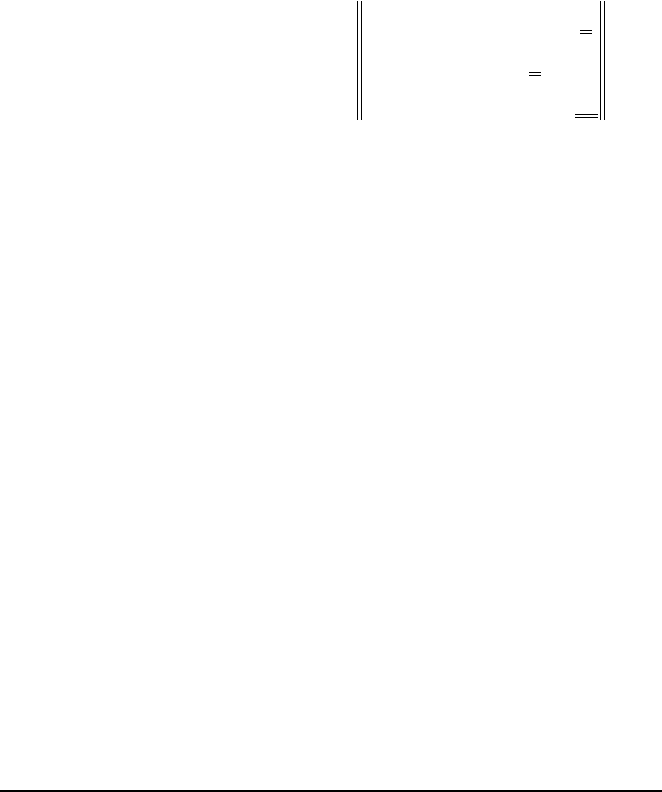
В данном случае в "разгрузоч- ный" цикл входят элементы

;10

;11

Перемещая по этому циклу число

,11}25 ,11min{

полу-

чим новый план перевозок, равный

14101600

1100240

0001020

Так как перевозка

не оказалась равной нулю, то продолжаем построе-

ние "разгрузочного" цикла, вновь начиная с элемента

Таковым будет цикл, состоящий из

;14

;11

;24

;10

;20

Перемещая по этому циклу

,14}2420, ,14min{

получим

новое решение. Как результат такого перемещения

и тем самым вновь

переходим к 1-ому этапу.

1 - ы й эта п . Наибольшим элементом

′

для элементов

плана

оказывается элемент

′

поэтому

2415

, xx

подчеркиваем.

2 - ы й эта п . На этом этапе необходимо было бы "разгрузить" элемент

. Однако построение для нее разгрузочного цикла невозможно. Действи-

тельно, если вычесть какое-либо число из элемента

, то необходимо для

сохранения баланса в 5-ом столбце матрицы

добавить такое же число к дру-

гому элементу этого столбца. Но в 5-ом столбце отсутствуют не подчеркнутые

элементы. Следовательно, "разгрузить" элемент

невозможно. На этом

основании считаем, что решение, представленное матрицей

, является иско-

мым оптимальным решением при

часов. 7

min

Тема 5. Задача оптимального назначения на авиарейсы

Авиалиния, работающая в течение всей недели, имеет расписание рейсов,

приведенное в таблице 5.1.

Поставлена следующая задача. Где должны базироваться экипажи (в пунк-

тах А и/или В) и какие рейсы они должны обслуживать, чтобы суммарное вре-

мя, которое все экипажи теряют на ожидание обратного рейса, было бы мини-

мальным, но при этом необходимо учесть, что время ожидания каждой брига-

ды должно быть больше 4 часов и меньше 24 часов.

Время 4 часа назначено исходя из того, что экипаж не должен отправлять-

ся в обратный рейс, не отдохнув в течение хотя бы четырех часов. Время 24

часа назначено исходя из того, что каждый экипаж не должен ждать рейса бо-

лее чем сутки; иначе, например, он не сможет налетать то число часов, которое

дает право на льготы при выходе на пенсию.

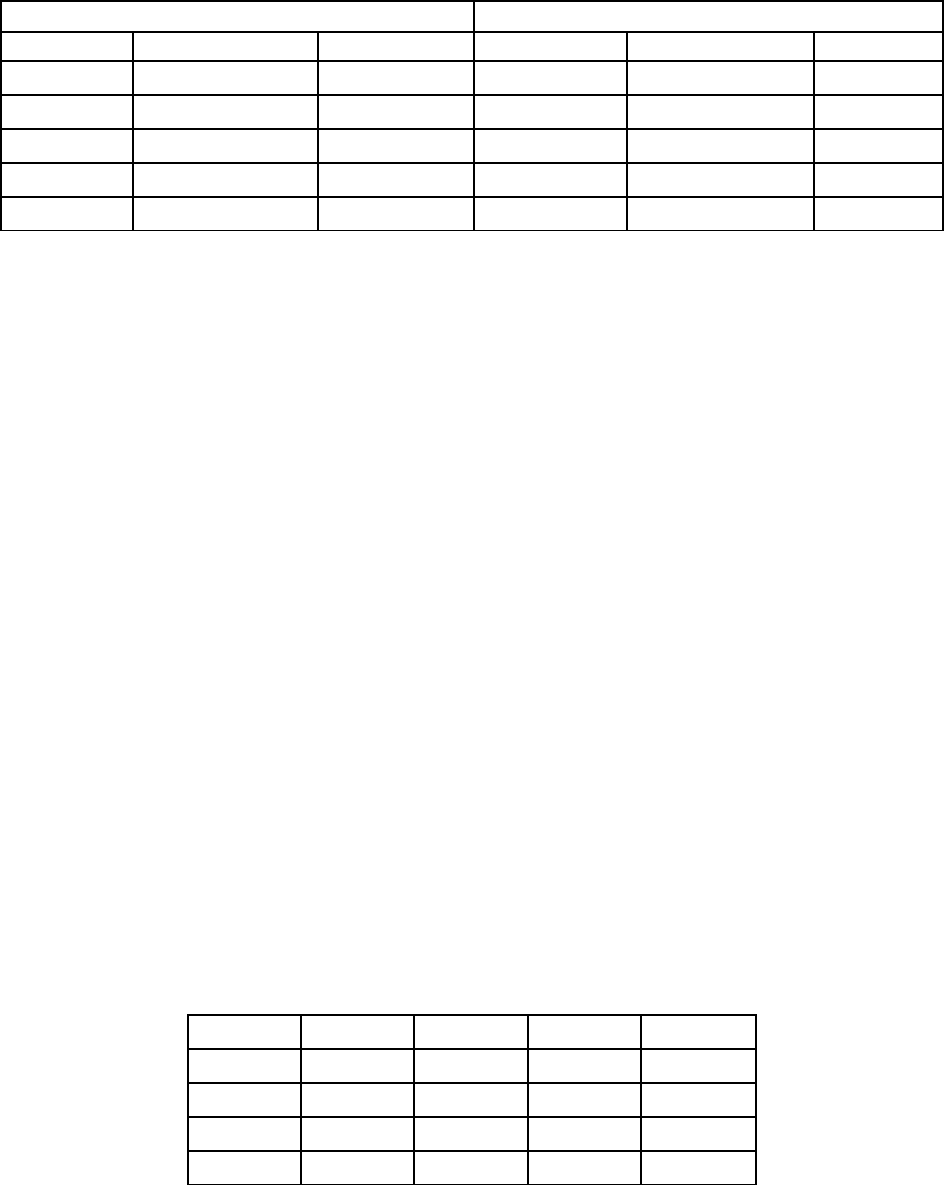
Таблица 5.1

Пункт А → пункт В Пункт В → пункт А

№ рейса Отправление Прибытие № рейса Отправление Прибытие

1 06.00 12.00 101 05.30 11.30

2 07.30 13.30 102 09.00 15.00

3 11.30 17.30 103 15.00 21.00

4 19.00 01.00 104 18.30 00.30

5 00.30 06.30 105 00.00 06.00

С целью наилучшего показа сути задачи попытаемся применить метод

перебора возможных решений, а затем убедившись, что этот метод требует

больших и практически не осуществимых затрат времени, перейдем к рассмот-

рению венгерского метода, позволяющего решить поставленную задачу.

Предположим, например, что экипаж базируется (живет) в А и обслужива-

ет рейс 3 в направлении В и рейс 102 в противоположном направлении. Этот

экипаж должен ждать в пункте В 15.5 часа (от 17.30 до 09.00). Составим путем

аналогичных расчетов две матрицы, оформленные в виде таблиц 5.2 и 5.3, эле-

менты которых отражают величины потерянного времени, считая в первом

случае, что все экипажи живут в пункте А, а во втором, что все они живут в

пункте В. В таблице 5.2. элемент

−==

)5)1(1 ;5)1(1( jit

время ожидания при об-

служивании рейса под номером

(вылет из пункта проживания А) и обслужи-

вание рейса, номер которого определяется как

100

(возвращение в пункт

проживания А из пункта В). В таблице 5.3 элемент

−==

))( ;)(( 511511 jjt

вре-

мя ожидания при обслуживании рейса под номером

100

(вылет из пункта

проживания В) и обслуживание рейса, номер которого определяется как

(воз-

вращение в пункт проживания В из пункта А).

Таблица 5.2

Все экипажи живут в пункте А

17.5 21 3 6.5 12

16 19.5 1.5 5 10.5

12 15.5 21.5 1 6.5

4.5 8 14 17.5 23

23 2.5 8.5 12 17.5

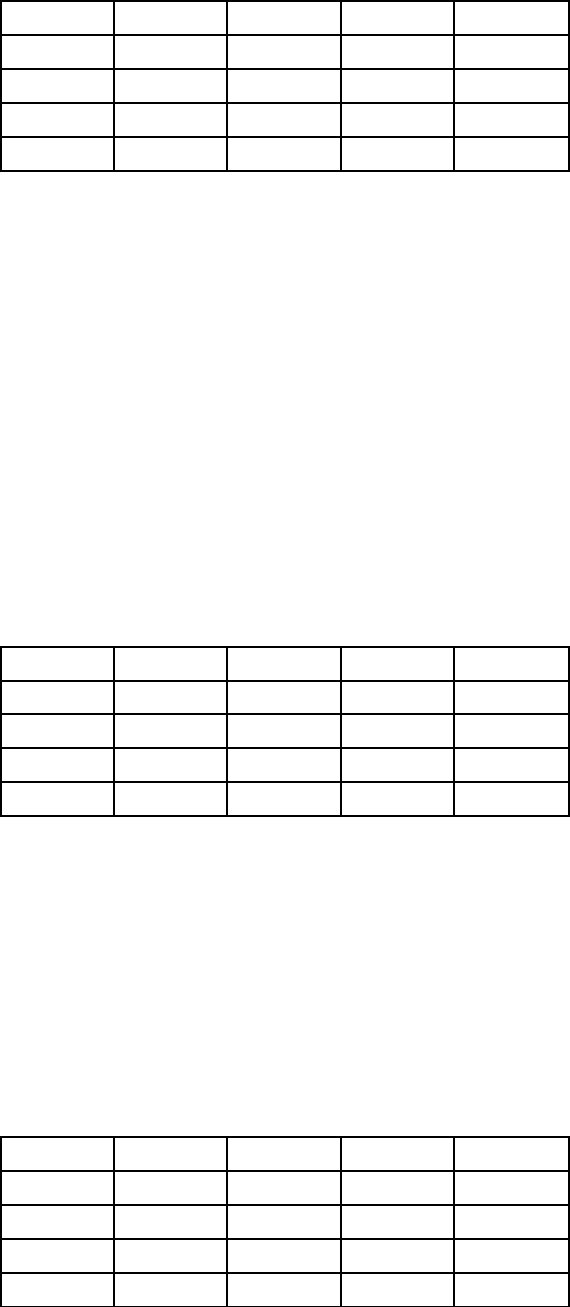
Таблица 5.3

Все экипажи живут в пункте B

18.5 15 9 5.5 0

20 16.5 10.5 7 1.5

0 20.5 14.5 11 5.5

7.5 4 22 18.5 13

13 9.5 3.5 0 18.5

Составим теперь на основе этих двух таблиц третью (таблица 5.4.), каж-

дый элемент которой будет являться меньшим из чисел, занимающих соответ-

ствующие клетки в двух исходных таблицах. При этом мы не будем принимать

во внимание числа, которые не превосходят четырех, учитывая потребности

экипажа в отдыхе. Например, если нам представится выбор между числами (1,

101; место жительства в пункте А) и (101, 1; место жительства в пункте B), то

выбрать следует (1, 101), которое дает нам ожидание в 17,5 часа вместо 18,5

часа. Напротив из (3, 102; место жительство в пункте А) и (102,3; место жи-

тельства в пункте B) мы выбираем (3, 102), хотя этому варианту и соответству-

ет меньшее время, т.к. вариант (102,3) оставляет на отдых меньше 4 часов и

поэтому неприемлем. Отметим, что время ожидания свыше 24 часов мы преду-

смотрительно не учитывали в наших таблицах.

Таблица 5.4

17,5 15 9 5,5 12

16 16,5 10,5 5 10,5

12 15.5 14.5 11 5,5

4.5 8 14 17.5 13

13 9,5 8,5 12 17,5

Назовем назначением факт приписания экипажа одному из рейсов (ска-

жем (102,1) (3,102), (104,2) и т.д.). Понятно, что каждый экипаж может быть

назначен лишь на один прямой и один обратный рейс. Тем самым, любое воз-

можное решение задачи о назначениях может быть представлено таблицей,

элементами которой являются числа 0 и 1, причем в каждой строке и в каждом

столбце имеется только одна единица, отмечающая выбранное значение. В та-

блице 5.5 приведен пример возможного решения.

Таблица 5.5

0 1 0 0 0

1 0 0 0 0

0 0 0 0 1

0 0 1 0 0

0 0 0 1 0

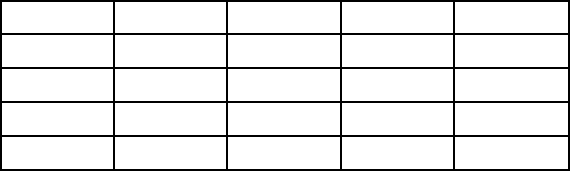
Решение, описываемое таблицей 5.5 соответствует, как можно устано-

вить рассматривая и предыдущие таблицы, рейсам (2,101), (102,1), (5,103),

(104,3), (105,4), т.е. при таком варианте трем экипажам следует базироваться в

пункте А, а двум - в пункте B. Суммарные потери времени будут составлять

15 + 16 + 5,5 + 14 + 12 = 62,5 часа.

В таблице 5.5 показано одно возможное решение, а всего для таблицы с

пятью столбцами таких решений может быть 120. Понятно, что с увеличением

размерности таблицы число вариантов заставит отказаться от метода перебора,

даже имея в распоряжении мощные ЭВМ.

Покажем, как можно решить поставленную выше задачу, применяя алго-

ритм, в основу которого положен венгерский метод. Нельзя не отметить, что в

нашем случае можно было прибегнуть и к методу перебора, решив задачу за

несколько часов, а привлекая интуицию, и быстрее. Но оставим другим метод

перебора, а сами применим венгерский метод.

Процесс решения расчленяется на шесть этапов.

ЭТАП 1. ПОЛУЧЕНИЕ НУЛЕЙ

Перед тем ознакомиться с процессом решения задачи, отметим, что нуль в

последующих таблицах будет иметь другое толкование в сравнении с толкова-

нием в таблице 5.5. Также обратим внимание, что строки последующих таблиц

будут обозначаться привычным индексом

,)1(1 ni

а столбцы -

.)1(1 nj

Сделав

эти предварительные замечания, перейдем к таблице 5.6, которая является ко-

пией таблицы 5.3.

Таблица 5.6.

17,5 15 9 5,5 12

16 16,5 10,5 5 10,5

12 15.5 14.5 11 5,5

4.5 8 14 17,5 13

13 9,5 8,5 12 17,5

Среди элементов каждого столбца этой таблицы выбираем наименьший и

вычтем его из всех элементов этого столбца. Составим таблицу, элементами

которой являются разности

),)1(1 ;)1(1( ,min

)1(

njniccc

ijijij

==−=

где для рассматриваемого случая

.5)1(1 ;5)1(1

Описанный вариант позволяет получить хотя бы один нуль в каждом

столбце. В нашем примере (таблица 5.6) нам следует вычесть 4.5 из всех эле-

ментов первого столбца, 8 из всех элементов второго столбца и т.д. Таким об-

разом мы получим числа

)1(

которые составляют следующую таблицу.

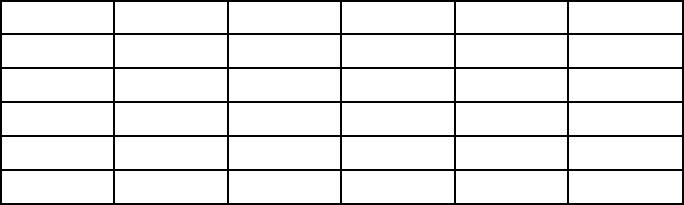
Таблица 5.7

1 2 3 4 5

1 13 7 0,5 0,5 6,5

2 11,5 8,5 2 0 5

3 7,5 7,5 6 6 0

4 0 0 5,5 12,5 7,5

5 8,5 1,5 0 7 12

ЭТАП 2. ПОИСК ОПТИМАЛЬНОГО РЕШЕНИЯ

При помощи нулевых значений

)1(

попытаемся сконструировать решение,

для которого суммарное время потерь (или в нулевых условиях других задач,

суммарные затраты) имело бы нулевое значение. Если это возможно, то мы на-

шли оптимальное решение. В противном случае мы переходим к третьему эта-

пу.

Для нахождения решения с нулевым значением, рассмотрим сначала ту

строку (или те строки), которая содержит наименьшее число нулей. Если эта

строка содержит только один нуль, то подчеркнем его двойной чертой. Если же

рассматриваемая строка содержит два и более нулей, то подчеркнем двойной

чертой один из нулей этой строки, а затем вычеркнем нули, которые находятся

в той же строке или в том же столбце, что и подчеркнутые двойной чертой

нули.

Найдем среди оставшихся строк ту (или те), которая содержит меньше

всего нулей, и повторим этот же процесс. Будем поступать так до тех пор, пока

мы уже больше не сможем подчеркивать двойной чертой новые нули.

В рассматриваемом примере вначале подчеркнут двойной чертой элемент

а затем

и после

и, наконец

и вычеркнем

хотя можно было

подчеркнуть двойной чертой

и вычеркнуть

. Тем самым получим табли-

цу 5.7а, в которой лишь первая строка и второй столбец не содержат нуля, под-

черкнутого двойной чертой, что не позволяет получить решение с итоговым

значением равным нулю. Если все же завершить назначение выбором элемента

то соответствующее значение решения

.0700007

≠=++++

Следовательно, необходим переход к следующему, третьему этапу.

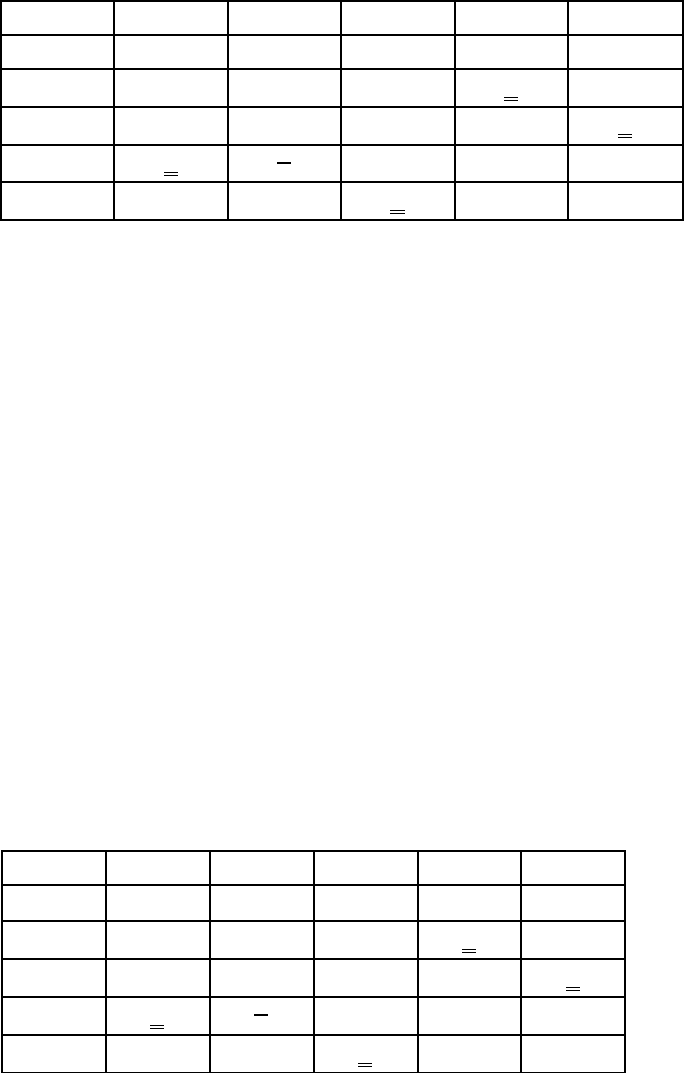
Таблица 5.7а

1 2 3 4 5

1 13 7 0,5 0,5 6,5

2 11.5 8,5 2 0 5

3 7,5 7,5 6 6 0

4 0 0 5,5 12,5 7,5

5 8,5 1,5 0 7 12

ЭТАП 3. ПОИСКИ МИНИМАЛЬНОГО НАБОРА СТРОК И СТОЛБЦОВ,

СОДЕРЖАЩИХ ВСЕ НУЛИ

Будем выполнять действия в такой последовательности:

а) пометим символом (♣) все те строки, которые не содержат ни одного

подчеркнутого двойной чертой нуля;

б) отметим каждый столбец, который содержит вычеркнутый нуль, хотя

бы в одной из помеченных строк;

в) отметим каждую строку, которая имеет подчеркнутый двойной чертой

нуль, хотя бы в одном из помеченных столбцов;

г) будем повторять поочередно (б) и (в) до тех пор, пока не останется

строк или столбцов, которые еще можно пометить.

Этот процесс позволит нам получить минимальное число строк и столб-

цов, которые содержат все подчеркнутые двойной чертой или перечеркнутые

нули. Как это происходит, будет видно на этапе 4.

В нашем примере помечена строка 1; столбцов, которые следовало бы от-

метить, нет.

Таблица 5.8

1 2 3 4 5

1 13 7 0,5 0,5 6,5

♣

2 11.5 8,5 2 0 5

3 7,5 7,5 6 6 0

4 0 0 5,5 12,5 7,5

5 8,5 1,5 0 7 12

ЭТАП 4. ЗАВЕРШЕНИЕ ЭТАПА 3

Отметим заливкой каждую н е п о м е ч е н н у ю с т р о ку и каждый п о м е -

ч е н н ый с то л б е ц . Это даст нам минимальное число строк и столбцов, кото-

рые содержат все перечеркнутые или подчеркнутые двойной чертой нули. В

рассматриваемом примере необходимо отметить заливкой строки 2,3,4,5 и не

отмечать заливкой столбцов.

Таблица 5.9