Кучер В.Я. Основы технической диагностики и теории надёжности
Подождите немного. Документ загружается.

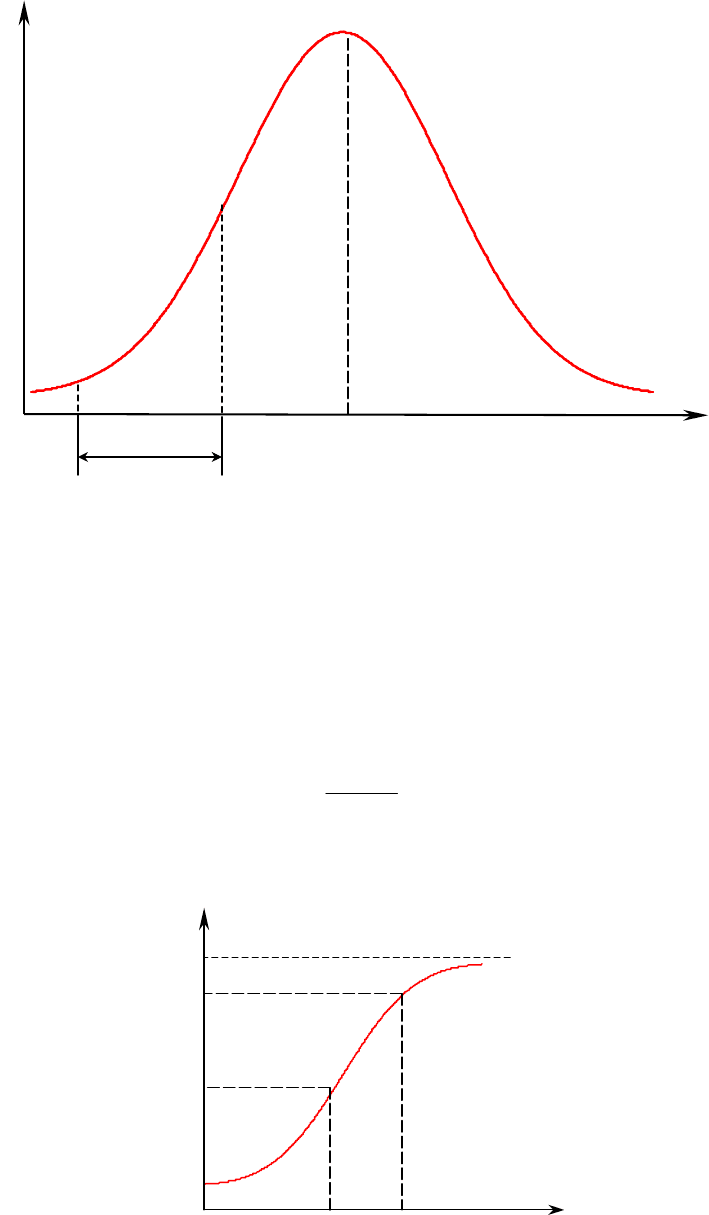
где Х – текущее значение случайной величины (переменная интегрирования в
пределах – ∞ < Х ≤ х).
f(x)
x
0 х = х
0,5
∆х
Рис. 2
П р и м е ч а н и е.
В теоретических выводах необходимо различать обоз-
начения переменного предела интегрирования и переменной интегрирования.
Интегральная функция распределения обладает следующими свойствами:
F(– ∞) = 0; F(∞) = 1. (28)
Из соотношения (27) вытекает дифференциальный закон плотности рас-
пределения непрерывной случайной величины:
)(
)(
xf
dx
xdF
= . (29)
На рис. 3 приведён график функции распределения непрерывной слу-
чайной величины.
F(x)
1
p
0,5
0 x
0,5
x
p
x
Рис. 3
11
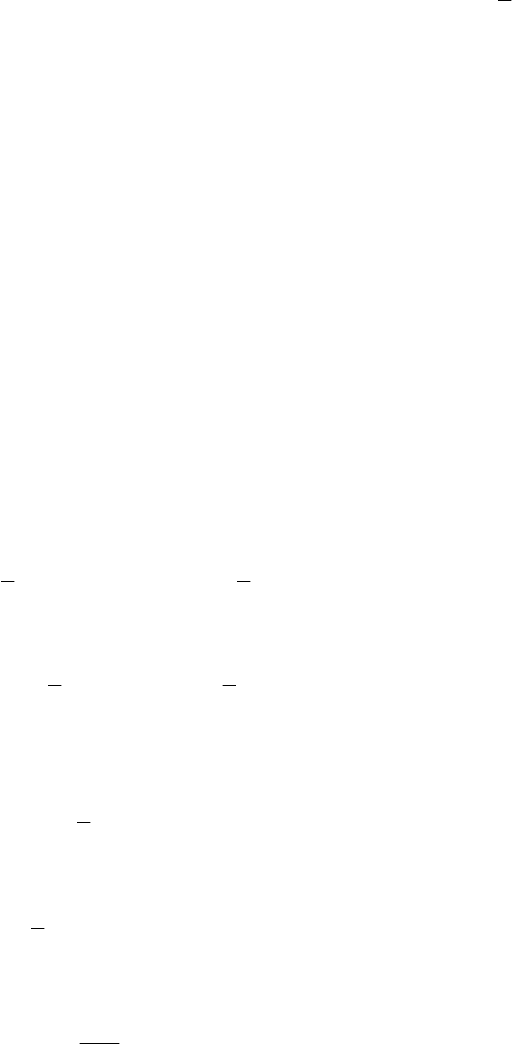
Заданной величине вероятности, например Р = 0,9, соответствует абсцисса
х
р
, так что Р(х < х
р
) = F(х
р
) = Р. Величина х
р
называется квантилем вероят-
ности Р. Например, если известны квантили х
0,1
и х
0,9
, то Р(х
0,1
≤ х ≤ х
0,9
) =
= F(x
0,9
) – F(x
0,1
) = 0,9 – 0,1 = 0,8. Квантиль, соответствующий вероятности
Р = 0,5, называется медианой распределения. Медиана распределения х = х
0,5
делит кривую плотности распределения на две равные части
∫∫
∞−
∞
==
0,5
5,0
x
x
0,5)()( dxxfdxxf .
Для математического ожидания и среднеквадратичного отклонения непре-
рывных и дискретных случайных величин справедливы следующие свойства.
Математическое ожидание постоянной величины с равно ей самой
с = с.
Постоянный множитель может быть вынесен из-под знака математическо-
го ожидания М [cx] = сM [x].
Cреднеквадратичное отклонение постоянной величины σ [c] = 0.
Среднеквадратичное отклонение при линейном преобразовании случай-
ной величины σ [cx + a] = |c| σ [x], т.е. прибавление постоянной величины к
случайной не изменяет среднеквадратичного отклонения.
Важную роль в теории вероятности играют моментные характеристики
распределений. Различают начальные и центральные моменты распределе-
ния, которые определяются порядком k.
Начальный момент порядка k для непрерывных распределений
, (30)
∫
+∞
∞−
== ][)(
kk
k
xMdxxfxm
для дискретных распределений
. (31) ][
k
i
k
i
r
1i
k
xMРxm ==
∑
=
Центральный момент порядка k для непрерывных распределений
∫
∞
∞−
−=−= ])[()()(
kk
k
xxMdxxfxxM , (32)
для дискретных распределений
])[()(
k
i
k
r
1i
ik
xxMPxxM −=−=
∑
=
. (33)
Центральный момент нулевого порядка М
0
= 1.
Центральный момент первого порядка
∫
∞
∞−
=−= 0)()(
1
dxxfxxM . (34)
Центральный момент второго порядка (дисперсия)
22
2
)()( σ==−=
∫
∞
∞−
DdxxfхxM . (35)
Центральный момент третьего порядка (асимметрия)
3
3
σ
=
М
А . (36)
12
Центральный момент четвёртого порядка (эксцесс)
Е
М
=−
σ
3
4
4
. (37)
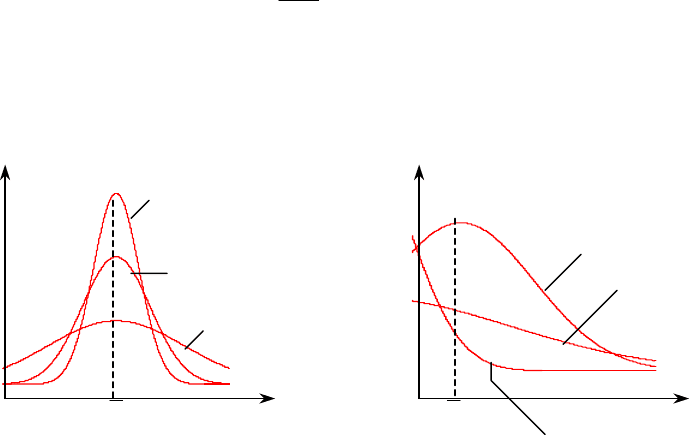
На рис. 4 и 5 приведены графики центральных моментов третьего и чет-
вёртого порядка с различной асимметрией и эксцессом.
f(x) f(x)
E > 0
А = 0
E = 0 А > 0
E < 0
0
х
х 0
х
х
А < 0
Рис. 4 Рис.5
Эксцесс характеризует «острую» (Е > 0) или «сглаженную» (Е < 0) верши-
ну распределения по сравнению с некоторым эталонным распределением
(Е = 0), в качестве которого принимается нормальное распределение. Асим-
метрия характеризует форму кривой распределения.
13
2. ОСНОВЫ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ
2.1.Основные положения
Состояние объекта описывается совокупностью (множеством) определя-
ющих его параметров (признаков). Распознавание состояния объекта – отне-
сение состояния объекта к одному из возможных классов (диагнозов). Число
диагнозов (классов, типичных состояний, эталонов) зависит от особенностей
задачи и целей исследований [3], [4].
Часто требуется провести выбор одного из двух диагнозов (дифференци-
альная диагностика или дихотомия);
например, «исправное состояние» или
«неисправное состояние». В других случаях необходимо более подробно
охарактеризовать неисправное состояние. В большинстве задач технической
диагностики диагнозы (классы) устанавливаются заранее, и в этих условиях
задачу распознавания часто называют задачей классификации.
Совокупность последовательных действий в процессе распознавания
называется алгоритмом распознавания. Существенной частью процесса
распознавания является выбор параметров
, состояния объекта. Они должны
быть достаточно информативны, чтобы при выбранном числе диагнозов
процесс разделения (распознавания) мог быть осуществлён.
В задачах диагностики состояние объекта часто описывается с помощью
комплекса признаков
K = (k
1
, k
2
, … , k
j
, … , k
ν
), (38)
где k
j
– признак, имеющий m
j
разрядов.
Пусть, например, признак k
j
представляет собой трёхразрядный признак
(m
j
= 3), характеризующий температуру газа за турбиной: пониженная, нор-
мальная, повышенная. Каждый разряд (интервал) признака k
j
обозначается
k
js
, например, повышенная температура за турбиной k
j3
. Фактически наблюда-
емое состояние соответствует определённой реализации признака, что отме-
чается верхним индексом
*
. Например, при повышенной температуре реали-
зация признака k
j
*
= k
j3
.
Объект соответствует некоторой реализации комплекса признаков
K
*
= (k
1
*
, k
2
*
, … , k
j
*
, … , k
ν
*
). (39)
Во многих алгоритмах распознавания объект удобно характеризовать
параметрами х
j
, образующими ν-мерный вектор или точку в ν-мерном
пространстве.
Х = (х
1
, х
2
, … , х
j
, … , х
ν
). (40)
С помощью признака k
j
получается дискретное описание, тогда как параметр
х
j
даёт непрерывное описание. Принципиальных отличий при описании
объекта с помощью признаков или параметров нет, поэтому используют оба
вида описания.
Существуют два основных подхода к задаче распознавания: вероятност-
ный и детерминистский.
14
Постановка задачи при вероятностных методах распознавания такова.
Имеется объект, который находится в одном из п случайных состояний D
i
.
Известна совокупность признаков (параметров), каждый из которых с опре-
делённой вероятностью характеризует состояние объекта. Требуется постро-
ить решающее правило, с помощью которого предъявленная (диагностируе-
мая) совокупность признаков была бы отнесена к одному из возможных
состояний (диагнозов). Желательно также оценить достоверность принятого
решения и степень риска ошибочного решения.
При детерминистских методах
распознавания удобно формулировать
задачу на геометрическом языке. Если объект характеризуется ν-мерным
вектором, то любое состояние объекта представляет собой точку в ν-мерном
пространстве параметров (признаков). Предполагается, что диагноз D
i
соот-
ветствует некоторой области рассматриваемого пространства признаков. Тре-
буется найти решающее правило, в соответствии с которым предъявленный
вектор
Х
*
(диагностируемый объект) будет отнесён к определённой области
диагноза. Таким образом, задача сводится к разделению пространства
признаков на области диагнозов. При детерминистском подходе области
диагнозов обычно считаются «непересекающимися», т.е. вероятность одного
диагноза (в область которого попадает точка) равна единице, вероятность
других равна нулю. Подобным образом предполагается, что и каждый
признак
либо встречается при данном диагнозе, либо отсутствует.
Вероятностный и детерминистский подходы не имеют принципиальных
различий. Более общими являются вероятностные методы, но они требуют
значительно большего объёма предварительной информации.
2.2. Статистические методы распознавания
Среди методов технической диагностики широкое распространение нашли
метод, основанный на обобщённой формуле Байеса, и метод последователь-
ного анализа, предложенный Вальдом [1].
Обобщённую формулу Байеса рассмотрим на следующем примере. Пусть
событие А связано с одним из событий В
1
, В
2
, … , В
n
, образующих полную
группу несовместных событий. Для определённости будем считать, что А –
появление признака (например, появление стружки в масле), а В
1
, В
2
, … , В
n
–
неисправность соответствующих узлов электрической машины. Принимает-
ся, что при этом признаке один из узлов машины является неисправным, а
одновременный отказ двух узлов маловероятен и исключается из рассмотре-
ния. На основании статистической информации об отказах при испытаниях и
эксплуатации известна вероятность отказа отдельных узлов: Р(В
1
), Р(В
2
), … ,
Р(В
n
). Задача сформулирована таким образом: произошло событие А (появле-
ние стружки). Какова вероятность, что причиной появления стружки являет-
ся неисправность узла В
i
?
Предполагается, что частота встречаемости (вероятности) признака А при
неисправностях отдельных узлов Р(А/В
i
) рассчитана на основании статисти-
15

ческой информации об отказах. Вероятность одновременного появления
признака А и состояния В
i
Р(А В∧
i
) = Р(А) Р(B
i
/А) = Р(B
i
) Р(А/В
i
). (41)
Из этого равенства находим вероятность состояния B
i
(неисправность узла
B
i
):
Р(B
i
/А) = Р(B
i
) Р(А/В
i
). (42)
Искомая вероятность найдена, но остаётся выяснить величину Р(А) – веро-
ятность появления признака А. Так как признак появляется вместе с неис-
правностью какого-либо узла, то это событие представляет собой логическую
сумму отдельных событий
А = (А
В∧
1
) (А∨
∧
В
2
) … (А∨ ∨
∧
В
n
). (43)
В соответствии со сделанным предположением должно реализоваться
только одно из возможных событий, и потому Р(А) = Р(А
В∧
1
) + Р(А
∧
В
2
) + …
… + Р(А
В∧
n
) или
. (44)
∑
=
=
n
1j
jj
)/()()( BAPBPAP
Равенство (44) называют формулой полной вероятности события А,
происходящего вместе с полной группой независимых событий. Она выража-
ет следующий принцип: если объект имеет несколько возможных несовмес-
тных путей перехода в другое состояние, то вероятность перехода равна
сумме вероятностей осуществления каждого из них.
Несовместные пути –
это пути, которые не могут реализоваться одновременно.
Из соотношений (42) и (44) вытекает формула Байеса
)/()(
)/()(
)/(
jj
n
1j
ii
1
BAPBP
BAPBP
ABP
∑
=
=
. (45)
Вероятность состояния
после появления признака А, т.е. величину
, называют апостериорной [в отличие от априорной вероятности
].
i
B
)/(
i
ABP
)(
i
BP
П р и м е ч а н и е.
Термины «априори» и «апостериори» означают «до
опыта» и «после опыта», т.е. представляют наличие или отсутствие признака
А.
Из равенства (45) следует
= 1. (46)
)(
i
n
1i
/ABP
∑
=
Из формулы Байеса получается, что для двух состояний отношение апос-
териорных вероятностей
)/()(
)/()(
)/(
)/(
ll
kk
l
k
BAPBP
BAPBP
АBP
АBP
= . (47)
Если при состоянии B
k
признак А встречается чаще, чем при состоянии B
l
,
т.е. Р(А/В
k
) > Р(А/В
l
), то вероятность этого состояния после получения
информации о появлении признака А увеличивается.
16

Пример 2.1. Известно, что 90% шарикоподшипников электрических
машин вырабатывает ресурс в исправном состоянии. Признак А – повышение
температуры масла выше нормальной на 30º С – встречается у исправных
подшипников только в 5% случаев. Требуется определить вероятность
исправного состояния подшипника при появлении признака А.
Решение:
Назовём исправное состояние В
1
, неисправное В
2
.
Известно, что Р(В
1
) = 0,05; Р(В
2
) = 0,95.
По формуле (45)
.32,0
95,01,005,09,0
05,09,0
)()()()(
)()(
)(
2211
11
1
=
⋅+⋅
⋅
=
+
=
A/BPBPA/BPBP
A/BPBP
/ABP
Вероятность исправного состояния подшипника понизилась с 0,9 до 0,32.
Метод последовательного анализа, предложенный Вальдом, применяется
для дифференциальной диагностики (распознавания двух состояний),
контроля качества выпускаемой продукции [7] и планирования контрольных
испытаний на надёжность. В отличие от метода Байеса для распознавания
состояний D
1
и D
2
составляется отношение (для независимых признаков)
)()(
)()(
)(
)(
)(
)(
1н11
2н21
1
2
1
2
/DkP/DkP
/DkP/DkP
DP
DP
/KDP
/KDP
**
**
*
*
…
…
⋅= , (48)
если
)(
)(
1
2
*
*
/KDP
/KDP
> 1 (49)
или
)()(
)()(
1н11
2н21
/DkP/DkP
/DkP/DkP
**
**
…
…
>
)(
)(
2
1
DP
DP
, (50)
то принимается решение K
*
∈
D
2
.
В методе последовательного анализа рассматриваемые отношения вероят-
ностей признаков (отношения правдоподобия) составляются не сразу, а в
последовательном порядке; поэтому требуется меньшее число обследований
(объём испытаний).
Пример 2.2. При диагнозе D
1
простой признак k
1
встречается с вероят-
ностью
P(k
1
/D
1
) и отсутствует с вероятностью Р(
1
k /D
1
), для диагноза D
2
соот-
ветственно
P(k
1
/D
2
) и Р(
1
k /D
2
). Если у объекта K
*
наблюдается признак k
1
и
при диагнозе
D
2
он встречается значительно чаще, чем при D
1
, то можно
сделать вывод в пользу
D
2
при
)(
)(
11
21
/DkP
/DkP
> А K
*
∈
D , (51)
2
где
А – верхняя граница принятия решения.
В противоположном случае, когда признак
k
1
значительно чаще встреча-
ется при диагнозе
D
1
, принимается решение в пользу D
1
при
17

)(
)(
11
21
/DkP
/DkP
< В K
*
∈
D
1
, (52)
где
В – нижняя граница принятия.
Если отношение вероятностей (отношение правдоподобия)
В <
)(
)(
11
21
/DkP
/DkP
< А, (53)
то для решения требуется дополнительная информация, тогда проводятся
испытания по признаку
k
2
, и пусть у диагностируемого объекта этот признак
отсутствует.
Составляется произведение двух отношений правдоподобия и при
)(
)(
11
21
/DkP
/DkP
·
)(
)(
12
22
/DkP
/DkP
> А K
*
∈
D (54)
принимается решение об отнесении объекта к диагнозу
D . Подобным
образом учитывается нижняя граница принятия решения. Если признаки
зависимые, то используется отношение
2
2
)
2
D(
12
/kkP / )(
112
D/kkP , в котором
учитывается вероятность отсутствия признака
2
k , при условии, что признак
k
имеется. Дополнительные испытания проводятся до тех пор, пока при выб-
ранных границах А и В можно принять определённое решение.
1
Иногда рассматривают не отношение правдоподобия, а натуральный лога-
рифм этого отношения, тогда условие (54) принимает вид
ln[P(k
1
/D
2
)/P(k
1
/D
1
)] + ln[P(
2
k /D
2
)/P(
2
k /D
1
)] > lnA.
Подобная форма применяется при нормальном распределении количест-
венных признаков.
Общая процедура метода такова. Считаем, что признаки являются неза-
висимыми и проведено ν – 1 испытаний, которые ещё не дали возможности
принятия решения,
В <
)()(
)()(
1r11
2r21
/DkP/DkP
/DkP/DkP
**
**
…
…
< А; r = 1, 2, … , ν – 1, (55)
но после ν-го испытания
)()(
)()(
1н11
2н21
/DkP/DkP
/DkP/DkP
**
**
…
…
> А. (56)
Тогда принимается решение об отнесении объекта к диагнозу D
2
, т.е.
K
*
∈
D . Если после ν-го испытания
2
)()(
)()(
1н11
2н21
/DkP/DkP
/DkP/DkP
**
**
…
…
< В, (57)
то объект относится к диагнозу D
1
. Для сокращения стоимости и объёма
испытаний на надёжность их планирование следует проводить с учётом
наиболее информативных признаков [8].
18

Этот метод пригоден и для непрерывно распределённых диагностических
параметров, х
1
и х
2
, но вместо вероятностей признаков в неравенства (55)-(57)
входят плотности вероятностей параметров.
При распознавании могут быть ошибки двоякого рода. Ошибка, относяща-
яся к диагнозу D
1
(принимается решение о наличии диагноза D
2
, когда в
действительности объект принадлежит диагнозу D
1
), называется ошибкой
первого рода α. Ошибка, относящаяся к диагнозу D
2
(принимается решение в
пользу диагноза D
1
, когда справедлив диагноз D
2
), называется ошибкой
второго рода β.
Допускаем выполнение неравенств (55) и (56) и принимаем решение в
пользу диагноза D
2
; тогда вероятность того, что это решение будет
справедливым, равна 1 – β. Вероятность принадлежности объекта с другой
реализацией признаков к диагнозу D
1
составляет α. С другой стороны, в силу
неравенства (56), вероятность диагноза D
2
, по крайней мере, в А раз больше,
чем диагноза D
1
, т.е.
А≥
−
α
β
1
. (58)
Подобным образом можно получить и следующую оценку:
α
β
−
≥
1
В . (59)
П р и м е ч а н и е. При планировании и нормировании испытаний на
надёжность обычно принимают α = β = 0,05 ÷ 0,20. При этом, чем меньше
значения ошибок α и β, тем больше объём и дороже испытания.
2.3. Элементы теории информации
В технической диагностике, особенно при построении оптимальных диаг-
ностических процессов, широко используется теория информации [9], [10],
как общая теория связи статистических систем. В диагностике такими систе-
мами являются система состояний (диагнозов) и связанная с ней система
признаков. Центральное место в теории информации занимает понятие
энтропии системы.
Величина Н(А) называется энтропией (
степенью неопределённости) сис-
темы А, имеющей n возможных состояний с вероятностями Р(А
1
), Р(А), …
…, Р(А
n
)
∑∑
==
−==
n
1i
ii
n
1i
i
i
)(log)(
)(
1
log)()( APAP
AP
APAH . (60)
Энтропию системы часто вычисляют с помощью двоичных логарифмов
Н(А)
. (61)
∑
=
−=
n
1i
i2i
)(log)( APAP
П р и м е ч а н и е. В формуле (60) логарифм может быть взят по любому
основанию – изменение основания приводит только к появлению множителя,
т.е. к изменению единицы измерения.
19

При выборе двоичных логарифмов в качестве единицы энтропии прини-
мается степень неопределённости системы, имеющей два возможных, равно-
вероятных состояния. Эта единица измерения называется двоичной единицей
или битом. Название бит происходит от английских слов binary digit –
двоичная единица (две начальные и конечная буквы).
Если принять при вычислении энтропии десятичные логарифмы, то в
качестве
единицы использовалась бы неопределённость системы, имеющей
10 равновероятных состояний (десятичная единица).
Пример 2.3. Вычислить энтропию системы, имеющей два равновероят-
ных состояния Р(А
1
) = Р(А
2
) = 0,5.
Решение:
Н(А) = – Р(А
1
)log
2
P(A
1
) – P(A
2
)log
2
P(A
2
) = – 0,5 log
2
0,5 – 0,5 log
2
0,5 = 1.
Часто при определении количества информации относительно системы А
получают с помощью наблюдения за другой, связанной с ней системой В.
Обычно эта вторая система (система сигналов) даёт информацию о состоя-
нии основной системы. Среднюю величину этой информации, или информа-
тивность системы В относительно системы А, можно определить из
равенства
J
A
(B) = H(A) – H(A/B). (62)
В правой части уравнения (62) содержится разность первоначальной
энтропии системы А и её энтропии после того, как стало известным состоя-
ние системы сигналов В. Так как системы А и В являются связанными, то, в
свою очередь, знание состояния системы А изменит априорную вероятность
состояний
системы В. Например, если известно, что объект находится в
неисправном состоянии, то вероятность поступления тех или иных сигналов
также изменится.
Средняя информация, содержащаяся в системе А относительно системы В
J
B
(A) = H(B) – H(B/A), (63)
тогда J
A
(B) = J
B
(A) (64)
выражает свойство взаимности информации, так как Н(А/В) = Н(АВ) – Н(В),
то J
A
(B) = H(A) + H(B) – H(AB) (65)
или
(66)
.)()lo(
)()lo()()lo()(
m
1j
ji2ji
n
1i
n
1j
j2j
n
1i
i2iA
∑∑
∑∑
==
==
+
+−−=
BAPgBAP
BPgBPAPgAPBJ
Если учесть, что
и , то
∑
=
=
m
1j
jii
)()( BAPAP
∑
=
=
n
1i
jii
)()( BAPBP
∑∑∑∑∑∑
======
+−−=
n
1i
m
1j
ji2ji
n
1i
m
1j
i2ji
n
1i
m
1j
i2jiA
)()lo()()lo()()lo()( BAPgBAPBPgBAPAPgBAPBJ
и в окончательном виде получаем симметричную формулу для информации,
которую несёт система сигналов В относительно состояния системы А
∑∑
==
=
n
1i
m
1j
ji
ji
2jiA
)()(
)(
)lo()(
BPAP
BAP
gBAPBJ . (67)
20
