Крючкова Е.Н. Основы математической логики и теории алгоритмов

Подождите немного. Документ загружается.

g n

↘ ↘

o o

↙ ↙

p p

↙

o p t

↘

↙

Построенные деревья представляют только последовательные пары символов.

Чтобы построить деревья, соответствующие цепочкам, надо сформировать для каж-

дого символа новое дерево путей, последовательно присоединяя к вершинам с пусты-

ми правыми связями имеющиеся деревья парных символов. Например, для символа

n получится дерево

↘

↙ ↘

p p

↙ ↙

t t

Постройте самостоятельно дерево для символа e, чтобы убедиться в необходимо-

сти рекурсивного присоединения поддеревьев к дереву путей в процессе его постро-

ения. Как алгоритм формирования дерева, так и алгоритм вывода всех слов при

обходе дерева путей являются рекурсивными.

При таком присоединении теряется информация о наличии последовательного

пути в матрице, т.к. одна вершина дерева пар может соответствовать одной и той

же букве, расположенной в разных частях матрицы. Чтобы восстановить эту ин-

формацию в дереве путей, каждой вершине этого дерева необходимо поставить в

соответствие набор индексов матрицы, и либо на этапе формирования дерева путей,

либо на этапе его обхода учесть правило преобразования списка индексов текущей

вершины в список допустимых индексов ее правого потомка. Ниже приведена про-

грамма формирования дерева путей, в которой не выполняется соответствующий

контроль. Дополнить программу контролем на допустимые индексы предлагается в

качестве упражнения. При формировании такого списка необходимо учесть времен-

ную и емкостную сложность контроля.

// цепочки из букв на квадрате N*N

#include <stdio.h>

#include <STDLIB.H>

#define MAXK 20 // размер матрицы

#define MaxBukva 26 // число букв в алфавите

#define index(s) (int)(s)-(int)(’a’)

141

struct TTree {

char b; // индекс буквы

int left, right; // индексы поддеревьев

};

int uk[MaxBukva]; // указатель на деревья для букв

TTree a [MaxBukva*(MaxBukva-1)/2];

// двухуровневые деревья для букв из матрицы

int first; // указатель на первый свободный элемент в дереве "a"

TTree b [MaxBukva*(MaxBukva-1)*MAXK/2]; // результирующие деревья

int first_b; // указатель на первый свободный элемент в дереве "b"

char matr[MAXK+3][MAXK+3]; // матрица из слов - по краям нули

int n; // фактический размер матрицы

FILE *in = fopen("input.txt","r");

FILE *out= fopen("output.txt","w");

void GetData(void)

{

fscanf(in,"%d\n",&n);

int i,j; char s;

for(i=0; i<MAXK*MAXK; i++) {a[i].left=-1; a[i].right=-1;}

for(i=0; i<MaxBukva; i++) uk[i]=-1;

for(i=0; i<n+2; i++) for(j=0; j<n+2; j++) matr[i][j]=’\1’;

for(i=0; i<MaxBukva; i++)

{

a[i].b=’\0’; a[i].left =-1; a[i].right=-1; //нет потомков

}

first=0;

for(i=0; i<n; i++)

{

for(j=0; j<n; j++)

{

fscanf(in,"%c",&s); matr[i+1][j+1]=s;

}

while ((s!=’\n’) && (!feof(in)) ) fscanf(in,"%c",&s);

}

void SetNewRight(int t, int next)

{

if (uk[t]==-1)

{ // пока еще нет потомков справа

uk[t]=first;

a[first].b=next; a[first].left =-1; a[first].right=-1;

first++;

return;

}

142

if ( a[uk[t]].b == next ) return; // равные не вставляем

if ( a[uk[t]].b > next )

{ // надо вставить первым в списке потомков

a[first].b=next; a[first].right=-1; a[first].left=uk[t];

uk[t]=first;

first++;

return;

}

// ищем место вставки:

int tek=uk[t];

while ( (a[a[tek].left].b < next) && (a[tek].left!=-1) )

tek=a[tek].left;

if (next==a[ a[tek].left].b) return; //равные игнорируем

// вставляем после tek:

a[first].b=next; a[first].right=-1;

a[first].left=a[tek].left; a[tek].left=first;

first++;

return;

}

void Construct(void)

// построить один уровень потомков по соседям matr

{

int i, j, k;

// приращения индексов для соседа:

int di[]= { 0, 0, 1, -1, 1, 1, -1, -1 },

dj[]= { 1, -1, 0, 0, -1, 1, -1, 1 };

for(i=1; i<n+1; i++)

for(j=1; j<n+1; j++)

for(k=0; k<8; k++)

if( matr[i][j] < matr[i+di[k]][j+dj[k]] )

SetNewRight(index(matr[i][j]),

index(matr[i+di[k]][j+dj[k]]) );

}

void PrintTree(int t, // вершина дерева

int i, // текущая длина

int len, // какой длины слова нужно печатать

char *res ) // формируемое слово

{

if (t==-1) return; // нет потомков

int tek=t;

do {

res[i]=(char)(b[tek].b+’a’); res[i+1]=’\0’;

if (i+1==len) fprintf(out,"%s\n",res);

if((i+1<len) && (b[tek].right!=-1))

PrintTree(b[tek].right, i+1, len, res);

tek=b[tek].left;

} while (tek!=-1);

}

143

void CopyTree(int t)

// приписать копию дерева из "a" к листу t дерева "b"

{

if (uk[b[t].b]==-1) return;

b[t].right=first_b; // копируется исходная цепь в конец b

int l=uk[b[t].b], i,j;

for ( j=first_b; l!=-1; j++)

{

b[j].b=a[l].b;

b[j].right=-1;

if (a[l].left!=-1) b[j].left=first_b+1;

else b[j].left=-1;

l = a[l].left;

first_b++;

}

void Form(int t)

// доформирование дерева в соответствии с его высотой

// t - вершина в массиве b, от которой идет доформирование

{

int tek=t;

while(tek!=-1)

{

if ( (b[tek].right==-1)&& (uk[b[tek].b]!=-1) )

{ CopyTree(tek); Form(b[tek].right); }

else if (b[tek].right!=-1) Form(b[tek].right);

tek=b[tek].left;

}

int main(void)

{

int i,j,len; char res[MaxBukva+2];

GetData();

Construct();

for (i=0; i<first; i++)

{

b[i].left=a[i].left;

b[i].right=a[i].right;

b[i].b=a[i].b;

}

first_b=first; // получили копию двухуровневого дерева в "b"

for(j=0; j<MaxBukva; j++)

Form(uk[j]); // достроили дерево вглубь

for (len=3; len<=MaxBukva; len++)

for (i=0; i<MaxBukva; i++)

{

144

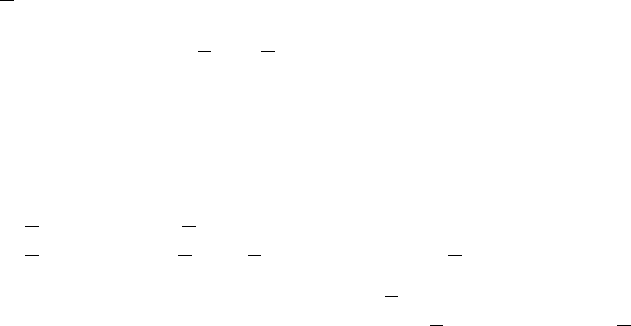
res[0]=(char)(’a’+i); res[1]=’\0’;

PrintTree(uk[i], 1, len, res);

}

fclose(in); fclose(out);

return 0;

}

6.2 Устранение рекурсии

Как правило, разработка рекурсивного алгоритма в тех случаях, когда это име-

ет смысл, существенно ускоряет процесс программирования и приводит к простой и

ясной структуре программы. К сожалению, большая глубина рекурсивных вызовов

может привести к невозможности работы программы. В таких случаях возникает за-

дача преобразования рекурсивной программы в нерекурсивную. Однако, известно,

что не существует общего алгоритма преобразования произвольного рекурсивного

алгоритма в нерекурсивный без использования моделирования рекурсивных вызовов

с помощью стека. Известно лишь, что это можно просто сделать для примитивно–

рекурсивных схем и достаточно просто для схем, сводящихся к примитивной рекур-

сии.

Рассмотрим сначала схему возвратной рекурсии. Пусть g

(x), . . . , g

(x) — всюду

определенные функции, удовлетворяющие для всех значений x условиям

(x) < x (i = 1, . . . , k).

Функция f(x, y) получается возвратной рекурсией из функций

w(x), h(x, y, z

, . . . , z

)

и вспомогательных функций

(x), . . . , g

(x), ∀

∀

(x) < x,

если

f(x, 0) = w(x)

f(x, y + 1) = h(x, y, f(x, g

(y + 1)), . . . , f (x, g

(y + 1)).

Иными словами, значение функции f в точке ⟨x, y + 1⟩ вычисляется рекурсивно

через значения этой функции в k предыдущих точках ⟨x, g

(y + 1)⟩, . . . , ⟨x, g

(y + 1)⟩,

не обязательно отстоящих от этой текущей точки на единицу.

Возвратная рекурсия теоретически сводится к примитивной, однако, в общем слу-

чае реализация соответствующей нерекурсивной программы вызывает затруднения.

В частных случаях, особенно при k = 1, перевод рекурсии в итерацию осуществля-

ется просто. Достаточно определить значение в начальной точке, а затем увеличить

аргумент y по обратному закону

−1

(y).

Рассмотрим, например, алгоритм возведения числа в натуральную степень:

= 1,

= (a

)

2n+1

= (a

)

∗ a.

Этой схеме соответствует программа:

145

long int deg(long int a,int n)

{

long int x;

if (n==0) return 1;

x=deg(a,n/2);

if (n%2==0) return x*x;

else return x*x*a;

}

Очевидно, что на каждом уровне этой рекурсивной схемы анализируется соответ-

ствующий разряд в двоичном представлении показателя степени. Причем в рекур-

сивном алгоритме анализ выполняется начиная с младшего разряда, но выполнение

умножений возможно только после выполнения вычислений на предыдущем уровне.

Спуск продолжается до тех пор, пока не будет достигнут старший разряд числа.

Тогда нерекурсивная программа имеет вид:

#define FirstSign 0x1000

// старшая анализаруемая единица степени

long int deg(long int a,int n)

{

long int x;

if (n==0) return 1;

// вычислим положение единицы в FirstSign

int i=FirstSign;

while ( (i & n) ==0x0) {i=i>>1;} // узнали номер старшей позициив степени

i=i>>1; x=a;

while (i) // не закончилась степень n

{

if ( (n & i) == 0x0) x=x*x;

else x=x*x*a;

i=i>>1;

}

return x;

}

В общем случае к каждому алгоритму надо подходить индивидуально, моделируя

те действия, которые выполняет рекурсивная программа, полученная в результате

трансляции. Это означает, что в нерекурсивном эквиваленте рекурсивного алгоритма

необходимо описать магазин, каждый элемент которого содержит:

1) данные, являющиеся исходной информацией для рекурсивной процедуры;

2) внутренние (локальные ) данные рекурсивной процедуры, если они есть.

Каждое обращение к рекурсивной процедуре в нерекурсивной программе соответ-

ствует занесению информации в магазин. Каждый выход из рекурсии соответствует

стиранию информации из магазина. Общая структура нерекурсивной программы

соответствует циклу типа "while который выполняетмя при условии, что магазин не

пуст.

Рекурсивный алгоритм всегда реализуется с помощью вызывающей программы, в

которой происходит обращение к рекурсивной процедуре с начальными условиями.

В нерекурсивном алгоритме этот цикл соответствует рекурсивному обращению к

146

себе, а подготовка цикла к действиям — занесению в магазин начальных данных с

которыми обращалась программа к рекурсивной процедуре.

Пример.

Пусть имеется рекурсивная функция обхода дерева:

void Obhod (TTree * T) ;

// Корневой обход дерева

{

if (T==NULL) return;

printf ("...",T->Data);

Obhod (T->Left);

Obhod (T->Right);

}

Отсутствие дополнительных действий между или после двух последовательных

рекурсивных вызовов функции Obhod(T − > Left) и Obhod(T − > Right) позволя-

ет хранить в магазине только ссылки на обрабатываемые вершины (и не заводить

специальные признаки, показывающие, что нужно делать с указанными ссылками).

#define MAX_MAG 100

typedef TTree TMag [MAX_MAG];

TMag Mag; // магазин

int uk=0; // указатель верхушки магазина

TTree h; // временная вершина

Mag[ uk ]= Root; // соответствует вызову Obhod(Root)

while ( uk >= 0 )

{

if (Mag[ uk ] == NULL) uk--;

else {

printf ("...",Mag[ uk ]->Data);

h= Mag[ uk ];

Mag[ uk++] = h->Right;

Mag[ uk ] = h->Left;

}

Если бы алгоритм обхода был другим, например, либо L → R → Root, либо

L → Root → R, то в магазин надо было бы дополнительно заносить признак, ука-

зывающий действие, которое необходимо выполнить над вершиной из верхушки ма-

газина. Таким действий может быть два: дальнейший обход, начиная с указанной

вершины, или печать информации о вершине.

6.3 Методы отсечения

Самый прямолинейный подход при поиске решений методом полного перебора

состоит в попытке перепробовать все различные ходы, пока не удастся получить

решение. Такого рода попытки по своей сути связаны с поиском при помощи проб

и ошибок. Отправляясь от начальной конфигурации задачи, мы можем построить

147

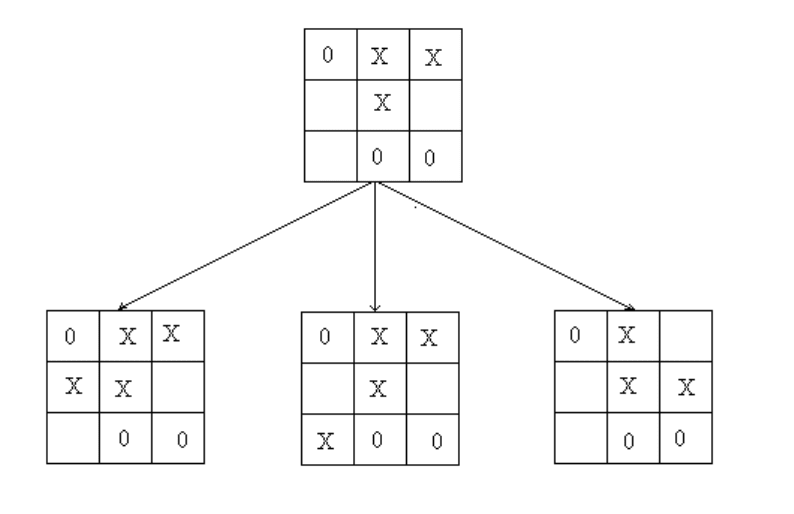
Рис. 6.3: Фрагмент дерева состояний игры КРЕСТИКИ — НОЛИКИ.

все конфигурации, возникающие в результате выполнения каждого из возможных

ходов, затем построить следующее множество конфигураций после применения сле-

дующего хода и т.д., пока не будет построена целевая конфигурация. Для поиска

такого рода методов поиска решения оказывается полезным введение понятия "со-

стояния" задачи. Например, для игры в "крестики-нолики" состояние задачи — это

просто конкретное расположение крестиков и ноликов в клетках таблицы. Простран-

ство состояний этой игры, достижимых из начального состояния, состоит из всех тех

конфигураций крестиков и ноликов, которые могут быть образованы по правилам

записи этих символов в клетки таблицы. Пространство состояний, достижимых из

данного начального состояния, полезно представлять в виде графа, вершины ко-

торого соответствуют этим состояниям, а дуги определяют один возможный шаг.

Например, для игры в "крестики-нолики" один шаг перехода в новое состояние для

очередного хода "крестиков" подграф переходов может имееть вид, представленный

на рис. 6.3.

Многие из прикладных задач имеют чрезвычайно большие пространства состоя-

ний, поэтому методы полного перебора всех вариантов практически неработоспособ-

ны из-за временных ограничений. Один из способов ускорения поиска решения со-

стоит в использовании оценочных функций для упорядочивания перебора вариантов.

Оценочная функция должна обеспечивать возможность упорядочивания вершин —

кандидатов на обработку — с тем, чтобы выделить ту вершину, которая с наибольшей

вероятностью находится на лучшем пути к цели. Оценочные функции строятся на ос-

нове различных соображений и связаны с конкретной прикладной областью. Один из

часто употребляемых вариантов определения функции цели основан на понятии рас-

стояния или другой меры различия между текущей вершиной и множеством целевых

вершин. Рассмотрим, например, игру в "восемь" как усеченный вариант известной

игры "пятнадцать". Имеется квадратное клеточное поле размером 3 на 3 и восемь

квадратных фишек с номерами от 1 до 8. Для произвольной расстановки фишек

требуется найти способ их передвижения так, чтобы в результирующей позиции все

фишки были упорядочены (см. рис. 6.4 ).

148

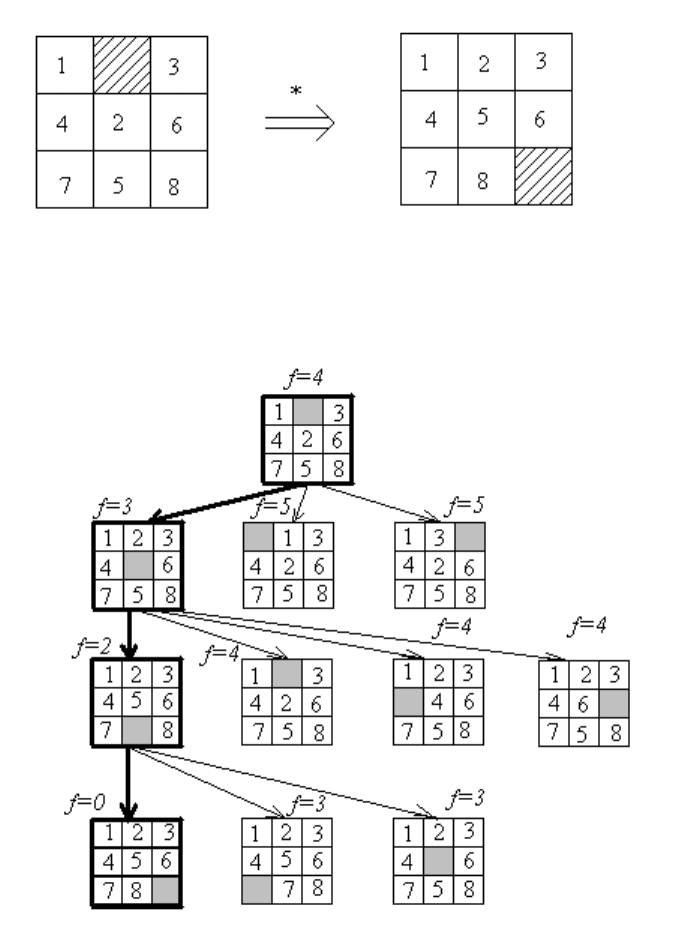
Рис. 6.4: Конечное состояние и вариант начального состояния игры в "восемь".

Рис. 6.5: Отсечение вариантов для игры в ВОСЕМЬ.

Выберем в качестве функции цели число позиций, на которых фишки стоят не

на своих местах, и будем перебирать вершины в порядке неубывания функции цели.

Тогда для начальной позиции рис. 6.4 порядок поиска решения представлен на рис.

6.5.

На каждом шаге существует не более четырех вариантов хода. Выбор лучшего

из них определяется минимальным значением функции цели. На рисунке рассмот-

рен вариант алгоритма выбора очередного хода без контроля возврата в состояние,

которое уже встречалась на пути решения. Реализовать такой контроль достаточно

просто, если хранить весь путь решения задачи. Следует, однако, отметить суще-

ственные затраты времени на полный такой контроль. Значительно легче отсекать

только возврат на один шаг назад в предшествующее состояние. Написать соответ-

ствующую программу предоставляется учащемуся в качестве упражнения.

149

6.4 Динамическое программирование

6.4.1 Понятие динамического программирования

Рекурсивная техника полезна, если задачу можно разбить на подзадачи, каж-

дая из которых решается за разумное время, т.е. суммарный размер задач будет

небольшим. Из формулы (4.1) оценки временной сложности вытекает, что если сум-

ма размеров подзадач задачи размера n равна an для некоторой постоянной a > 1, то

рекурсивный алгоритм, вероятно, имеет полиномиальную временную сложность. Но

если разбиение задачи размера n сводит ее к n задачам размера n − 1, то рекурсив-

ный алгоритм, вероятно, имеет экспоненциальную сложность. В этом случае часто

можно получить более эффективные алгоритмы с помощью специальной техники,

называемой динамическим программированием. Суть динамического програмирова-

ния основана на временном хранении в специальном массиве текущих решений на

задачах предшествующих размеров. Динамическое программирование, в сущности,

вычисляет решение всех подзадач. Вычисление идет от малых подзадач к большим,

и ответы запоминаются в таблице. Преимущество этого метода состоит в том, что

если уж подзадача решена, то ее ответ где-то хранится и никогда не вычисляется за-

ново. Рассмотрим применение метода динамического программирования на простых

примерах.

Пример 1.

Рассмотрим произвольную последовательность N целых чисел. Между числами

необходимо расставить знаки операций "+" или "−так что в результате получит-

ся некоторе арифметическое выражение. Это выражение всегда можно вычислить.

Пусть, например, имеется последовательность четырех чисел 17, 5, -21, 15. Суще-

ствует восемь различных выражений:

17 + 5 + -21 + 15 = 16,

17 + 5 + -21 - 15 = -14,

17 + 5 - -21 + 15 = 58,

17 + 5 - -21 - 15 = 28,

17 - 5 + -21 + 15 = 6,

17 - 5 + -21 - 15 = -24,

17 - 5 - -21 + 15 = 48,

17 - 5 - -21 - 15 = 18.

Назовем последовательность целых чисел "делимой" на K, если операции "+"

или "−" так можно разместить между этими числами, что результирующее значение

будет нацело делиться на K. В приведенном выше примере последовательность не

делится на 5, но делится на 7. Делимость на 7, например, следует из выражения

17 + 5 + −21 − 15 = −14

или из выражения

17 + 5 − −21 − 15 = 28.

Задача состоит в том, чтобы для заданного числа K проверить делимость на

него заданной последовательности. Пусть имеются следующие ограничения на зна-

чения исходных данных: 2 ≤ K ≤ 100, 1 ≤ N ≤ 10000, каждое число не больше

10000 по абсолютной величине. Очевидно, что решение задачи можно организовать

с помощью полного перебора всех вариантов простановки знаков операций между

числами и вычисления результирующей суммы. Процесс перебора всех возможных

1999-2000 ACM Notheastern European Regional Programming Contest

150