Крючкова Е.Н. Основы математической логики и теории алгоритмов
Подождите немного. Документ загружается.


13. Как для произволной частично–рекурсивной функции построить эквивалент-
ный алгоритм Маркова?
14. Перечислите известные Вам неразрешимые проблемы, имеющие непосред-
ственное отношение к практике программирования.
15. Сформулируйте теорему Райса.
16. Как используется метод сводимости для доказательства неразрешимости?
17. Как для произвольного алгоритма Маркова построить эквивалентную машину
Тьюринга?
18. Какие способы доказательства неразрешимости проблем Вы знаете?
19. Дайте формальное определение алгоритма.
20. Какие эквивалентные определения алгоритма Вы знаете?
4.9 Упражнения к разделу
4.9.1 Задача
Построить машину Тьюринга и алгоритм Маркова, вычисляющие функцию
f(x, y) =
2x + 3y
4
.
Решение. Очевидно, что на множестве натуральных чисел функция определе-
на не всюду, поэтому как для машины Тьюринга, так и для алгоритма Маркова
необходимо предусмотреть зацикливание в случае, когда 2x + 3y не кратно 4.
Рассмотрим сначала алгоритм Маркова. Очевидно, что умножение на некоторую
константу c в унарном коде реализуется с помощью замены каждой единицы на c
единиц. Для того, чтобы организовать умножение сначала на 2, а потом на 3, нужно
использовать разный маркер. Можно сначала перед цепочкой поставить, например,
маркер △, выполнить с этим маркером умножение на 2, а затем, когда закончат-
ся знаки "1" первого аргумента, заменить его на другой маркер, например, ⊕. Для
реализации деления полученной суммы на 4 потребуется еще один маркер. Исполь-
зуем для этой цели знак Ω. Поставим перед исходной цепочкой два маркера △ и Ω,
используя правило
ε → Ω△
Эта правило должно стоять последним в последовательности правил алгоритма.
Умножение последовательно на 2 и 3 реализуется правилами
△1 → 11△
△∗ → ⊕
⊕1 → 111 ⊕ .
Завершаем умножение, удаляя уже не нужный маркер:
⊕ → ε.
Теперь осталось с помощью маркера Ω реализовать деление:
Ω1111 → 1Ω.
101

Если имеется остаток, организуем зацикливание:
Ω1 → Ω1.
Эта команда может стоять только после предыдущей команды, т.к. по правилам вы-
полнения алгоритма Маркова выполняется первая применимая к цепочке команда.
Если остатка нет, завершаем вычисление функции:
Ω → ε
•
.
Таким образом, получили следующий алгоритм Маркова:
△1 → 11△
△∗ → ⊕
⊕1 → 111⊕
⊕ → ε
Ω1111 → 1Ω
Ω1 → Ω1
Ω → ε
•
ε → Ω △ .
Рассмотрим теперь машину Тьюринга, которая вычисляет эту же функцию. Если
ввести обозначения для вспомогательных функций
f
1
(x) = 2x, f
2
(x) = 3x, f
3
(x) =
x
4
, f
4
(x, y) = x + y,
то
f(x, y) = f
3
(f
4
(f
1
(x), f
2
(y))).
Теперь достаточно построить машины Тьюринга T
1
, T
2
, T
3
, T
4
, вычисляющие соответ-
ственно функции f
1
(x), f
2
(x), f
3
(x), f
4
(x, y), а затем с помощью композиции
T
left
1
· T
second
· T
right
2
· T
back
· T
3
· T
4
вычислить искомую функцию f(x, y). Здесь T
left
1
и T
right
2
— T
1
и T
2
, работающие
соответственно на левой и правой полуленте и воспринимажщие символ ∗ в качестве
разделителя ленты на полуленты. Вспомогательные машины Тьюринга T
second
и T
back
перемещают головку соответственно к началу второго аргумента и к началу всей
цепочки.
Построить указанные машины Тьюринга просто. Рассмотрим в качестве примера
построение T
4
. На вход в соответствии с определением машины Тьюринга, которая
вычисляет функцию двух аргументов, поступает цепочка 1
x
∗ 1
y
. Функция всегда
определена, поэтому для любых исходных данных после заверщения работы на лен-
те должна остаться цепочка 1
x+y
. Для этого достаточно заменить символ ∗ на 1, а
затем вернуть головку к началу цепочки и стереть первую единицу из получившей-
ся последовательности 1
x+y+1
. Указанные действия выполняет машина Тьюринга с
командами:
p
0
1 → p
0
1R, p
0
∗ → p
1
1L,
p
1
1 → p
1
1L, p
1
ε → p
2
εR,
p
2
1 → p
z
εR.
Эта машина Тьюринга представлена в виде графа на рис. 4.1.
Функция
f
3
(x) =
x
4
102
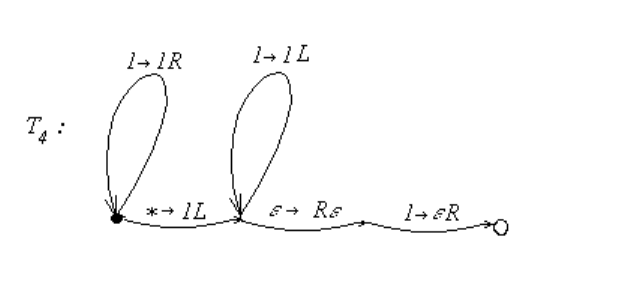
Рис. 4.1: Машина Тьюринга T
4
, вычисляющая функцию f
4
(x, y) = x + y.
определена только при условии, что значение переменной x кратно 4. Деление можно
реализовать с помощью переноса одной единицы за специально поставленный мар-
кер ∗ после чтения последовательности из четырех единиц. При чтении эти единицы
стираются. Если единицы закончились, то частное вычислено и остается только сте-
реть маркер. Если при чтении единиц на ленте остается одна, две или три единицы,
надо организовать зацикливание. Указанные действия выполняет машина Тьюринга
с командами:
p
0
ε → p
z
εE, p
0
1 → p
1
1L,
p
1
ε → p
2
∗ R,
p
2
1 → p
2
1R, p
2
∗ → p
2
∗ R,
p
2
ε → p
3
εL,
p
3
1 → p
4
εL, p
3
∗ → p
8
εL,
p
4
1 → p
5
εL, p
5
1 → p
6
εL, p
6
1 → p
7
εL,
p
7
1 → p
7
1L, p
7
∗ → p
7
∗ L,
p
7
ε → p
2
1R,
p
8
1 → p
8
1L, p
8
ε → p
z
εR.
В множестве команд мы не предусмотрели команды зацикливания, т.к. по опреде-
лению машина Тьюринга остается в неопределенном состоянии, если она оказалась
в такой конфигурации, в которой нет применимой команды. Такое неопределенное
состояние означает зацикливание машины Тьюринга. Явное указание зацикливания
можно указать, если в множество каманд включить команды
p
4
∗ → p
4
∗ E, p
5
∗ → p
5
∗ E, p
6
∗ → p
6
∗ E.
Эта же машина Тьюринга, представленная в виде графа, имеет вид, представ-
ленный на рис. 4.2.
103
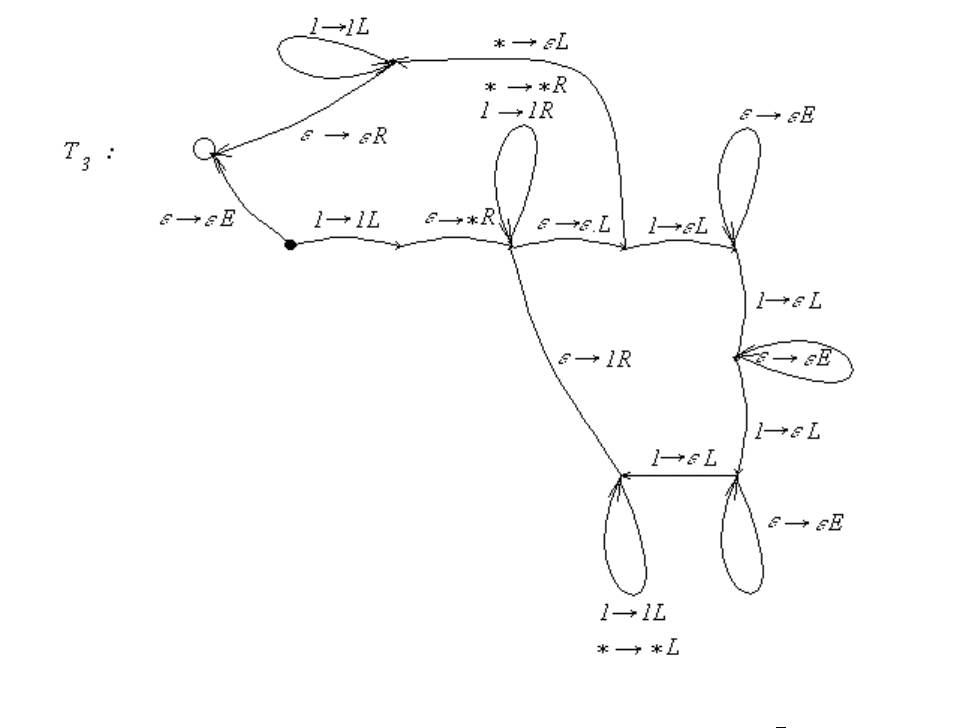
Рис. 4.2: Машина Тьюринга, вычисляющая функцию f
3
(x) =
x
4
.
104
4.9.2 Варианты заданий
1. f (x, y) =
{
x+2
y
, если y < 3
xy, если y ≥ 3
2. f (x, y) =
{
x−2
y
2
, если y < 3
x + y, если y ≥ 3
3. f (x, y, z) =
{
x−z
y
2
, если y < 3
x + z, если y ≥ 3
4. f (x, y, z) =
{
x−z
3
, если x + y < 4
x + y + z, если x + y ≥ 4
5. f (x, y, z) =
{
y − x − z, если z < 4
x+y
z
, если z ≥ 4
6. f (x, y, z) =
{
y −
x
z
, если z < 3
x+y+z
3
, если z ≥ 3
7. f (x, y, z) =
{
log
2
z, если z < 5
x+y
2
, если z ≥ 5
7. f (x, y) =
{
l og
2
x, если x < 8
x−y
2
, если z ≥ 8
7. f (x, y) =
{
√
x, если x < 7
x−3
y
, если x ≥ 7
8. f (x, y) =
{
√
x − y, если |x − y| < 5
x−3
y
, если |x − y| ≥ 5
9. f (x, y) =
{
x−2
y−1
, если y < 3
3x − y, если y ≥ 3
10. f (x, y) =
x−2
y−1
, если y < 3
3x, если 7 > y ≥ 3
2y, если y ≥ 7
11. f (x, y, z) =
z−2
y−1
, если x + y < 3
3 + x, если 7 > x + y ≥ 3
2 + y, если x + y ≥ 7
12. f (x, y, z) =
√
x + y − 2, если x + y < 8
x, если 10 > x + y ≥ 8
2x − z, если x + y ≥ 10
13. f (x, y) =
{
l og
3
x + y + 2, если x + y < 6
x − y, если x + y ≥ 6
105
14. f (x, y) =
{
l og
2
x + y + 2, если x + y < 8
(x − 6)
x−5
, если x + y ≥ 8
15. f (x, y, z) =
{
l og
3
x−y
3z
, если x + y < 7
z + (x − 5)
x−6
, если x + y ≥ 7
16. f (x, y, z) =
{
√
x−y
3−z
, если z < 7
z + 2, если z ≥ 7
16. f (x, y, z) =
√
x−y
3−z
, если z < 7
2, если z ≥ 7&x > 0
z
2
, если z ≥ 7&x = 0
17. f (x, y, z) =
√
log
2
z, если z < 7
2 + z + x − y, если z ≥ 7&x > 0
y
2
, если z ≥ 7&x = 0
18. f (x, y) =
{
√
x +
√
x − 2, если x < 5
y
2x
, если x ≥ 5
19. f (x, y, z) =
√
1 +
√
x, если x < 4
z, если x = 4
y
2+x
, если x > 4
20. f (x, y) =
x
x−2
, если x < 4
x − y, если x = 4
x+1
2
, если x > 4
4.10 Тесты для самоконтроля к разделу
1. Какую функцию двух аргументов вычисляет алгоритм Маркова со следующи-
ми правилами:
∗1 −→ 11
•
∗ −→ 11∗
Варианты ответов:
а) f (x, y) = x + y + 1.
б) f (x, y) =
{
x + 1, y > 0
0, y = 0
в) f (x, y) =
{
x + 1, y > 0
∞, y = 0
г) f (x, y) = ∞.
д) f (x, y) = {y + 1, x = 0∞, x > 0
Правильный ответ: в.
2. Задать Геделевскую нумерацию объектов множества M — это значит выпол-
нить следующие действия:
1) указать алгоритм, который для каждого элемента x ∈ M однозначно вычис-
ляет целое число – номер элемента x;
106
2) указать алгоритм, который для каждого натурального числа n либо выдает
восстановленный по номеру n элемент x ∈ M, либо зацикливается (при устовии, что
число n не является номером какого-либо элемента множества M );
3) указать алгоритм, который для каждого натурального числа n выдает одно из
двух сообщений: либо восстановленный но n элемента x ∈ M, либо сообщение о том,
что число n не является номером какого-либо элемента множества M.
Правильный ответ: 1 и 3.
3. Какие проблемы из перечисленных ниже проблем неразрешимы?
1) Проблема эквивалентности алгоритмов Маркова и частично–рекурсивных функ-
ций.
2) Проблема переводимости.
3) Проблема остановки машины Тьюринга.
Правильный ответ: 2 и 3.
4. Какие из следующих утверждений истинны?
1) Если функция f построена с помощью ограниченного оператора минимиза-
ции из примитивно-рекурсивных функций, то f может быть вычислена на машине
Тьюринга.
2) Если существует машина Тьюринга, правильно вычисляющая функцию f, то
эта функция может быть построена с помощью ограниченного оператора минимиза-
ции из примитивно-рекурсивных функций.
3) Если функция вычислима алгоритмом Маркова, то она является примитивно—
рекурсивной.
Правильный ответ: только 1.
5. Теорема Райса — это теорема
а) о неразрешимости проблемы остановки машины тьюринга;
б) об эквивалентности алгоритмов Маркова и машин Тьюринга;
в) об эквивалентности алгоритмов Маркова и примитивно—рекурсивных функ-
ций;
г) о неразрешимости проблемы эквивалентности частично–рекурсивных функций
и машин Тьюринга;
д) о неразрешимости проблемы распознавания нетривиальных свойств множе-
ства.
Правильный ответ: д.
107
Глава 5
ТЕОРИЯ СЛОЖНОСТИ
АЛГОРИТМОВ
5.1 Понятие временной и емкостной сложности ал-
горитмов
Для того, чтобы оценить сложность алгоритма, необходимо сначала выбрать
характеристику, которая определяет величину исходных данных или их количество.
Такая характеристика называется размером задачи. Выбор размера задачи главным
образом определяется формулировкой этой задачи. Например, для любой машины
Тьюринга в качестве размера задачи удобно выбрать длину исходной цепочки, а в
задаче, алгоритм решения которой построен на основе обработки графа, для этой
цели обычно используется число вершин соответствующего графа.
Время работы алгоритма и используемую алгоритмом память можно рассматри-
вать как функции размера задачи n. Обычно рассматривают следующие функции
сложности алгоритма:
T (n) — временная сложность,
C(n) — емкостная сложность.
Единицы измерения T (n) и C(n) зависят от типа исследуемой алгоритмической
модели.
Обычно при выполнении алгоритма над разными исходными данными, имеющи-
ми один размер, время работы и используемая память зависят еще и от значения
этих данных. Поэтому, чтобы сделать функции сложности независимыми от кон-
кретных значений данных, как правило, рассматривают не точную аналитическую
зависимость T или C от n, а оценки сложности: максимальную T
max
(n) или C
max
(n),
среднюю T
mid
(n) или C
mid
(n). Причем часто представляют интерес даже не точ-
ное аналитическое представление функциональной зависимости, например T
max
(n),
а просто порядок сложности алгоритма.
Определение 5.1.
Функция f(n) есть O(g(n)), если существует константа C такая, что |f(n)| <
C|g(n)| для всех n > 0.
Запись f (n) = O(g(n)) читается: "функция f(n) имеет порядок g(n)". Полиноми-
альным алгоритмом (или алгоритмом полиномиальной временной сложности) назы-
вается алгоритм, у которого
T (n) = O(p(n)),
где p(n) — некоторая полиномиальная функция. Алгоритмы, временная сложность
которых не поддается подобной оценке, называются экспоненциальными. Различие
108
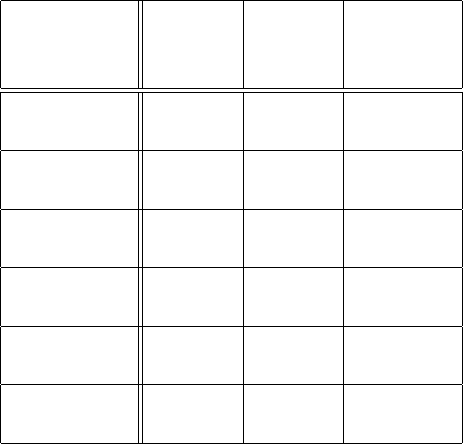
Таблица 5.1
Зависимость времени работы программы
от сложности задачи
Функция
временной n = 10 n = 30 n = 60
сложности
n 0.00001 0.00003 0.00006
сек. сек. сек.
n
2
0.0001 0.0009 0.0036
сек. сек. сек.
n
3
0.001 0.027 0.216
сек. сек. сек.
n
5
0.1 24.3 13.0
сек. сек. мин.
2
n
0.001 17.9 366
сек. мин. столетий
3
n
0.059 6.5 13 · 10
13
сек. лет столетий
между двумя указанными типами алгоритмов становится особенно заметным при
решении задач большого размера. В таблице 5.1 приведены скорости роста некоторых
типичных полиномиальных и экспоненциальных функций.
Разные алгоритмы имеют разную временную сложность, и выяснение того, какие
алгоритмы "достаточно эффективны а какие "совершенно неэффективны всегда бу-
дет зависеть от конкретной ситуации. Однако различие между полиномиальными и
экспоненциальными алгоритмами становится настолько заметным при решении за-
дач большого размера, что становятся ясными причины, по которым понятие "труд-
норешаемости" отождествляется с экспоненциальным характером функции времен-
ной сложности. Именно временная сложность алгоритма определяет в итоге размер
задач, которые можно решить этим алгоритмом. Разные алгоритмы имеют различ-
ную временную сложность T (n) и влияние того, какие алгоритмы достаточно эффек-
тивны, а какие нет, всегда зависит как от размера задачи, так и от порядка временной
сложности, а при небольших размерах еще и от коэффициентов в выражении T (n).
Можно было бы подумать, что колоссальный рост скорости вычислений, вызван-
ный появлением нового поколения компьютеров, уменьшит значение эффективных
алгоритмов. Однако происходит в точности противоположное. Так как вычислитель-
ные машины работают все быстрее и мы можем решать все большие задачи, именно
сложность алгоритма определяет то увеличение размера задачи, которое можно до-
стичь с увеличением скорости машины. Различие между полиномиальными и экспо-
ненциальными алгоритмами становится еще более убедительным, если проанализи-
ровать влияние увеличения быстродействия ЭВМ на время работы алгоритмов.
Пусть n — размер задачи при использовании старой техники, m — размер задачи
при использовании новой техники. Тогда из условия, что задача решается за одно
и то же время на старой и новой технике, следует равенство функций временной
сложности для разных размеров задачи:
T
old
(n) = T
new
(m).
109
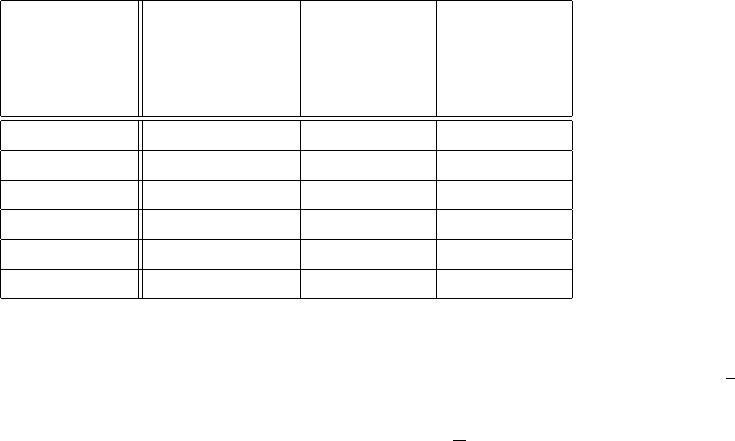
Таблица 5.2
Зависимость размеров задач от
быстродействия ЭВМ
Функция На На ЭВМ в На ЭВМ в
временной современной 100 раз 1000 раз
сложности ЭВМ более более
быстрых быстрых
n n
1
100n
1
1000n
1
n
2
n
2
10n
2
31.6n
2
n
3
n
3
4.64n
3
10n
3
n
5
n
4
2.5n
4
3.98n
4
2
n
n
5
n
5
+ 6.64 n
5
+ 9.97
3
n
n
6
n
6
+ 4.19 n
6
+ 6.29
Но скорость новой машины в k раз выше, следовательно T
new
(m) =
1
k
T
old
(m). Отсюда
T
old
(n) =
1
k
T
new
(m),
откуда можно получить соотношение m = f(n) для определения нового размера
задачи, решаемой за то же время на новой технике.
Примеры роста размеров задач при увеличении скорости компьютера для некото-
рых полиномиальных и экспоненциальных зависимостей функции временной слож-
ности приведены в таблице 5.2. Эти данные получены для задач, решаемых за один
час машинного времени, если быстродействие ЭВМ возрастает в 100 или 1000 раз по
сравнению с современными компьютерами.
Таким образом, таблицы 5.1, 5.2 наглядно демонстрируют некоторые причины,
по которым полиномиальные алгоритмы считаются более предпочтительными по
сравнению с экспоненциальными.
Сколько вычислений должна потребовать задача, чтобы мы сочли ее труднореша-
емой? Общепринято, что если задачу нельзя решить быстрее, чем за полиномиаль-
ное время, то ее следует рассматривать как труднорешаемую. Тогда при такой схеме
классификации задачи, решаемые алгоритмами полиномиальной сложности, будут
легко решаемыми. Но нужно иметь в виду, что хотя экспоненциальная функция
(например, 2
n
) растет быстрее любой полиномиальной функции от n, для неболь-
ших значений n алгоритм, требующий O(2
n
) времени, может оказаться эффективнее
многих алгоритмов с полиномиально ограниченным временем работы. Например,
функция 2
n
не превосходит n
10
до значения n, равного 59. Тем не менее, скорость ро-
ста экспоненциальной функции столь стремительна, что обычно задача называется
труднорешаемой, если у всех решающих ее алгоритмов сложность по меньшей мере
экспоненциальна.
5.2 Практическая оценка временной сложности
Любая программа состоит из элементов трех типов: последовательно выполняю-
щихся участков, циклов и условных операторов, каждый из которых, в свою очередь,
может иметь сложную структуру и представлять собой такие же элементы. Очевид-
но, что время работы последовательного участка равно сумме времени выполнения
110
