Красильников Н.Н., Красильникова О.И. Мультимедиа технологии в информационных системах. Методы сжатия и форматы записи графической информации

Подождите немного. Документ загружается.

Второй метод состоит в том, что сохраняются только те спектраль-

ные коэффициенты, амплитуда которых превышает заранее установ-

ленный порог. Этот метод отбора сложнее зонального, поскольку, кро-

ме передачи (записи) значений спектральных коэффициентов,

необходимо также передавать (записывать) их индексы.

Перед тем, как переходить к более детальному рассмотрению метода

сжатия данных, основанного на применении ортогональных преобразо-

ваний, сравним его с ДКИМ. Общим для этих двух методов является

двухэтапная обработка изображений, включающая в себя декорреляцию

и последующее оптимальное кодирование сигнала. Важное различие

между ДКИМ и методом сжатия с использованием ортогональных пре-

образований состоит в том, что в первом случае имеет место декорре-

ляция за счет предсказания, при которой используется «локальная» ста-

тистика изображения, а во втором – декорреляция за счет укрупнения,

и, следовательно, используется «средняя» статистика изображения. При

передаче стационарных изображений эта особенность не играет роли, и

оба метода сжатия дают близкие результаты. Если изображение неста-

ционарно, как например при передаче мелкомасштабного объекта на

фоне поля с медленно изменяющейся яркостью, это различие в способе

декорреляции весьма существенно. На той части изображения, где рас-

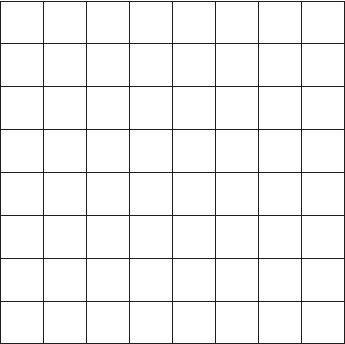
01234567

021 7532100

177532100

255532100

333332100

422222100

511111100

600000000

700000000

v→

→

Рис. 10

положен мелкомасштабный объект, «текущее» значение коэффициента

автокорреляции между сигналами от соседних отсчетов невелико

()

( 0,5...0,7).

ρτ=

Поэтому его сжатие посредством ДКИМ оказывает-

ся неэффективным. В то же время значение коэффициента автокорре-

ляции

()

сэ

усредненное по всему изображению, может быть близ-

ким к единице, благодаря чему будет обеспечиваться высокая

эффективность сжатия методом, использующим ортогональные преоб-

разования. Рассмотрим более подробно ортогональные преобразования

предварительно дискретизированных изображений, представляемых в

виде массива (матрицы) чисел

()

Lkn

размером

где k –

номер строки; n – номер столбца (номер отсчета в строке). Следует

обратить внимание на то, что в этой записи порядок указания коорди-

нат точки отсчета яркости на изображении изменен на обратный, то

есть вместо обозначения

()

Lxy

мы пишем

()

Lkn

Это делается

для согласования с формой записи, принятой в матричном анализе, где

первая координата обозначает номер строки, а вторая – номер столбца.

Спектральные коэффициенты

()

,Fuv

находятся путем прямого орто-

гонального преобразования изображения следующим образом:

() ()( )

,,,,,,

Fuv L knaknuv

−−

∑∑

где

()

,,,aknuv

– ядро прямого преобразования (базисные функции, по

которым происходит разложение);

,uv

– индексы спектральных коэф-

фициентов, определяющие их принадлежность в соответствующей ба-

зисной функции, а также положение в матрице спектральных коэффи-

циентов, которая имеет тот же размер, что и преобразуемое изображение.

Исходное изображение (массив чисел

()

Lkn

) находится путем об-

ратного ортогонального преобразования:

() ()( )

,,,,,,

Lkn Fuvbknuv

−−

∑∑

где

()

,,,bknuv

– ядро обратного преобразования. Если преобразова-

ние разделимо:

()()()

стр

,,, , , ,

aknuv a kua nv

()()()

стр

,,, , ,

bknuv b kub nv

(а нас будут интересовать разделимые преобразования), то оно может

быть выполнено в два этапа (вначале – по всем столбцам, а затем – по

всем строкам):

() () ()()

стр 0

,,,,,

сэ

Fuv a nv L kna ku

−−

∑∑

(3.5)

и соответственно

() () ()()

стр

,,,,.

сэ

Lkn b nv Fuvbku

−−

∑∑

(3.6)

Для удобства записи и вычислений используют матричный аппарат.

В матричной форме разделимые ортогональные преобразования запи-

сываются следующим образом:

эс0стр

с0 э стр

bFb

(3.7)

где a

, a

стр

– ортогональные матрицы прямого преобразования по стол-

бцам и строкам, b

стр

– ортогональные матрицы обратного преобразо-

вания по столбцам и строкам,

стр

– матрицы, полученные в

результате транспонирования матриц

стр

() () ( )

00 01

с0

01 01 011

1,1 1, 2 ... 1,

2,1 2,1 ... 2,

... ... ... ...

,1 , 2 ... ,

сс с

LL LN

LN LN LNN

где F – матрица спектральных коэффициентов, получаемая в результате

двумерного ортогонального преобразования.

() () ( )

()() ( )

11 11

F 1,1 F 1, 2 ... F 1,

F2,1 F2,1 ... F2,

... ... ... ...

F,1F,2...F,

NN NN

Учитывая, что

ээ

−

стр стр

−

а также соотношения

ээ

−

стр стр

−

справедливые для ортогональных матриц, имеем:

TT T

с0 э стр э стр





aa aa

(3.8)

где

−

стр

−

– матрицы, полученные в результате обращения матриц

эстр

Базисные функции

()

стр

anv

()

,,aku

()

стр

bnv

()

bku

в фор-

мулах (3.5) и (3.6) или, что то же самое, ортогональные матрицы в фор-

мулах (3.7) и (3.8) определяются применяемым ортогональным преобра-

зованием. Так, например, в случае двумерного дискретного

преобразования Фурье (ДПФ) базисные функции представляют собой

комплексные экспоненты, а сами ортогональные преобразования име-

ют вид:

() () ()

с0

,,exp

Fuv L kn uk vn

−−



=−+





∑∑

() () ()

с0

,,exp,

Lkn Fuv ukvn

−−







∑∑

где множитель

имеет смысл пространственной частоты,

=−

Известно, что ДПФ не является лучшим преобразованием для при-

менения в целях сжатия данных, так как значения спектральных коэф-

фициентов в области высоких пространственных частот при этом пре-

образовании имеют сравнительно высокие значения. В настоящее время

при сжатии изображений широкое распространение получило дискрет-

ное косинусное преобразование (ДКП). Среди других ранее применяв-

шихся ортогональных преобразований при сжатии изображений: преоб-

разование Адамара (ПА), преобразование Хаара (ПХ), наклонное

преобразование (slant transform).

Ортогональные преобразования изображений допускают ряд следу-

ющих интерпретаций.

Во-первых, двумерное преобразование изображения можно рассмат-

ривать как его разложение в обобщенный двумерный спектр, а спект-

ральные коэффициенты – как амплитуды соответствующих спектраль-

ных составляющих. Если применяются негармонические базисные

функции, как, например, в случае преобразования Адамара, понятие

частоты необходимо обобщить и пользоваться понятием секвенты. На-

помним, что секвентой (ненормированной) называется величина, рав-

ная половине среднего числа пересечения нуля в единицу времени (на

единицу длины).

Другая возможная интерпретация обусловлена тем, что матрица пре-

образуемого изображения и матрицы базисных изображений имеют оди-

наковые размеры, то есть состоят из одного и того же числа строк и

столбцов. Это дает возможность спектральные коэффициенты рассмат-

ривать как весовые коэффициенты, с которыми необходимо просумми-

ровать базисные изображения, чтобы получить исходное изображение.

Спектральные коэффициенты можно также рассматривать и как функ-

ции взаимной корреляции между преобразуемым изображением и соот-

ветствующими базисными изображениями.

И, наконец, ортогональные преобразования можно рассматривать как

такой поворот N – мерной системы координат

(),NNN

=×

в которой

преобразуемое изображение, состоящее из N отсчетов, представляется

N – мерным вектором, при котором корреляция между его компонента-

ми сводится к минимуму.

Важным свойством ортогональных преобразований является сохра-

нение метрики. Благодаря этому свойству евклидово расстояние между

изображениями равно евклидову расстоянию между их образами (спек-

тральными отображениями).

3.3. Дискретное косинусное преобразование

Двумерное дискретное косинусное преобразование является разде-

лимым и может быть выполнено по формулам:

() ()() ( )

с0

cos cos ,

Fuv cucv L kn

uk vn

−−

=×



ππ

 

×+ +

 



 



∑∑

(3.9)

() ()() ( )

cos cos ,

Lkn cucvFuv

uk vn

−−

=×



ππ

 

×+ +

 



 



∑∑

(3.10)

где функции

()

определены следующим образом:

()

012,

()

w =

при

1, 2,..., 1.

=−

На рис. 11 приведены

одномерные базисные функции ДКП для случая, когда

Как из-

вестно, вычисление двумерного дискретного косинусного преобразова-

ния по приведенным формулам требует для его выполнения

опера-

ций умножения и сложения, что создает серьезную проблему, поскольку

значения

для реальных изображений составляют несколько сотен.

В связи с этим были предприняты исследования, направленные на со-

кращение требуемого объема вычислений. В результате этих исследо-

ваний были разработаны два дополняющих друг друга метода.

Первый метод заключается в том, что кодируемое изображение раз-

мером

стр пикс

NN×

отсчетов предварительно разбивается на отдельные

блоки размером

бл бл

отсчетов, а затем независимо каждый из бло-

ков подвергается дискретному косинусному преобразованию. Посколь-

ку каждый блок содержит в

()

0 стр пикс бл

kNN N

=×

раз меньше отсче-

тов, чем исходное изображение, то на его преобразование в соответствии

с формулами (3.9, 3.10) потребуется уже не

()

стр пикс

NN×

операций (в

случае, когда

стр пикс 1

NN N

потребовалось бы соответственно

операций), а только

()

стр пикс 0

NN k×

вычислительных операций.

Учитывая, что все изображение содержит k

блоков, находим количе-

ство вычислительных операций, которые необходимо выполнить, что-

бы осуществить преобразование всего изображения

()

стр пикс 0

NN k

то есть в k

раз меньше, чем без разбиения на блоки. Поясним изложен-

ное примером. Предположим, что исходное изображение имеет размер

576×720

отсчетов, а размер блока составляет

16×16

отсчетов. Тогда в

соответствии с приведенными выше рассуждениями без разбиения изоб-

ражения на блоки потребовалось бы 171992678400 вычислительных опе-

раций, при разбиении изображения на блоки – 106168320, то есть в

1620 раз меньше, чем в первом случае. Следовательно, чем более мел-

кими будут блоки, тем большим будет их число k

и тем большим будет

сокращение числа операций, необходимых для выполнения ортогональ-

ного преобразования (в данном случае ДКП). Однако, как показывает

детальный анализ этой проблемы, делать блоки меньшими, чем

16×16

или, в крайнем случае,

8×8

отсчетов, не следует, так как корреляцион-

ные связи в изображении распространяются примерно на этот интер-

вал и дальнейшее уменьшение размеров блоков повлечет за собой уве-

личение амплитуд спектральных коэффициентов

()

,Fuv

с большими

индексами

,uv

и, как следствие, уменьшение сжатия данных.

Второй метод сокращения требуемого объема вычислений при вы-

полнении дискретного косинусного преобразования состоит в приме-

нении быстрого алгоритма вычисления ДКП, при котором требуемый

объем вычислений (умножений и сложений) сокращается с

()

до

()

121

log .

Поясним эффективность этого метода на примере, полагая, что раз-

мер блока составляет

16×16

×=

отсчетов изображения. При не-

посредственном вычислении спектральных коэффициентов по форму-

лам (3.9, 3.10) потребовалось бы выполнить 65536 операций умножения

и сложения. Используя быстрый алгоритм, потребуется выполнить 2048

операций, то есть в 32 раза меньше, чем в первом случае.

01234567

Номер базисной

функции

Рис. 11

В настоящее время при выполнении ДКП используют оба описан-

ные метода сокращения количества вычислительных операций, посколь-

ку они, дополняя друг друга, позволяют существенно ускорить вычис-

ления.

3.4. Оптимальное распределение двоичных единиц кода

между спектральными коэффициентами

Как уже отмечалось, в методе, использующем ортогональные преоб-

разования, сжатие данных достигается за счет того, что спектральные

коэффициенты, энергия которых мала, квантуются на меньшее число

уровней, а, следовательно, на их представление затрачивается меньшее

число двоичных единиц кода, чем на представление спектральных ко-

эффициентов с большой энергией.

Рассмотрим задачу распределения двоичных единиц кода между спек-

тральными коэффициентами

()

,Fuv

, при котором обеспечивается наи-

меньший средний квадрат шума преобразования

ш.кв

, обусловленно-

го квантованием (или отбрасыванием) спектральных коэффициентов

[1]. Будем считать, что сжимаемое изображение является черно-белым

полутоновым, а также, что нам заданы: размер блока

бл бл

, требу-

емый коэффициент сжатия k

сж

и значения средних квадратов спект-

ральных коэффициентов

()

,Fuv

Определим вначале число двоичных единиц кода

, которым мы

располагаем при заданном коэффициенте сжатия и которое нам пред-

стоит распределить между спектральными коэффициентами блока. Ис-

ходя из того, что для представления каждого пиксела в блоке исходного

черно-белого полутонового изображения требуется один байт, то есть 8

двоичных единиц, найдем, что для представления всего блока без сжа-

тия расходуется

бл

двоичных единиц кода. Следовательно, при за-

данном значении коэффициента сжатия k

сж

мы располагаем

()

бл сж

NNk

=×

количеством двоичных единиц кода, которые дол-

жны распределить между спектральными коэффициентами.

Как уже указывалось, средний квадрат шума квантования прямо про-

порционален среднему квадрату квантуемого сигнала. Применительно

к рассматриваемому случаю это значит, что средний квадрат шума кван-

тования спектрального коэффициента

()

,Fuv

будет равен

() ()()

кв

222

,,,,

uv F uv n W

σ= σ

(3.11)

где

()

– средний квадрат шума квантования сигнала на

уровней, при условии, что средний квадрат самого квантуемого сигна-

ла равен единице, а распределение его по яркости описывается плотно-

стью вероятности W, n

– число двоичных единиц кода. Средний квад-

рат шума преобразования (квантования) равен сумме средних квадратов

шумов, возникающих при квантовании каждого спектрального коэф-

фициента:

()

кв

ш.кв

σ= σ

∑∑

(3.12)

Чтобы обеспечить минимальное значение

ш.кв

поступим следую-

щим образом. Вначале выделим для представления каждого спектраль-

ного коэффициента нулевое количество двоичных единиц кода и най-

дем значения средних квадратов шумов квантования, которые при этом

возникают. Поскольку в этом случае мы совершили усечение (отбрасы-

вание) спектральных коэффициентов, значения средних квадратов шу-

мов квантования будут равны средним квадратам самих спектральных

коэффициентов, то есть

() ()

кв

,,,

uv F uv

σ=

ш.кв

– их сумме. За-

тем выбираем из всех значений

()

кв

самое большое, выделяем

спектральному коэффициенту, которому соответствует это самое боль-

шое значение среднего квадрата шума квантования, одну двоичную еди-

ницу кода, уменьшаем

на единицу и рассчитываем для него по

формуле (3.11) новое значение среднего квадрата шума квантования

()

кв

. После этого снова сравниваем между собой все значения

()

кв

, опять находим наибольшее и снова выделяем одну двоич-

ную единицу кода наиболее “шумящему” спектральному коэффициен-

ту, уменьшая при этом

на единицу. Так повторяем до тех пор, пока

не будут израсходованы все двоичные единицы кода

. При таком

распределении двоичных единиц мы обеспечиваем минимальный уро-

вень шума преобразования. Заключительным этапом описанной проце-

дуры является объединение спектральных коэффициентов, для пред-

ставления которых выделено одинаковое количество двоичных единиц

кода, в зоны.

Обратим внимание, что описанный метод распределения двоичных

единиц кода между спектральными коэффициентами еще не гарантиру-

ет минимальной заметности шума преобразования на изображении после

его декодирования. Объясняется это тем, что различные спектральные

компоненты по-разному воспринимаются зрительной системой. Поэто-

му, чтобы достичь минимальной заметности шума преобразования на

декодированном изображении, описанную процедуру необходимо вы-

полнять, используя для этого не средние квадраты шума квантования, а

их средневзвешенные значения.

Рассмотрим, как проявляется шум квантования, а также внешний

шум на декодированных изображениях. Поскольку результирующий уро-

вень шума преобразования является результатом одновременного воз-

действия всех шумовых компонентов, возникающих при квантовании

спектральных коэффициентов, то в силу центральной предельной тео-

ремы его распределение будет близким к нормальному. Так как средние

квадраты шума квантования всех спектральных коэффициентов близки

между собой вследствие примененной стратегии распределения двоич-

ных единиц, его спектральный состав будет близок к спектральному

составу квазибелого шума. Что касается проявления на изображении

внешней помехи при его передаче по каналу связи в сжатом виде, то

здесь все зависит от ее характера. Например, редкая импульсная помеха

проявляется в том, что отдельные блоки изображения передаются не-

верно, поэтому на них пропечатываются базисные изображения, соот-

ветствующие тем спектральным коэффициентам, которые были переда-

ны с ошибкой.

3.5. Вейвлет-преобразование

Вейвлет-преобразования применяются при сжатии изображений [1,

2]. Термин Wavelet переводят обычно как короткая волна или всплеск.

При вейвлет-преобразовании спектр исходного сигнала разделяется

на низкочастотную и высокочастотную компоненты с использованием

в качестве импульсных характеристик соответствующих фильтров, так

называемых вейвлет- и скейлинг-функций [4]. Поясним сказанное на

простейшем примере, когда исходная последовательность отсчетов, на-

пример значений яркости пикселов на строке изображения, разбивает-

ся на пары

()

2Lk

()

21,

Lk+

используя которые, вычисляют две

последовательности

()

одна из них представляет собой

полусуммы отсчетов

()

21,

Lk+

а вторая – полуразности, то

есть

() ( ) ( )

сс

2212,

kLkLk

=++



