Корянов А.Г. Математика. ЕГЭ 2010. Задания типа С1-С5. Методы решения

Подождите немного. Документ загружается.

.  2010.

1-5.

.

.

. , 2010, 138 .

  .  1999      

   () . .    

        .

.

 2000-2005  -    ,  2009  - 

.  2009  "

". e-mail: akoryanov@mail.ru



1

 42 .  2 .

 2





1. 

2. 

3. 

4. 

5. 

6. 

 ()

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

3



1. 

) ;

) ;

) ;

) , 

2. 

3. 

4. 

5. 

6. 

7. 

) ;

) ;

) ;



4



1. :

) ;

) ;

) , .

2. :

)  ();

) ;

) ,  (, 

);

) ;

) ;

) ,  ( – , );

) ,  (

);

) ,  (

);

)  ();

)  ();

)  (

)

:





, 







 (, , )

, 



















 ()



, 

























5





1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 



 

22. 

23. 

24. 

25. 

 

26. 

27.  ()





1. 

1.1. 

1.2. 

1.3.  ()

1.4. 

1.5. 

1.6. 

2. 

3. 

3.1. 

3.2.  F(x;y) = px + qy + r

3.3. 

3.4.  F(x; y) 

3.5. , 

3.6. 

3.7. 

3.8. 

МАТЕМАТИКА ЕГЭ 2010

Задания С1 и С2

Корянов А.Г. г.Брянск

Задания С1

● (Д – 2010) Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=−+−+

xxxx

sin22

7133

Ответ: ,2=x .,

)1( Znny

∈+⋅−=

1. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=+−

=+⋅

−

0cos45

5455

tgytgy

Ответ:

.,2

;13 Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

2. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

tgx

cos

0sin22

Ответ:

.,5,0;2

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

3. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=++

=+⋅−

01cos5

04254

sinsin

Ответ:

()

.,2;16 Znn ∈+

4. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=++−

=+−

0sin4164

05cos12cos4

xyy

Ответ:

.,2;2

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

5. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=−−

=−+

01sinsin

cos2cos

xxy

Ответ:

;,2;2

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

.,2;2

Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

6. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−=

=+⋅−

2cos

0162104

Ответ:

(

)

.,3;2 Znn

∈

7. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=+⋅−

0sin2

01641016

coscos

Ответ:

.,3;2

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

8. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−

1cos43

cos23

Ответ:

.,1;2

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

−+±

9. Решите систему уравнений

⎩

⎨

⎧

−=

2cos

3sin

Ответ:

(

)

;,3;2 Znn

∈

.,2;2

Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

10. Решите систему уравнений

⎩

⎨

⎧

−=

7cos

6sin

Ответ:

(

)

;,2;6 Znn ∈

.,2

;7 Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

11. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−

1sin22

sin2

Ответ:

)1(;1 Znn

∈

⎟

⎠

⎞

⎜

⎝

⎛

+⋅−−

12. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=+⋅−

0cos2

08193081

sinsin

Ответ:

.,2

;3 Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

13. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=+−

=−+

0cos4

02sin3sin2

yxx

Ответ:

;,2

;3 Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

.,2

;4 Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

14. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=++

0cos66

12cossin3

xyy

Ответ:

;,3;2

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

;,9;2

Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

−+

15. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=+−

−=−+−

0162

216442

xyy

yxyxyx

Ответ: ).4;4(−

16. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=+−

−=−+−

01004

2522

xyx

xyxxyy

Ответ: ).5;10( −−

17. Решите систему уравнений

⎩

⎨

⎧

=+−

135sin6

03sin7sin2

Ответ:

.,2;

)1( Znn

∈

⎟

⎠

⎞

⎜

⎝

⎛

+⋅−

18. Решите систему уравнений

⎩

⎨

⎧

=+−

=++

04cos2cos5

05cos11cos2

Ответ:

.,,2

;2 ZkZnkn ∈∈

⎟

⎠

⎞

⎜

⎝

⎛

+±+

ππ

19. Решите систему уравнений

⎩

⎨

⎧

832

1252

ytgx

Ответ:

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+ ,2;

20. Решите систему уравнений

⎩

⎨

⎧

7cos83

5cos43

ytgx

Ответ:

.,,2

;

ZkZnkn ∈∈

⎟

⎠

⎞

⎜

⎝

⎛

+±+

21. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=−−

02sin3sin2

0cos23

Ответ:

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

22. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=−−

03cos4cos4

0sin23

Ответ:

;,2

;

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

23. Решите систему уравнений

⎩

⎨

⎧

sin21

1sin8

Ответ:

(

)

;,;1 Znn

∈

−

24. Решите систему уравнений

⎩

⎨

⎧

cos21

1cos4

Ответ:

.,1;

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

−+

25. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

1cos2sin2

0sincos

Ответ:

.,,

;

)1( ZkZnkn

∈∈

⎟

⎠

⎞

⎜

⎝

⎛

++⋅−

26. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

3cos2sin2

0cossin

Ответ:

;,,;2

ZkZnkn ∈∈

⎟

⎠

⎞

⎜

⎝

⎛

+±

ππ

.,,

;

ZkZnkn ∈∈

⎟

⎠

⎞

⎜

⎝

⎛

+±+

27. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=+−−

=−−

0sin23

03cos4cos4

xyy

Ответ:

;,3;2

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

.,2;2

Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

−+−

28. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=−

yxx

sin22

cos2cos

Ответ:

(

)

;2;0 n

(

)

;2;2 n

⎟

⎠

⎞

⎜

⎝

⎛

+ n

.,2

;1 Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

29. Решите систему уравнений

⎩

⎨

⎧

ctgyx

tgyx

Ответ:

;33 Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

;33 Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−−

30. Решите систему уравнений

⎩

⎨

⎧

−=

ctgxy

tgxy

Ответ:

;,32;

Znn ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

.,32;

Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

−+

31. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−=

−

3sin4

cos2sin

Ответ:

.1,,2

=∈+= yZnnx

32. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−

3sin4

cos2sin

Ответ:

.7,,2

=∈+= yZnnx

33. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=−

+−

0cos

1sin3sin2

Решение. Из первого уравнения системы следу-

ет

01sin3sin2

=+− xx

и 0>y . Пусть

tx =sin

, где

11 ≤≤− t

. Из уравнения

0132

=+− tt получаем корни

=t ,

которые удовлетворяют условию

11 ≤≤− t .

а) Если

1sin =x

, то

0cos =x

и из второго урав-

нения системы имеем

0=y . Это значение не

удовлетворяет условию

0>y .

б) Пусть

sin =x , тогда из тождества

1cossin

=+ xx получаем

cos =x и

cos −=x

. Отсюда

или

−=y

(не

удовлетворяет условию

0>y ).

Из уравнения

sin =x имеем

.,2

Znnx ∈+=

Таким образом, исходная система имеет реше-

ния

,,2

=∈+= yZnnx

Ответ:

,,2

=∈+= yZnnx

Критерии:

Содержание критерия Баллы

Обоснованно получен вер-

ный ответ.

Получен ответ, возможно,

неверный, но только из-за

того, что в решении не уч-

тено, что знаменатель дроби

существует и отличен от

нуля.

Решение не соответствует

ни одному из критериев, пе-

речисленных выше.

34. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−=

−

cos

1sin3sin2

Ответ:

,,2

−=∈+−= yZnnx

35. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−

+⋅−

cos

)21(log

84616

sinsin

Ответ:

,,2

−=∈+= yZnnx

36. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

+⋅−

sin

)21(log

2791281

coscos

Ответ:

,,2

=∈+= yZnnx

37. Решите систему уравнений

⎩

⎨

⎧

=−

1cossin

1sinsin

Ответ:

.,,

)1(;

)1(

ZkZnkn

∈∈

⎟

⎠

⎞

⎜

⎝

⎛

+⋅−+⋅−

38. Решите систему уравнений

(

)

⎪

⎩

⎪

⎨

⎧

=−−

yxx

sin

0cos352

Ответ: ;,

;)1( Znn

∈

⎟

⎠

⎞

⎜

⎝

⎛

+−

.,2

;

Zkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

+−−

39. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

−=+

3sinsin

)cos(

Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

++ kn

.,,2

ZkZnkn ∈∈

⎟

⎠

⎞

⎜

⎝

⎛

40. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

=−

1sinsin

Решение. Рассмотрим два случая, связанные с

раскрытием модуля.

1. Если

=− yx , то

−= xy . Первое урав-

нение системы примет вид

sinsin =

⎟

⎠

⎞

⎜

⎝

⎛

−+

sincos

cossinsin =⋅−⋅+

xxx

;1cos

sin

sin =−− xxx

;1cos

sin

=− xx

sin =

⎟

⎠

⎞

⎜

⎝

⎛

−

.,2

Znnx ∈+=

Отсюда

.,2

Znny ∈+=

2. Если

−=− yx , то

+= xy . Первое

уравнение системы примет вид

sinsin =

⎟

⎠

⎞

⎜

⎝

⎛

sincos

cossinsin =⋅+⋅+

xxx

;1cos

sin

sin =+− xxx

;1cos

sin

=+ xx

sin =

⎟

⎠

⎞

⎜

⎝

⎛

.,2

Zkkx ∈+=

Отсюда

.,2

Zkky ∈+=

Ответ:

;,2

Znnn ∈

⎟

⎠

⎞

⎜

⎝

⎛

.,2

Zkkk ∈

⎟

⎠

⎞

⎜

⎝

⎛

Критерии:

Содержание критерия Баллы

Обоснованно получен вер-

ный ответ.

Получен ответ, но решение

не верно из-за ошибки в

формулах или значениях

тригонометрических функ-

ций, из-за неверной записи

ответа.

Решение не соответствует

ни одному из критериев, пе-

речисленных выше.

41. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

≤≤

sincos

2sinsin

Ответ:

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

;0;

;

πππ

42. Решите систему уравнений

⎪

⎩

⎪

⎨

⎧

sin

Ответ:

;

Znnn ∈

⎟

⎠

⎞

⎜

⎝

⎛

−+

Задания С 2

РАССТОЯНИЯ И УГЛЫ

В ПРОСТРАНСТВЕ

Методы решения задач

1. Поэтапно-вычислительный метод

Координатный метод

Координатно-векторный метод

Векторный метод

Метод объемов

Метод ключевых задач

Ключевые задачи

1. Координаты точки

()

zyxM ;; , делящей отре-

зок

между точками

()

1111

;; zyxM

()

2222

;; zyxM в отношении MM

MM ,

определяются формулами

2. Найти угол между диагоналями смежных гра-

ней куба.

3. Найти угол между диагональю куба и скре-

щивающейся с ней диагональю грани.

4. Найти угол между диагональю куба и плоско-

стью, проведенной через концы трех ребер куба,

выходящих из той же вершины, что и диагональ.

5. В кубе

1111

DCBABCDA диагональ

BD пер-

пендикулярна плоскостям

CAB

DCA

и де-

лится ими на три равные части.

6. Отрезки, соединяющие середины противоле-

жащих ребер тетраэдра, пересекаются в одной

точке и делятся этой точкой пополам.

7. В правильной треугольной пирамиде скрещи-

вающиеся ребра перпендикулярны.

8. Отрезок, соединяющий середины скрещи-

вающихся ребер правильного тетраэдра, являет-

ся их общим перпендикуляром и имеет длину

2а

, где а – длина ребра.

9. Любое сечение треугольной пирамиды плос-

костью, параллельной ее скрещивающимся реб-

рам, является параллелограммом.

10. Любое сечение правильной треугольной пи-

рамиды плоскостью, параллельной ее скрещи-

вающимся ребрам, есть прямоугольник.

1. Расстояние между двумя точками

Расстояние между точками А и В можно вы-

числить:

1) как длину отрезка АВ, если отрезок АВ удает-

ся включить в некоторый треугольник в качест-

ве одной из его сторон;

2) по формуле

()( )( )( )

; zzyyxxBA −+−+−=

, где

()

111

;; zyxA ,

()

222

;; zyxB ;

3) по формуле

ABAB = .

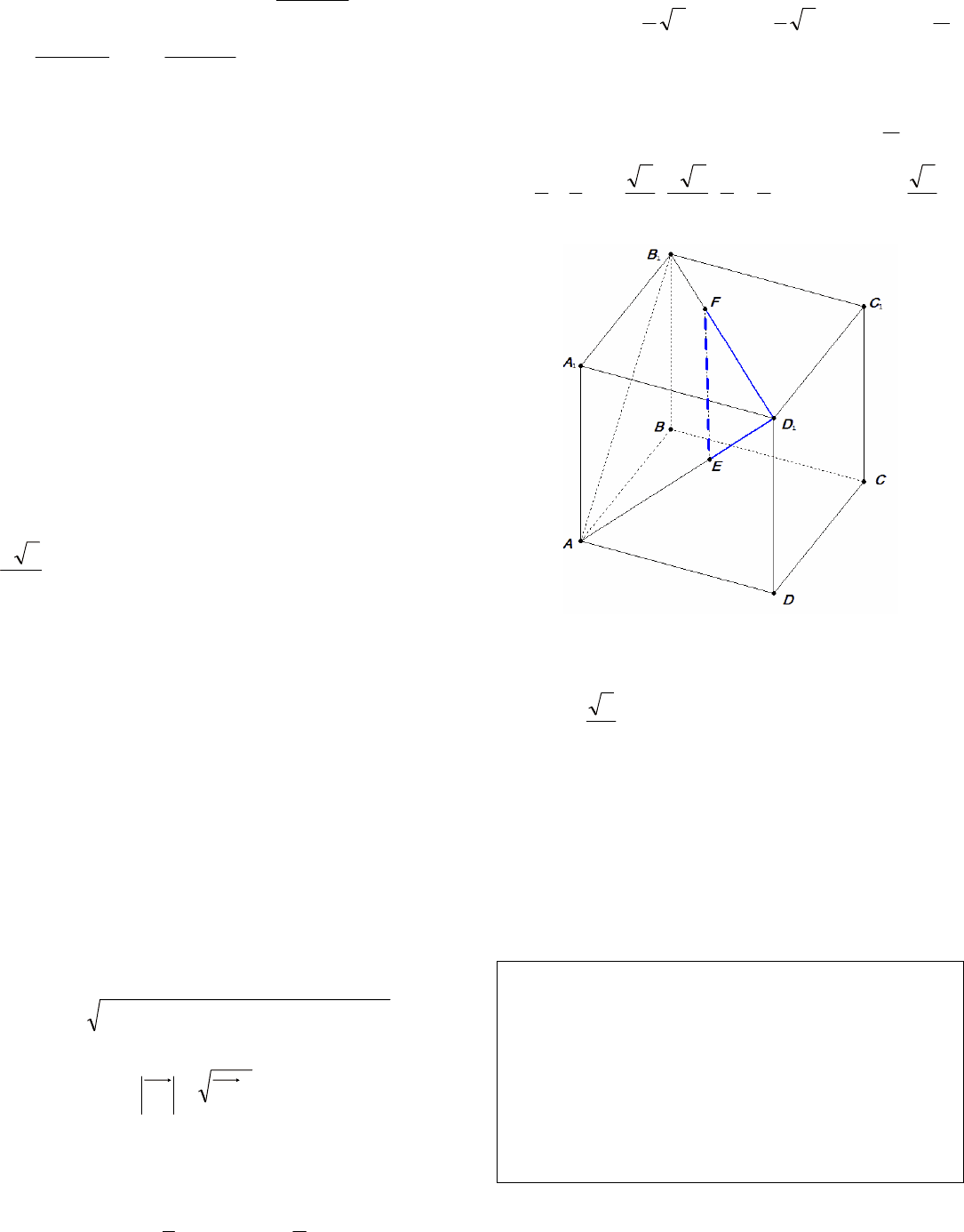
Пример 1. В единичном кубе

1111

DCBABCDA

на

диагоналях граней

AD и

BD взяты точки Е и

F так, что

ADED = ,

111

BDFD = . Найдите

длину отрезка EF.

Решение. Длину отрезка EF найдем по теореме

косинусов из треугольника

EFD

(рис. 1), в ко-

тором

=FD , 2

=ED ,

=∠ EFD

(треугольник

DAB является равносторонним).

Имеем

=⋅⋅−+=

cos2

FDEDFDEDEF

=⋅⋅⋅−+= , откуда

=EF .

Рис. 1

Ответ:

1. (П) Ребра правильной четырехугольной приз-

мы равны 1, 4 и 4. Найдите расстояние от вер-

шины до центра основания призмы, не содер-

жащего эту вершину.

Ответ: 3.

2. Расстояние от точки до прямой

Расстояние от точки до прямой, не содержа-

щей эту точку, есть длина отрезка перпендику-

ляра, проведенного из этой точки на прямую.

Расстояние между двумя параллельными пря-

мыми равно длине отрезка их общего перпенди-

куляра.

Расстояние между двумя параллельными пря-

мыми равно расстоянию от любой точки одной

из этих прямых до другой прямой.

Расстояние от точки до прямой можно вы-

числить:

1) как длину отрезка перпендикуляра, если уда-

ется включить этот отрезок в некоторый тре-

угольник в качестве одной из высот;

2) используя векторный метод;

3) используя координатно-векторный метод.

Пример 2. При условиях примера 1 найдите

расстояние от точки

D до прямой EF.

Решение. Пусть h – длина высоты треугольника

EFD

, опущенной из точки

D . Найдем h, ис-

пользуя метод площадей. Площадь треугольни-

ка

EFD

равна =∠⋅⋅ EFDEDFD

111

sin

=⋅⋅⋅= . С другой стороны

площадь треугольника

EFD

равна

hhFE

=⋅ . Из уравнения

= нахо-

дим искомое расстояние

=h .

Замечание. Можно заметить, что выполняется

равенство

FDEDFE =+ , то есть тре-

угольник

EFD

прямоугольный и длина отрезка

является искомым расстоянием.

Ответ:

1. (П) В единичном кубе

1111

DCBABCDA найди-

те расстояние от точки А до прямой:

DB ; б) СА

; в)

BD .

Ответ: а)

; б)

; в)

2. (П) В правильной треугольной призме

111

CBABCA , все ребра которой равны 1, найдите

расстояние от точки А до прямой

ВС

Ответ:

3. (П) В правильной шестиугольной призме

111111

FEDCBABCDEFA

, все ребра которой равны

1, найдите расстояние от точки А до прямой:

а) DЕ; б)

ED ; в)

CB ; г)

BE ; д)

BC ; е)

CE ;

ж)

CF ; з)

CB .

Ответ: а)

3; б) 2; в)

; г)

; д)

;

е)

; ж)

; з)

4. (П) Основание прямой призмы

1111

DCBABCDA

− ромб ABCD, в котором

,10

АВ .76=АС Боковое ребро

АА равно

.213

Найдите расстояние от вершины В до

прямой

АС

Ответ: 8.

3. Расстояние от точки до плоскости

• Расстояние от точки до плоскости, не со-

держащей эту точку, есть длина отрезка перпен-

дикуляра, опущенного из этой точки на плос-

кость.

• Расстояние между прямой и параллельной ей

плоскостью равно длине их общего перпенди-

куляра.

• Расстояние между прямой и параллельной ей

плоскостью равно расстоянию от любой точки

этой прямой до плоскости.

• Расстояние между двумя параллельными

плоскостями равно длине их общего перпенди-

куляра.

• Расстояние между двумя параллельными

плоскостями равно расстоянию между точкой

одной из этих плоскостей и другой плоскостью.

Расстояние от точки М до плоскости

1) равно расстоянию до плоскости

от произ-

вольной точки Р, лежащей на прямой l, которая

проходит через точку М и параллельна плоско-

сти

;

2) равно расстоянию до плоскости

от произ-

вольной точки Р, лежащей на плоскости

, ко-

торая проходит через точку М и параллельна

плоскости

;

3) вычисляется по формуле

ρρ

= , где

(

)

()

;

M= , ,rOM

rOM

OMM

∩

; в частности,

если

прямая m, проходящая через точку М, пересе-

кает плоскость

в точке О, а точка

М лежит

на прямой m;

4) вычисляется по формуле

()( )

ABC

ABCM

ABCMM

;; ==

ραρ

, где треугольник

АВС расположен на плоскости

, а объем пи-

рамиды АВСМ равен

ABCM

V ;