Кормильцев В.В., Ратушняк А.Н., Петряев В.Е. Методы моделирования геофизических полей

Л е к ц и я 2

НЬЮТОНОВ ПОТЕНЦИАЛ

Рассмотрение целесообразно начать с потенциала притяжения, что

является теоретической основой гравиметрии. Далее будет показано, что и

при вычислении других потенциальных полей производные потенциала

притяжения играют важную роль.

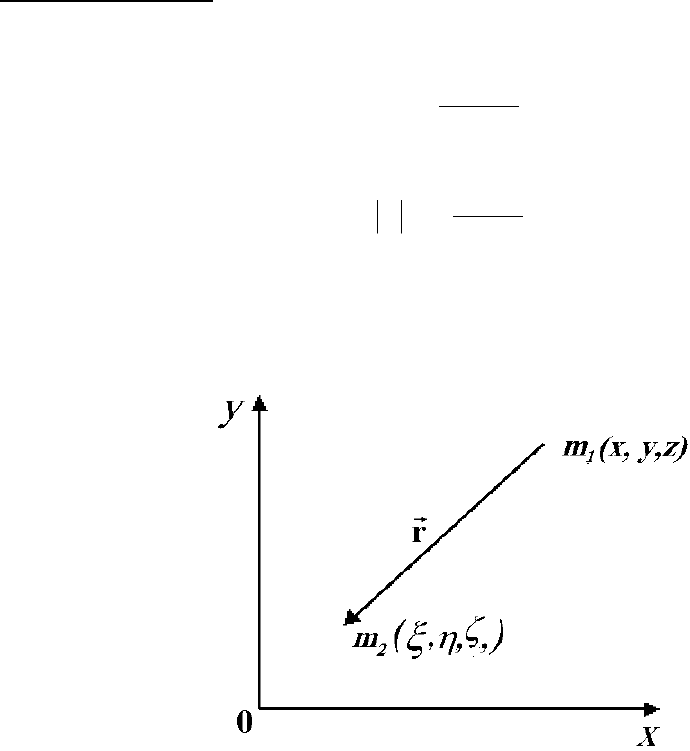
Сила притяжения. По закону Ньютона, сила притяжения между двумя то-

чечными массами m

1

и m

2

, находящимися на расстоянии r друг от друга,

определяется равенством

3

21

r

mm

k

r

f =

,

или для модуля силы

2

21

r

mm

kf =

,

где r=(

ξ

–x)i+(

η

–y)j+(

ζ

–z)k, r

2

=(

ξ

–x)

2

+(

η

–y)

2

+(

ζ

–z)

2

, x, y, z – координаты

массы

m

1

, а

ξ

,

η

,

ζ

– координаты массы m

2

, k – постоянная тяготения,

k=6,67⋅10

-8

см

3

⋅г

-1

⋅с

-2

.

Рис.3

Поскольку 1 см/с

2

=1 Гал, то иначе k=6,67⋅10

-5

мГал⋅см

2

⋅г

-1

=6,67⋅10

-3

мГал⋅м/(г/см

3

)=6,67 мГал⋅км/(г/см

3

). Пусть m

1

<<m

2

. Сила притяжения еди-

ничной массы

m

1

=1, оказываемая какой-либо неточечной массой, распре-

деленной в объеме

V

10

∫

=

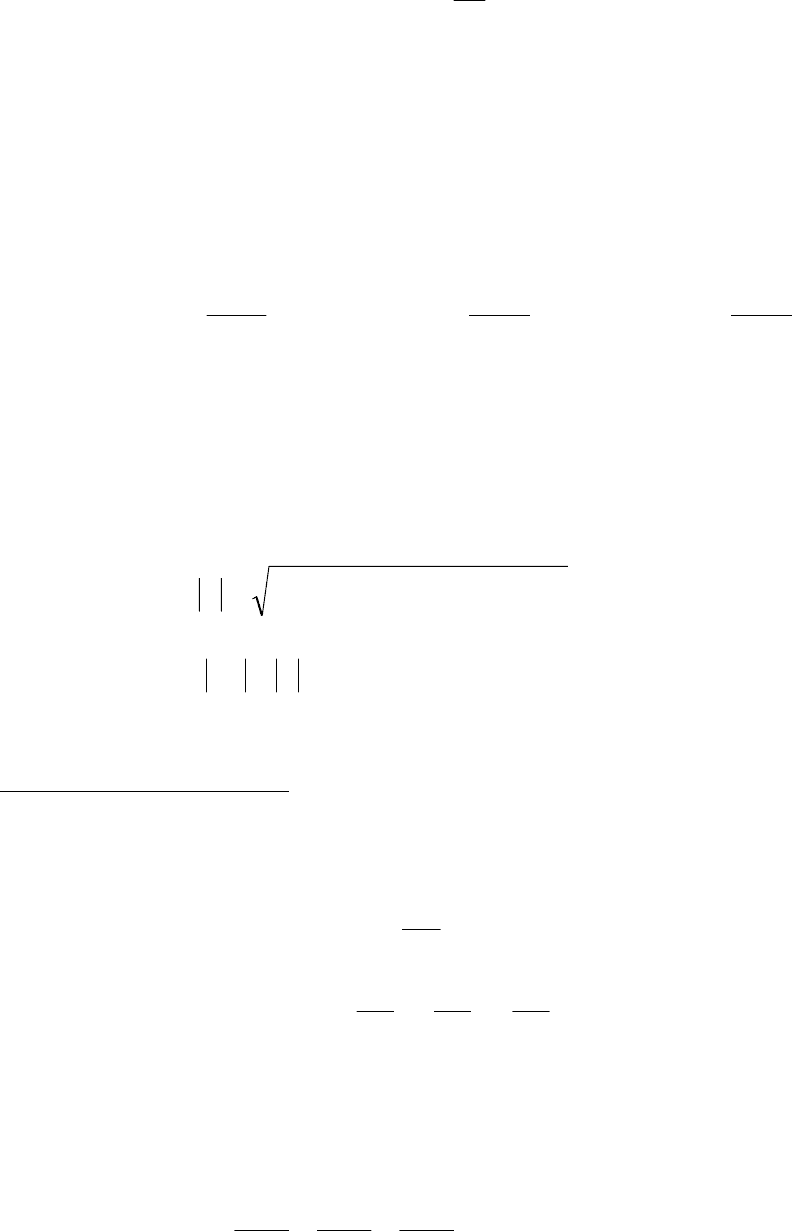
V

dm

r

k

3

r

F

.

Поскольку при действии постоянной силы F масса

m

1

приобретает равно-

ускоренное движение f=

m

1

F=m

1

g, то величина F численно равна ускоре-

нию g. Если интегрирование ведется по всему объему Земли, то g – уско-

рение свободного падения или ускорение силы тяжести или просто сила

тяжести. В декартовой системе при

dm=

σ

dV, где

σ

(

ξ

,

η

,

ζ

) – плотность ве-

щества, заполняющего объем

V

g=F=

g

x

i+g

y

j+g

z

k,

∫

−

=

V

x

dV

r

x

kg

3

ξ

σ

,

∫

−

=

V

y

dV

r

y

kg

3

η

σ

,

∫

−

=

V

z

dV

r

z

kg

3

ζ

σ

.

В частном случае

σ

=const и ее можно вынести за знак интеграла. Вертика-

лью называется такое положение оси

OZ декартовой системы, при котором

g

x

=g

y

≡0. Пусть земная кора содержит аномальный локальный объем с из-

быточной плотностью Δ

σ

, который создает аномалию силы тяжести g

xa

,

g

ya

, g

za

. Тогда модуль силы тяжести будет равен в пренебрежении малостя-

ми второго порядка

zazzazyaxa

ggggggg +≈+++=

222

)(,

а его аномалия

zaza

gggg

=

−= .

Таким образом, реально можно измерить лишь вертикальный компонент

аномалии силы тяжести.

Потенциал притяжения. Составляющие g

x

, g

y

, g

z

представляют частные

производные по координатам x, y, z от функции V, называемой ньютоно-

вым потенциалом или потенциалом притяжения

∫

=

V

r

dV

k

σ

V

,

(1)

kjigradg

xyx ∂

∂

+

∂

+

∂

==

VVV

V.

Потенциал V и его первые производные – однозначные, непрерывные и

конечные функции координат притягиваемой точки. Потенциал V – функ-

ция регулярная, то есть на бесконечности стремится к нулю. В каждой точ-

ке вне притягивающих масс потенциал удовлетворяет уравнению Лапласа

0

2

=Δ=

∂

+

∂

+

∂

V

VVV

zyx

,

(2)

11

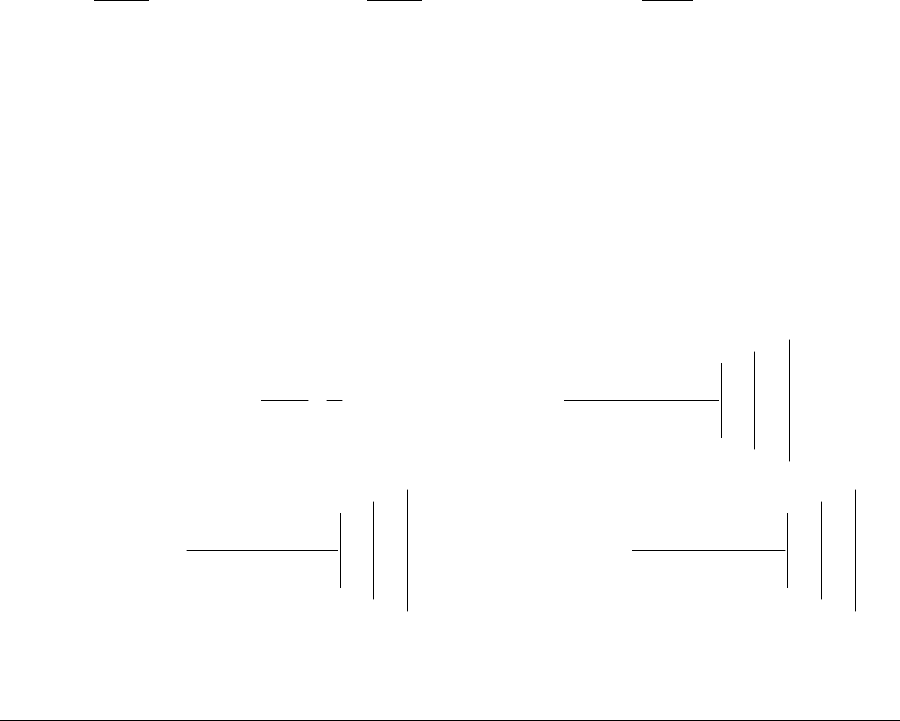
а внутри объема V с притягивающими массами – уравнению Пуассона

σ

π

k

4

−

=

ΔV. (3)

Если (2) очевидно, то доказательство того, что (1) удовлетворяет уравне-

нию (3) является непростой задачей, требующей применения аппарата

обобщенных функций.

Покажем, что (1) удовлетворяет уравнению Лапласа-Пуассона (2, 3) на

примере прямоугольного тела постоянной плотности. Введем обозначения:

xxxx

Gk

x

σ

==

∂

V

2

,

yyyy

Gk

y

σ

==

∂

V

2

,

zzzz

GkV

z

V

σ

==

∂

2

,

где G

xx

, G

yy

, G

zz

– производные от координатного множителя в выражении

(1).Тогда

⎩

⎨

⎧

−

=++

внутри. 4

вне 0

π

zzyyxx

GGG

Для параллелепипеда

()()

()

2

1

2

1

2

1

2

1

2

1

2

1

2

ζ

η

ξ

η

ζ

ξ

ηζ

ζηξ

rx

yz

arctgddd

r

x

G

xx

−

−−

−=

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∫∫∫

,

()()

()

2

1

2

1

2

1

ζ

η

ξ

η

ξζ

ry

xz

arctgG

yy

−

−−

−=

,

()()

()

2

1

2

1

2

1

ζ

η

ξ

ζ

ηξ

rz

yx

arctgG

zz

−

−−

−=

.

При подстановке пределов получаются очень громоздкие выражения, по-

этому далее будем анализировать двумерный случай.

Потенциал притяжения в двумерном случае (логарифмический потенциал).

Рассмотрим двумерный случай. Для того, чтобы перейти к двумерному

случаю проинтегрируем ускорение силы тяжести по

η. К интегрированию

g

z

вместо V прибегают для того, чтобы избежать расходимостей, характер-

ных для логарифмического потенциала.

Итак,

12

() ()()

()()

()

()()

()()() ()()()

()

()()

()

()()

∫∫

∫∫∫

−+−

−

−=

⎥

⎦

⎤

⎢

⎣

⎡

+

−+−

−

−=

⎥

⎦

⎤

⎢

⎣

⎡

−+++−

−−

−

−+−+−

−

×

−+−

−

−=

⋅−+−

−−

−=

−

−=

=

−=

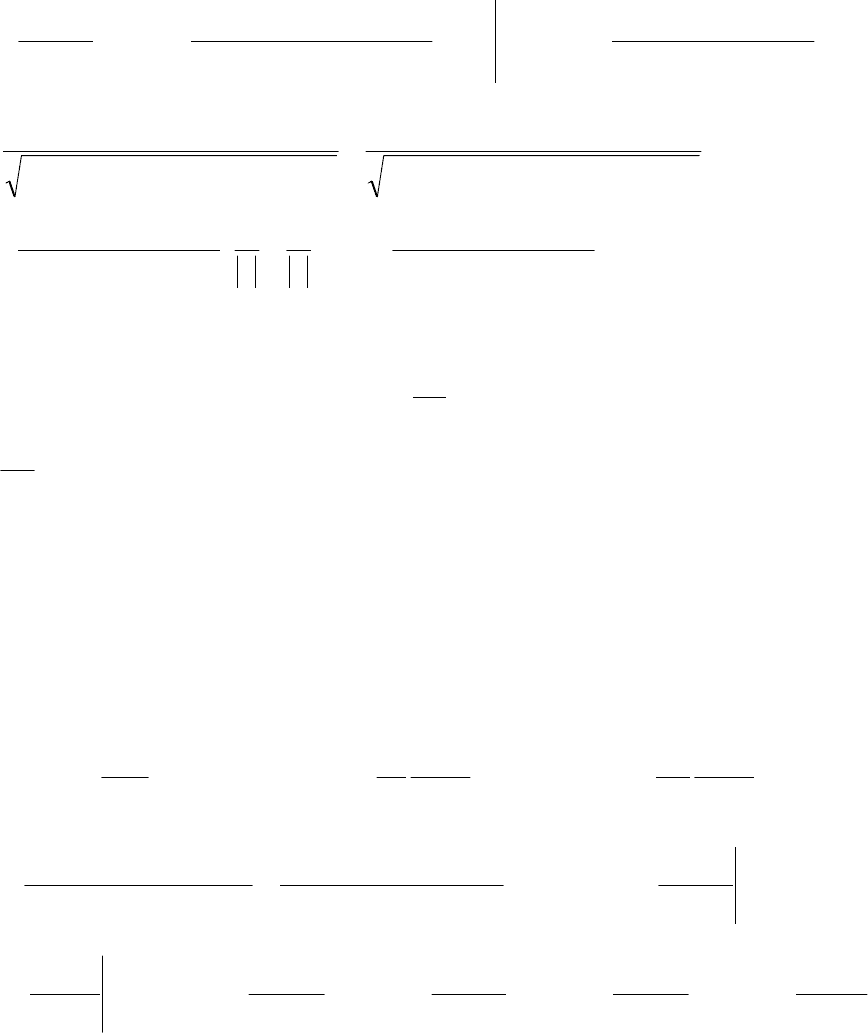
SS

S

a

SV

z

zx

ddz

zx

ddz

dd

zayx

ya

zayx

ya

zx

z

dd

rzx

yz

dV

r

z

G

2222

222222

22223

2

ζξ

ζξζ

η

ζξ

ζξζ

ζξ

ζξζξ

ζξ

ζ

ζξ

ηζζ

η

Теперь можно ввести потенциал

U

g

rad

g

= ,

k

U

σ

gradG = ,

∫∫

−=−=

SS

dSdS

g

U

2

lnln2

ρρ

σ

,

ρ

2

=(x–

ξ

)

2

+(z–

ζ

)

2

.

В двумерном случае уравнение Пуассона примет вид

⎩

⎨

⎧

−

=+

внутри 4

вне 0

π

zzxx

GG

.

Здесь вычисления менее громоздки, поэтому проверим, что дают инте-

гральные формулы для бесконечного бруса прямоугольного сече-

ния:

()

()()

()

()()

1

2

1

2

1

2

22

1

22

2

222

2

22222

22

22)(ln2

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

ξ

ζ

ξ

ζ

ξ

ζ

ξ

ζ

ξ

ζ

ξ

ζ

ζξ

ξ

ζξ

ξ

ζξ

ξ

ζξ

ξ

ζξ

ζ

ξ

ζ

ξ

ζ

ξ

ζ

−

+

−

=

−

=

⎥

⎦

⎤

⎢

⎣

⎡

−+−

−

−+−

−

−=

=

−

∂

−=

−

∂

=

∂

=−

∫

∫∫∫∫∫∫

x

z

arctg

x

z

arctg

x

z

arctg

x

z

arctg

x

z

arctg

x

z

arctgd

zx

x

zx

x

dd

r

x

dd

r

x

ddr

x

G

xx

Поместим центр прямоугольника в начало координат и обозначим

ζ

2,1

=±m,

ξ

2,1

=±n. Воспользуемся формулами приведения тригонометриче-

ских функций (Рис.4).

13

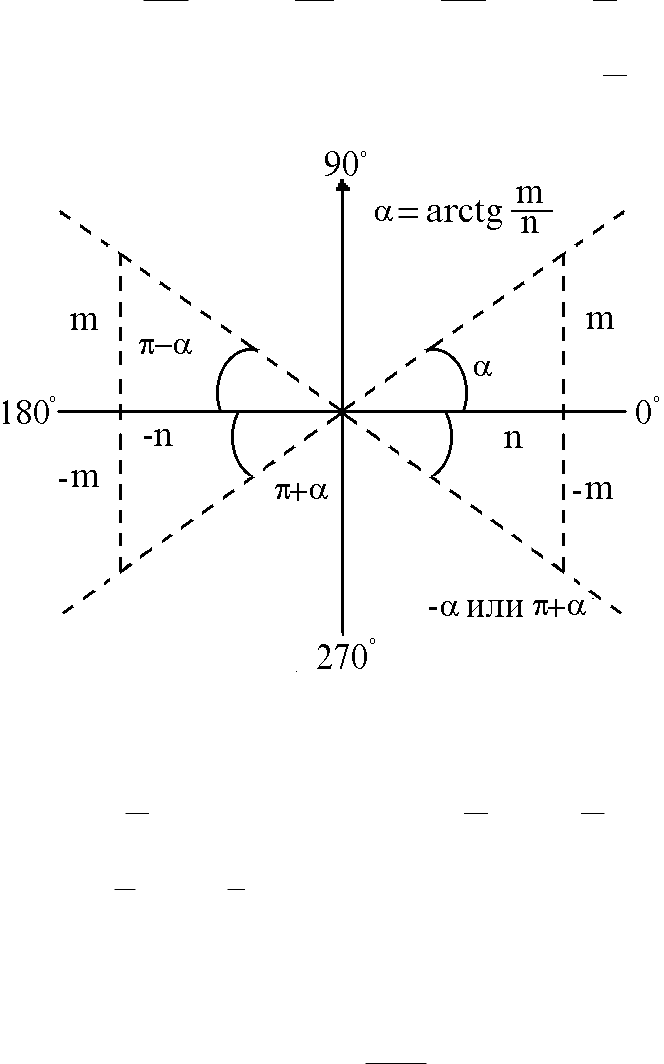
Тогда в центре прямоугольника

()()()

n

m

arctg

n

m

arctg

n

m

arctg

n

m

arctg

n

m

arctgG

xx

882222

2222

==+−−−−+=

=+

−

=−

ααααπαπ

Рис.4

Соответственно,

m

n

arctgG

zz

8=− и

()

π

48 =

⎟

⎠

⎞

⎜

⎝

⎛

+=+−

m

n

arctg

n

m

arctgGG

xxzz

,

поскольку

x

arctgarctgx

1

2

−=

π

.

При вычислении аномалии силы тяжести g

zа

нет проблем, задача сводится

к простому интегрированию выражения g

z,

в котором вместо плотности

σ

подставлена избыточная плотность или ее дефицит

±Δ

σ

()

∑

∫

−

Δ=

n

V

nnz

n

dV

r

z

kzyxg

3

,,

ζ

σ

.

Если

Δ

σ

действительно зависит от координат, объем разбивают на элемен-

тарные объемы, в пределах которых плотность постоянна и выносят ее за

знак каждого отдельного интеграла

14

В двумерном случае

() ( )

∫

−

Δ=

n

V

z

dS

r

z

kzxg

2

,2,

ζ

ζξσ

.

Гравитационное поле по своей структуре является наиболее простым из

потенциальных полей. Добавление какой-либо массы (гравитирующего

объема) не изменяет величины и действия прежних масс. Это обстоятель-

ство и выражают две последние формулы. Остальные потенциальные поля

являются поляризованными. Добавление неоднородности вызывает пере-

распределение всех вторичных источников. Выражения для напряженно-

сти (силы) оказываются более сложными.

Ньютонов потенциал играет важнейшую роль при вычислении дру-

гих потенциальных полей, поскольку, как будет показано далее, его произ-

водные являются компонентами функции Грина в этих задачах.

Вопросы для самопроверки

1.Сила и потенциал притяжения.

2. Потенциал притяжения и уравнение Лапласа – Пуассона.

3. Логарифмический потенциал.

15

Л е к ц и я 3

ОБЪЕМНЫЕ ВЕКТОРНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ПРИ

МОДЕЛИРОВАНИИ ПОТЕНЦИАЛЬНЫХ ПОЛЕЙ.

Напомним некоторые формулы векторного анализа:

,)()( agrad+divaadiv

⋅

=

FFF

(1)

⎪

⎭

⎪

⎬

⎫

∫

=⋅

∫

=

∫

=⋅

∫

=

∫

.(

(

dsNdl)dsdiv

dsGds)dVdiv

L

n

LS

S

n

SV

nNN

nGG

теорема Гаусса, (2)

где Fи G - трехкомпонентные векторы. В частности, в декартовой системе

координат:

kjiF

zyx

+F+FF

=

,

ζ

η

ξ

ddddV

⋅

⋅=

,

kjiG

ζηξ

+G+GG

=

,

S

- поверхность, - нормаль к поверхности,

n

N

- двухкомпонентный вектор,

kiN

ζξ

+NN

=

,

S

- площадь сечения, - контур, - нормаль к контуру. L n

,

z

a

+

y

a

+

x

a

a kjigrad

∂

=

.

z

F

+

y

F

+

x

F

div

z

y

x

∂

=F

Потенциал двух сближенных точечных источников или полюсов имеет вид

1

44 r

Q

r

Q

U

ππ

−=

,

222

)()()(

ζηξ

−+−+−= zyxr

,

222

1

)()()(

ζζηηξξ

dzdydxr −−+−−+−−=

.

Воспользовавшись разложением по малому параметру, получим

3

4

r

Q

U

π

rdl

⋅

−=

,

k

j

idl

ζ

η

ξ

ddd

+

=

,

()

(

)

(

)

kjir

ζηξ

−−−= z+y+x

.

16

Отсюда потенциал диполя имеет вид

() ()

,rrU

MA

/1

4

1

/1

4

1

gradPgradP ⋅=⋅−=

ππ

где

P=Qdl – вектор поляризации, направленный от отрицательного полюса

диполя к положительному, Полный вывод этого выражения предоставляем

читателю. Расстояние

r

можно дифференцировать по тем и другим коор-

динатам, т.е. по обоим концам вектора

r в точках

),,(),,,(

ζ

η

ξ

MzyxA

, при

этом

()

,

r

A

3

/1

r

grad −=

()

,/1

3

r

M

r

grad =

т.е. производные, отличаются только знаком.

Пусть

P=pdV, где dV – элементарный объем, p– вектор поляризации

единицы объема, в общем случае зависящий от координат. Тогда для тела

объемом

V аномальный потенциал, возникающий вследствие его поляри-

зации, равен

() ()

dVrU

M

V

/1,,

4

1

gradp

∫

=

ζηξ

π

. (3)

Скалярное произведение, стоящее под знаком интеграла, может быть

представлено согласно формуле (1) в следующем виде:

() ()

./1 r/div

r

+div

r

div

r p

pp

gradp =−=⋅

Последнее равенство справедливо, если поляризация однородна и

. Воспользовавшись формулой Гаусса (2), имеем

div p = 0

()

.

4

1

4

1

/1

4

1

∫∫

==

∫

⋅=

SVV

M

r

dV

n

p dV

r

div dVrU

πππ

p

gradp

(4)

В частности, если , где - намагниченность, то магнитный

потенциал однородно намагниченного тела, ограниченного поверхностью

nn

Ip =

I

S

, имеет известный вид:

.

4

1

∫

−=

S

n

ds

r

I

U

π

(5)

При этом напряженность магнитного поля равна:

.

4

1

4

1

3

∫∫

=−=−=

S

n

S

n

AA

ds

r

I

ds

r

I

U

r

gradgradH

ππ

(6)

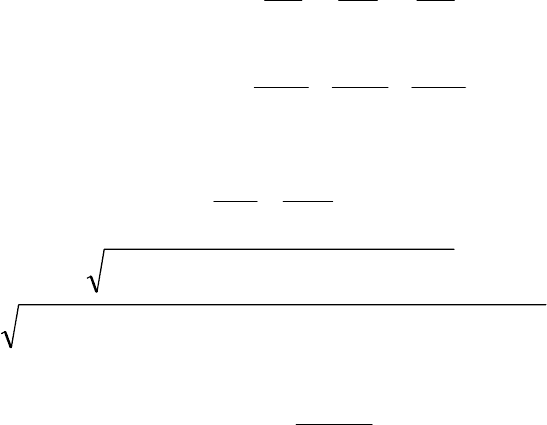
Рассмотрим объект в виде прямоугольной пластины (рис.5), намаг-

ниченной вдоль короткого вертикального ребра

)kI

z

I

=

(

.

17

Рис.5

В этом случае для однородной намагниченности, например, вертикальная

составляющая равна:

() ()

∫∫

⋅

−

∫∫

−⋅

−

=

2

1

2

1

3

1

2

1

2

1

3

2

4

1

4

1

ξ

η

ηξ

ζ

π

ξ

η

ηξ

ζ

π

dd

r

zI

dd

r

zI

zz

z

H

(

)

(

)

(

)

2

1

22

2

1

ζηξ

−+−−= zy+xr

,

(

)

(

)

(

)

2

22

2

ζηξ

−+−−= zy+xr

.

Однородная намагниченность

HI κ

=

возникает в однородном на-

магничивающем поле . Однако даже в однородном поле объект,

обладающий высокой магнитной восприимчивостью

κ, намагничивается

неоднородно. На рис.3 видно, что размагничивающее поле почти вдвое

меньше для крайнего элемента, чем для остальных. Краевые части тела на-

магничиваются сильнее, и намагниченность перестает быть однородной у

однородного по свойствам объекта в однородном намагничивающем поле.

Исключение составляют безграничная пластина и тела, ограниченные по-

верхностями второго порядка.

HH=

0

Для сильно поляризованных тел (хороших магнетиков, высоко элек-

тропроводных руд и других контрастных с вмещающей средой образова-

ний) необходимо искать другие способы вычисления аномального потен-

циала и напряженности вместо выражений (4-6).

18

Выражение (3) имеет самый общий характер. Необходимо лишь най-

ти связь между вектором поляризации

и суммарным полем, состоящим

из первичного поля и поля всех элементарных объемов. Рассмотрим эту

проблему на примере электрического поля постоянного тока.

P

Как известно,

nnne

PEE

=

−

,

ne

E

- нормальная составляющая напряженности электрического поля с

наружной (external) стороны включения,

- с внутренней стороны.

n

E

На границе непрерывна нормальная составляющая плотности полно-

го тока

nne

ii =

,

cnncnenee

iEiE

+

=

+

σ

,

где и - нормальные составляющие плотности стороннего тока на

внешней и внутренней сторонах границы включения. Отсюда

c

i

cn

i

e

cec

n

e

ne

ii

EE

σσ

σ

−

+=

и

e

сeс

n

e

n

ii

EP

σσ

σ

−

+

⎟

⎠

⎞

⎜

⎝

⎛

−= 1

(7)

Если нормальная составляющая вектора поляризации дана выраже-

нием (7), то весь вектор равен

e

cec

e

σσ

σ

ii

EP

−

+

⎟

⎠

⎞

⎜

⎝

⎛

−= 1

Подставляя (8) в (3) и добавляя потенциал первичного поля ,

имеем во всем пространстве

0

U

()

dVrUU

M

V

e

cec

e

/11

4

1

0

grad

ii

E

∫

⎥

⎦

⎤

⎢

⎣

⎡

−

+

⎟

⎠

⎞

⎜

⎝

⎛

−+=

σσ

σ

π

, (9)

Откуда

dV

r

V

e

сeс

e

A

3

0

1

4

1 r

ii

∫

⎥

⎦

⎤

⎢

⎣

⎡

−

+

⎟

⎠

⎞

⎜

⎝

⎛

−−=

σσ

σ

π

EgradEE

, (10)

Более строгий вывод уравнения (10) с использованием формулы

Грина приведен в статье [7].

Выражение (10) для внешних точек является интегральной формулой

для вычисления внешней напряженности по значениям внутренней. Для

19

Кормильцев В.В., Ратушняк А.Н., Петряев В.Е. Методы моделирования геофизических полей

Подождите немного. Документ загружается.