Контрольная работа (вариант 8)
Подождите немного. Документ загружается.

Министерства образования и науки Российской Федерации
Уфимский государственный авиационный технический университет
Кафедра общей физики
Контрольная работа №1 по разделам:
«Физические основы механики»,
«Молекулярная физика и термодинамика»
Выполнил: студент гр. ЭМ-107
Факультета заочного отделения УГАТУ,
ул. М.Жукова 11/2 кв. 64
_________________Кордяк А.М.
(подпись)
Проверил: Афанасьева А.М.
____________________________
(подпись)
____________________________
Дата «___»______________2007
УФА 2007
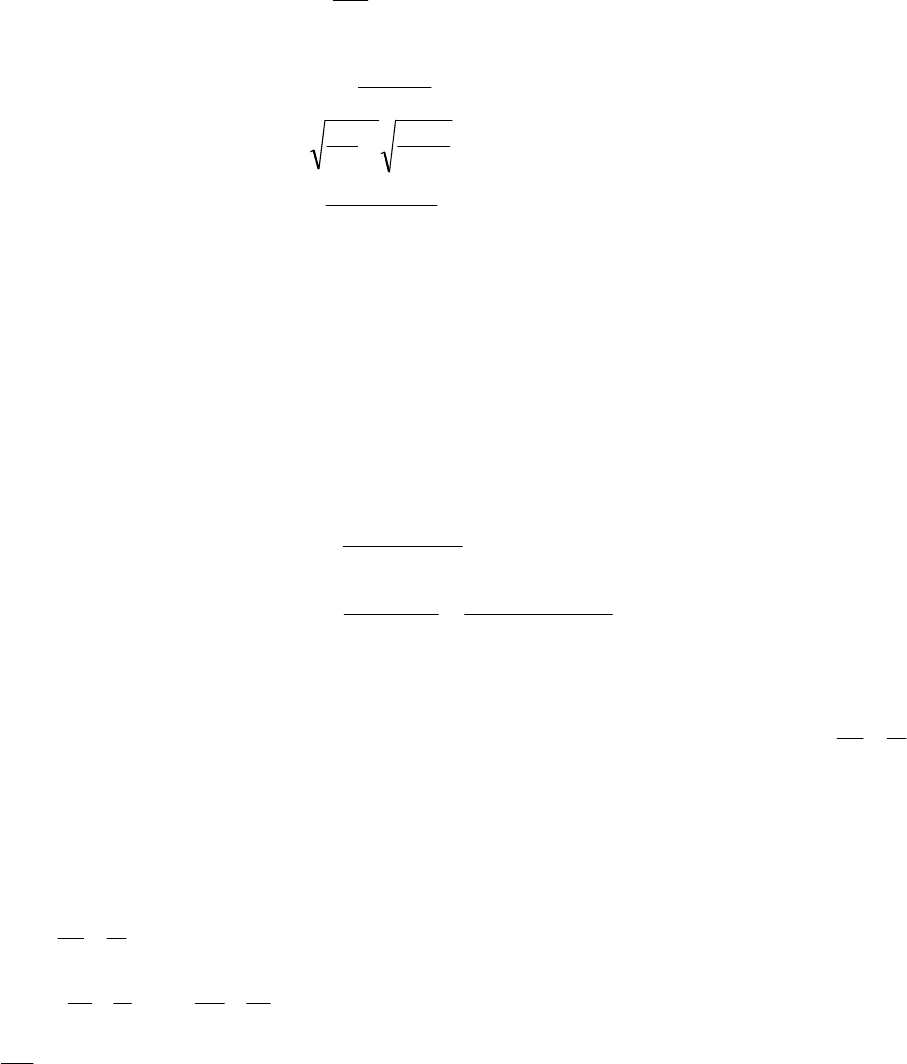
1.8 Тело падает с высоты h=1 км с нулевой начальной скоростью. Пренебрегая
сопротивлением воздуха, определить, какой путь пройдет тело: 1) за первую секунду
своего падения; 2) за последнюю секунду своего падения. Ответ: 1) 4,9м; 2) 132 м.
Дано:
h= 1 км = 1000 м
v
0
=0
R
B
=0
Найти:
S
1
=?
S
посл.
=?
Решение:
а= const
,
2
2
0
at
tvS
8,9ga
т.к. R
B
=0
)(9,4
2
1*8,9
1*0
2
1
мS
29,14
8,9
20002
.
a
S
t
общ
)(46,865
2
29,13*8,9
29,13
мS
)(54,13446,8651000
29,13.
мSSS
ПОСЛ
Ответ: S
1
=4,9 м, S
посл.
= 134,54 м
2.8 Снаряд массой m = 5 кг, вылетевший из орудия, в верхней точке траектории
имеет скорость υ = 300 м/с. В этой точке он разорвался на два осколка, причем больший
осколок массой m
1
= 3 кг полетел в обратном направлении со скоростью υ
1
=100Rм/с.
Определить скорость υ
2
второго, меньшего, осколка. Ответ: 900Rм/с.
Дано:
m = 5 кг
v = 300 м/с
m
1
= 3 кг
v
1
= 100 м/с
Найти:
v
2
= ?
Решение:
21
2211
mm
vmvm
U
см
mm
vmmv
v /900
2
100*3300*5
1
11
2
Ответ: v
2
= 900 м/с
2.52 Зависимость потенциальной энергии П тела в центральном силовом поле от
расстояния r до центра поля задается функцией
r
B
r
A
rП
2
)(
АR=R6RмкДж·м
2
,RВ=0,ЗRмДж·м). Определить, при каких значениях r максимальное
значение принимают: 1) потенциальная энергия тела; 2) сила, действующая на
тело. Ответ: 1) r =2А/B = 4см; 2) r = ЗА/В=6см.
Решение:
r
B
r
A
rП
2
)(
;
0
2
)(
23
|
2
|
r
B
r
A
r
B
r
A
rП
r
;
0
2
B
r
A
(из условия экстремума);
2
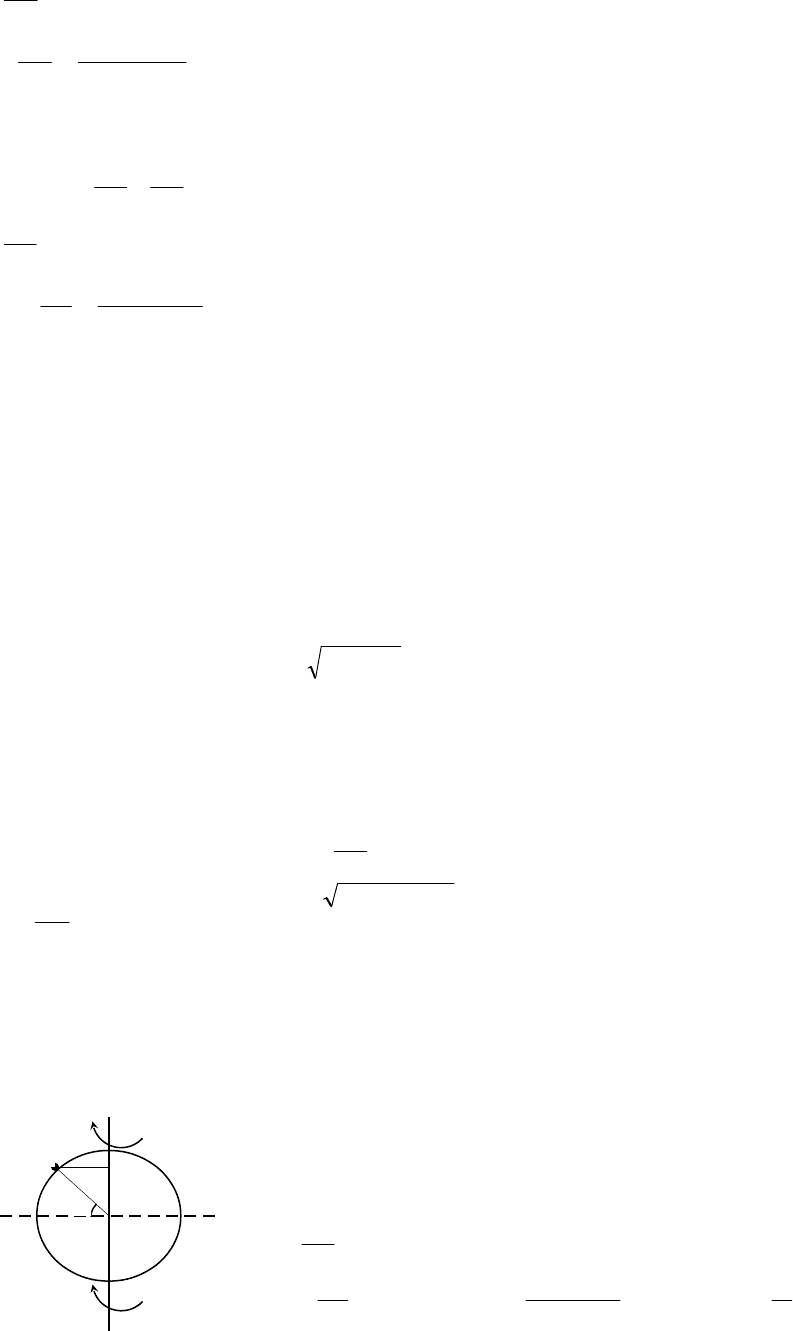
)(410*4
10*3,.0
10*6*22
2
2
3
6
смм
B
A
r
B
r
A
Сила, действующая на тело, принимает максимальное значение при:
0
26
)(
0)(
34
//
//
r
B
r
A
rП
rП
)(610*6
10*3,0
10*6*33
2
6
2
3
6
смм
B
A
r
B
r
A
Ответ: r = 4см; r =6см.
1.24 Зависимость пройденного телом пути по окружности радиусом r=R3 м
задается уравнением s = At
2
+ Bt (A = 0,4 м/с
2
, ВR=R0,1 м/с). Определить для момента
времени t=R1Rс после начала движения ускорения: 1) нормальное; 2) тангенциальное; 3)
полное. Ответ: 1) 0,27 м/с
2
; 2) 0,8 м/с
2
; 3) 0,84 м/с
2
.
Дано:
r= 3 м
s = At
2
+ B
A = 0,4 м/с
2
,
ВR=R0,1 м/с
t=R1Rс
Найти:
a
n
= ?
a
t
=?
a= ?
Решение:
Нормальное
ускорение:
a
т
=
r
V
2
V=S= 2At+B= 2*0,4+0,1=0,9 м/с
Тангенциальное ускорение:
a
r
= V= S = 2A = 2*0,4= 0,8 м/с
2
Полное:
а=
22
rn
aa
2
/27,0
3
9,0
смa
n
222
/844,08,027,0 смa
Ответ: a
n
= 0,27 м/с
2
; a
r
= 0,8 м/с
2
; а = 0,844 м/с
2
1.30 Найти линейную скорость υ вращения точек земной поверхности на широте Санкт-
Петербурга (φR=R60
о
). Ответ: 231 м/с.
Решение:
Линейная скорость вращения выражается через угловую w
V = wr,
где r = Rcosφ – радиус вращения
R – радиус земли
V= Rwcosφ
;
2
T
w
Т = 1 сут. = 24 часа = 86R400 с –период вращения Земли;
с
м
T
RV 23160cos*
10*64,8
2
*10*4,6cos
2
0
4
6
Ответ: V = 231 м/с.
3
A
R
φ
V

3.8 К ободу однородного сплошного диска массой m = 10 кг, насажанного на ось,
приложена постоянная касательная сила F=R30RH. Определить кинетическую энергию
диска через время t=R4Rс после начала действия силы. Ответ: 1,44 кДж.
Дано:
F = 30 H
t = 4 c
m = 10 кг
Найти:
Е
К
= ?
Решение:
Согласно
2-му
закону
Ньютона
для
вращатель
ного
движения:
EJМ
М
- сумма моментов всех сил, действующих на всё тело
Е
– угловое ускорение тела
2
2
1
mRJ
- момент инерции диска
FRM
R – радиус диска
R
a
E
Имеем:
EmRFR
2
2
1
R
a
mRFR
2
2
1
m
F
amaF
2
2
1
- тангенциальное ускорение точек на ободе диска
Скорость точек на ободе:
V= a
τ
t
Кинетическая энергия диска:
кДжДж
m
tF
m
tF
t
m
F
m
tam
R
ta
mR
R
V
J
Jw
E
k
44,11440
10
4*30
*
4
*4
4
*
2
4
*
2
2
1
22
22
2222
2
2
2
2
2
2
2
2
Дж
с
мкг
кг
с
с
мкг
кг
сН
m
tF
E
K
2
2
2
2
2
22
22
*
*
*
**
Ответ: Е
К
= 1,44 кДж
3.24 Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением
ε = 0,4 рад/с
2
. Определить кинетическую энергию маховика через время t
2
= 25 с после
начала движения, если через t
1R
=R10 с после начала движения момент импульса L
1
маховика составлял 60кг·м
2
/с. Ответ: 1) Е
кR
=R75RДж.
4

Дано:
Е = 0,4 с
-2
t
2
= 25c
t
1
= 10 c
L
1
= 60 кгм
2
/с
Найти:
Е
к2
= ?
Решение:
L
1
= Jw
1
w
1
= Et
1
L
1
= JEt
1
1
1
Et
L
J
2
2
2
Jw
E
кг
w
2
= Et
2
Дж
EtL
Et
Et
L
E
K
750
10*2
25*4,0*60
22
*
2
2
21
2
2
1
1
2
Дж
с
мкг
с
с
с
с
мкг
t
tEL
E
K
2
2
2
2
2
*
1*
Ответ: Е
К2
= 750 Дж

4.8 Определить собственную длину стержня, если в лабораторной системе его скорость υ
= 0,6 с, длина l = 1,5 м и угол между ним и направлением движения
=30°. Ответ: 1,79 м.
Решение
Пусть проекция стержня на ось Х в лабораторной системе
l
X
. Тогда собственная проекция стержня на ось х – L
0X
По теории относительности
2
0
1
XX
ll
В тоже время l
X
= l*cosV
2
0
1*cos*
x
lVl
624,1
6,01
30cos*5,1
1
cos*
2
0
2
0
Vl
l
X
Проекция на ось у не зависит от скорости
l
y
= l
0y
= l*sinV = 1,5*sin30
0
= 0,75 м
Поэтому угол между стержнем собственной длины и направление покоя будет:
0
0
79,24462,0
624,1
75,0
x
y
l
l
tg
Тогда собственная длина стержня:
м
l
l
x
79,1
79,24cos
624,1
cos
0
0
0
Ответ: l
0
= 1,79
5.8 Тело массой m= 10 г совершает гармонические колебания по закону x = 0,1 cos (4πt +
π/4) м. Определить максимальные значения: 1) возвращающей силы; 2) кинетической
энергии. Ответ:1) 0,158 Н; 2) 7,89 мДж.
Решение:
x = 0,1 cos (4πt + π/4) м.
)
4
4cos(*6,1)
4
4cos(4*4,0
)
4
4sin(4,0)
4
4sin(*1,0*4
2
ttXVa
ttXV
Максимальное значение возвращающей силы:
F
макс
= m*a
макс
= 0,01*1,6π
2
= 0,158 H
Максимальное значение кинетической энергии:
Дж
mV
E
MAX
K
3
2
2
max
10*89,7
2
)4,0(*01,0
2
Ответ: F
MAX
= 0,158 H
(E
K
)
MAX
= 7,89 мДж
5.17 Если увеличить массу груза, подвешенного к спиральной пружине, на 600Rг, то
период колебаний груза возрастает в 2 раза. Определить массу первоначально
подвешенного груза. Ответ: 0,2Rкг.
Решение:
Пусть m
0
– начальная масса груза. Тогда m
0
+∆m – масса груза после увеличения. Тогда
соответствующие периоды будут:
K
m
Т
0
0
2
K
mm
T
0
1
2
l
V
V
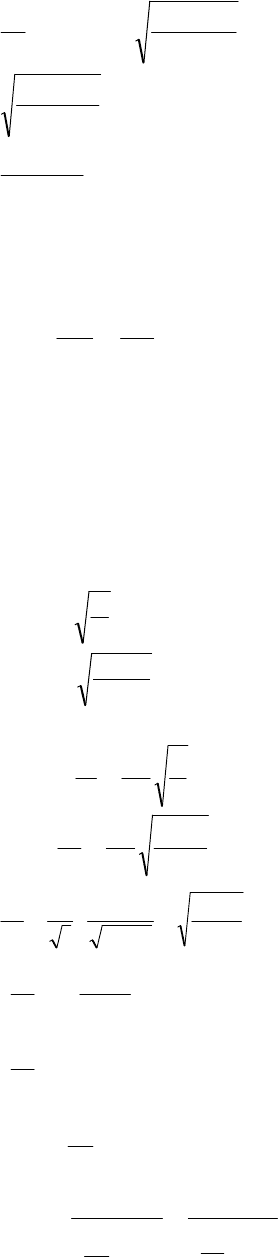
Где К – жесткость пружины;
По условию:
2;2
0
0
0
1
m
mm
тогда
T
T
4
2
0
0
0
0
m
mm
m
mm
кг
m
m
mm
mmm
mmm
2,0
3
6,0
3
3
4
4
0
0
00
00
Ответ: m
0
= 0,2 кг
5.26 Два математических маятника, длины которых отличаются на Δl= 16Rсм, совершают
за одно и то же время один n
1
= 10 колебаний, другой — n
2
= 6 колебаний. Определить
длины маятников l
1
и l
2
. Ответ: l
1
= 9 см, l
2R
=R25Rсм.
Решение:
Пусть l – длина первого маятника;
Тогда периоды колебаний будут:
g
ll
T
g
l
T
2
2
2
1
Пусть за время t первый маятник совершает n
1
= 10 колебаний. Тогда:
ll
gt
T
t
n
l
gt
T
t
n
2
2
2
2
1
1
ll
g
lll
n
n
1
:
1
2
1
lll
n
n
l
ll
n
n
*
2
2
1
2
2
1
м
n
n
l
ll
l
n
n
l
09,0
1
6
10
16,0
1
1
22
2
1
1
2
2
1
l
2
= l+∆l = 0,09+0,16 = 0,25 м
Ответ: l
1
= 9 см, l
2G
=G25Gсм.
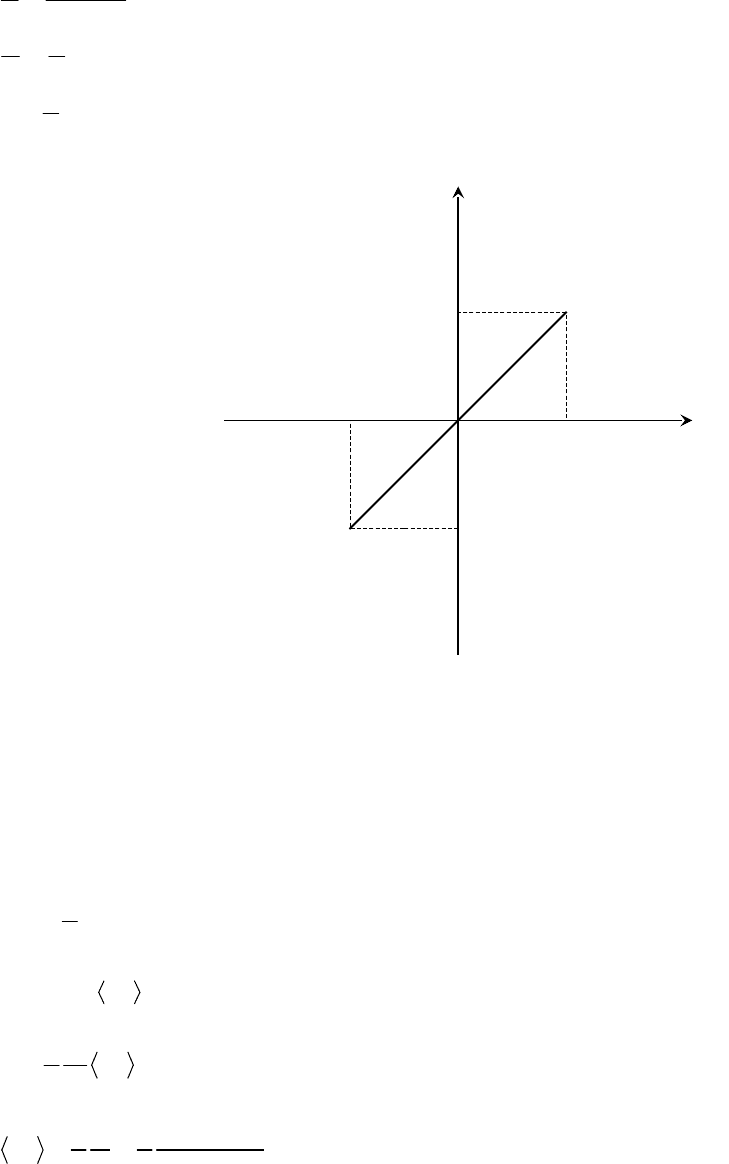
5.38 Точка участвует одновременно в двух гармонических колебаниях, происходящих во
взаимно перпендикулярных направлениях и описываемых уравнениями x = 3cosωt, см и
уR=R4cosωt, см. Определить уравнение траектории точки и вычертить ее с нанесением
масштаба. Ответ: y=R4х/3.
Решение:
wty
wtx
cos4
cos3
wt
wt
x
y
cos3
cos4
3
4
x
y
xy
3
4
Данная линия – отрезок прямой
6.8 Определить среднюю кинетическую энергию <E
0
> поступательного движения
молекул газа, находящегося под давлением 0,1 Па. Концентрация молекул газа равна 10
13
см
-3
. Ответ: 1,5·10
-19
Дж.
Решение:
Основное уравнение молекулярно- кинетической энергии имеет вид:
K
EPV
3
2
Где E
k
– суммарная кинетическая энергия поступательного движения всех молекул
;*
0
ENE
K
N – число молекул
PV = 2/3N <E
0
>
0
3
2
E
V
N
P
n – концентрация молекул
Дж
n
P
E
19
613
0
10*5,1
10*10
1,0
2
3
2
3
Ответ: <E
0
> = 1,5*10
-19
Дж
4
-4
3
-3
0
х
у
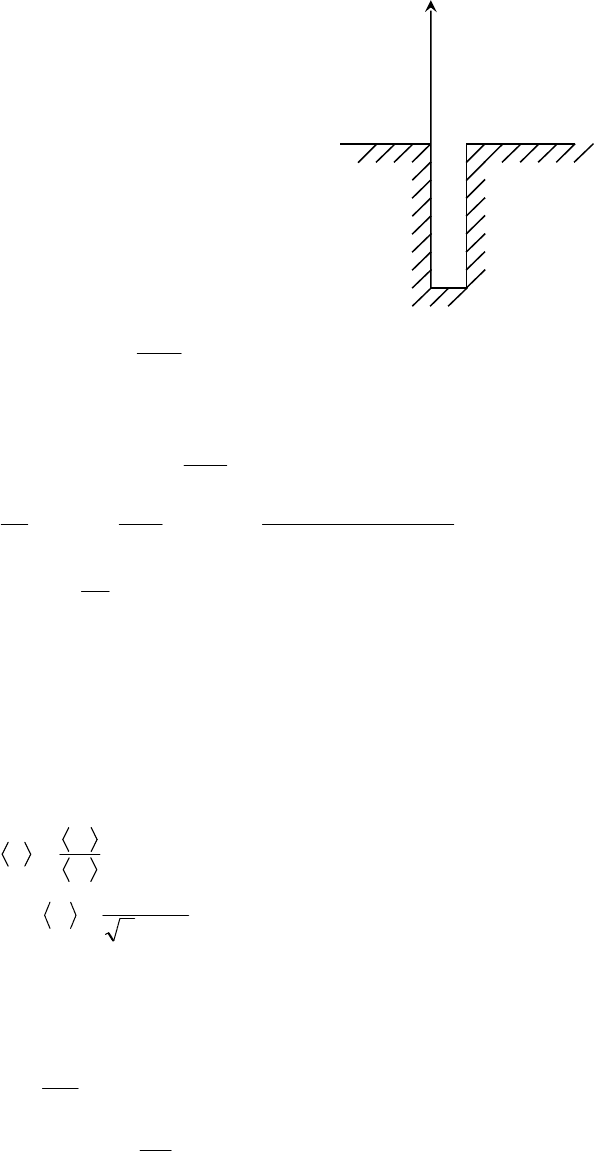
6.13 Определить отношение давления воздуха на высоте 1 км к давлению на дне
скважины глубиной 1 км. Воздух у поверхности Земли находится при нормальных
условиях, и его температура не зависит от высоты Ответ: 0,78.
Решение:
Пусть начало отсчёта находится на дне скважины глубиной 1 км. Тогда убывание
давления с высотой определяется по формуле.
)exp(
0
RT
gy
PP
При у
1
= 0 P
1
= P
0
При у
2
= 2000 м
)exp(
02
RT
gy
PPP
778,0)251,0exp()
273*31,8
2000*81,9*029,0
exp()exp(
1
2
RT
gy
P
P
Ответ:
778,0
1
2
P
P
6.17 Определить среднюю продолжительность <τ> свободного пробега молекул водорода
при температуре 27 °С и давлении 5RкПа. Диаметр молекулы водорода' принять равным
0,28 нм. Ответ: 13,3 нс.
Решение:
Среднюю продолжительность свободного пробега найдём по формуле:
V
l
0
Где
n
l
2
0
2
1
- средняя длина свободного пробега;
σ = 0,28*10
-9
– эффективный диаметр молекулы;
n – концентрация молекул;
Из уравнения Менделеева – Клапейрона имеем:
PV = VRT;
RT
N
N
P
A
;
p=nkT →
kT
P
n
;
где к – постоянная Больцмана;
0
у
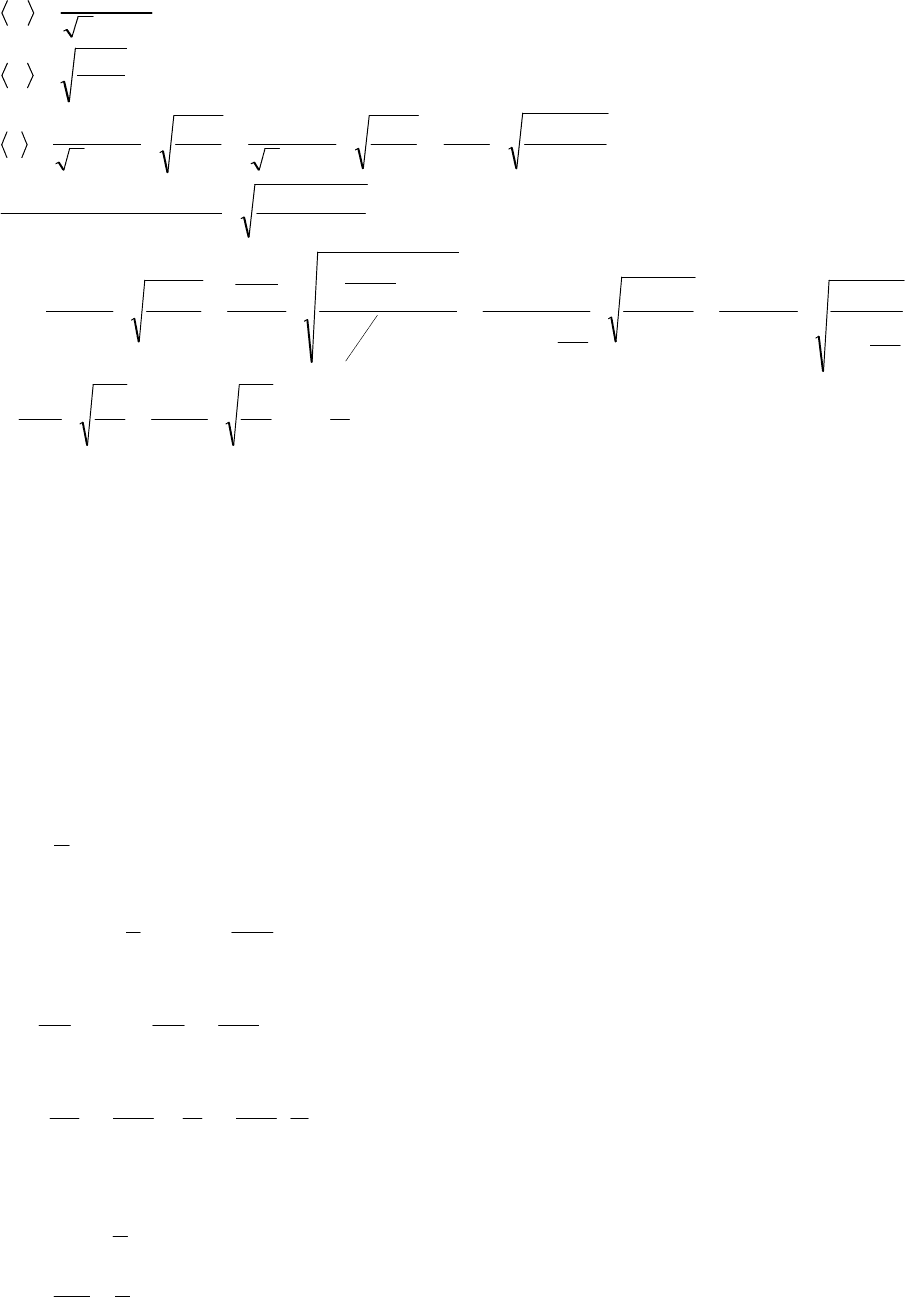
Т – температура газа;
RT
V
P
kT
l
8
2
2
0
c
RT
T
P
k
RT
P
kTRT
P
kT
11
329
23
2
2
2
22
10*44,5
5000*
300*002,0
*
10*5*)10*28,0(4
10*38,1
16
*
8
*
2
8
*
2
с
м
с
м
м
с
Н
мН
м
с
Н
Дж
с
м
кг
кг
НК
КДж
Дж
Ккг
м
Н
мк
Дж
кмоль
Дж
К
моль
кг
Пам
к
Дж
R
T
p
k
**
*
*
*
*
*
**
*
**
)*(
*
**
2
2
2
2
2
2
2
2
2
22
Ответ: <τ> = 5,44*10
-11
c = 54,4 мс
7.8 Применяя первое начало термодинамики и уравнение состояния идеального газа,
показать, что разность удельных теплоемкостей с
р
R–R c
V
= R/M.
Решение:
Q = A + ∆U
Где Q – количество теплоты, полученное газом;
A – работа газа;
∆U – изменение его внутренней энергии при постоянном давлении:
A = p∆V = ∆(PV);
Где, согласно уравнению состояния идеального газа;
PV = υRT → ∆(PV) = υR∆T
TR
i
u
2
;
При постоянном давлении:
TR
i
TR
i
TRQ
p
2
2
2
;
Теплоёмкость газа определяется соотношением:
R
i
T
Q
C
T
Q
C
p
p
2
2
;
Тогда удельная теплоёмкость при р=const;
Ri
m
R
i
m
C
C
p
p
2
2
2
2
;
При V=const:
А=0
TR
i
UQ
V
2
;
R
i
AT
Q
C
V
V
2
;
