Контрольная работа - Термодинамика
Подождите немного. Документ загружается.

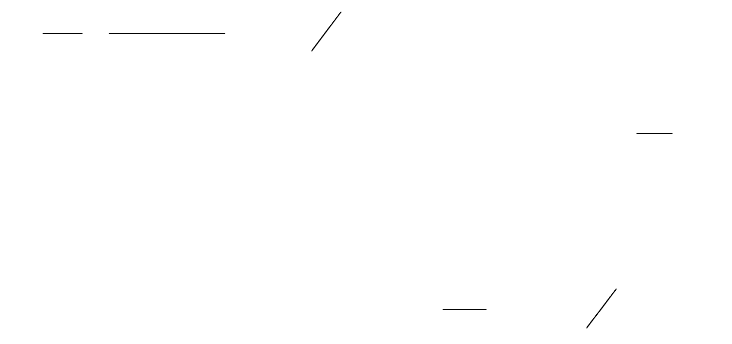
задача № 1
Газ – воздух с начальной температурой t
1
= 27 ºC сжимается в одноступенчатом
поршневом компрессоре от давления Р
1
= 0,1 мПа до давления Р
2
= 0,9 мПа. Сжатие может
происходить по изотерме, по адиабате и по политропе с показателем политропы
n = 1,24. Определить для каждого из трех процессов сжатия конечную температуру газа
Т
2
, отведенную от газа теплоту q и теоретическую мощность компрессора, если его
производительность G = 0,3 ∙ 10
3
кг/ч. Дать сводную таблицу и изображение процесса
сжатия в P-V и T-S диаграммах.
ДАНО : Определить:
Т
1
= 27 + 273, 15 = 300,15 К T
2
; N
T
; q
Р
1
= 0,1 мПа ; Р
2
= 0, 9 мПа ;
G= 0,3 ∙ 10
3
кг/ч ; n = 1,24
Указание: Расчет произвести без учета зависимости теплоемкости от температуры.
Решение
Примем значения теплоемкостей при постоянном давлении С
Р
и постоянном объеме
С
V
равными : С
Р
= 1, 00455 кдж/кг∙ К. ; С
V
= 0, 717 кдж/кг ∙ К.
Найдем начальный удельный объем воздуха при заданных условиях :
кг
м
P
RT
3
6
1
1
86,0
101,0
15,300287
где R = 287 дж/кг ; К – газовая постоянная для воздуха ;
4,1
V
p
C
C
k
Изотермический процесс
Удельный объем воздуха после сжатия при Т
1
= Const будет определяться из
соотношения Pυ = RT и P
1
υ
1
= P
2
υ
2
;
кг
м
P
P
3
2
11
2
095,0
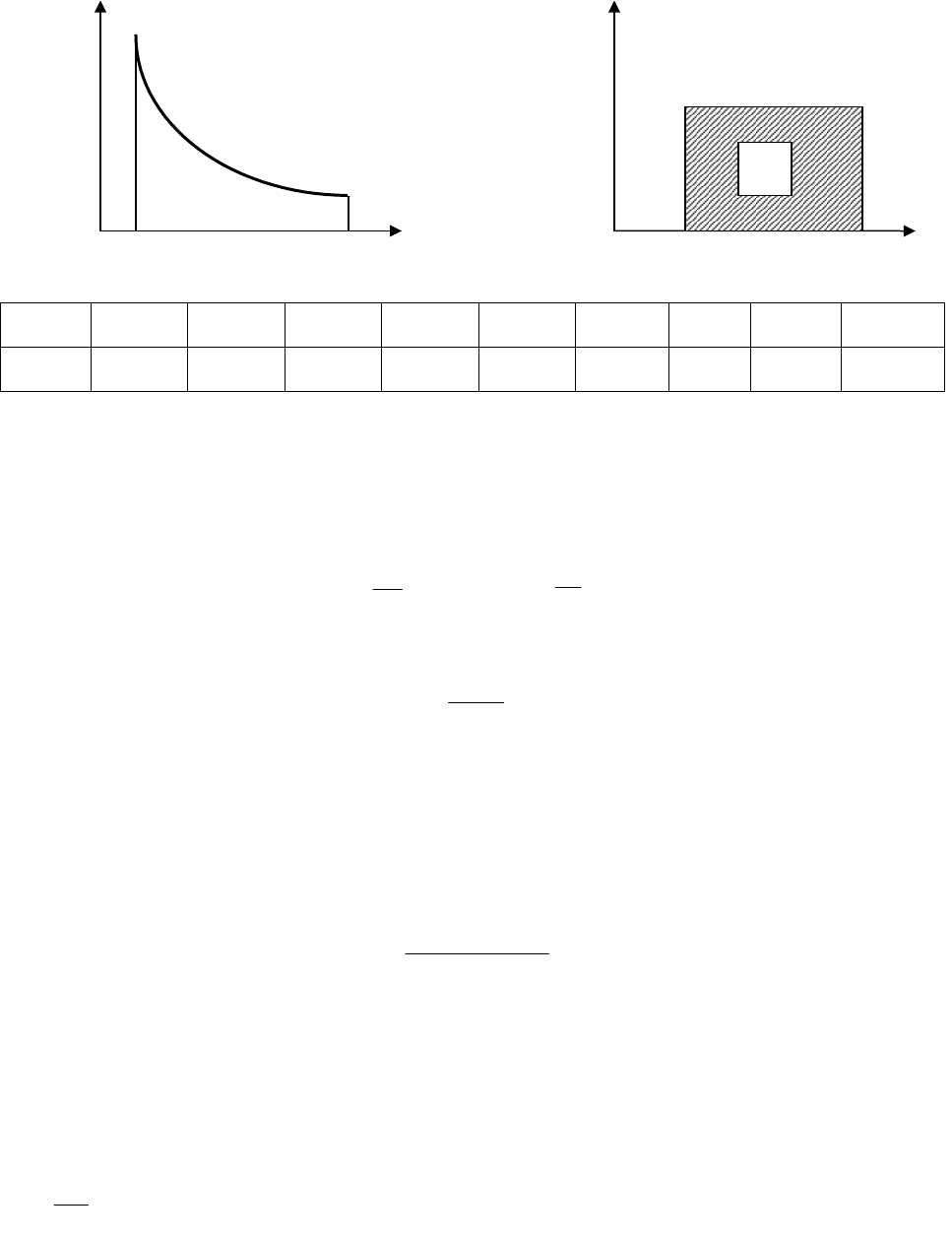
P
2
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
V
2
0,86 0,43 0,37 0,21 0,17 0,14 0,122 0,1 0,095
В соответствии с Ι законом термодинамики при Т = Const количество теплоты,
отводимой от компрессора, равно работе сжатия dq = du + dυ
du = 0 ; dq = Pdυ ;
d
RTPddl
;
1
2
ln
RTl
ñæ
;
6,189
86,0
095,0
ln300287
ñæ
l
кДж/кг
В соответствии с формулой (1) работа компрессора равна работе сжатия
l
k
= l
сж
, т.е. l
k
= 189,6 кДж/кг .
Тогда мощность компрессора равна :
8,15
3600
103,06,189
3
kT
GlN
кВт
Адиабатический процесс
Этот процесс происходит без теплообмена с внешней средой : dq= 0
Уравнение адиабаты идеального газа Pυ
k
= Const, значит P
1
υ
1
k
= P
2
υ
2
k
, где
4,1
v
p
C
C
k
– показатель адиабаты
Соотношение между параметрами в адиабатическом процессе :
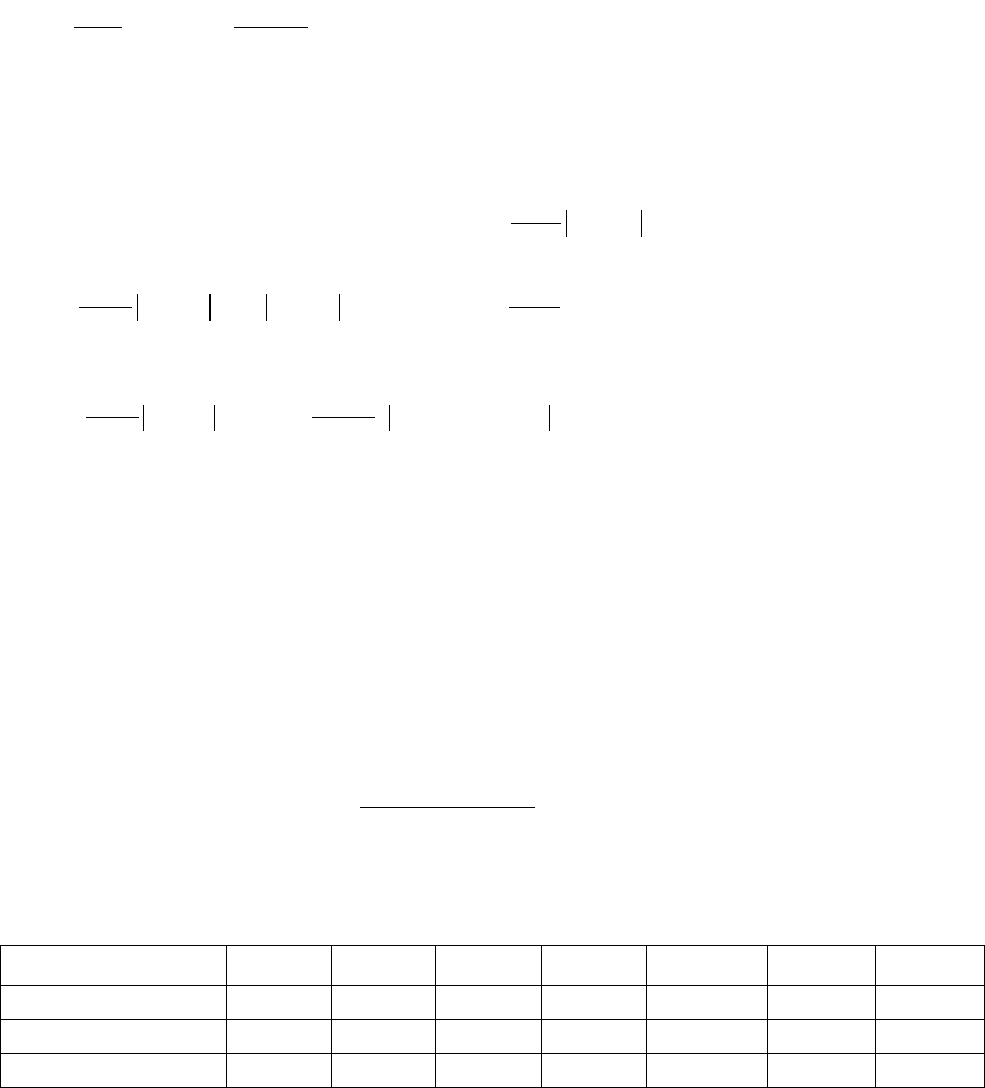
P
L
с
1
V
2´
q
q
T
S
1 2
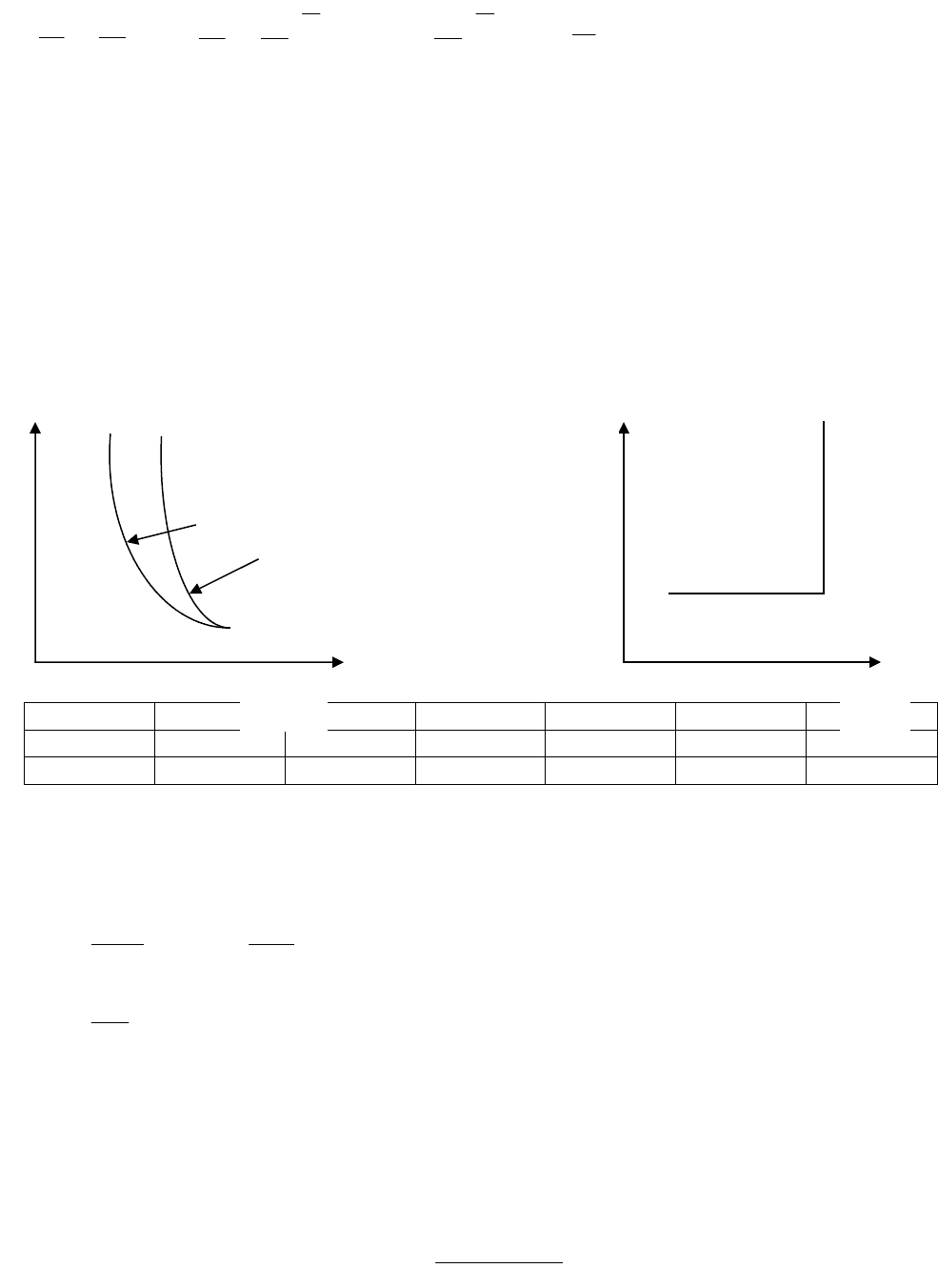
;
1
2
1
1
2
k
T
T
;
1
1
2
1
2
k
k
P
P
T
T
;
1
1
2
12
k
k
P
P
TT
kk
P
P
1
2
1
2
P 0,1 0,2 0,3 0,4 0,7 0,9
V 0,86 0,523 0,392 0,319 0,214 0,178
T 300,15 366 411 446 525 565
Тогда 1-й закон термодинамики для адиабатического процесса имеет вид :
0 =du + dl ; dl = C
v
dT , тогда работа сжатия будет равна l
сж
= C
v
(T
1
-T
2
).
;
1
1
1
221121
PP
k
TT
K
R
l
ñæ
565300
4,0
287
ñæ
l
- 190,005 кДж/кг
Работа компрессора l
k
= k ∙ l
сж
= 266
Теоретическая мощность компрессора :
22
3600
26610003,0
kk
lGN
кВт
2´´
1
S=Const
2´
PV = Const
PV
k
=Const
SV
2´ 2´´Р
PV=Const
PV
k
=Const
1
T
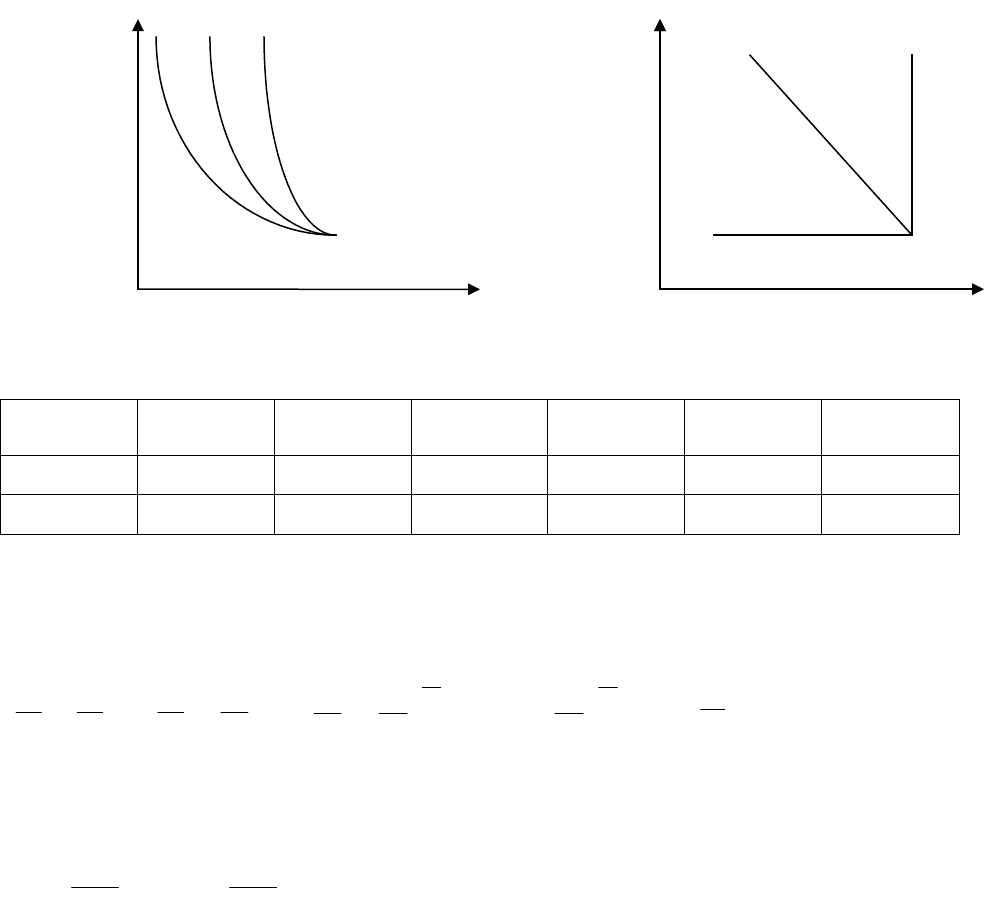
Политропический процесс
В политропическом процессе происходит изменение газа с изменением всех
параметров. Уравнение политропного процесса имеет вид:
Рυ
n
= Const , где n – показатель политропы.
P 0,1 0,2 0,3 0,4 0,7 0,9
V 0,86 0,492 0,354 0,281 0,179 0,146
T 300 343 371 393 438 458,67
Для различных политропических процессов n может принимать любые значения
от + ∞ до - ∞ . Соотношения между параметрами в политропном процессе :
;
2
1
1
2
n
P
P
;
1
2
1
1
2
n
T
T
;
1
1
2
1
2
n
n
P
P
T
T
;
1
1
2
12
n
n
P
P
TT
nn
P
P
1
2
1
2
Работу сжатия воздуха в политропическом процессе можно определить по следующим
формулам :
;
1
1
1
221121
PP
n
TT
n
R
l
ñæ
S
1
2´´
2
2´
T
S
1
22 2´´
2´ Р
кгкДжTT
n
R
l
сж
/56,18967,45815,300
124,1
287
1
21
Количество отведенной в процессе сжатия теплоты можно определить с
помощью 1-го закона термодинамики dq = du + dl . Учитывая что :
∆U = C
v
(T
1
– T
2
) ; ∆U = C
v
│T
1
– T
2
│;
;
1
12
TT
n
R
l
q =
,
1
1212
TTCTT
n
kn
C
nv
где
1
n
kn
CC
vn
- теплоемкость идеального газа в
политропном процессе,
кгкДжTT
n
kn
Cq
v
/77,7515,30067,458
24,0
16,0
717,0
1
12
Изменение внутренней энергии ∆U = U
2
– U
1
= C
v
│T
2
– T
1
│ = 113,66 кДж/кг
Проверим q = ∆U + l = 113,66 – 189,56 = - 75,8 кДж/кг
Работа компрессора будет равна : l
к
= l
сж
∙ n ; l
k
= 1,24 ∙ 189,56 = 235,05
Тогда теоретическая мощность компрессора :
кВтN
T
58,19
3600
05,23510003,0
Сводная таблица полученных результатов
Процесс υ
2
T
2
q l
k
l
сж
N ∆U
Изотермический 0,86 300 -189,6 189,6 189,6 15,8 0
Адиабатический 0,178 565 0 266 -190,005 22 190,005
Политропический 0,146 458,7 -75,8 235,05 189,56 19,9 113,66
Задача № 2
Водяной пар с начальным давлением Р
1
= 3 МПа и степенью сухости Х
1
= 0,95
поступает в пароперегреватель , где его температура повышается на ∆t = 210 ºС после
перегревателя пар изоэнтропно расширяется в турбине до давления Р
2
= 3 кПа .
Определить (по h-S диаграмме) количество теплоты (на 1 кг пара), подведенной
к нему в пароперегревателе , работу цикла Ренкина и степень сухости пара Х
2
в конце

расширения. Определить также термический кпд цикла. Определить работу цикла и
конечную степень сухости , если после пароперегревателя пар дросселируется до
давления
1
= 0,5 МПа.
Дано : Определить :
Р
1
= 3 МПа, Х
1
= 0,95, ∆t = 210 ºС, q
1-2
; X
2
; l
2-3
;
Р
2
= 3 кПа ,
1
= 0,5 МПа
3
; l
2-3
;
е
Решение
Точка исходного состояния пара на h-S диаграмме лежит на пересечении
изобары Р
1
= 3 МПа , и линии сухости пара Х
1
= 0,95. Энтальпия пара , соответствующая
этой точке : h
1
= 2730 кДж/кг.
Точка 2 соответствующая состоянию пара после перегрева, лежит на пересечении
той же изобары Р
1
= 3 МПа и изотермы с температурой t
2
= t
1
+ ∆t ,
где t
1
= 235 ºC , t
2
= 235 + 210 = 445 ºC.
Энтальпия пара в точке 2 h
2
= 3340 кДж/кг (по диаграмме). При этом количество
теплоты, подведенное к пару при перегреве (для изобарного процесса),
q
1-2
= h
2
– h
1
= 3340 – 2730 = 610 кДж/кг
После изоэнтропного расширения пара в турбине его состояние будут
определять параметры , соответствующие точке 3. Ее находят на пересечении
вертикальной линии, опущенной из точки 2 на изобару Р
2
= 3 кПа. Энтальпия пара в точке
3 h
3
= 2100 кДж/кг,
при этом степень сухости после расширения Х
2
= 0,819 (по диаграмме).
Работа цикла Ренкина l
2-3
= h
2
– h
3
= 3340 – 2100 = 1240 кДж/кг
Термодинамический кпд цикла Ренкина :
382,0
1043340
1240
11
2
32
2
kn
ц
k
ц
t
hh
hh
qhh
Если после перегрева пар дросселируется, то процесс дросселирования
происходит при постоянной энтальпии. Этот процесс изображается горизонтальной
линией. Точка 2´, соответствующая состоянию пара после дросселирования , лежит
на пересечении изобары Р
1
´= 0,5 МПа и горизонтальной линией, проведенной из точки 2
Энтальпия h
2
´ = h
2
= 3340 кДж/кг.
Расширение пара в турбине также изображается вертикальной линией
опущенной из точки 2´ до пересечения с изобарой Р
2
= 3 кПа (точка 3´). Энтальпия
пара в точке 3´ h
3´
= 2340 кДж/кг.
Работа пара в цикле Ренкина l
2´-3´
= h
2´
- h
3´
= 3340 – 2340 = 1000 кДж/кг
Степень сухости пара после расширения Х
3´
= 0,919 (по диаграмме).

кпд цикла -
306,0
1043340
990
t
Задача № 3
По горизонтально расположенной стальной трубе (λ = 20 Вт/м ∙ К) со
скоростью W = 0,27 м/с течет вода , имеющая температуру t
В
= 140 ºС . Снаружи вода
охлаждается окружающим воздухом , температура которого t
Воз
= 18 ºС , а давление
0,1 МПа. Определить коэффициенты теплоотдачи α
1
и α
2
соответственно от воды к
стенке трубы и от стенки трубы к воздуху ; коэффициент теплоотдачи и тепловой поток
q
1
, отнесенный к 1 м трубы , если внутренний диаметр трубы d
1
=190 мм, внешний
d
2
= 210 мм. Для определения α
2
принять в первом приближении температуру наружной
поверхности трубы t
2
равной температуре воды.
Дано Определить
λ = 20 Вт/ м ∙ К, W = 0,27 м/с , t
В
= 140 ºС α
1
, α
2
, q
1
, К
t
Воз
= 18 ºС, d
1
= 190 мм , d
2
= 210 мм
Решение
По условию задачи необходимо определить коэффициент теплопередачи
и соответствующий тепловой поток q = K ∙ π(t
В
– t
Воз
) ,
где К =
221
2
11
1
ln
2
11
1
dd
d
d
- коэффициент теплоотдачи
Для этого вначале необходимо определить коэффициент теплоотдачи от
воды к трубе – α
1
и от трубы к воздуху – α
2
.
Выясним характер течения воды в трубе , для чего подсчитаем численное
значение критерия Рейнольдса :
5
7
1041,2
1012,2
19,027,0
Re
Wd
, где ν – кинематический коэффициент вязкости
воды (взят из таблицы) , Re > R
кр
– следовательно , режим движения жидкости внутри
трубы турбулентный.
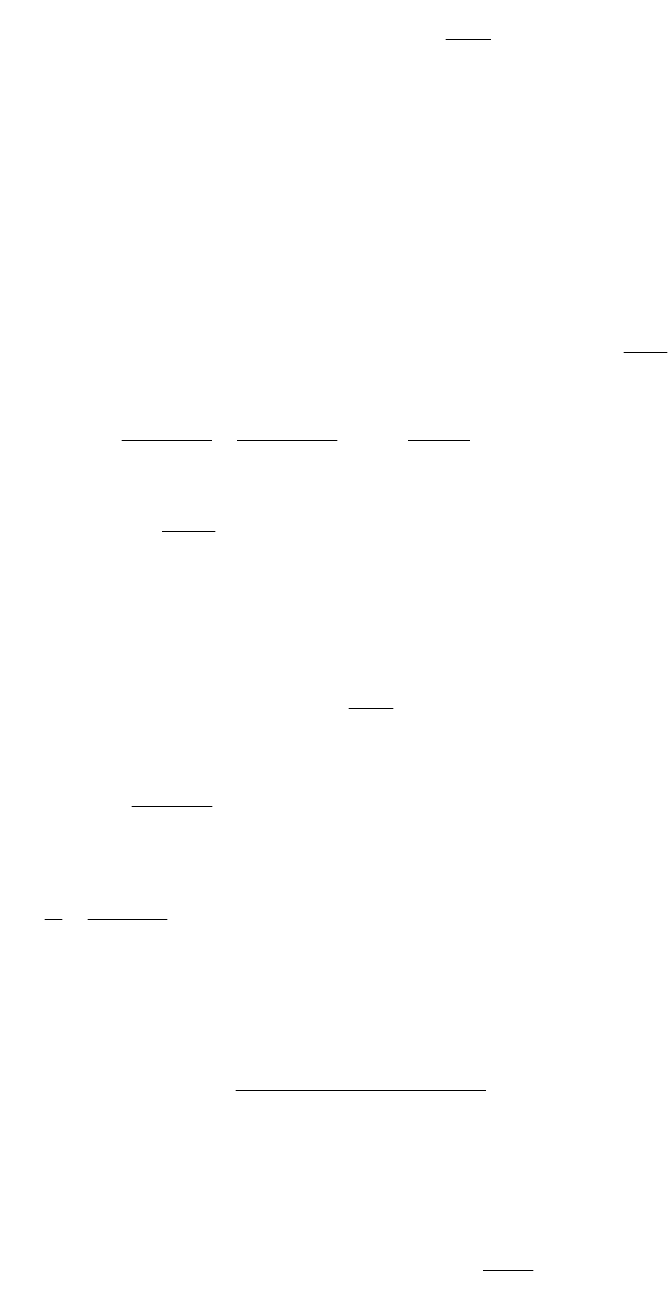
Для расчета среднего значения коэффициента теплоотдачи используем формулу
М.А. Михеева для Nu , полученную на основании обобщения результатов многих
экспериментов для турбулентного режима течения.
25,0
43,08,0
Pr
Pr
PrRe021,0
ст
ж
ж
Nu
Возьмем из таблиц значение критерия Прандтля для температуры t = 140 ºC
Pr
ж
= 1,23.
Принимаем в первом приближении t º внутренней поверхности стенки трубы
равной t º жидкости, тогда Pr
ст
= Pr
ж
= 1,23
Критерий Нуссельта будет равен :
Nu
ж
= 0,021 ∙ (2,41 ∙ 10
5
)
0,8
∙ 1,23
0,43
∙ 1
0,25
= 464 ; т.к.
d
Nu
.
Тогда
Км
Вт
d
Nu
жж
2
1
1
1939
19,0
794,0464
,
где
Км
Вт
ж
794,0
- при t = 140 ºC для воды.
Для свободной (естественной) конвекции у горизонтальной трубы используется
критериальное уравнение
Nu
ж
= 0,5 ( Gr
ж
∙ Pr
ж
)
0,25
∙
25,0
Pr
Pr
ж
ж
,
где
;
2
3
tgd
Gr
ж
- коэффициент температурного расширения ;
12218140;
18273
11
жст
ttt
Т
ºС ; ν – коэффициент вязкости воздуха
при t = 18 ºС, ν = 15,5 ∙ 10
– 6
м
2
/с
8
2
6
3
1059,1
105,15
12221,081,900346,0
ж
Gr
Pr
ж
– число Прандтля для воздуха при t =18 ºC , Pr
ж
= 0,7 (по таблицам ) ,
Pr
ст
– число Прандтля для воздуха при t = 170 ºC , Pr
ст
= 0,68 (по таблицам).
Nu
ж
= 0,5(1,59 ∙ 10
8
∙ 0,7)
0,25
∙
25,0
68,0
7,0
= 51,7 ;

так как Nu
ж
=
Км
Вт
где
d
Nu
d
ж
жж
2
2
2
0025,0,,
- коэффициент теплопроводности
воздуха при t = 18 ºC ;
Км
Вт
2
2
15,6
21,0
025,07,51
Коэффициент теплопередачи для трубы :
912,1
21,015,6
1
19,0
21,0
ln
202
1
19,01939
1
1
1
ln
2
11
1
221
2
11
dd
d
d
K
К = 1,9
Км
Вт
Тепловой поток, отнесенный к 1м трубы, q
1
=K ∙ π (t
B
– t
Воз
) ,
q
1
= 1,9 ∙ 3,14 ∙ ( 140 – 18 ) = 728 Вт/м .
Задача № 4
Определить поверхность нагрева рекуперативного газовоздушного
теплообменника при прямоточной и противоточной схемах движения теплоносителей,
если объемный расход нагреваемого воздуха при нормальных условиях V
H
=3000 м
3
/час
средний коэффициент теплопередачи от продуктов сгорания к воздуху К = 20 Вт/м
2
∙ К
начальные и конечные температуры соответственно : t´
1
=600 ºC , t´´
1
=400 ºC , t´
2
= 20 ºC
t´´
2
= 300 ºC. Изобразить графики изменения температур теплоносителей для обоих
случаев.
Дано Определить
V
H
= 3000 м
3
/час , К = 20 Вт/м ∙ К F , m
2
t´
1
= 600 ºC , t´´
1
= 400 ºC , t´
2
=20 ºC
t´´
2
=300 ºC
Решение:
Мощность теплообменника определится из выражения :
Q = m
2
C
p
(t´´
2
– t´
2
) , где m
2
– массовый расход воздуха ;
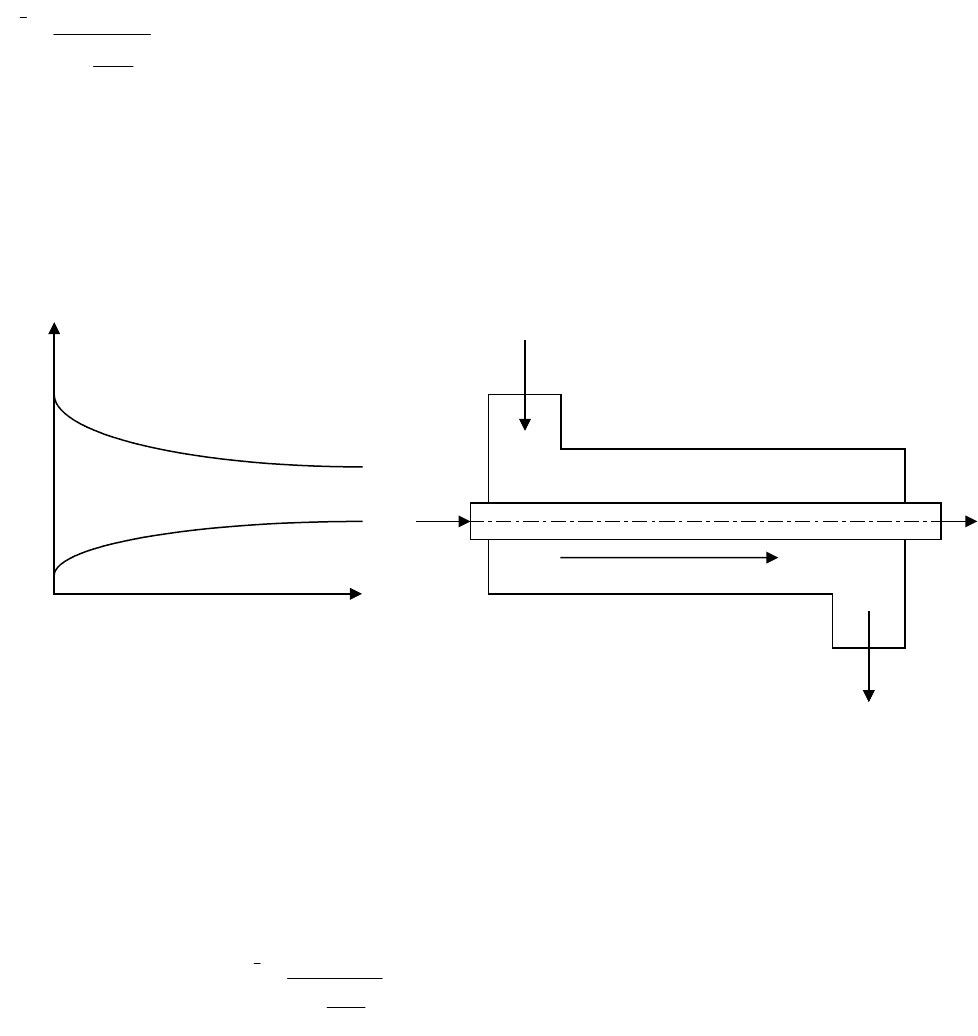
С
р
– изобарная массовая теплоемкость воздуха ;
t´´
2
, t´
2
– тем-ра воздуха на выходе и входе в теплообменник..
Для воздуха без учета температуры С
р
= 1,009 кДж/кг ∙ К, ρ =1,293 кг/м
3
.
тогда m
2
= V
H
∙ ρ = 3000 ∙ 1,293 / 3600 = 1,08 кг/с
Q = 1,08 ∙ 1,009 (300 – 20) = 305,1 кВт
Среднелогарифмический температурный напор в теплообменнике:
m
m
t
t
tt
t
6
6
ln
, где ∆t
6 ,
∆t
m
– соответственно большая и меньшая разность температур
теплоносителей на концах теплообменника.
Для прямоточной схемы :
∆t
6
= 600 – 20 =580 ºC , ∆t
m
= 400 – 300 = 100 ºC ,
273
100
580
ln
100580
t
ºC
