Контрольная работа - Теоретические основы управления

Задача 1

Матричный расчёт токов и напряжений электрической сети.

а) Рассчитать токи в узлах цепи;

б) рассчитать напряжение в узлах цепи.

Исходные данные:

R

1

9:= Ом R

2

7:= Ом R

3

5:= Ом R

4

6:= Ом R

5

1:= Ом R

6

10:= Ом

E

6

11.1:= кВ I

6

3.7:= кА

По исходным данным составим диагональную матрицу сопротивлений

ветвей R, а также вектор столбец источников напряжения U и тока I

R

1

0

R

2

0

R

3

0

R

4

0

R

5

0

R

6

⎛

⎜

⎝

⎞

⎟

⎠

:= U

0

E

6

⎛

⎜

⎝

⎞

⎟

⎠

:= I

0

I

6

⎛

⎜

⎝

⎞

⎟

⎠

:=

1. Для расчета токов в ветвях используют метод контурных токов,

основанный на втором законе Кирхгофа для независимых контуров

SR⋅ S

T

⋅

()

X⋅ SU⋅=

01

2

3

R6

R4

R5

R1

R2 R3

E6

I

II III

Схема для расчёта представлена на рис. 1

Рисунок 1 Схема для расчёта по методу контурных токов

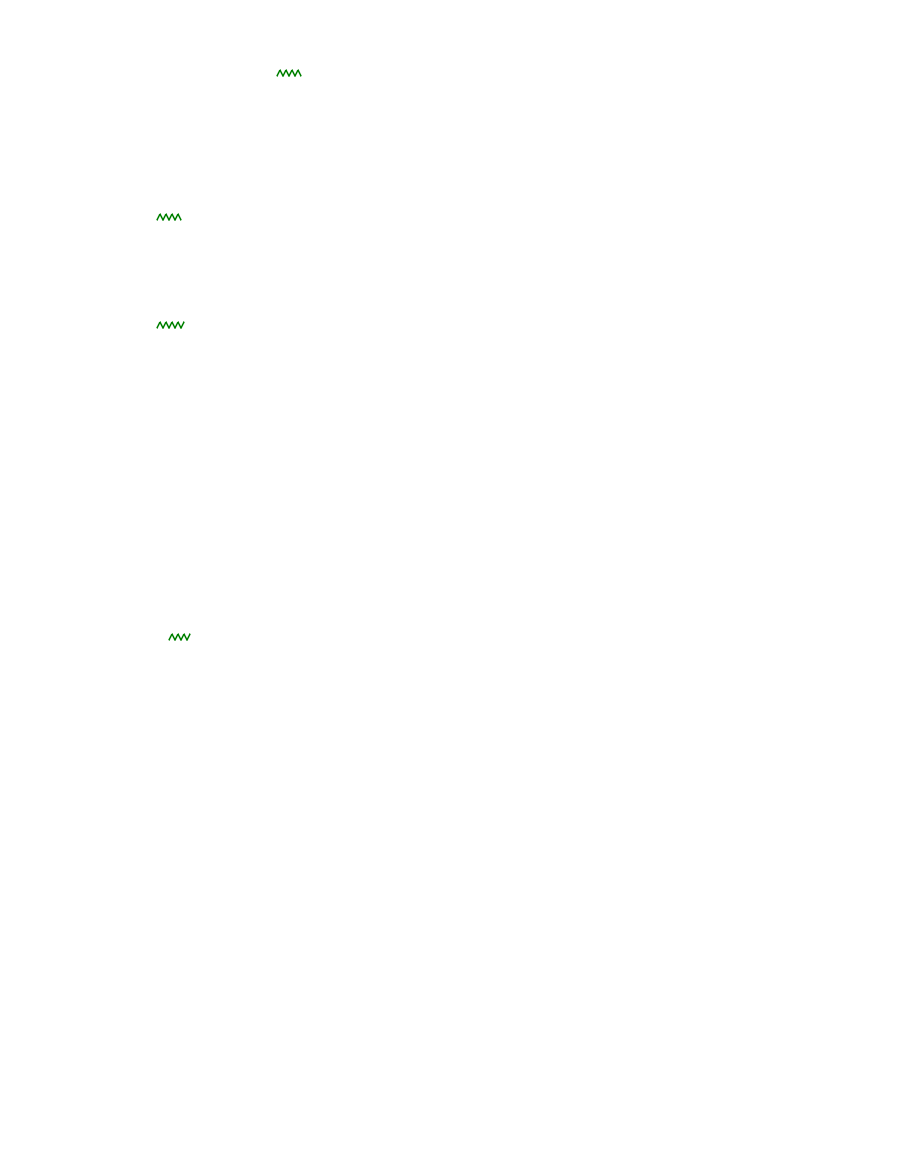
Составим матрицу инциденций (S), описывающую связь с контурами.

S

1

0

1−

1

0

1−

0

1

0

1

1−

0

1

0

1−

0

⎛

⎜

⎝

⎞

⎟

⎠

:=

Введём обозначение для матрицы сопротивлений (А)

A SR⋅ S

T

⋅

()

:= A

21

7−

5−

7−

23

6−

5−

6−

12

⎛

⎜

⎝

⎞

⎟

⎠

= Ом

Обозначим столбец свободных членов (С)

C SU⋅:=

C

0

11.1−

0

⎛

⎜

⎝

⎞

⎟

⎠

= кВ

Определим токи контуров (X)

XA

1−

C⋅:= X

0.366−

0.729−

0.517−

⎛

⎜

⎝

⎞

⎟

⎠

= кА

Определим токи в ветвях (J)

J S

T

X⋅:= J

0.366−

0.363−

0.151−

0.212−

0.517−

0.729

⎛

⎜

⎝

⎞

⎟

⎠

= кА

Проверка по первому закону Кирхгофа:

J

0

J

1

+ J

5

+ 0= J

1

J

2

− J

3

− 0= J

0

J

2

+ J

4

− 0= J

3

J

4

+ J

5

+ 0=

2. Для расчёта напряжений в узлах используют метод узловых потенциало

в

основанный на первом законе Кирхгофа, схема для расчёта на рис. 2

MY⋅ M

T

⋅

()

X⋅ MI⋅=

Составим матрицу инциденций (M), которая даёт связь между узлами схемы

(базисный узел O в неё не включается) и условно выбранными направлениями

токов в ветвях.

M

0

1

0

1

0

1−

1

0

1−

0

1

0

1−

1

0

1

⎛

⎜

⎝

⎞

⎟

⎠

:=

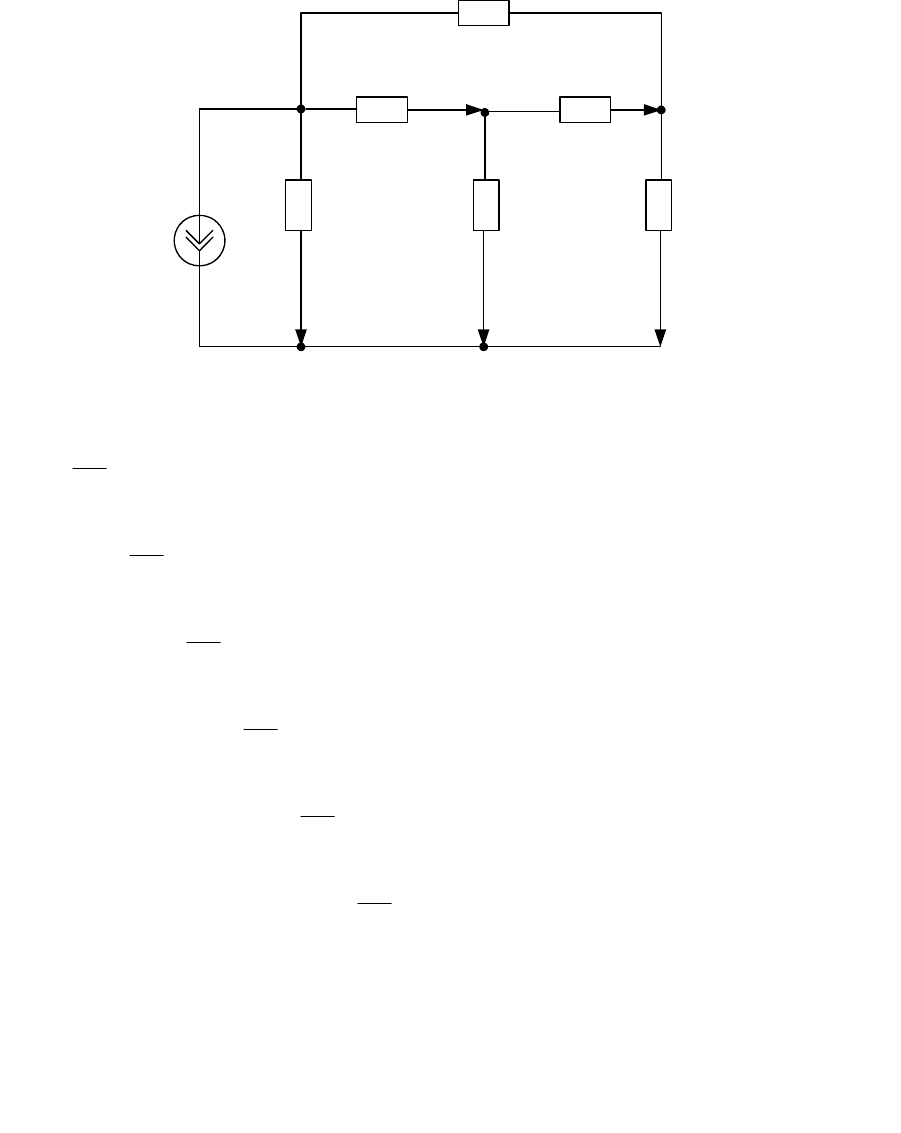
0

1

2

3

R6 R4 R5

R1

R2 R3

I6

Рисунок 2 Схема для расчёта по методу узловых потенциалов

Определим прорводимость Y

MI⋅

0

3.7

⎛

⎜

⎝

⎞

⎟

⎠

=

Y

1

R

1

0

1

R

2

0

1

R

3

0

1

R

4

0

1

R

5

0

1

R

6

⎛

⎜

⎝

⎞

⎟

⎠

:=

MY⋅ M

T

⋅

()

1−

3.612

2.296

2.288

2.296

3.377

2.968

2.288

2.968

3.434

⎛

⎜

⎝

⎞

⎟

⎠

=

Определим напряжение в узлах схемы (u)

uMY⋅ M

T

⋅

()

1−

MI⋅:= u

8.466

10.981

12.704

⎛

⎜

⎝

⎞

⎟

⎠

= кВ

Задача 2

Расчёт установившегося режима в замкнутой сети

1. Определить напряжение в узлах сети;

2. Показать ход итерационного процесса расчёта режима сети.

Исходные данные:

r45:= Ом U

o

135:= кВ P

b

15:= МВт P

c

27:= МВт P

d

63:= МВт

Решение.

1. В расчёте используем матричный способ расчёта сложно замкнутых

сетей

Определим матрицу узловых проводимостей (Yy) и вектор столбец мощности (Р)

Y

y

3

r

1−

r

1−

r

1−

r

3

r

1−

r

1−

r

1−

r

3

r

⎛

⎜

⎝

⎞

⎟

⎠

:= Y

y

0.067

0.022−

0.067

0.022−

0.067

⎛

⎜

⎝

⎞

⎟

⎠

=

P

b

P

c

P

d

⎛

⎜

⎝

⎞

⎟

⎠

:= P

15

27

63

⎛

⎜

⎝

⎞

⎟

⎠

= МВт

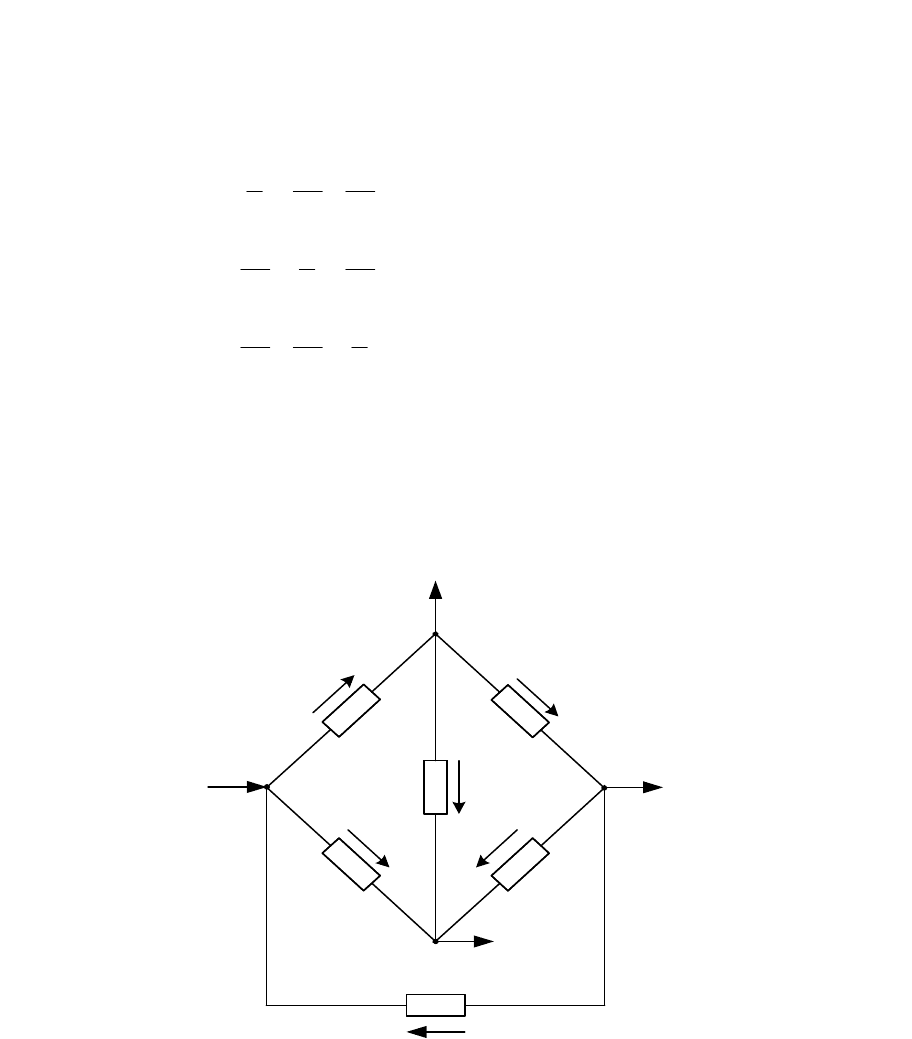
Схема замещения многоконтурной электрической сети представлена на рис.3

i3

jd

i6

i2

i5

i1

i4

jb

b

c

d

Рисунок 3 Схема для расчёта по методу узловых потенциалов

В первом приближении определим токи нагрузок (I

1

) и напряжение (U

1

) при

этих токах

I

1

P3U

o

⋅

()

1−

⋅:= I

1

0.064

0.115

0.269

⎛

⎜

⎝

⎞

⎟

⎠

= кА

U

1

U

o

Y

y

1−

3 I

1

⋅

()

⋅−:= U

1

125

124

121

⎛

⎜

⎝

⎞

⎟

⎠

= кВ

Во втором приближении определим токи нагрузок (I

2

) и напряжение (U

2

) пр

и

этих токах, полагая U

x

= U

1i,

i01, 2..:=

I

2

i

P

i

3 U

1

i

⋅

⎛

⎝

⎞

⎠

1−

⋅:= I

2

0.069

0.126

0.301

⎛

⎜

⎝

⎞

⎟

⎠

= кА

U

2

U

o

Y

y

1−

3 I

2

⋅

()

⋅−:= U

2

124

122.9

119.5

⎛

⎜

⎝

⎞

⎟

⎠

= кВ

В третьем приближении определим токи нагрузок (I

3

) и напряжение (U

3

) пр

и

этих токах, полагая U

x

= U

2i

I

3

i

P

i

3 U

2

i

⋅

⎛

⎝

⎞

⎠

1−

⋅:= I

3

0.07

0.127

0.304

⎛

⎜

⎝

⎞

⎟

⎠

= кА

U

3

U

o

Y

y

1−

3 I

3

⋅

()

⋅−:= U

3

123.875

122.764

119.304

⎛

⎜

⎝

⎞

⎟

⎠

= кВ

И так, в третьем приближении определим токи нагрузок (I

3

) они почти равн

ы

токам нагрузок второго приближения (I

2

), дальнейший расчёт не даст

существенного уточнения, по этому полученный на третьей итерации результат U

будет окончательным решением.

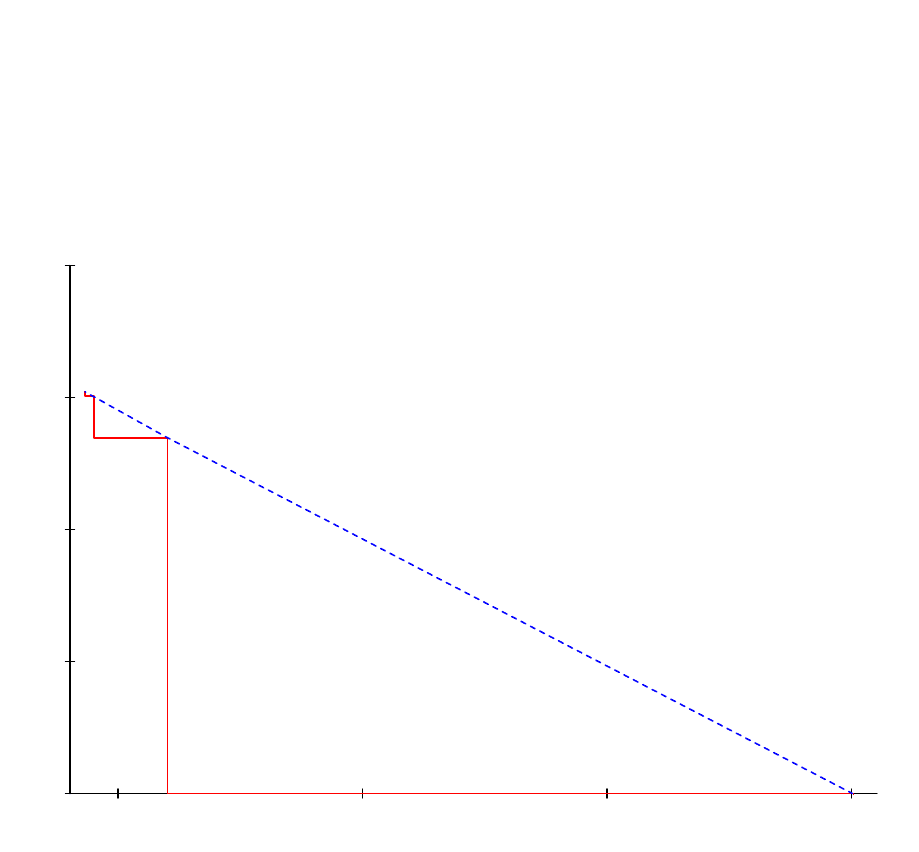
2. Покажем ход итерационного процесса на примере узла d рис. 4.

U

o

U

1

2

U

2

U

3

2

⎛

⎜

⎝

⎞

⎟

⎠

:= I

0

I

1

2

I

2

I

3

2

⎛

⎜

⎝

⎞

⎟

⎠

:= j

0

I

1

2

I

2

I

3

2

⎛

⎜

⎝

⎞

⎟

⎠

:= U

135

121

119.486

119.304

⎛

⎜

⎝

⎞

⎟

⎠

= I

0

0.269

0.301

0.304

⎛

⎜

⎝

⎞

⎟

⎠

=

120 125 130 135

0.1

0.2

0.3

0.4

Рисунок 4 Ход итерационного процесса для одного узла d

Список используемой литературы.

1. Сухов М.Ю. Теоретические основы управления: Задание на контрольную

работу с методическими указаниями. - М.: РГОТУПС - 2004.

2. Герман Л.А. Матричные методы расчёта системы тягового электроснабжения:

Конспект лекции. - Ч. 1 - М.: РГОТУПС, 1998.

3. Герман Л.А. Матричные методы расчёта системы тягового электроснабжения:

Конспект лекции. - Ч. 2 - М.: РГОТУПС, 2000.

Контрольная работа - Теоретические основы управления

Подождите немного. Документ загружается.