Контрольная работа по математическим методам в психологии
Подождите немного. Документ загружается.

МОСКОВСКИЙ ГОРОДСКОЙ
ПСИХОЛОГО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ДИСТАНЦИОННОГО ОБУЧЕНИЯ
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ
КОНТРОЛЬНАЯ РАБОТА
ФИО студента:
Курс 2, семестр 3
ФИО и звание преподавателя:
Сорокова Марина Геннадьевна, доктор педагогических
наук, кандидат физико-математических наук, профессор
Москва
2011

Контрольная работа
1. Дать определение и сравнить на примере «номинальную»,
«порядковую» и «интервальную» измерительные шкалы.
Номинальная шкала - это метрическая шкала, отображающая только отношение
эквивалентности между элементами измеряемой области. Пример: балльные оценки
успеваемости в школе, номера испытуемых в психологических экспериментах.
Порядковая шкала – метрическая шкала, которая отображает наряду с отношением
эквивалентности еще и отношение порядка. Пример: места занятые школьниками в
олимпиаде по математике, ранги результатов психологического эксперимента.
Интервальная шкала – это метрическая шкала, отображающая кроме отношений
наименований и порядка еще и отношение расстояний между парами объектов. Пример:
психологические тесты личности, установок и способностей, абсолютные результаты
психофизиологического исследования, температурная шкала Цельсия.
2. Две нормальные выборки размера 20 и 25 имеют выборочные средние
4,5 и 5,3, и выборочные дисперсий 10,0 и 12,5, соответственно. Можно
ли принять гипотезу о равенстве дисперсии и средних на уровне
значимости а=0,05?
Решение: необходимо воспользоваться правосторонним критерием Фишера. Найдем
значение Fнабл.
F
набл
=S
2
2
/S
1
2
=12,5/10,0=1,25
Так как нам дано α= 0,05, k
1
=n-1=25-1=24, k
2
=m-1=20-01=19 из таблицы
распределения Фишера-Снедекора находим Fкр = 2,56. Так как Fнабл = 1,25< Fкр = 2,56,
то на уровне значимости α= 0,05 гипотеза о равенстве дисперсий принимается.
Для проверки гипотезы о равенстве средних воспользуемся двусторонним
критерием Стьюдента для двух выборок.
1,11
22025
)120(5,12)125(10
2
S
Рассчитаем выборочное значение t
набл
8,0
2520*1,11
25*20)3,55,4(
набл
t
При заданных α= 0,05 и числе степеней свободы n+m-2=43 по таблице распределения
Стьюдента получаем t
кр
= 2,00.
2
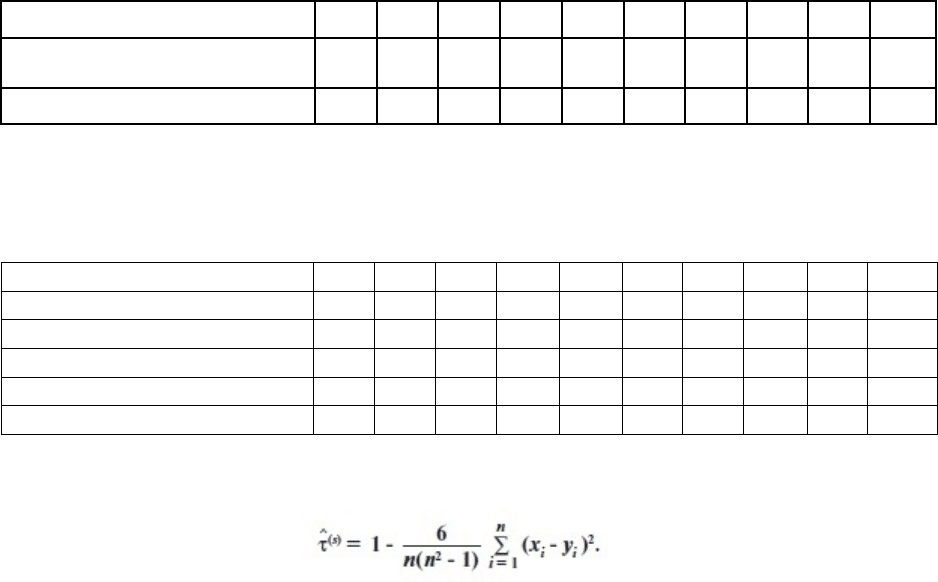
Поскольку |t
набл
| = 0,8< t
кр
=2,0, то на уровне значимости α = 0,05 гипотеза о
равенстве средних принимается.
Так как обе гипотезы приняты с требуемым уровнем значимости, то гипотезу о
равенстве дисперсии и средних на уровне значимости α = 0,05 можно принять.
3. Имеется выборка размера п = 900 с выборочным средним х = 46,5.
Считая, что х имеет асимптотическое нормальное распределение N(m,у
2
/n) при у
2
=25, построить 95%-доверительный интервал для т.
Решение: Среднее квадратическое отклонение исследуемого признака y=5; а
статистическая оценка математического ожидания х=46,5.
Из таблицы значений функций Лапласа для =0,95 находим значение 1,96.
Определяем нижнюю границу доверительного интервала:
α=46,5 – (1,96*5)/√900=46,17
Определяем верхнюю границу доверительного интервала:
α=46,5 + (1,96*5)/√900=46,82
Ответ: значения параметра m согласующиеся с данными выборки удовлетворяют
неравенству:
46,17<m<46,82
4. С помощью коэффициента ранговой корреляции установить зависимость
между стажем практической работы и временем решения контрольной задачи у 10
программистов на основе следующих данных:
Номера испытуемых 1 2 3 4 5 6 7 8 9 10
Стаж (в мес). 32 15 16 18 20 28 21 29 23 17
Время решения (в мин.) 12 24 23 21 20 9 11 10 15 16
Решение:
1). Проранжируем стаж и времена решения задачи. Расчитаем квадраты разностей
рангов стажа и времени решения задачи для каждого испытуемого.
Номера испытуемых 1 2 3 4 5 6 7 8 9 10
Стаж (в мес). 32 15 16 18 20 28 21 29 23 17
ранг 10 1 2 4 5 8 6 9 7 3
Время решения (в мин.) 12 24 23 21 20 9 11 10 15 16
ранг 4 10 9 8 7 1 3 2 5 6
d2 36 81 49 16 4 49 9 49 4 9
2). Подсчитаем сумму d
2
=306.
3). Рассчитаем коэффициент ранговой корреляции по формуле
3
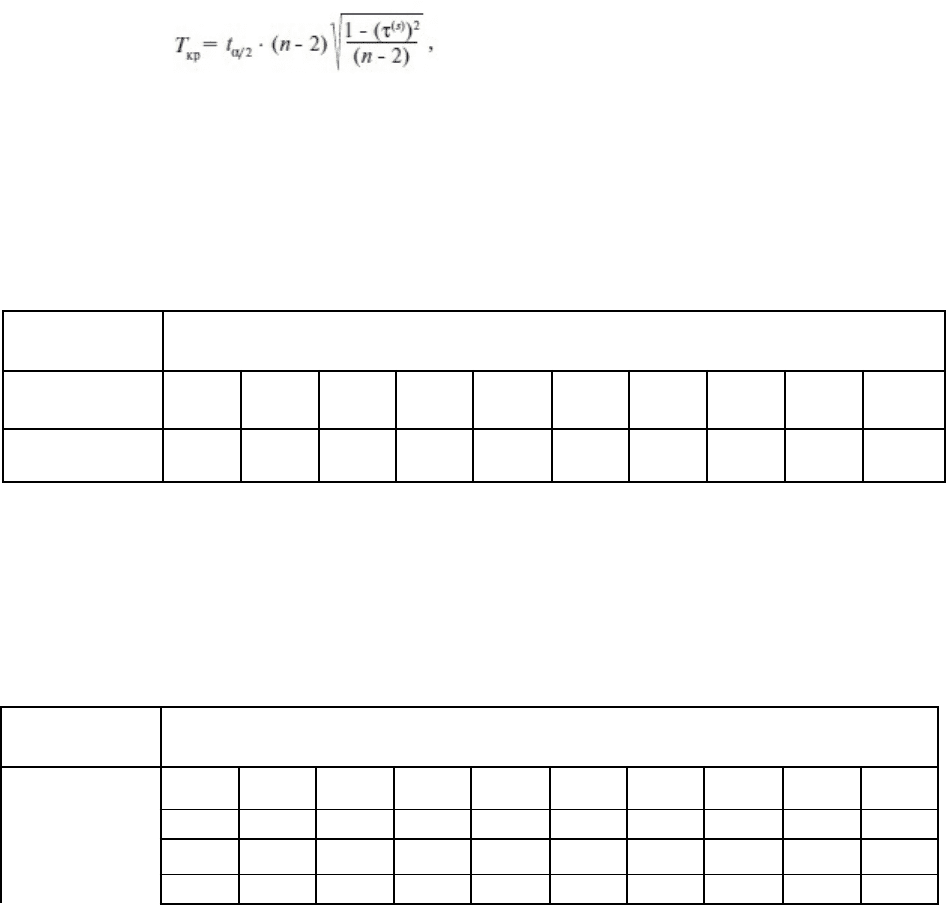
1-6/10/(10*10-1)*306=-0,855. При α = 0,05 и n 2 = 8 из таблицы распределения
Стьюдента находим τ
α/2
(n-2) = 2,306
4). Рассчитаем критическое значение по формуле:
Т
кр
=2,036*(10-2)*((1-(-0,855)
2
)/(10-2))
1/2
=2,987
Поскольку эмпирическое значение превышает критическое, то можно утверждать,
что между стажем практической работы и временем решения контрольной задачи у
программистов есть взаимосвязь.
5. С помощью рангового критерия проверить, уступают ли студенты-физики по уровню интеллекта
студентам-психологам:
Показатели уровня интеллекта
Физики 111 104 107 90 115 107 106 107 95 116
Психологи 113 107 123 122 117 112 105 108 111 114
1) Воспользуемся критерием Манна-Уитни
Формулируем гипотезу H
0
: Показатели уровня интеллекта в обеих группах
испытуемых не различаются.
Формулируем альтернативную гипотезу H
1
: Показатели уровня интеллекта в группе
психологов, выше чем в группе физиков.
2) Проранжируем результаты эксперимента:
Физики
90 95 104 106 107 107 107 111 115 116
1 2 3 5 7,5 7,5 7,5 11,5 16 17
Психологи
105 107 108 111 112 113 114 117 122 123
4 7,5 10 11,5 13 14 15 18 19 20
3). Подсчитаем сумму рангов отдельно для каждой исследуемой группы.
физики: R
1
=1+2+3+5+(7.5*3)+11.5+16+17=78.
психологи: R
2
=4+7.5+10+11.5+13+14+15+18+19+20=132.
4). Рассчитаем статистику U, по формулам:
U
1
=n
1
*n
2
+n
1
*(n
1
+1)/2-R
1
, U
2
=n
1
*n
2
+n
2
*(n
2
+1)/2-R
2 ,
где n
1
, n
2
– количество испытуемых в выборке
U
1
=10*10+10*(10+1)/2 -78=77, U
2
= 10*10+10*(10+1)/2 -132=23
U = min(U
1
, U
2
) = 23.
5). Определим критические значения U
кр
по таблице Критических значения
критерия U Манна-Уитни :
4

U
кр
(n
1
=10; n
2
=10; α=0,05) =27,
U< U
кр
, следовательно гипотеза H
0
отвергается на уровне значимости α=0,05 и
принимается гипотеза H
1
: Уровень умственных способностей у студентов-физиков ниже
уровня умственных способностей у студентов-психологов
6. Используя критерий «хи-квадрат» при уровне значимости а=0.05 проверить,
существует ли зависимость уровня интеллектуального развития учеников от типа
школы по результатам обследования 100 сельских и 100 городских школьников:
Тип школы
Уровень интеллектуального развития
Низкий Нормальный Высокий
Городская 25 50 25
Сельская 52 41 7
1). Формулируем гипотезы:
H
0:
Нет связи между признаками.
H
1:
Есть связь
2). Рассчитаем значение χ
2
по формуле:
При m=2, k=3, n=200
χ
2
=200*(25*25/(77*100)+52*52/25*25/(77*100)+50*50/(91*100)+41*41/
(91*100)+25*25/(32*100)+7*7/(32*100) -1)=20,48
3). Определим по таблице критическое значение
2
2
кр
(0,05; 2) = 5.99;
Так как χ
2
>
2
кр
гипотеза H
0
отвергается на уровне значимости а=0.05.
Следовательно, есть зависимость уровня интеллектуального развития учеников от типа
школы.
7. По нормальной выборке (x
k
. y
k
) , k=1 ... , .....n . размера n = 8
вычислены: ∑x
k
= 278, ∑y
k
=383, ∑x
k
2
=19564,
∑y
k
2
=30995, ∑x
k
y
k
=24484.
Найдя коэффициент корреляции Пирсона, проверить гипотезу о независимости
переменных хиу и построить линию регрессии у по х.
1) Коэффициент корреляции Пирсона рассчитывается по формуле:
5
r=(24484-278*383/8-278/8*383+8*278/8*383/8)/((19564-2*278*278/8+8*278/8* *278/8)
*(30995-2*383*383/8+8*383/8*383/8))
1/2
= 0,998
2) Проверим верность гипотезы по критерию Стъюдента об отсутствии корреляции.
H
0
: r=0
3) Рассчитаем статистику t по формуле : t=r(√n-2)/(√1-r2)
t=0,998*(8-2)
1/2
/(1-0,998*0,998)
1/2
= 3,867
t
кр
(α=0,1; v=n-2=6)=1,94
Так как |t|>t
кр
, то гипотеза H
0
отвергается, следовательно переменные X и Y
зависимы, а
уравнение линейной регрессии имеет вид: y = a + bx
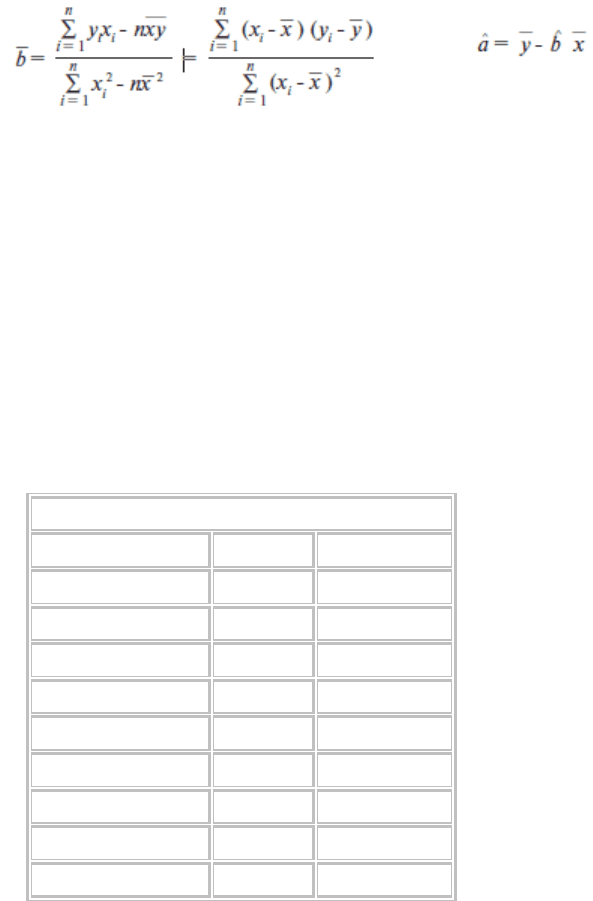
4) Рассчитаем параметры линейной регрессии по формулам:
b=(24484-278*383/8-278/8*383+8*278/8*383/8)/(19564-2*278*278/8+8* *278/8*278/8)=1,13
a=383/8-1,13*278/8=8,6
Уравнение линейной регрессии: y=8,6 + 1,13x
8. Используя анализ однофакторной модели, проверить гипотезу о влиянии
методик на оценку качества признака.
Исследуется эффективность обучения тремя различными методами. Студентам дается задание
изучить тему «Денежная система в Англии». Для этого 10 студентов конспектируют
первоисточник, 10 изучают ее по программированному учебнику, 10 – с помощью обучающих
компьютерных программ. По окончании их уровень знаний проверяется с помощью теста,
состоящего из 100 вопросов. Результаты представлены в таблице:
Баллы по тесту для трех методик
Первоисточник Учебник Компьютер
28 39 41
33 52 49
42 53 56
47 54 62
48 56 63
50 58 64
50 59 65
51 63 72
60 64 77
6
71 77 87
Вопросы: 1) Влияет ли методика изучения темы на результат? Есть ли значимые
различия между тремя выборками по уровню усвоения материала? 2) Есть ли
статистически значимая тенденция возрастания показателей в порядке
«первоисточник» - «учебник» - «компьютер»?
1) Сформулируем гипотезы: Н
0
: a
1
= a
2
= a
3
и альтернативная гипотеза Н
1
о том, что не
все числа a
1
= a
2
= a
3
равны между собой. Гипотеза Н
0
означает, что величина результата
не зависит от способа обработки, т.е. все 3 выборки однородны и образуют объединенную
выборку из общей совокупности, а гипотеза Н
1
означает, что величина результата зависит
от способа обработки.
2) Проранжируем экспериментальные данные и рассчитаем суммы рангов для каждого
метода R
j
.
Баллы по тесту для трех методик
Первоисточник Учебник Компьютер
1 3 4
2 12 8
5 13 15,5
6 14 20
7 15,5 21,5
9,5 17 23,5
9,5 18 25
11 21,5 27
19 23,5 28,5
26 28,5 30
96 166 203
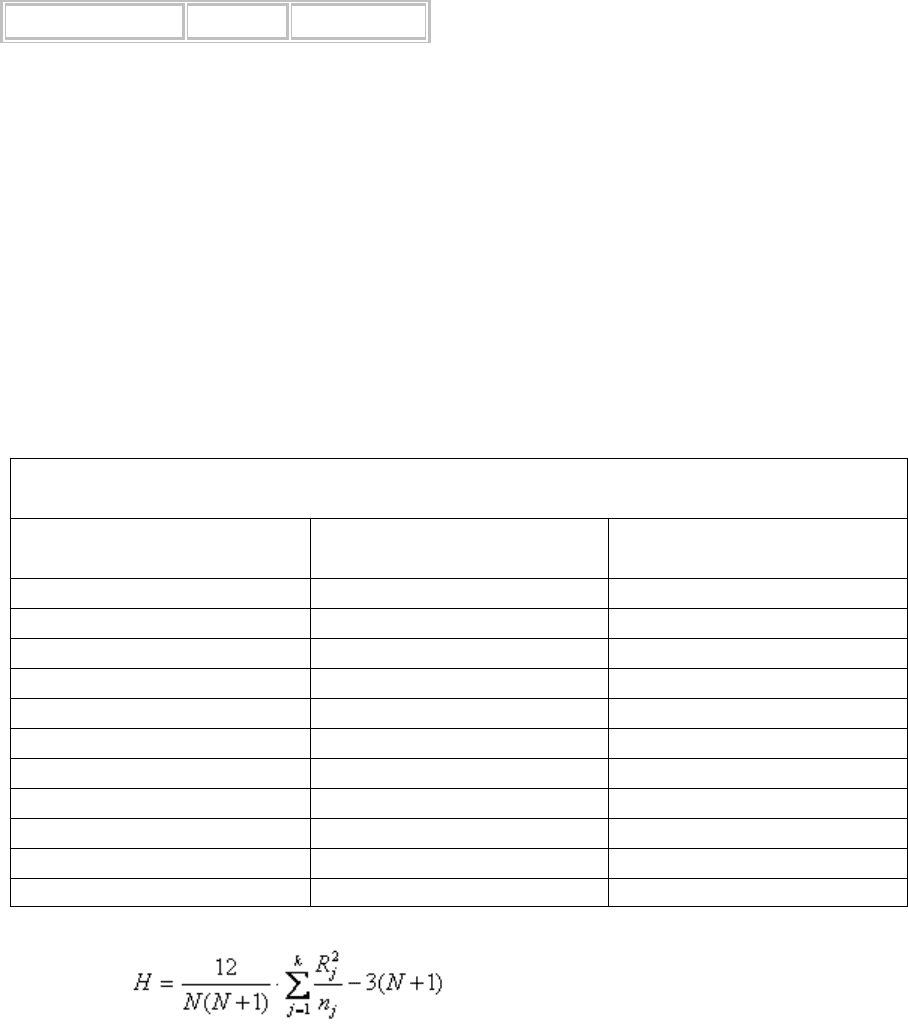
3). Рассчитаем статистку по формуле :
H=12/30/(30+1)*(96*96/10+166*166/10+203*203/10)-3*(30+1)=7,62
Н
кр
(α = 0.05)= 5,991
4) Для выявления значимых отличий правосторонний критерий ранговых сумм Уилксона
для двухвыборочных задач. Сравним попарно выборки «Первоисточник» - «Учебник» и
«Учебник» - «Компьютер».
5) Для сравнения проранжируем объединенные выборки и рассчитаем статистику W как
сумму рангов для методов «Учебник» в первом случае и «Компьютер» во втором.
6) Сформулируем гипотезы:
7
Н
0
: методы одинаково эффективны
Н
1
: изучение по учебнику эффективней изучения по первоисточнику, изучение с
помощью компьютерных программ эффективней изучения по учебнику
Первоисточник
28 1
Учебник
39 1
33 2 52 4
42 4 53 5
47 5 54 6
48 6 56 7,5
50 7,5 58 9
50 7,5 59 10
51 9 63 12,2
60 16 64 14,5
71 19 77 18,5
Учебник
39 3
Компьютер
41 2
52 10 49 3
53 11 56 7,5
54 12 62 11
56 13 63 12,2
58 14 64 14,5
59 15 65 16
63 17 72 17
64 18 77 18,5
77 20 87 20
133 121,7
Wкр(n=m=10, α = 0,05)=121,7
Для выборки «Первоисточник» - «Учебник»: W=133. W>Wкр. Так, гипотеза Н
0
принимается, значимых различий между изучением по первоисточнику и по учебнику нет.
Для выборки «Учебник» - «Компьютер»: W=121,7. W<Wкр. Так, гипотеза Н
0
принимается на уровне значимости 0,05, так как нет значимых различий между всеми
выборками, то статистически значимой тенденции возрастания показателей нет.
8
