Контрольная работа - Математические методы и модели в экономике (решение задач)
Подождите немного. Документ загружается.

Содержание
Условие задачи 6.3.....................................................................................................................2
Решение задачи 6.3....................................................................................................................3

Условие задачи 6.3
З а д а ч а 6 . 3 . Необходимо построить в регионе электростанцию большой
мощности. В данном регионе имеются возможности:
a
1
– построение большого водохранилища и гидроэлектростанции;
a
2
- сооружение тепловой электростанции на основном (газовом ) топливе и
резервном (мазуте);
a
3
– сооружение атомной электростанции.
Возможные решения
},,{
321
aaaA
. Экономическая эффективность каждого
варианта рассчитана проектным институтом, который учитывал затраты на строительство
и эксплуатационные расходы.
Случайные факторы, от которых зависит экономическая эффективность вариантов
капиталовложений, объединим в четыре возможных состояния природы -
)Θ,Θ,Θ,Θ(Ω
4321
- с учетом окупаемости:
1
Θ
- цены на газ и мазут низкие и климатические условия благоприятные;
2
Θ
- цены на газ и мазут высокие и климатические условия благоприятные;
3
Θ
- цены на газ и мазут низкие и климатические условия неблагоприятные;
4
Θ
- цены на газ и мазут высокие и климатические условия неблагоприятные;
Таблица 7.2
Ω
A
1
Θ
2
Θ
3
Θ
4
Θ
min
Гидроэлектростанция a
1
50 50 25 25 25
Тепловая
электростанция a
2
40 25 35 20 20
Атомная электростанция
a
3
30 30 30 30 30
max 50 50 35 30
Найти оптимальное решение для инвестирования средств
Решение задачи 6.3
Принятие решений в условиях неопределенности, как и в условиях
риска, требует определения альтернативных действий, которым
соответствуют платежи, зависящие от (случайных факторов) состояний
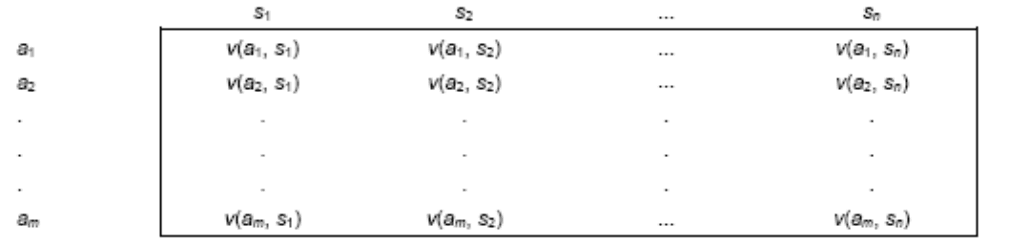
природы. Матрицу платежей в задаче принятия решений с m возможными
действиями и n состояниями природы можно представить следующим
образом:
Элемент a
i
представляет i-e возможное решение, а элемент s
j
— j-e
состояние природы. Плата (или доход), связанная с решением a
i
и состоянием
s
j
равна v(a
i
, s
j
).
Отличие между принятием решений в условиях риска и
неопределенности состоит в том, что в условиях неопределенности
вероятностное распределение, соответствующее состояниям s
j
, j = 1, 2, ..., n,
либо неизвестно, либо не может быть определено. Этот недостаток
информации обусловил развитие следующих критериев для анализа
ситуации, связанной с принятием решений.
1. Критерий Лапласа.
2. Минимаксный критерий (критерий Вальда).
3. Критерий Сэвиджа.
4. Критерий Гурвица.
Эти критерии отличаются по степени консерватизма, который
проявляет индивидуум, принимающий решение, перед лицом
неопределенности.
Критерий Лапласа опирается на принцип недостаточного основания,
который гласит, что, поскольку распределение вероятностей состояний Р(s
j
)

неизвестно, нет причин считать их различными. Следовательно, используется
оптимистическое предположение, что вероятности всех состояний природы
равны между собой, т.е. P{s
1
} = P{s
2
} = ... = P{s
n
} = 1/n. Если при этом v(a
i
, s
j
)
представляет получаемую прибыль, то наилучшим решением является то,
которое обеспечивает .
Если величина v(a
i
, s
j
) представляет расходы лица, принимающего
решение, то оператор "max" заменяется на ‘‘min’’.
Максиминный (минимаксный) критерий основан на консервативном
осторожном поведении лица, принимающего решение, и сводится к выбору
наилучшей альтернативы из наихудших. Если величина v(a
i
, s
j
) представляет
получаемую прибыль, то в соответствии с максиминным критерием в
качестве оптимального выбирается решение, обеспечивающее
.
Если величина v(a
i
, s
j
) представляет потери, используется минимаксный
критерий, который определяется следующим соотношением.
.
Критерий Сэвиджа стремится смягчить консерватизм минимаксного
(максиминного) критерия путем замены матрицы платежей (выигрышей или
проигрышей) v(a
i
,s
j
) матрицей потерь r(a
i
,s
j
), которая определяется
следующим образом.
Рассмотрим теперь критерий Гурвица. Этот критерий охватывает ряд
различных подходов к принятию решений — от наиболее оптимистичного до
наиболее пессимистичного (консервативного). Пусть 0 < α < 1 и величины

v(a
i
,s
j
) представляют доходы. Тогда решению, выбранному по критерию
Гурвица, соответствует
.
Параметр α — показатель оптимизма. Если α = 0, критерий Гурвица
становится консервативным, так как его применение эквивалентно
применению обычного минимаксного критерия. Если α =1, критерий Гурвица
становится слишком оптимистичным, ибо рассчитывает на наилучшие из
наилучших условий. Мы можем конкретизировать степень оптимизма (или
пессимизма) надлежащим выбором величины α из интервала [0, 1]. При
отсутствии ярко выраженной склонности к оптимизму или пессимизму
выбор α = 0,5 представляется наиболее разумным.
Если величины v(a
i
,s
j
) представляют потери, то критерий принимает
следующий вид:
.
Описанная ситуация в условии задачи 6.3 анализируется с точки зрения
четырех рассмотренных выше критериев.
Критерий Лапласа. При заданных вероятностях P{s
j
} = 1/4, j = 1, 2, 3, 4,
ожидаемые значения затрат (рассчитанных по условию задачи проектным
институтом) для различных возможных решений вычисляются следующим
образом.
M{a
1
} = (1/4)×(50 + 50 + 25 + 25) = 37,5,
M{a
2
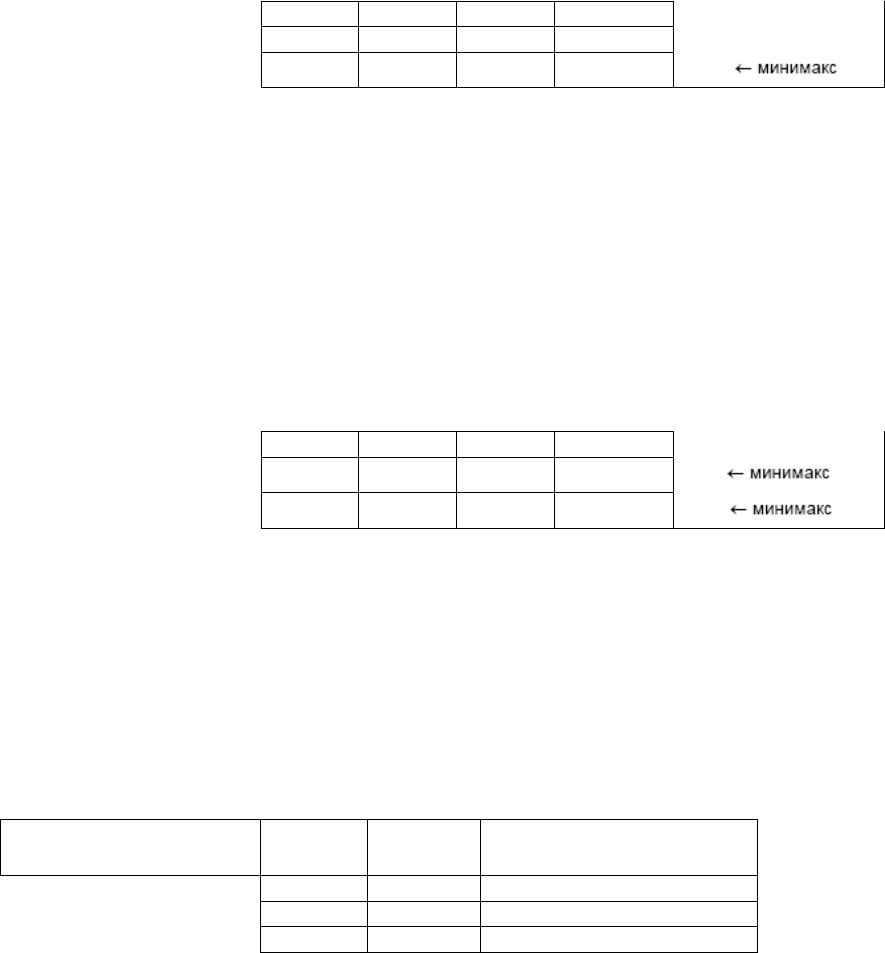
} = (1/4)×(40 + 25 + 35 + 20) = 30 ←Оптимум,
M{a
3
} = (1/4)×(30 + 30 + 30 + 30) = 30 ←Оптимум.
Таким образом согласно критерию Лапласа можно выбирать либо
стратегию (или решение) a
2
- сооружение тепловой электростанции на
основном (газовом) топливе и резервном (мазуте), либо a
3
- сооружение
атомной электростанции.
Выбрать однозначное решение мы не можем, т.к. M{a
2
} = M{a
3
}
←Оптимум.
Продолжим наше решение.
Минимаксный критерий. Этот критерий использует исходную матрицу.
s
1
s
2
s
3
s
4
Максимум строк
а
1
50 50 25 25 50
а
2
40 25 35 20 40
а
3
30 30 30 30
30
В соответствии с минимаксным критерием, предпочтительнее решение
a
3
- сооружение атомной электростанции.
Критерий Сэвиджа. Матрица потерь определяется посредством
вычитания чисел 50, 25, 30 из элементов столбцов от первого до третьего
соответственно (далее осуществляется «сдвижка» на 1-столбец и
анализируются столбцы со 2 по 4-ый). Следовательно, получаем
s
1
s
2
s
3
s
4
Максимум строк
а
1
0 25 -5
25
а
2
-10 0 5 5
а
3
-20 5 0 5
Можно выбирать либо стратегию (или решение) a
2
- сооружение
тепловой электростанции на основном (газовом) топливе и резервном
(мазуте), либо a
3
- сооружение атомной электростанции.
Критерий Гурвица. Результаты вычислений содержатся в следующей
таблице.
Альтернатива
Минимум
строк
Максимум
строк
α(минимум строки) + (1
– α)(максимум строки)
а
1
25 50 50-25α
а
2
20 40 40-20α
а
3
30 30 30
Используя подходящее значение для α, можно определить
оптимальную альтернативу. Например, при α = 0,5 оптимальными являются
либо альтернатива а
2
, либо а
3
, тогда как при α = 0,25 оптимальным является
решение а
3
.
При использовании 4 критериев стратегия a
2
выбиралась в качестве
оптимальной 3 раза, стратегия a
3
- 4 раза. Поэтому можно сделать вывод о
том, что применение стратегии a
3
- сооружение атомной электростанции
является более предпочтительным.
