Контрольная работа - Экономико-математические методы и модели (решение задач)

Подождите немного. Документ загружается.

Министерство образования Республики Беларусь

УО «Белорусский государственный экономический университет»

Кафедра

Контрольная работа

по курсу «Экономико-математические методы и модели»

Вариант №26

Минск 2009

СОДЕРЖАНИЕ

ЗАДАНИЕ 1.............................................................................................................2

ЗАДАНИЕ 2.............................................................................................................5

ЗАДАНИЕ 3.............................................................................................................8

ЗАДАНИЕ 4...........................................................................................................10

ЗАДАНИЕ 1

Для условной экономики, состоящей из двух отраслей, за отчетный период

известны межотраслевые потоки и вектор объемов конечного использования:

отч

пл

35 45 50 55

35 55 60 75

Рассчитать плановый межотраслевой баланс при условии, что в

плановом периоде конечное использование продукции задано вектором Yпл.

Привести числовую схему баланса.

Решение:

Рассчитаем валовой выпуск отраслей-производителей в отчетном

периоде (х

отч

) как сумму объемов промежуточного потребления (





) и

конечного использования (y

) их продукции:

отч1

= (35+45)+50 = 130

отч2

= (35+55)+60 = 150

Валовую добавленную стоимость (ВДС) отраслей-потребителей в

отчетном периоде определим как разность между валовым выпуском и

промежуточными затратами (





ВДС

= 130-(35+35) = 60

ВДС

= 150- (45+55) = 50

Составим матрицу коэффициентов прямых затрат (А), которая будет

характеризовать количество продукции i-той отрасли, необходимое для

производства единицы валовой продукции j-той отрасли. Элементы матрицы

рассчитаем по формуле

a 

= 35÷130 = 0,27 а

= 45÷150 = 0,3

= 35÷130 = 0,27 а

= 55÷150 = 0,37















0,370,27

0,30,27

Поскольку

YXA)(E 

, то искомый плановый валовой выпуск

отраслей возможно найти как

YA)(EX

1



где















;

BA)-(E

-1



- матрица коэффициентов полных затрат, характеризующая

количество продукции i-той отрасли, необходимое для производства

единицы конечной продукции j-той отрасли.

Рассчитаем элементы матрицы (Е-А):

































63,027,0

3,073,0

37,0127,00

3,0027,01

A)-(E

Затем составим обратную матрицу В = (Е-А)

-1

, используя формулу:















2212

2111

где Δ – определитель матрицы (Е-А).

Δ = 0,73×0,63 – (-0,27)×(-0,3) = 0,4599 – 0,081 = 0,3789

= (-1)

1+1

×0,63 = 0,63

= (-1)

2+1

×(-0,3) = 0,3

= (-1)

1+2

×(-0,27) = 0,27

= (-1)

2+2

×0,73 = 0,73































93,171,0

79,066,1

0,37890,730,37890,27

0,37890,30,37890,63



























































184

150

7593,15571,0

7579,05566,1

93,171,0

79,066,1

YВХ

Рассчитаем оставшиеся элементы модели планового межотраслевого

баланса:

jijij

xax 

= 0,27×150 = 41 х

= 0,3×150 = 45

= 0,27×184 = 50 х

= 0,37×184 = 68

ВДС

= 150-(41+50) = 59

ВДС

= 184-(45+68) = 71

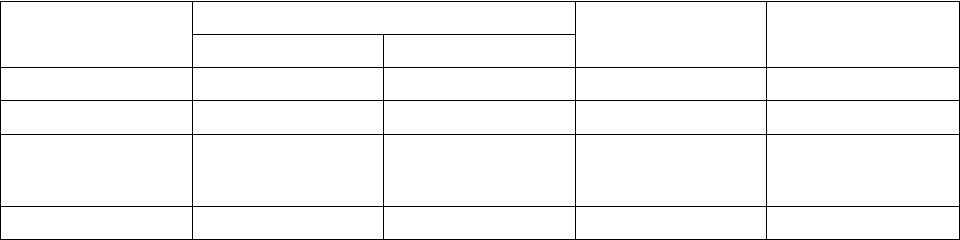
Составим числовую схему планового межотраслевого баланса:

пл

1 2

1 41 45 55 150

2 50 68 75 184

ВДС 59 71

130

пл

150 184

ЗАДАНИЕ 2

Определить оптимальную стратегию игрока А по всем критериям

(γ=0,6).

13 18 20 10

4 26 8 16

15 10 11 6

0,3 0,1 0,3 0,3

Решение:

Критерий Вальда – оптимальной принимается максиминная стратегия:

amin max α 

Определим максимин игры.

= min(13;18;20;10) = 10

= min(4;26;8;16) = 4

= min(15;10;11;6) = 6

Тогда α = max(10;4;6) = 10, следовательно оптимальна стратегия А

Критерий Сэвиджа – за оптимальную стратегию принимается та,

которая минимизирует максимальный риск:

r maxmin





Построим матрицу рисков:

2 8 0 6 8

11 0 12 0 12

0 16 9 10 16

Элементы матрицы r

определяются как разность между максимально

возможным выигрышем и выигрышем игрока при определенной стратегии

природы, т.е.:

ijijij

aamax r 

Максимальный выигрыш при стратегии природы П

будет равен 15.

Тогда r

= 15-13 = 2; r

= 15-4=11; r

=15-15=0. Аналогично определим

остальные элементы матрицы рисков.

Затем по матрице рисков находим максимальное значение r

риска при

пользовании игроком той или иной стратегией:

=8 ; r

=12; r

=16.

γ = min(8;12;16) = 8, следовательно оптимальна стратегия А

Критерий Лапласа - принимая состояния природы равновероятными



, за оптимальную стратегию принимается та, при которой

максимизируется средний выигрыш или минимизируется средний риск:





maxmax



или





minmin

Воспользуемся первой формулой, максимизирующей средний

выигрыш:

 

.А стратегии уетсоответств что 15,25,10,5) 13,5; max(15,25;

42) 54; (61;

max6111015 16;8264 10;201813

maxα





Критерий Байеса – если состояния природы известны q

(j=1...n; ∑q

=1),

то за оптимальную стратегию принимается та, при которой максимизируется

средний выигрыш или минимизируется средний риск:







jij

maxmax



или







jij

qrr

minmin

Воспользуемся первой формулой, максимизирующей средний

выигрыш при заданных вероятностях стратегий природы:

14,7 10,6) 11; max(14,7; 0,3)60,3110,1100,315

0,3;160,380,1260,34 0,3;100,3200,1180,3max(13α





Следовательно, оптимальной является стратегия А

Критерий Гурвица – за оптимальную стратегию принимается та,

которая максимизирует как минимальный, так и максимальный выигрыш при

определенном значении параметра γ.

10 ],aγ)max x (1amin max[δ

ijij





При заданном γ =0,6 получим:

148;9,6)max(14;12,15)0,4626;0,60,4420;0,60,410max(0,6δ 

Следовательно, оптимальной является стратегия А

Ответ: по всем исследованным критериям наиболее оптимальной для

игрока является стратегия А

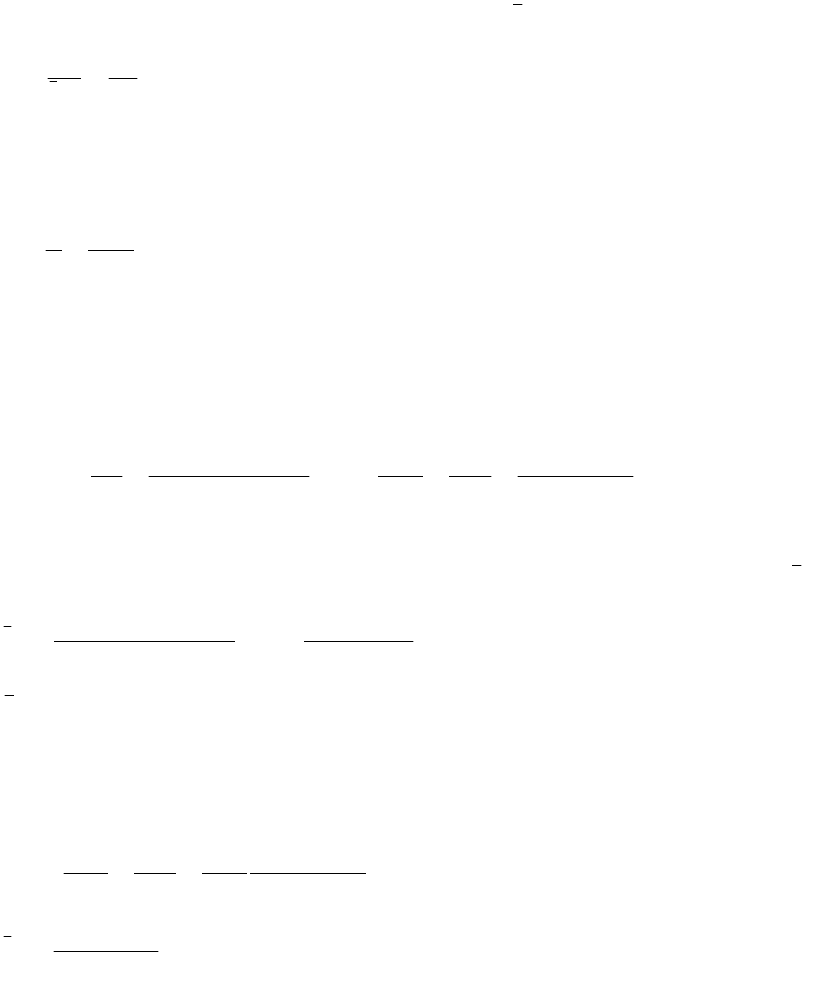
ЗАДАНИЕ 3

В магазин самообслуживания поступает пуассоновский поток

покупателей с интенсивностью 0,5 человек в минуту. Средняя

продолжительность расчета составляет 1,8 мин. Определить оптимальное

число контроллеров-кассиров, при котором время пребывания покупателей в

очереди не превышает 3 мин.

Решение:

Определим интенсивность выходного потока (μ) как величину,

обратную средней продолжительности расчета (

обс

56,0

8,1



обс



(мин.)

Далее рассчитаем интенсивность нагрузки системы (ρ), как частное

интенсивности входного (λ) и интенсивности выходного потоков:

0,9

0,56

0,5

ρ 

Воспользуемся методом подбора параметра. Примем количество

контроллеров-кассиров (n) равным 1. Тогда вероятность отсутствия

требований в системе (Р

) будет равна:

1,0)1,89,01(

)9,01(!0

9,0

)()!1(!

210



















































nnk

Затем найдем среднее время нахождения покупателей в очереди (

оч

160,1

0,010,56

0,9

)()!1(















оч

(мин.)

оч

>3, следовательно одного кассира для удовлетворения заданного

условия недостаточно.

Примем n=2 и повторим расчеты:

34,0)66,0405,09,01(

)9,02(!1

9,0

3210





















4,00,34

1,10,56

0,9







оч

(мин.)

Т.к.

оч

<3, то при n=2 заданное в условии задачи ограничение

выполняется.

Ответ: оптимальное число контроллеров-кассиров, при котором время

пребывания покупателей в очереди не будет превышать 3 мин., равно 2.