Кологривов В.А. Основы автоматизированного проектирования радиоэлектронных устройств
Подождите немного. Документ загружается.

31
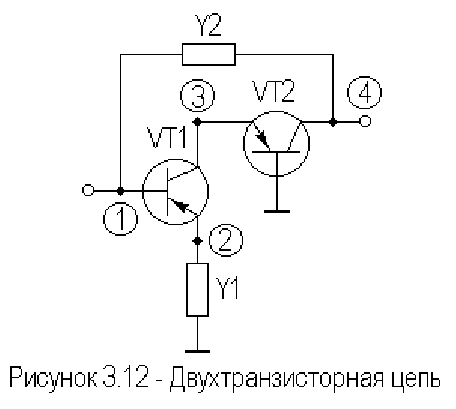
В качестве примера, рассмотрим формирование матрицы
проводимости схемы на двух транзисторах (рисунок 3
⋅12), заданных, в
свою очередь, подматрицами проводимости.
Выпишем матрицы проводимости компонент, включая двухполюсники
обратных связей, как подсхем
1
2
3
1
2
3
1
11 12 13
21 22 23
31 32 33
Y
yyy
yyy
yyy
VT
eee
eee
eee
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
'''
'''
'''
;
043
0
4
3
2
11 12 13
21 22 23
31 32 33
Y
yyy
yyy
yyy
VT
eee
eee
eee
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
'' '' ''
'' '' ''
'' '' ''
;
2
0
2
0
1
11
11
Y
yy
yy
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
;
14
1
4
2
22
22
Y
yy
yy
=
−
−
⎡
⎣
⎢
⎤
⎦
⎥
.
Здесь индекс
e - означает, что Y - параметры транзисторов измерялись в
одной схеме включения (схеме с ОЭ). Для получения матрицы
проводимости схемы достаточно свести подматрицы компонент в общую
матрицу, в соответствии с индексацией
1
2
34
1
2
3
4
0
0
11 2 1 3 12 2
31 33 1 32
21 23 22 33 32
223222
Y
yy y y y
yyyy
yyyyy
yyyy
=
+−
+
+
−+
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
'''
'' '
'''''''
'' ''
.
По поводу формирования матрицы проводимости схемы состоящей
из подсхем можно сделать следующие замечания:
1. Собственные проводимости объединенной матрицы равны сумме
собственных проводимостей подсхем подключенных к узлу.
2. Взаимные проводимости подсхем равны нулю в силу их
независимости.

32
3. Проводимости объединенной матрицы равны алгебраической
сумме соответствующих проводимостей подсхем.
В силу последнего замечания формирование матрицы проводимости
сложной схемы легко реализовать в виде универсального алгоритма.
3.3 Ме
тод контурных токов
Метод контурных токов, в силу ряда особенностей, не нашел
широкого применения при реализации программ машинного анализа
электрических схем, и представляет интерес разве что в теоретическом
плане. Прежде всего, это связано с некоторыми дополнительными
трудностями определения главных контуров в не планарных схемах.
Метод контурных токов применительно к машинным методам анализ
а
электрических цепей описан в [1] и в данном пособии не рассматривается.
3.4 Основные элемен
ты схемы
Базовыми элементами электрических цепей является линейные,
сосредоточенные и не зависящие от времени резисторы, конденсаторы и
катушки индуктивности.
Резистор - элемент, ток и напряжение которого связаны
соотношением
v
R
iiG
=
⋅
=
/
, (3.8)
где
R
- сопротивление
[
]
Om
;
G
- проводимость
[
]
Sim
;
v
- напряжение
[
]
V
; i - ток
[
]
A
. Различают линейные и нелинейные, зависящие от тока
или напряжения, резисторы.
Конденсатор - элемент, емкость которого обозначается
C
, единица
измерения
[
]
F . Описывается уравнением
q
f
v
=
(
)
, (3.9)
где
q - заряд
[
]
K
, либо
q
C
v
=
⋅
, (3.10)
для линейной постоянной емкости. Ток, протекающий через конденсатор
iqt
=
∂
∂
/
, (3.11)
Для линейной постоянной емкости
iC v t
=
⋅
∂
∂
/ , (3.12)
vv i d
C
t
=+⋅
∫
0
1
0
()
ττ
, (3.13)
где
v
0
- напряжение на конденсаторе, при
t
=
0
.
Индуктивность - элемент, обозначаемый
L
, единица измерения
[
]
H
n . Описывается уравнением
Φ
=
f
i
(
)
, (3.14)
где
Φ
- магнитный поток
[
]
Wb .

33
Напряжение на катушке индуктивности
vt
=
∂
∂
Φ
/ , (3.15)
Φ
=
⋅
L
i , (3.16)
vL i t
=
⋅
∂
∂
/ , (3.17)
ii v d
L
t
=+⋅
∫
0
1
0
()
ττ
, (3.18)
где
i
0
– ток, протекающий через катушку индуктивности, при
t
=
0
.
Уравнения, определяющие взаимосвязь токов и напряжений на
основных элементах, называются компонентными.
3.5 Преобразование Лапласа для у
равнений реактивных
элементов
Компонентные уравнения реактивных элементов (емкостей и
индуктивностей) описываются дифференциальными соотношениями. Для
линейных и постоянных элементов
L
и
C
компонентные уравнения, как
простейшие дифференциальные уравнения, преобразованием Лапласа
трансформируются в алгебраические уравнения и наоборот. В результате
соотношения из временного представления (относительно переменной
t
)
переводятся в комплексную плоскость переменной
s
j
=+
⋅
α
ω
. При
установившемся синусоидальном воздействии
sj f j
=
⋅
⋅⋅=⋅2
π
ω
.
Применяя преобразование Лапласа к уравнению (3.12)
iC v t
=
⋅
∂
∂
/
получаем
IsCVCV
=
⋅
⋅
−
⋅
0
. (3.20)
Преобразование Лапласа уравнения (3.17)
vL i t
=
⋅
∂
∂
/
,
дает
VsLILI
=
⋅
⋅
−
⋅
0
. (3.21)
При нулевых начальных условиях
V
0
0
=
и I
0
0
=
I
s
CV
=
⋅
⋅
; (3.22)
V
s
L
I
=
⋅
⋅
; (3.23)
откуда
YsC
C
=
⋅
; (3.24)
ZsL
L
=
⋅
; (3.25)
либо
ZsC
C
=
1 / ; (3.26)
YsL
L
=
1 / . (3.27)
Перепишем уравнения (3.20) и (3.21) в виде
ICV sCV
+
⋅
=
⋅
⋅
0
; (3.28)
VLI sLI
+
⋅
=
⋅
⋅
0
, (3.29)

34
здесь CV⋅
0
- источник тока, включенный параллельно
C
; LI⋅
0
- источник
напряжения, включенный последовательно с
L
. Можно также записать
уравнения (3.20) и (3.21) в виде
VV s sCI
−
=
⋅
0
1/(/); (3.30)
II s sLV
−
=
⋅
0
1/(/), (3.31)
где
Vs
0
/ - источник напряжения, включенный последовательно с
C
;
Is
0
/ - источник тока, включенный параллельно с
L
.
Рассмотренные представления удобно свести в таблицу 3.1.
Таблица 3.1 – Представление реактивн
ых элементов
Элемент
Проводимость Сопротивление
it C vt t() ()/=⋅
∂
∂
vt v i d
C
t
() ( )=+⋅
∫
0
1
0
ττ
IsCVCV
=
⋅
⋅
−
⋅
0
V
V
s
sC I−= ⋅
0
1(/ )
vL it t=⋅
∂
∂
()/
it i v d
L
t
(()0
0
1
0
=+⋅
∫
ττ
I
I
s
sL V−= ⋅
0
1(/ )
VsLILI=⋅ ⋅−
⋅
0
3.6 Нормировка входны
х данных
В реальных схемах часто наблюдается большой разброс значений
параметров. При решении уравнений описывающих подобные схемы
может возникнуть потеря точности при вычислениях и переполнение
разрядной сетки ЭВМ. Следует различать относительный и абсолютный
разбросы. Абсолютный разброс представляет собой отношение верхнего
предела номинала данного типа элемента к нижнему пределу.
Относительный разброс - это абсолютный разброс, нормированный на
среднегео
метрическое значение верхнего и нижнего номинала. Если
разброс симметричен относительно нуля, то абсолютный и относительный
разбросы совпадают, и нормировка ничего не дает. Однако часто разброс
35
несимметричен относительно нуля и нормировка позволяет существенно
повысить точность результатов и снизить вероятность переполнения
разрядной сетки.
В схемотехническом проектировании в качестве основных единиц
измерения используются: напряжение
U
V
[
]
, ток
I
A
[
]
, сопротивление
R
Om[
]
, емкость
C
F
[
]
, индуктивность
L
H
n
[
]
, частота F
H
z
[
]
, время
T
s
[
]
. Из семи возможных единиц только три могут быть независимыми,
причем не любые, а такие, чтобы остальные могли быть выражены через
них, в соответствии с соотношениями:
URITRCTRLF TZj L j C=
⋅
=⋅
=
=
=
⋅⋅=
⋅
⋅
;;/;/; /();11
ω
ω
где
ω
π
=⋅
⋅
2
F
.
В качестве комбинаций независимых единиц могут выступать,
например:
U
R
I
R
T
U
R
L
U
R
C
I
L
C
,, ; ,,; ,,; ,,; ,,
Ω
.
C другой стороны, в качестве комбинаций независимых единиц, не
могут выступать, например:
R
L
U
T
R
C
T
I
C
,, ; , ,; ,,; ,,
Ω
Ω
Ω
. Пусть
имеем параметр
x
и масштабный коэффициент M
x
, тогда нормированное
значение параметра
XxM
x
=
/
. Если наоборот, вычислен
нормированный параметр
X , тогда истинное значение параметра
xXM
x
=⋅ .
В качестве нормирующего множителя (масштабного коэффициента),
удобно брать, округленное до ближайшей степени десяти,
среднегеометрическое значение верхнего и нижнего пределов.
На практике часто в качестве независимых единиц выбирают:
U
R
U
R
L
U
R
C
,, ; ,,; ,,
Ω
. Очевидно, что вместо
U
, можно брать
I
, а
вместо
Ω
, можно брать
T
. Так, если комбинацией независимых единиц
является
(
,,
)
U
R
Ω
, то масштабные коэффициенты зависимых единиц
определятся как
MMMM MM MMM MM
IURT LR C R
=
=
=
=/; /; /; / /11
ΩΩ Ω
.
В качестве независимых единиц можно взять комбинацию с
меньшим числом единиц. В этом случае масштабные множители,
оставшихся независимых единиц подразумеваются равными единице. Так,
если в качестве независимой единицы взять Ω, то масштабные множители
остальных единиц равны
MM MM MM M
IUT L C
=
=
=
=
=1111 1;;; /; /
ΩΩ
.
В заключение отметим, что классические методы формирования
математических моделей отличаются относительной простотой и малой
размерностью, однако они не позволяют описывать схемы с произвольным
набором базовых элементов. Кроме того, классические методы не
позволяют напрямую переходить из частотной области во временную
область. От перечисленных недостатков свободны прямые методы
формирования математических моделей, базирующиеся на табличном
методе и его вариантах.
36
4 ПРЯМЫЕ МЕТОДЫ ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКИХ
МОДЕЛЕЙ
4.1 Табличны
й метод
Идея табличного метода заключается в объединении топологических
и компонентных уравнений цепи. В качестве топологических уравнений
используется уравнения для токов и напряжений ветвей, выраженные
через матрицу инциденций. При таком подходе все токи и напряжения
ветвей и напряжения узлов рассматривается, как неизвестные переменные.
Этот метод, очевидно, является наиболее общим, однако приводит к
сист
еме уравнений высокого порядка.
Допустим, что цепь имеет
b ветвей и n независимых узлов,
содержит
R
L
C
,, элементы, зависимые и независимые источники и
другие, часто используемые элементы. Топологические свойства цепи
можно отобразить матрицами инциденций
A
, сечений Q , и контуров
B
.
Т.к. матрица инциденций, в отличие от матриц сечений и контуров,
формируется непосредственно по схеме, именно она используется в
табличном методе. Уравнение Кирхгофа для токов, как известно,
запишется в виде
AI
b
⋅
=
0. (4.1)
Напряжения ветвей связаны с напряжениями узлов как
VAV
b
t
n
−⋅, (4.2)
где
VI
bb
, - напряжения и токи ветвей; V
n
- напряжения узлов.
Компонентные уравнения в самом общем случае могут быть
записаны как
токи
нап яжения
Y
K
V
K
Z
I
W
W
bb
b
b
р
1
2
1
2
1
2
⎡
⎣
⎢
⎤
⎦
⎥
⋅+
⎡
⎣
⎢
⎤
⎦
⎥
⋅=
⎡
⎣
⎢
⎤
⎦
⎥
,
где
YZ
12
, - соответственно проводимость и импеданс; KK
12
, –
безразмерные константы;
WW
bb12
, - токи и напряжения независимых
источников, в том числе источников, учитывающих влияние начальных
условий на конденсаторах и катушках индуктивности. Для компактности
воспользуемся более краткой формой компонентных уравнений
YV Z I W
bb bb b
⋅
+
⋅
=
. (4.3)
Заметим, что для различных типов ветвей
Y
b
и Z
b
могут принимать
конкретное значение: +1, -1, либо 0, а
W
b
- конкретное значение, либо 0.
В таблице 4.1 представлены значения
YZW
bbb
,, для некоторых
типов ветвей.
Таблица 4.1 – Комп
онентные уравнения двухполюсников
37
Элемент
Компонентные
уравнения
Y
b
Z
b
W
b
Резистор
VRI
bbb
−
⋅
=
0
1
−
R
b
0
Проводи-
мость
GV I
bb b
⋅
−
=
0 G
b
−1 0
Конденсатор
sC V I C V
bb b b
⋅⋅
−
=
⋅
0
sC
b
⋅
−1
CV
b
⋅
0
Катушка
инд-ти
VsLI LI
bbbb
−⋅
⋅
=
−
⋅
0
1
−
⋅sL
b
−
⋅
LI
b 0
Источник
напряж.
VE
bb
=
1 0
E
b
Источник
тока
IJ
bb
=
0 1
I
b
Заметим, что в таблице 4.1 конденсатор представлен как
проводимость
SC
b
⋅ , а индуктивность как сопротивление sL
b
⋅ .
В принципе, возможно и обратное представление, однако, забегая
вперед, можно отметить, что для формального перехода, от
алгебраических уравнений в частотной области к дифференциальным
уравнениям во временной области, недопустимы множители типа
1 /
s
.
Таким образом, это ограничение необходимо соблюдать, если на
основании математической модели предполагается вычисление временных
характеристик путем перехода от алгебраических уравнений к
дифференциальным уравнениям и их последующего интегрирования.
Табличную систему уравнений можно представить в виде
VAV
YV Z I W
AI
b
t
n
bb bb b
b
−⋅=
⋅+ ⋅=
⋅=
0
0
,
,
,
(4.4)
или в блочной матричной форме
bb n
b
b
n
A
YZ
A
V
I
V
W
t
bb
b
b
n
b
10
0
00
0
0
−
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⋅
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
, (4.5)
или в общем, виде
T
X
W
⋅
=
. (4.6)
Как следует из структуры уравнений, блочная матрица
T
имеет на главной
диагонали квадратные матрицы. При табличном методе нет оснований,
различать источники и пассивные компоненты, как в обобщенном узловом
методе. Нумерация элементов также может быть произвольной и лишь в
специальных теоретических исследованиях желательно иногда соблюдать
определенную нумерацию.
38
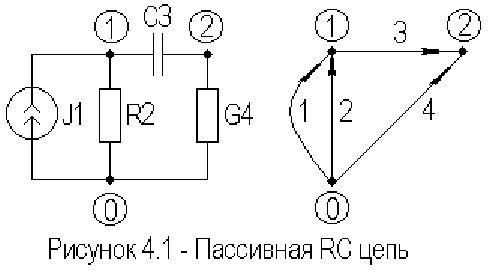
В качестве простейшего примера, рассмотрим цепь, изображенную
на рисунке 4.1.
Матрица инциденций схемы запишется
1
2
34
1
2
11 1 0
00 11
A =
−
−
⎡
⎣
⎢
⎤
⎦
⎥
.
Используя, матрицу инциденций схемы и таблицу 4.1 компонентных
уравнений ветвей, в соответствии с (4.5), получаем следующую табличную
систему
10 0 0 0 0 0 0 1 0
01 0 0 0 0 0 0 1 0
00 1 0 0 0 0 0 1 0
00 0 1 0 0 0 0 0 1
000 01 0 0000
01 0 0 0 0 0 0 0
00 0 0 0 10 0 0
00 0 0 0 0 1 0 0
00 0 0 1 1 1 0 0 0
00 0 0 0 0 1 1 0 0
2
3
4
1
2
3
−
−
−
−
⋅−
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⋅
R
sC
G
v
v
v
v
4
1
2
3
4
1
2
1
0
0
0
0
0
0
0
0
0
i
i
i
i
v
v
J
n
n
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
.
Если в начальный момент времени на емкости
C
3
есть напряжение V
0
, то
седьмой элемент вектора источников равен
wCV
730
=
⋅
.
В качестве достоинств табличного метода в сравнении с узловым
либо контурным методами, следует отметить возможность представления
более широкого набора типов ветвей, а такие возможность представления
некоторых ветвей, как в виде проводимости, так и в виде сопротивления.
В реальных схемах, кроме двухполюсных элементов, используются и
более сложные элементы, например управляемые источники активных
схем, поэтому расширим таблицу компонентных уравнений.
Таблиц
а 4.2 – Компонентные уравнения идеальных элементов
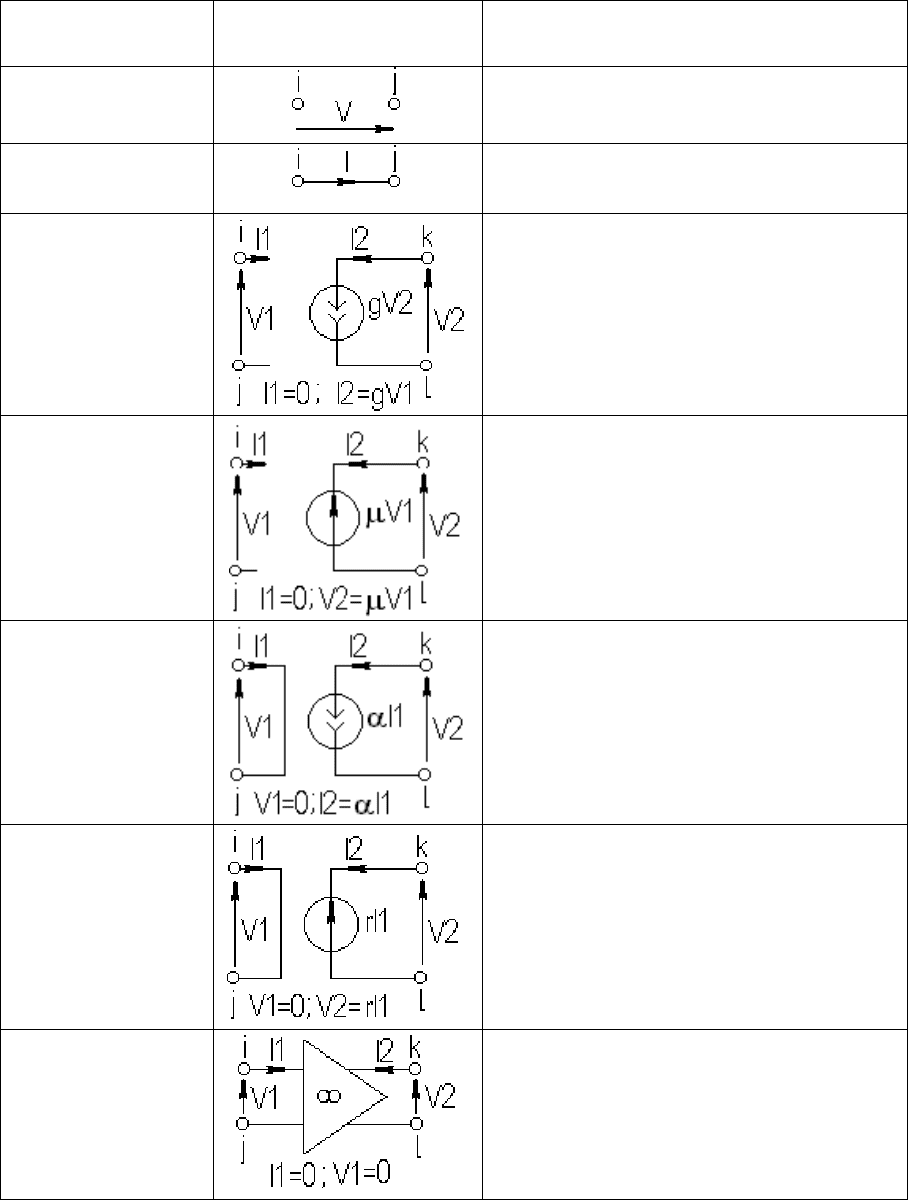
39
Элемент
Обозначение Компонентные
уравнения
Разомкнутая
цепь
I
= 0
Короткозамк.
цепь
V
= 0
Источник тока,
управляемый
напряжением
00
0
10
01
0
0
1
2
1
2
g
v
v
i
i
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
+
−
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
Источник
напряжения,
управляемый
напряжением
00
1
10
00
0
0
1
2
1
2
μ
−
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
+
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
v
v
i
i
Источник тока,
управляемый
током
10
00
00
1
0
0
1
2
1
2
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
+
−
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
v
v
i
i
α
Источник,
напряжения
управляемый
током
10
01
00
0
0
0
1
2
1
2
−
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
+
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
v
vr
i
i
Операционный
усилитель
10
00
00
10
0
0
1
2
1
2
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
+
⎡
⎣
⎢
⎤
⎦
⎥
⋅
⎡
⎣
⎢
⎤
⎦
⎥
=
⎡
⎣
⎢
⎤
⎦
⎥
v
v
i
i
Для иллюстрации табличного метода в качестве примера рассмотрим
схему рисунка 4.2, содержащую источник напряжения управляемый
напряжением.

40
Ввиду громоздкости табличной матрицы, запишем лишь матрицу
инциденций
A =
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
1 1 0 0 000
0 1 1 1 000
00 10110
00 0 1001
,
и компонентные уравнения рассматриваемой схемы
1
00
1
0
1
1
1
1
1
0
0
0
0
0
0
0
2
3
4
5
1
2
3
4
5
6
7
1
2
3
4
5
6
7
1
G
G
sC
sC
v
v
v
v
v
v
v
i
i
i
i
i
i
i
E
μ
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⋅
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
+
−
−
−
−
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⋅
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
.
Из примера видно, что коэффициенты табличной системы
получаются чрезвычайно разряженными. Дня сравнения различных
методов удобно ввести показатель заполнения
D = число ненулевых элементов/общее число элементов.
Для данного примера табличная система размерностью
1
8
1
8
⋅ имеет
39
ненулевых элементов. Следовательно,
D
=
=
39 1
8
12
2
/
% .
Недостаток табличного метода заключается в большом размере
систем уравнений и требовании специальных алгоритмов решения
разряженных систем уравнений. Причем структура уравнений такова, что
затрудняет использование более простых алгоритмов для разряженных
матриц с симметричной структурой.
4.2 Модификация та
бличного метода
