Колодий Н.А., Мазепа Е.А. Сборник задач и упражнений по теории вероятностей
Подождите немного. Документ загружается.


a ∈ R λ > 0
f(x) =
1
π
λ
λ
2
+ (x − a)
2
.
a
1
a
2
σ
2
1
σ
2
2
ρ a
1
, a
2
∈ R 0 < σ
1
, σ
2
< ∞
|ρ| ≤ 1
f
ξ
1
,ξ
2
(x
1
, x
2
) =
1
2πσ
1
σ
2
√
1−ρ
2
×
×e
−
1
2(1−ρ
2
)
(x
1
−a
1
)
2
σ
2
1
+
(x
2
−a
2
)
2
σ
2
2
−2ρ
x
1
−a
1
σ
1
x
2
−a
2
σ
2
.
n, p
1
, p
2
, . . . , p
s
n ∈ N 0 < p
1
, p
2
, . . . , p
s
< 1
s ∈ N
P
{ξ
1
= k
1
, ξ
2
= k
2
, . . . , ξ
s
= k
s
} =
n!
k
1
! k
2
! ···k
s
!
p
k
1
1
p
k
2
2
···p
k
s
s
,
0 ≤ k
1
, k
2
, . . . , k
s
≤ n,
s
X
i=1
k
i
= n.

α > 0
Γ(α) =
+∞
Z
0
t
α−1
e
−t
dt.
α
1
, α
2
> 0
B(α
1
, α
2
) =
1
Z
0
t
α
1
−1
(1 − t)
α
2
−1
dt.
Γ(α + 1) = αΓ(α);
Γ(n) = (n − 1)!;
Γ
n +
1
2
=
(2n−1)!!
2
n
√
π;
Γ
1
2
=
√
π;
Γ(x)Γ(1 − x) =
π
sin πx
0 < x < 1;
(α
1
, α
2
) =
Γ(α
1
)Γ(α
2
)
Γ(α
1
+α
2
)
.
I =
+∞
Z
0
e
−x
2
dx =
√
π
2
I
1
=
+∞
Z
0
e
−x
2
2
dx =
r
π
2
.
D(β) =
+∞
Z
0
sin βx
x
dx =
π
2
sign β.
L(α) =
+∞
Z
0
cos αx
1 + x
2
dx =
π
2
e
−|α|
.

A a N n
B b O o
C c P p
D d Q q
E e R r
F f S s
G g T t
H h U u
I i V v
J j W w
K k X x
L l Y y
M m Z z
A α N ν
B β Ξ ξ
Γ γ O o
∆ δ Π π
E ε P ρ
Z ζ Σ σ
H η T τ
Θ θ Υ υ
I ι Φ ϕ
K κ X χ
Λ λ Ψ ψ
M µ Ω ω
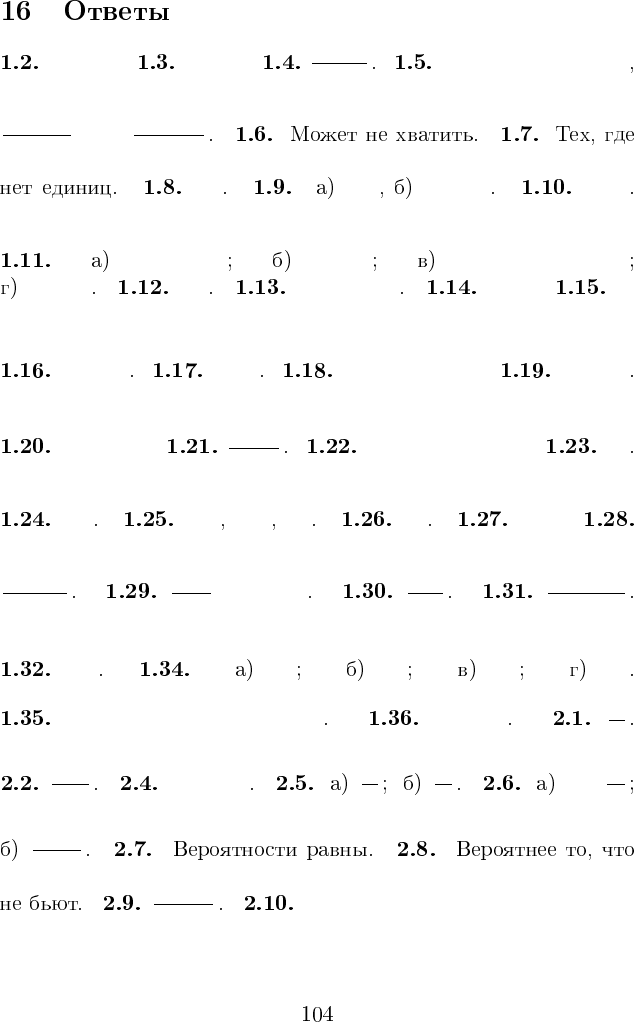
900000. 18000.
n(n−3)
2
(α
1
+1)·. . .·(α
n
+1)
p
α
1
+1
1
−1
p
1
−1
· ··· ·
p
α
n
+1
n
−1
p
n
−1
C
2
n
15 43200 2800
C
10
52
− C
10
48
4 · C
9
48
C
10
52
− C
10
48
− 4C
9
48
C
2
4
C
8
48
C
4
n
n
2
(n − 1)
2
7 · 7! 8!
(n−2)! (n!)
2
2(n−3)(n−2)! (n−1)!
n!(n−1)!
(n−1)!
2
n!−k!(n −k +1)! 2
n
2
10
120 120 30 20 265.
n!
k
1
!...k
m
!
10!
4!2!3!
= 12600
(28)!
(7!)
4
(n+m+s)!
m!n!s!
m
n
C
4
9
C
3
6
C
4
5
C
5
9
C
m−1
n
1
+m−1
C
m−1
n
2
+m−1
C
m−1
n
3
+m−1
C
n−1
n+k−2
5
36
1
6
n−1
A
7
10
10
−7
6!
6
6
6
6
6
1 −
5
n
6
n
n5
n−1
6
n
2
n−1
−1
2
n
−1
Ω = {(a
1
, . . . , a
k
)| 1 6 a
i
6 n, i =

1, k} |Ω| = n
k
Ω = {(b
1
, . . . , b
k+n−1
)| b
j
= 0, 1 Σ
j
b
j
= n − 1}
|Ω| = C
n−1
k+n−1
Ω = {(a
1
, . . . , a
k
)| 1 6 a
j
6 n; a
i
6= a
j
i 6= j} |Ω| = A
k
n
Ω = {{a
j
|j = 1, . . . , k}| 1 6 a
j
6 n; a
i
6= a
j
i 6= j} |Ω| = C
k
n
117
220
1
1+α
a
a+b
A
k
n
n
−k
a(a−1)+b(b−1)
(a+b)(a+b−1)
2ab
(a+b)(a+b−1)
(C
n
2n
)
2
/C
2n
4n
C
n
2n
2
−2n
25!
(5!)
5
5
25
1
C
4
19
n!
n
n
ad+bc
(a+b)(c+d)
C
k
K
C
n
N
C
m
M
C
k+n+m
K+N +M
(k+n+m)!
k!n!m!
K
k
N
n
M
m
(K + N + M )
−k−n−m
4!33!
36!
4!15·32!
36!
8
6
−13·7
5
8
6
4
133
C
3
40
37!
40!
C
m
n
2
n
C
n−m
n+k−m
C
n
n+k
2
C
n−1
2n−2
C
n
2n
2
C
n
2n−2
C
n
2n
24·10
4
·36!/40!
Σ
k
i=r
C
i
m
C
k−i
n−m
/C
k
n
Σ
r
i=0
C
i
m
C
k−i
n−m
/C
k
n
(9/10)
k
(9/10)
k
(8/10)
k
(2 · 9
k
− 8
k
)10
−k
8!/C
8
64
23
168
. 0, 079.
3
10
.
1
10
.
26/C
5
54
. R
6
R
2
R
3
A = A
2
∪ A
4
∪ A
6
B = A
3
∪ A
6
C = A
5
∪ A
6
D = A
2
∪ A
3
∪ A
5
∩
n
i=1
A
i
∪
n
i=1
A
i
∪
n
i=1
A
i
∩
j6=i
A
c
j
∪
16i
1
<i
2
<...<i
n−k
6n
A
c
i
1
. . . A
c
i
n−k

∪
16i
1
<i
2
<...<i
k
6n
A
i
1
. . . A
i
k
∪
(α
1
,α
2
,...,α
n
)
A
α
1
1
A
α
2
2
. . . A
α
n
n
α
i
∈ {0, 1} α
1
+ ··· + α
n
= k A
0
i
= A
i
A
1
i
= A
c
i
(∩
n
i=1
A
i
)∪(∩
n
i=1
A
c
i
) ∪
16i<j6n
(A
1i
∩A
2j
) ∪
j
i=1
A
1i
[−1; 1]
0 0
[−1;
−1
2
) ∪ (
1
2
; 1] A = A
16
A
36
A
c
46
∪ A
16
A
c
26
A
36
; B =
A
15
A
25
A
35
A
45
∪A
15
A
24
A
35
A
46
∪A
15
A
26
A
35
A
44
∪A
16
A
25
A
34
A
45
∪
A
14
A
25
A
36
A
45
; C = A
15
A
26
A
36
A
46
∪ A
16
A
26
A
35
A
46
∪
A
15
A
25
A
35
A
46
∪ A
15
A
26
A
35
A
45
∪ A
15
A
25
A
34
A
45
∪ A
14
A
25
A
35
A
45
.
a + b − 2p − q − r + 2h 1 − a − b − c + p + q + r − h
a + b − q − r − p + h
13
24
1
2
1
3
.
1
4
1
6
s+t
T
−
s
2
+t
2
2T
2
1
6
3
4
2
π
arcsin
r
R
2
π
arcsin
r
2R
1
2
1
3
1
3
.
2
3
−
√
3
2π
1
4
2
3
1
4
(1 −
r
a
)
2
3
4
√
2 − 1
1
4
1
4
3
4
1
2
1
2
π
8
1
4
8+π
48
0, 21
3
4
;
3
4

(l−3a)
2
l
2
l
3
6 a 6
l
2
1 − 3
(l−a)
2
l
2
l
2
6 a 6 l
1 −
19
20
2
1 −
180
200
2
19
27
8
51
1
3
1
4
α(1−β)(1−γ)
α(1−β)(1−γ)+(1−α)β(1−γ)+(1−α)(1−β)γ
p
1−(1−p)(1−q)
(1−p)q
1−(1−p)(1−q)
0
a+b
a+2b
83
210
43
210
2
5
291
2
9
Π
n
k=1
(1 − p
k
); 1 − Π
n
k=1
(1 − p
k
); Σ
n
k=1
p
k
Π
r6=k
(1 − p
r
)
P
(A) = 1 − (1 − p)
mn
P
(B) = (1 − (1 − p)
n
)
m
1 − (
3
4
)
3
1 −
r
3
R
3
N
1
2
(n+2)
2(n+1)
k
1
+n
1
·k
2
n
1
(n
2
+1)
k
1
k
1
+k
2
n
1
n
1
+m
1
+
k
2
k
1
+k
2
n
2
n
2
+m
2
1
3
(
p
1
1+p
1
+
p
2
1+p
2
+
p
3
1+p
3
)
N−2
N+M −2
P
(H
k
|A) =
2k
(n+1)n
k = 0, n
k
1
m
1
(m
2
+n
2
)
k
1
m
1
(m
2
+n
2
)+k
2
m
2
(m
1
+n
1
)
p
1
/(1+p
1
)
p
1
/(1+p
1
)+p
2
/(1+p
2
)+p
3
/(1+p
3
)
n
1
m
1
(n
2
+m
2
)(n
2
+m
2
−1)
n
1
m
1
(n
2
+m
2
)(n
2
+m
2
−1)+n
2
m
2
(n
1
+m
1
)(n
1
+m
1
−1)
2p
1+p−q
2(1−p−q)
1+p−q
P
(A) = 0;
P
(B) =
p;
P
(A \ B) = 0
1
1
2
1 c
1
+ c
2
= 1 F
ξ
(x) = 0 x < 0
1
8
0 6 x < 1
1
4
1 6 x < 2
3
8
2 6 x < 3
5
8
3 6 x < 4
3
4
4 6 x < 5
7
8
5 6 x < 6 1 x ≥ 6
F
ξ
(x) = 0 x < 0
7
8
0 6 x < 6 1 x ≥ 6.

c =
1
2
2−ln
2
2−2 ln 2
4
1 −
5
2e
1 c =
1
π
2
π
arctan 2
2
π
(arctan e − arctan e
−1
) 1 −
2
π
arctan e
−1
F (x) = 0
x < −1
(x+1)
2
2
x ∈ [−1, 0) 1 −
(1−x)
2
2
x ∈ [0, 1) 1
x ≥ 1 F (x) = 1 −
1
(1+x
2
)
2
x ≥ 0 0
e
−1
; e
−1
1
2
C
m
N
(
a
1
a
1
+a
2
)
m
(
a
2
a
1
+a
2
)
N−m
C
2
5
(
1
3
)
2
(
2
3
)
3
1
4
;
1
2
F (d−)−F (c−)
F (d−)−F (a)
f
ξ
(x) =
2
π
√
1−x
2
, x ∈ [0, 1]
M
ξ =
D
ξ = λ
M
ξ = np,
D
ξ = np(1 − p) = npq
P
{ξ = k} = C
k
20
3
5
k
2
5
20−k
, k = 0, 20; 12;
24
5
; 12
M
ξ = Σ
n
k=1
p
k
;
D
ξ = Σ
n
k=1
p
k
q
k
P
{ξ = k} =
P
{ξ = 14 −k} =
k−1
36
, k = 2, . . . , 6;
M
ξ = 7;
D
ξ =
35
6
N
6
1
λ
(1 −e
−λ
)
P
{ξ = k} = p(1 −p)
k
, k = 0, 1, . . . ;
M
ξ =
1−p
p
;
D
ξ =
1−p
p
2
c = 1;
M
ξ
2k+1
= 0;
M
ξ
2k
=
(2k)!
2
2k
c = 4;
M
ξ
n
=
(n+1)!
2
n
c = 2π
−1/2
;
M
ξ = π
−1/2
1/2;
√
2/2 0 f
ξ
(x) = 1/6, x ∈ [1, 7]
Mo ξ =
1
2
γ
1
= −
√
7
5
√
2
γ
2
=
18
155
0 0
Mo ξ = 0 Me ξ =
ln 2
λ
γ
1
=
2
λ
6
γ
2
=
9
λ
8
− 3
Mo ξ = 0 Me ξ = 0 γ
1
= 0 γ
2
< 0 Mo ξ = 0
Me ξ = 0 γ
1
= 0 γ
2
< 0 f
ξ
(x) =
1
2
sin x Mo ξ =
π
2
Me ξ =
π
2
γ
1
= 0 γ
2
≈ −1, 81 f
ξ
(x) = 1 −
1
x
5
x > 1 Mo ξ = 1 Me ξ =
5
√
2 γ
1
=
18
√
15
γ
2
≈ 73, 8

c =
6
π
2
F
ξ,η
(x, y) =
1
π
2
arctan
x
2
+
π
2
arctan
y
3
+
π
3
F
ξ
(x) =
1
π
arctan
x
2
+
π
2
F
η
(y) =
1
π
arctan
y
3
+
π
2
1
2
F
ξ,η
(x, y) =
sin x+sin y−sin (x+y)
2
x, y ∈
0,
π
2
1+sin y−cos y
2
x >
π
2
y ∈
0,
π
2
1+sin x−cos x
2
y >
π
2
x ∈
0,
π
2
1 x, y >
π
2
0 x, y < 0 F
ξ
(x) =
1+sin x−cos x
2
0 6 x 6
π
2
1 x >
π
2
0 x < 0; F
η
(y) =
1+sin y−cos y
2
0 6 y 6
π
2
1 y >
π
2
0 y < 0
P
(ξ >
π
4
, η <
π
2
) =
1
2
c = 1/2 f
ξ,η
(x, y) = cos x cos y x, y ∈
0,
π
2
x 6∈
0,
π
2
y 6∈
0,
π
2
1
2
f
ξ,η
(x, y) = 2
−x
3
−y
ln 2 ln 3
x > 0, y > 0, 0 x < 0 y < 0
41
54
p = 1
f
ξ,η
(x, y) =
1
4
x ∈ [2, 4], y ∈ [3, 5] 0 x 6∈ [2, 4]
y 6∈ [3, 5] F
ξ,η
(x, y) =
1
4
(x − 2)(y − 3) x ∈ [2, 4], y ∈ [3, 5]
1
2
(x−2) x ∈ [2, 4], y > 5,
1
2
(y −3) x > 4, y ∈ [3, 5] 1
x > 4, y > 5 0 x < 0 y < 0.
M
ξ =
2
3
R;
D
ξ =
R
2
18
P
{ξ = −1} = 0, 2
P
{ξ = 0} = 0, 35
P
{ξ = 1} = 0, 45
P
{η = 1} = 0, 8
P
{η = −1} = 0, 2
M
ξ
1
=
M
ξ
2
= 0;
D
ξ
1
=
D
ξ
2
= 1/2; cov(ξ
1
, ξ
2
) = 0
sign(a) −1 0
|ξ| >
1
2
, ξ
2
>
1
4
−
1
5
α
2
−β
2
α
2
+β
2
0
0 (σ
1
− σ
2
)
2
6
D
(ξ
1
+ ξ
2
) 6 (σ
1
+ σ
2
)
2
φ(ξ) =
1
2
ξ +
1
4
; a =
1
2
; b =
1
4
;
1
8
φ(ξ) = −
1
3
ξ; a =
−
1
3
; b = 0;
1
√
24
c =
1
√
2−1
; a = −0, 1133 . . . ; 0, 047 . . .
P
{η = −1} = F
ξ
(0−),
P
{η = 0} = F
ξ
(0) − F
ξ
(0−)

P
{η = 1} = 1 − F
ξ
(0);
M
η = 1 − F
ξ
(0) − F
ξ
(0−) G(x) =
0, x < 0, G(x) = F (x), x > 0
f
η
(y) = e
−y
, y > 0
f
η
(x) =
1
π
, x ∈ [−
π
2
,
π
2
] f
η
=
1
√
2πx
e
−x/2
P
(η =
−1) =
1
3
,
P
(η = 1) =
2
3
P
{η 6 x} = 1 − e
−λx
, x > 0
[0, 1] f
1/ξ
(y) =
b
π((1−ya)
2
+(yb)
2
)
y 6= 0 0 y = 0 f
η
(x) =
e
x
(1+e
x
)
2
f
η
(y) =
1
αy
1+α
α
y > 1 f
ξ
(y) =
1
2πa
, y ∈ [0, 2πa]
F
ξ
1
(x) F
T −ξ
2
(x)
[0, T ]
F
ξ
2
−ξ
1
(x) = 0 x < −T,
(T +x)
2
2T
2
x ∈ [−T, 0)
T
2
+2T x−x
2
2T
2
x ∈ [0, T ) 1 x > T
f
ξ
(x) =
1
2a
√
x
, x ∈ [0, a
2
] f
η
(x) = n
x
n−1
θ
n
x ∈ [0, θ]
M
η =
n
n+1
θ f
η
(x) = n
(1−x)
n−1
θ
n
x ∈ [0, θ]
M
η =
θ
n+1
f
ζ
(x) = 2λe
−2λx
x > 0
M
ζ =
1
2λ
f
ζ
(x) = 2λe
−2λx
(1 − e
−λx
)
x > 0
M
ζ =
3
2λ
1 − q
1
q
2
f
ξ
1
/ξ
2
(x) =
1
π(1+x
2
)
f(x) =
1
2
e
−
1
2
x
, x > 0 f(x) = xe
−x
2
/2
, x > 0
z
n
ψ
ξ
(z); ψ
ξ
(z
n
) p
0
= 1/4, p
1
= 1/2, p
2
= 1/4
p
k
=
1
k(k+1)
, k = 0, 1, . . . e
itb
φ
ξ
(at)
φ
ξ
(−t) |φ(t)|
2
e
it(a+b)
2
sin(t
b−a
2
)
t
b−a
2
