Кокуев А.Г. Решение задач оптимизации в среде MATLAB
Подождите немного. Документ загружается.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА «АВТОМАТИЗАЦИЯ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ»
РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В СРЕДЕ MATLAB
Методические указания к лабораторным
занятиям по курсу «Математические модели и
методы технической кибернетики» для
студентов специальностей 220301
«Автоматизация технологических процессов и
производств» и 220200 «Автоматизация и
управление»
Астрахань, 2009
2
Составитель:
Кокуев А. Г. – к.т.н., доцент кафедры «Автоматизация технологических
процессов»
Рецензент: д.т.н., проф. кафедры «Автоматизация технологических
процессов» Есауленко В.Н.
Решение задач оптимизации в среде MATLAB: метод. указания к
лабораторным занятиям по курсу «Математические модели и методы
технической кибернетики» для студентов специальностей 220301
«Автоматизация технологических процессов и производств» и 220200
«Автоматизация и управление»/ АГТУ; Сост.: А. Г. Кокуев.- Астрахань, 2009.-
29 с.
Указания содержат сведения, необходимые для изучения методов
одномерной минимизации. Приведена постановка задачи, рассмотрены
стратегии поиска экстремума функции одной переменной. Рассмотрены методы
равномерного поиска, деления интервала пополам, дихотомии, золотого
сечения.
Предназначены для студентов, обучающихся на втором курсе по
специальностям 220301 «Автоматизация технологических процессов и
производств» и 220200 «Автоматизация и управление»
Методические указания утверждены на заседании методического Совета
специальности 220301 «Автоматизация технологических процессов и
производств»
« ____ » ___________2009 г, протокол № ____.
3
Содержание
ВВЕДЕНИЕ ..................................................................................................... 4
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО ПОИСКУ
ОПТИМУМА .................................................................................................. 5
1.1 Постановка задачи и стратегии .......................................................... 5
1.2 Метод равномерного поиска .............................................................. 8
1.3 Метод деления интервала пополам..................................................... 9
1.4 Метод дихотомии ............................................................................... 12
1.5 Метод золотого сечения ..................................................................... 14
2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО РАБОТЕ В СРЕДЕ
MATLAB ....................................................................................................... 17
2.1 Рабочая среда MATLAB .................................................................... 17
2.2 Простейшие вычисления ................................................................... 19
2.3 Использование элементарных функций ........................................... 20
2.4 М-файлы .............................................................................................. 20
2.5 Работа в редакторе М-файлов ........................................................... 21
2.6 Управляющие конструкции языка программирования .................. 23
2.6.1 Операторы цикла ............................................................................. 23
2.6.2 Оператор ветвления if ..................................................................... 24
2.6.3 Прерывание и продолжение циклов .............................................. 25
2.7 Построение графиков в системе MATLAB ...................................... 25
2.7.1. Команда plot .................................................................................... 25
2.7.2. Разметка графика и надписи .......................................................... 26
2.7.3 Изображение функций .................................................................... 28
3. ЗАДАНИЕ И ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ ........................... 29
Задание ...................................................................................................... 29
Порядок выполнения работы .................................................................. 30
Содержание отчета ................................................................................... 30
4. СПИСОК ЛИТЕРАТУРЫ ........................................................................ 31

4
ВВЕДЕНИЕ
Проблема выбора оптимального варианта решения относится к числу
наиболее актуальных технико-экономических задач. В математической постановке
она представляет собой задачу минимизации (максимизации) некоторого
функционала, описывающего те или иные характеристики системы.
Численное решение оптимизационных задач на ЭВМ сводится к поиску
экстремума функции многих переменных. Таковы задачи оптимального управления
и идентификации, задача супервизорного управления, оптимального
проектирования и планирования.
Среди различных типов оптимизационных задач особое место занимают
задачи оптимизации невыпуклых детерминированных функций с единственной
точкой экстремума – так называемые унимодальные задачи.
Эти задачи представляют интерес с различных точек зрения. Прежде всего,
невыпуклость порождает большие аналитические сложности при разработке
методов решения унимодальных задач. Как известно, аналитические методы
развиты для значительно более простых задач.
Для линейных, квадратичных, выпуклых задач разработаны различные
численные методы решения, доказана сходимость методов, получены оценки
скорости сходимости.
На практике класс унимодальных задач не является чем-то необычным.
Имеются многочисленные примеры, когда в интересующей нас области
определения функции существует лишь один экстремум. Если при этом
оптимизируемая функция имеет сложный вид или задана неявно, ее выпуклость
ничем не гарантируется. В такой ситуации естественно применить метод
оптимизации, ориентированный на худший случай, т.е. на невыпуклость функции.
Разнообразие численных методов минимизации делает актуальным вопрос
об их сравнении. Невозможность строгого аналитического сравнения привела к
тому, что получило широкое распространение сравнение на тестовых примерах.
Установилась своеобразная культура такого сравнения — набор одних и тех же
тестов. Однако этот способ сравнения имеет и свои недостатки. Результаты
сравнения зависят от тестовой функции, от начальной точки процесса минимизации,
от размерности задачи. Непонятным остается сам факт, почему одни методы
оказываются более эффективными, чем другие.
Все это определяет актуальность сопоставительного исследования су-
ществующих численных методов минимизации применительно к классу
унимодальных задач.
5
1. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ПО ПОИСКУ ОПТИМУМА
1.1 Постановка задачи и стратегии
Постановка задачи
Требуется найти безусловный минимум функции f(x) одной переменной,
т.е. такую точку
Rx
*
, что
Rx
xfxf )(min)(
*
. Поставленная задача
одномерной минимизации может быть решена с помощью необходимых и
достаточных условий безусловного экстремума. Однако задача получения решения
уравнения
0
)(
dx
xdf
может оказаться весьма сложной. Более того, в практических
задачах функция f(x) может быть не задана в аналитическом виде или часто
неизвестно, является ли она дифференцируемой. Поэтому получение численного
решения поставленной задачи является актуальным.
Замечания:
1. Для методов одномерной минимизации типично задание априорной
информации о положении точки минимума с помощью начального интервала
неопределенности L
0
= [a
0
, b
0
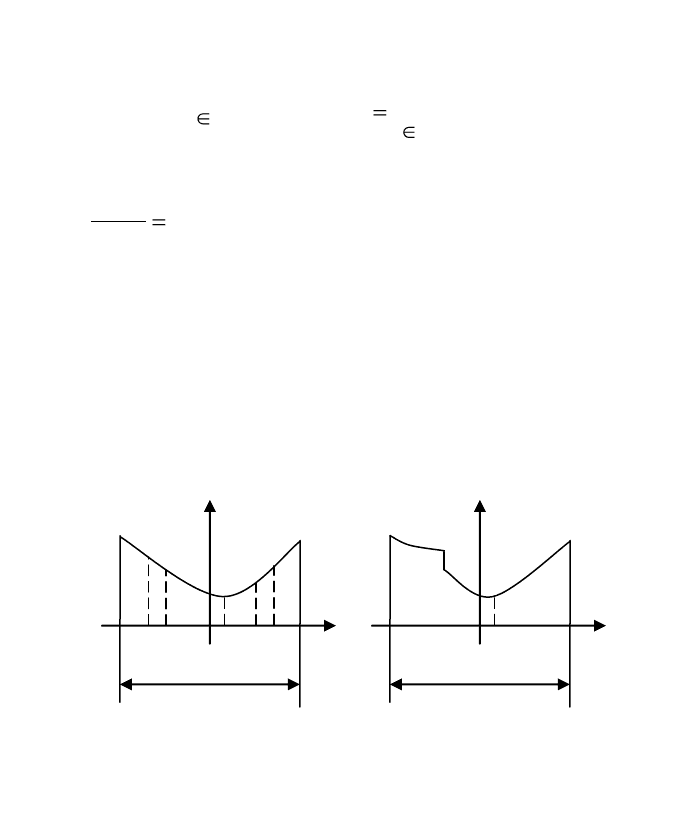
] (рис. 1.1). Предполагается, что точка минимума
x* принадлежит интервалу L
0
, но ее точное значение неизвестно.
2. Большинство известных методов одномерной минимизации применяется для
класса унимодальных функций.
а)
y
z
x*
y
z
f(x)
x
b
0
a
0
L
0
б)
x*
f(x)
x
b
0
a
0
L
0
Рис. 1.1 Интервалы унимодальных функций:
а) – непрерывной и выпуклой; б) – не являющейся непрерывной и выпуклой

6
Определение 1.1: Функция f(x) называется унимодальной на интервале
L
0
= [a
0
, b
0
], если она достигает глобального минимума на [a
0
, b
0
] в единственной
точке x*, причем слева от x* эта функция строго убывает, а справа от x* строго
возрастает. Если a
0
≤ y < z < x*, то f(y) > f(z), а если x* < y < z ≤ b
0
, то f(y) < f(z) (рис.
1.1 а).
Следует отметить, что непрерывная строго выпуклая функция является
унимодальной. Однако, определению 1.1 могут удовлетворять и функции, не
являющиеся непрерывными и выпуклыми (рис. 1.1 б).
Стратегии поиска
Существуют две принципиально различные стратегии выбора точек, в
которых производится вычисление значений функции. Если все точки задаются
заранее, до начала вычислений, — это пассивная (параллельная) стратегия. Если
эти точки выбираются последовательно в процессе поиска с учетом результатов
предыдущих вычислений, — это последовательная стратегия. Примером
реализации пассивной стратегии является метод равномерного поиска.
Последовательную стратегию можно реализовать следующими
способами:
применением квадратичной и кубической интерполяции, где по не-
скольким вычисленным значениям функции строится интерполяционный поли-
ном, а его минимум указывает на очередное приближение искомой точки экс-
тремума;
построением последовательности вложенных друг в друга интервалов,
каждый из которых содержит точку минимума.
Стратегия поиска включает в себя три этапа:
1. Выбор начального интервала неопределенности. Границы a
0
, b
0
ин-
тервала должны быть такими, чтобы функция f(x) была унимодальной.
2. Уменьшение интервала неопределенности.
3. Проверка условия окончания. Поиск заканчивается, когда длина теку-
щего интервала неопределенности [a
k
, b
k
] оказывается меньше установленной
величины.
Ответом является множество точек, принадлежащих последнему
интервалу неопределенности, среди которых каким-либо образом выбирается
решение задачи x*.
Замечания 1.1:
1. В некоторых методах заранее задается или находится количество N вы-
числений функции. В этом случае продолжительность поиска ограничена.
7
2. Для эвристического выбора начального интервала неопределенности
можно применить алгоритм Свенна [Swann W.H.]:
1) задать произвольно следующие параметры: x
0
— некоторую точку,
t > 0 — величину шага. Положить k = 0;
2) вычислить значение функции в трех точках: x
0
– t, x
0
, x
0
+ t;
3) проверить условие окончания:
если f(x
0
– t) ≥ f(x
0
) ≤ f(x
0
+ t), то начальный интервал неопре-
деленности найден: [a
0
, b
0
] = [x
0
– t, x
0
+ t];
если f(x
0
– t) ≤ f(x
0
) ≥ f(x
0
+ t), то функция не является унимодальной
(см. Определение 1.1), а требуемый интервал неопределенности не
может быть найден. Вычисления при этом прекращаются
(рекомендуется задать другую начальную точку x
0
);
если условие окончания не выполняется, то перейти к шагу 4);
4) определить величину Δ:
если f(x
0
– t) ≥ f(x
0
) ≥ f(x
0
+ t), то Δ = t, a
0
= x
0
, x
1
= x
0
+ t, k = 1;
если f(x
0
– t) ≤ f(x
0
) ≤ f(x
0
+ t), то Δ = -t, b
0
= x
0
, x
1
= x
0
- t, k = 1;
5) найти следующую точку x
k+1
= x
k
+2k
t
Δ;
6) проверить условие убывания функции:
если f(x
k+1
) < f(x
k
) и Δ = t, a
0
= x
k
;
если f(x
k+1
) < f(x
k
) и Δ =- t, b
0
= x
k
;
в обоих случаях положить k = k + 1 и перейти к шагу 5;
если f(x
k+1
) ≥ f(x
k
) процедура завершается. При Δ = t положить b
0
=
x
k+1
, а при Δ =- t положить a
0
= x
k+1
. В результате имеем [a
0
, b
0
] –
искомый начальный интервал неопределенности.
3. Уменьшение интервала неопределенности, осуществляемое при исполь-
зовании последовательной стратегии, производится на основании вычисления
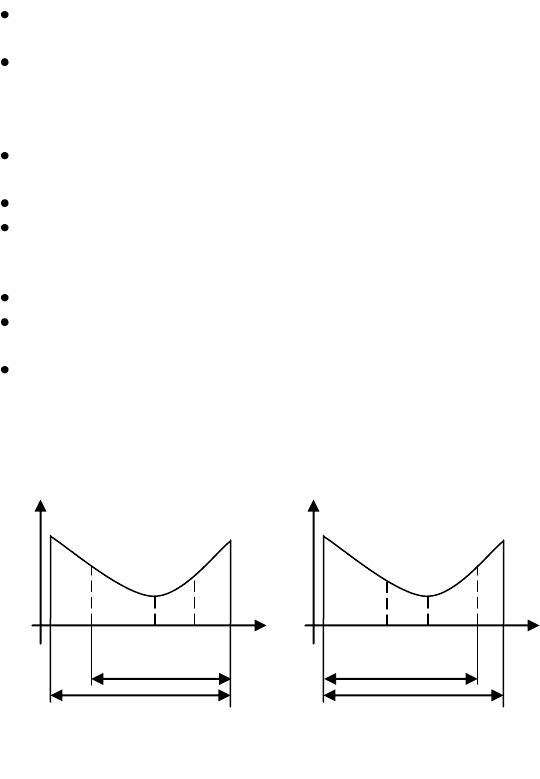
Рис. 1.2 Уменьшение интервала неопределенности
а)
б)
f(x)
x
новый интервал
y
x*
z
b
0
a
0
текущий интервал
f(x)
x
текущий интервал
новый интервал
y
x*
z
b
0
a
0
8
функции в двух точках текущего интервала. Свойство унимодальности
позволяет определить, в каком из возможных подынтервалов точка минимума
отсутствует.
Пусть в точках y и z интервала [a, b] вычислены значения функции: f(y)
и f(z). Если f(y) > f(z), то
),[
*
yax
и поэтому
],[
*
byx
(рис. 1.2, а). Если
f(y) < f(z), то
],(
*
bzx
и поэтому
],[
*
zax
(рис. 1.2, б). Иными словами, в
качестве нового интервала берется "гарантирующий интервал", наверняка
содержащий точку минимума. Если f(y) = f(z), в качестве нового интервала
можно взять любой из изображенных на рис. 1.2.
1.2 Метод равномерного поиска
Постановка задачи
Требуется найти безусловный минимум функции f(x) одной
переменной, т.е. такую точку
Rx
*
, что
Rx
xfxf )(min)(
*
.
Стратегия поиска
Метод относится к пассивным стратегиям. Задается начальный
интервал неопределенности L
0
= [a
0
, b
0
] и количество вычислений функции N.
Вычисления производятся в N равноотстоящих друг от друга точках (при этом
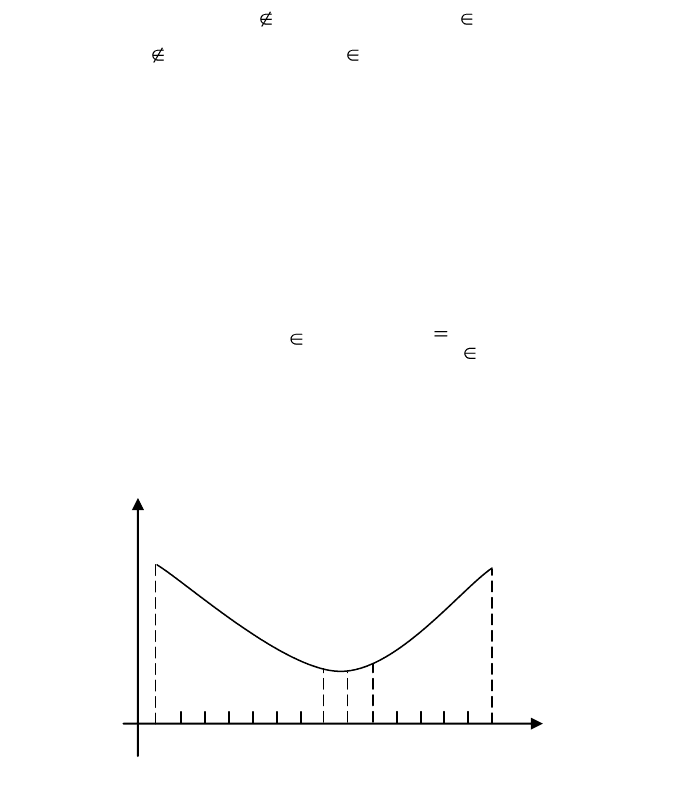
Рис. 1.3 Метод равномерного поиска
f(x)
x
x
1
x
k
x
N
b
0
a
0
x
k-1
x
k+1
x
2

9
интервал L
0
делится на N+1 равных интервалов). Путем сравнения величин f(x
i
),
i = 1,...,N находится точка х
k
, в которой значение функции наименьшее. Искомая
точка минимума х* считается заключенной в интервале [x
k-1
, x
k+1
] (рис. 1.3).
Алгоритм
Шаг 1. Задать начальный интервал неопределенности L
0
= [a
0
, b
0
] и
количество вычислений функции N.
Шаг 2. Вычислить точки
1
00
0
N
ab
iax
i
, i =1,...,N,
равноотстоящие друг от друга.
Шаг 3. Вычислить значения функции в N найденных точках: f(x
i
),
i =1,...,N.
Шаг 4. Среди точек x
i
, i =1,...,N, найти такую, в которой функция при-
нимает наименьшее значение:
Ni
xfxf
ik
1
)(min)(
.
Шаг 5. Точка минимума х* принадлежит интервалу [x
k-1
, x
k+1
], на
котором в качестве приближенного решения может быть выбрана точка х* ≈ x
k
Сходимость
Для метода равномерного поиска характеристика относительного
уменьшения начального интервала неопределенности находится по
формуле
1
2
)(
N
NR
, где N – количество вычислений функции.
Замечания 1.2:
Если задана величина R(N), то требуемое для достижения желаемой
точности количество вычислений функции определяется как наименьшее целое
число, удовлетворяющее условию
1
)(
2
NR
N
.
1.3 Метод деления интервала пополам
Постановка задачи
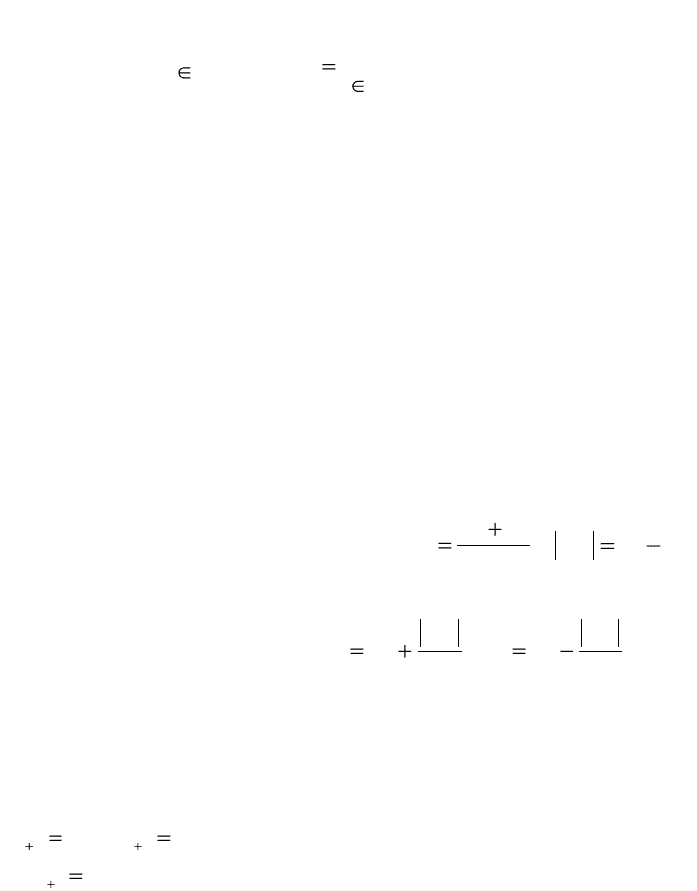
10
Требуется найти безусловный минимум функции f(x) одной переменной
т.е. такую точку
Rx
*
, что
Rx
xfxf )(min)(
*
.
Стратегия поиска
Метод относится к последовательным стратегиям и позволяет
исключить из дальнейшего рассмотрения на каждой итерации в точности
половину текущего интервала неопределенности. Задается начальный интервал
неопределенности, а алгоритм уменьшения интервала, являясь, как и в общем
случае, "гарантирующим" (см. рис. 1.2), основан на анализе величин функции в
трех точках, равномерно распределенных на текущем интервале (делящих его
на четыре равные части). Условия окончания процесса поиска стандартные:
поиск заканчивается, когда длина текущего интервала неопределенности
оказывается меньше установленной величины.
Алгоритм
Шаг 1. Задать начальный интервал неопределенности L
0
= [a
0
, b
0
] и l > 0
требуемую точность.
Шаг 2. Положить к = 0.
Шаг 3. Вычислить среднюю точку
2
kk
c
k
ba
x
,
kkk
abL
2
,
)(
c
k
xf
.
Шаг 4. Вычислить точки:
4
2k
kk
L
ay
,
4
2k
kk
L
az
и f(y
k
),
f(z
k
). Заметим, что точки
k
c
kk
zxy ,,
делят интервал [a
k
, b
k
] на четыре равные
части.
Шаг 5. Сравнить значения
)(
k
yf
и
)(
c
k
xf
:
а) если
)(
k
yf
<
)(
c
k
xf
, исключить интервал
],(
k
c
k
bx
, положив
c
kk
xb
1
,
kk
aa
1
. Средней точкой нового интервала становится точка
y
k
:
k
c
k
yx
1
. (рис. 1.4, а). Перейти к шагу 7;
