Ким Ч.В. Профилирование сопла с центральным телом
Подождите немного. Документ загружается.

Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1123
Профилирование сопла с центральным телом
Ким Ч.В (cwkim@mail.ru )
Московский физико-технический институт
Уравнения движения для стационарных изоэнтропических течений
идеального газа с произвольной термодинамикой могут быть представлены в
инвариантной форме, в которой уравнения термодинамического состояния
определяют лишь зависимости коэффициентов уравнений движения от
скорости и температуры торможения.
При этом в уравнениях можно совершить преобразование Чаплыгина в
плоскость годографа скорости. Преобразованные уравнения также
инвариантны относительно
уравнений состояния.
Поэтому, используя уравнения движения, инвариантные относительно
уравнений состояния, можно проектировать сопла с учётом зависимости
удельных теплоёмкостей от температуры.
Когда энтропия
cons
t
S
= , уравнения состояния задаются в виде :
∫
=
T
V
dTTCTE
0
)()( (1)
)()()(
T
T
T
p
ℜ
ρ= ,
∫
=ℜ
T
dT)T(R)T(
0
(2)
Несовершенный газ с уравнениями состояния (1, 2) определен как
«квази-совершенный». Зависимости
C
p
(T), C
v
(T) заданы формулами :
Теплоёмкость смеси :
C
p
, C
v
, k
p
C
1
= A
1
+ B
1
·
T
,
p
C
2
= A
2
+ B
2
·
T
,
p
C
3
= A
3
+ B
3
·
T
,
p
C
4
= A
4
+ B
4
·
T
· 0.37
p
C = y
1
·
p
C
1
+ y
2
·
p
C
2
+ y
3
·
p
C
3
+ y
4
·
p
C
4
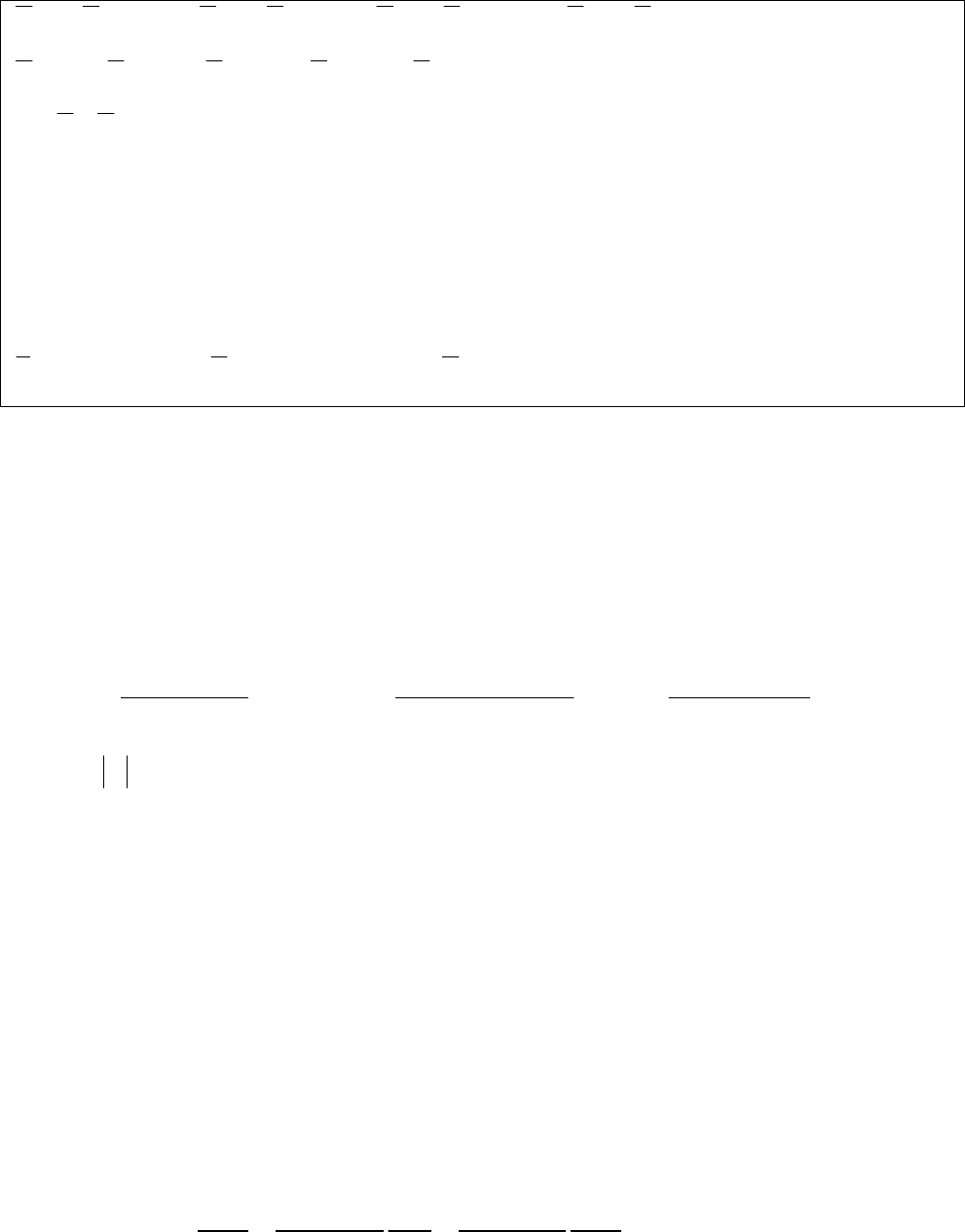
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1124
v
C
1
=
p
C
1
– 1,
v
C
2
=
p
C
2
– 1,
v
C
3
=
p
C
3
– 1,
v
C
4
=
p
C
4
- 1
v
C = y
1
·
v
C
1
+ y
2
·
v
C
2
+ y
3
·
v
C
3
+ y
4
·
v
C
4
k =
p
C /
v
C
A
1
= 5.30886
A
2
= 3.60820
A
3
= 3.78380
A
4
= 3.35202
B
1
= 0.29682
B
2
= 0.35166
B
3
= 0.11131
B
4
= 0.14020
y
1
= 0.1838
y
2
= 0.02
y
3
= 0.0102
y
4
= 0.786
T
= T/273 ºK
p
C
= C
p
/ R
o
v
C = C
v
/ R
o
R
o
=8.314 J/mole·K
Уравнения осесимметричного безвихревого течения идеального газа в
ортогональной системе координат (ψ,φ), связанной с линиями тока,
представлены в [1]. Обозначив
∫
ϕΛ−=Λ
ϕ
dMQ ))(ln1()(ln
2
, получим
окончательное представление уравнений движения
(
)
()
3030
0
2
30
1
h)T,(yQ
sin
ln
h)T,(Q
)T,(M
,)(ln
h)T,(Q
⋅
−
⋅
−
=
⋅
=
Λ
β
Λ
Λ
ΛΛ
βΛ
Λ
Λ
β
ϕ
ψψϕ
(3)
где
V=Λ , β- угол наклона вектора скорости по отношению к оси О, a
M
/
Λ
=
,
h
3
= 1, y для плоского и осесимметричного случаев соответственно.
Итак, уравнения стационарного изэнтропического движения
несовершенного газа инвариантны относительно уравнений состояния (1, 2).
В уравнениях (3) можно совершить преобразование Чаплыгина [2] в
плоскость годографа скорости точно так же, как и в уравнениях для
совершенного газа [3, 4], путём умножения якобианов (
∂( φ, ψ) /∂(Λ, β)).
Перекрёстно дифференцируя выражения φ
Λ
и φ
β
получим окончательное
уравнение для функции тока
Ψ(Λ, β) в несовершенном газе.
=
∂
∂−
+
∂
∂+
+
∂
∂
β
ψ
ΛΛ
ψ
ΛΛ
ψ
2
2
2
22
2
11 )M()M(
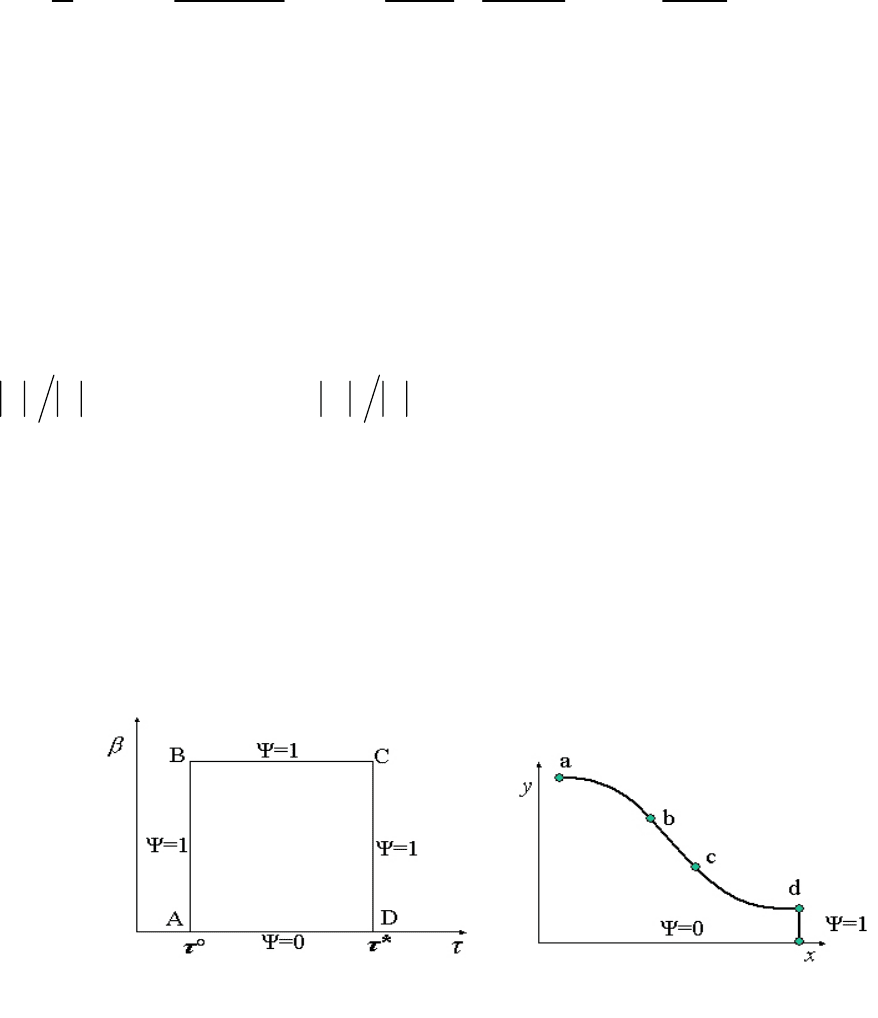
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1125
Рис. 2
Рис. 1
⎭
⎬
⎫
⎩
⎨
⎧
−+−
−
+
ββψβψΛψ
Λ
β
Ψ
Λ
β
Λ
β
Ψ
Λ
Ψ
D
y
sin
y
y
sin
y
cos
y
y
)M(
y
y
n
2222
2
2
2
2
211
(4)
где D =(
∂( φ, ψ) /∂(Λ, β)) и n = 0, 1 для плоского и осесимметричного случаев
соответственно.
В плоском течении при подстановке
)(),( ,
0
λ→
Λ
λ
→
Λ
qTQ система (3)
переходит в систему уравнений для совершенного газа. ( λ - коэффициент
скорости, газодинамическая функция )(
λ
q выражает удельный расход в
совершенном газе). В осесимметричном течении при соотношениях
τ =
22
max
VV
= Λ
2
/2C
p
T
o
, τ* =
22
max
VV
*
и Q
несовер
= Q
совер
ρ*/ ρ
o
уравнение (4)
переходит в обобщенное уравнение Чаплыгина для совершенного газа.
ДОЗВУКОВАЯ ЧАСТЬ СОПЛА
Корректная постановка задачи профилирования сопла Лаваля методом
годографа [4] не претерпевает никаких изменений в случае несовершенного
газа.
Прямоугольнику ABCD (Рис. 1) в плоскости годографа соответствует в
физической области контур сопла abcd (Рис. 2). Задача Дирихле в
прямоугольнике (Рис. 1) для уравнения (4) решена численным методом. После
решения для получения координат сопла
проводилось интегрирование вдоль
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1126
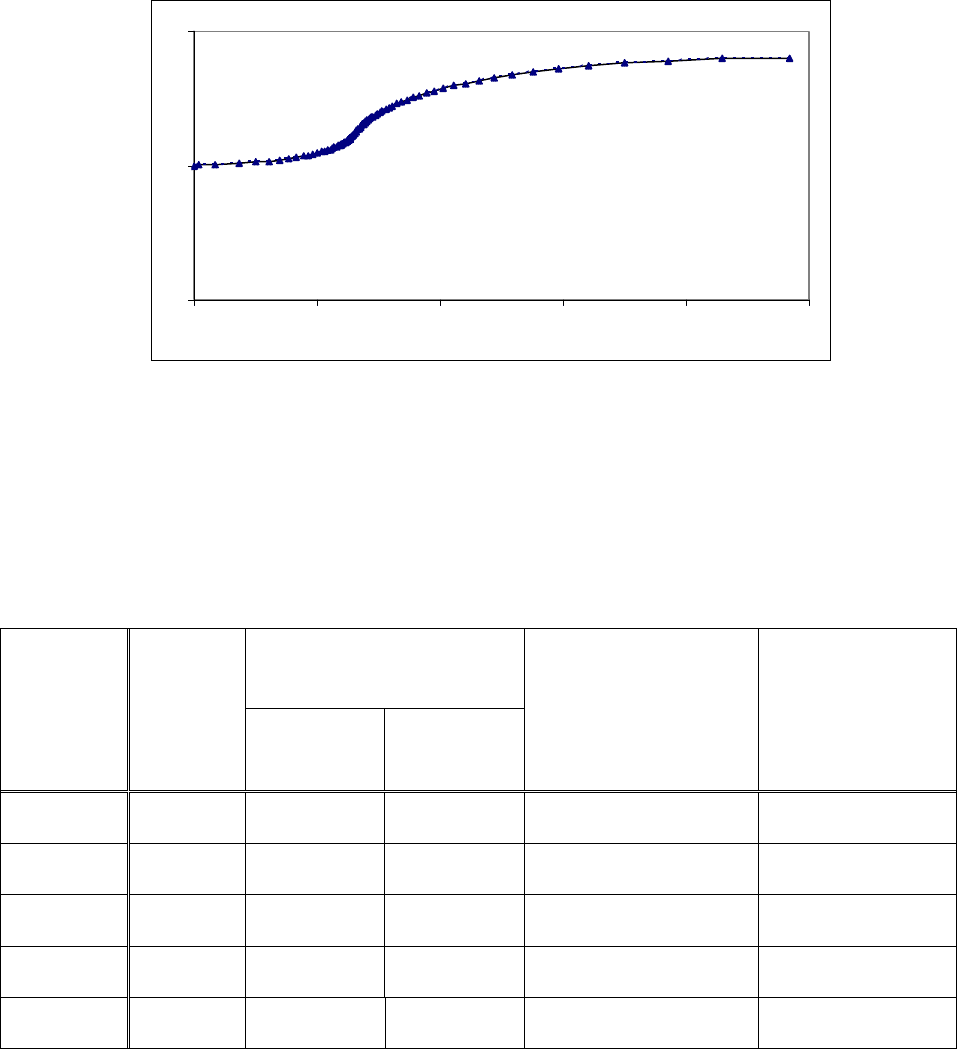
линий DC, CB и BA в плоскости годографа. Результаты расчётов представлены
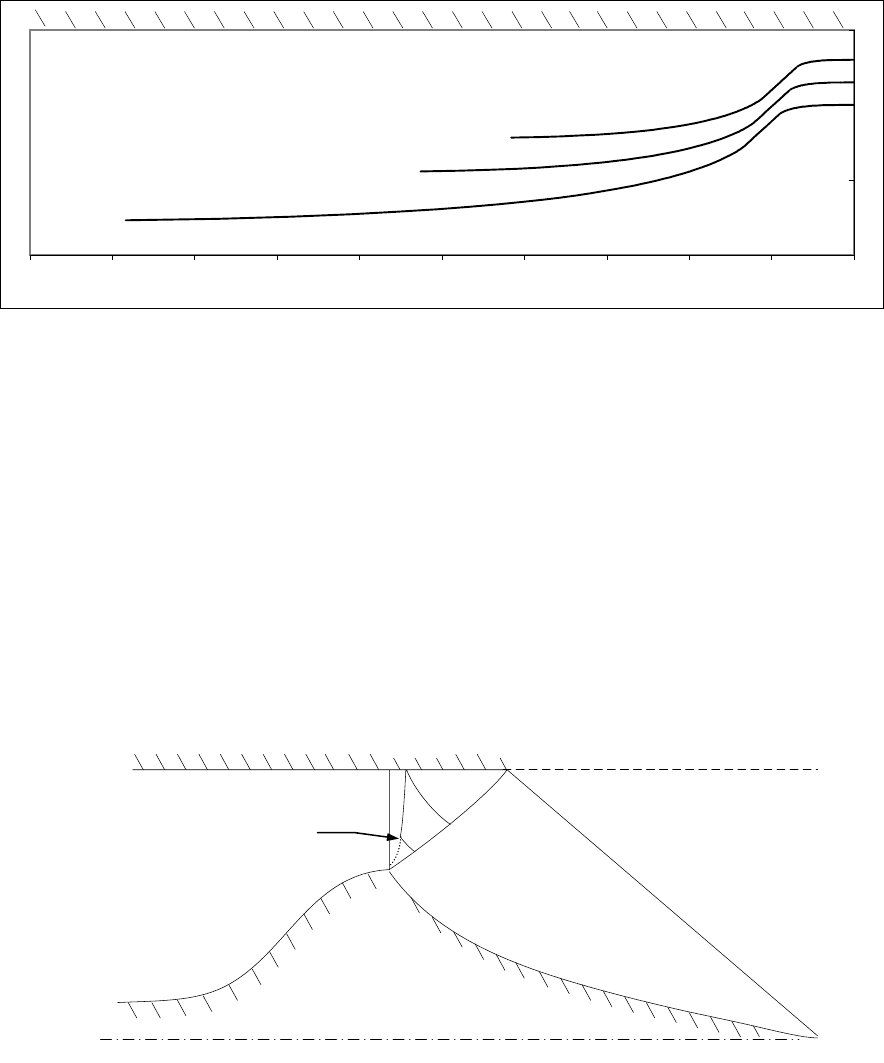
на рис. 3.
0
1
2
012345
На рис. 3. Контуры сопел для разной ширины щели в критическом
сечении при фиксированной наружной обечайке.
На рисунке сплошной линией показан контур, полученный при T
о
=
1000°K, пунктиром - при T
о
= 3000°K, а треугольником - при T
o
=5000 °K. Все
контуры почти совпадают.
скорость (m/s)
T
o
T*
на входе
на
выходе
соотношение
удельного
расхода
на входе и
выходе
соотношение
высоты
на входе и
выходе (h◦/h*)
1000 859.97 36.025 97.449 0.3462 1.8
2000 1745.14 50.631 137.066 0.3485 1.8
3000 2649.65 61.672 167.091 0.3499 1.8
4000 3569.30 70.893 192.177 0.3519 1.8
5000 4500.90 78.932 214.091 0.3530 1.8
Таб. 1
Поскольку величины теплоемкостей предполагаются зависящими от
температуры при проектировании сопел для горячих газов приходиться учесть
влияние температуры на теплоемкости. Однако как следует из
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1127
вышеизложенных результатов (Таб. 1), в дозвуковом течении изменение
теплоемкостей не приводит к значительному изменению контура.
0
1
2
3
-10-9-8-7-6-5-4-3-2-10
Рис. 4. Контур дозвуковой части осесимметричного сопла при T
о
= 3000°K.
Разные кривые соответствуют различным отрезкам звуковой линии.
СВЕРХЗВУКОВАЯ ЧАСТЬ СОПЛА
Схема вычисления течения для несовершенного газа не отличается от
схемы для совершенного газа [3], однако, алгоритмы на каждом этапе разные.
Сверхзвуковая часть контура в несовершенном газе вычисляется в четыре
этапа, как и в совершенном газе.
Рис. 5 Область определения течения в физической плоскости x, y.
A
E
A
′′
C
A
′
A
′
′
′
D
B
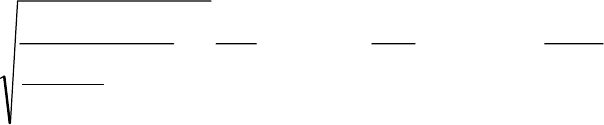
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1128
Алгоритмы вычисления характеристики первого семейства вблизи
звуковой линии не отличаются между решениями для несовершенного и
совершенного газа, поскольку для получения характеристику A
′′
A
′′′
(Рис. 5)
использовалось автомодельное решение уравнения Трикоми, инвариантного
относительно уравнений состояния [1].
На втором этапе возникают некоторые изменения от случая
совершенного газа в алгоритме вычисления характеристики второго семейства
A
′′
B в течении Прандтля-Майера вблизи угловой точки.
Используя условия совместности вдоль характеристики второго семейства
можно найти число Маха M
j
в точке с известным числом Маха M
j-1
предыдущей точки на характеристике. Число Маха M
j
должно удовлетворять
следующему уравнению.
0
11
1
1
2
1
=−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−
−
∫
−
θ
M
arcsin
M
arcsin
V
dV
)T(R
)T(C
)T(C
V
jj
V
V
v
p
j
j
(5)
где θ = (α
j-1
+ β
j-1
) – (α
j
+ β
j
), α – угол Маха. Уравнение (5) решается методом
проб и ошибок. При этом возникает трудности с выбором шага интегрирования.
По мере уменьшения шага интегрирования увеличивается точность, с другой
стороны объём вычислений значительно возрастает. Такая же трудность
возникнет при вычислении методом характеристик на каждом этапе. При
проведении расчёта в области A
′′′
A
′′
BD (между двумя характеристиками,
полученными на первых двух этапах) сначала вычисляется в
характеристическом четырехугольнике A
′′′
A
′′
BC, а затем в треугольнике A
′′′
CD,
ограниченном цилиндрической стенкой.
На третьем (вычисление решения в области A
′′′
A
′′
BD) и четвёртом этапах
(вычисление контура центрального тела – участка AE) расчёты проводились
методом характеристик с использованием следующих формул :

Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1129
(
)
(
)
()()
j,ij.ij,ij,i
j,ij,ij,ijj,ij,ij,ij,i
j,i
tgtg
xtgxtgyy
x
1111
11111111
−−−−
−−−−−−−−
++−
++−+−
=
βαβα
βαβα
(6)
(
)
(
)
j,ij,ij,ij,ij,ij,i
xxtgyy
1111 −−−−
−
++=
β
α
Вычисление числа Маха M
i,j
и угла наклона скорости β
i,j
в каждой точке
можно осуществлять двумя подходами.
Первый подход заключается в том, что методом проб и ошибок отыскать
значение V
i,j
, удовлетворяющее следующем уравнениям :
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−+−++=
∫∫
−−
−−
V
dV
)T(R
)T(C
)T(C
V
V
dV
)T(R
)T(C
)T(C
V
j,i
j,i
j,i
j,i
V
V
v
p
V
V
v
p
j,ij.ij,i
11
11
2
1
22
11
βββ
V
dV
)T(R
)T(C
)T(C
V
V
dV
)T(R
)T(C
)T(C
V
j,i
j,i
j,i
j,i
V
V
v
p
V
V
v
p
j,ij,i
∫∫
−−
−+−=−
−−
11
11
22
11
ββ
(7)
При решении двух уравнений основная погрешность в расчёте связана с
величинами шага V
i,j
, T
i,j
и шагов сеток.
Уменьшение шагов, которое производится с целью увеличения точности,
приводит к большей затрате времени. Поэтому при программировании для
численного решения учесть не только точность, но и быстродействующий
алгоритм.
Во втором подходе используется соотношение между касательной к
характеристике первого семейства, проходящей в плоскости (x, y) через одну
точку M и касательной
к характеристике второго семейства, проходящей через
соответствующую точку M' в плоскости (V
x
, V
y
), (ось параллельна оси V
x
).
При этом получается V
i,j
, решая уравнения V
x i,j
V
y i,j
:
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1130
21
1211121111
KK
)xx(Q)xx(QVxKVxKVyVy
Vx
j,ij,ij,ij,ij,ij,ij,ij,i
j,i
−
−−−+−+−
=
−−−−−−
ξξ
)xx(Q)VxVx(KVyVy
j,ij,ij,ij,ij,ij,i 12121 −−−
−
−
−−=
ξ
222
22
1
1
1
aVyVxaVxVy
aVx
y
K
'
C
−++
−
==
)aVy(y
yVya
Q
'
j,iC
2
1
2
11
11
2
1
1
2
−
=
−
(8)
222
22
2
2
1
aVyVxaVxVy
aVx
y
K
'
C
−+−
−
==
)aVy(y
yVya
Q
'
j,iC
2
2
2
22
12
2
2
2
1
−
=
−
,
где ξ = 0, 1 относятся к плоскому и осесимметричному случаям, а
индексы С
1
, С
2
- к характеристикам первого семейства и второго семейства
соответственно.
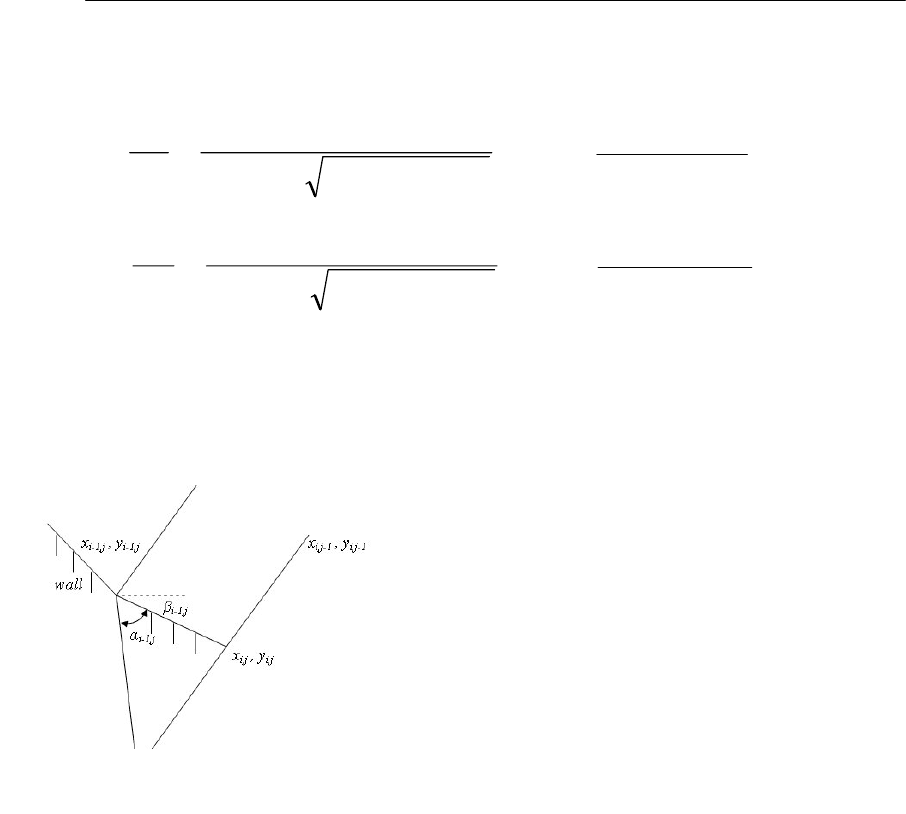
Координаты контура (x
i,j
, y
i,j
) центрального
тела могут быть получены вычислением
пересечения линии характеристики первого
семейства от точки x
i,j-1
, y
i,j-1
с линией (от
точки x
i-1,j
, y
i-1,j
) с углом наклона β
i-1,j
вектора
скорости относительно оси x.
Число Маха и угол наклона вектора скорости найдётся интерполяцией со
значениями М
i,j-1
, β
i,j-1
и М
*
, β
*
в точке x
*
, y
*
на линии воображённой
характеристики второго семейства от x
i-1,j
, y
i-1,j
(Рис. 6).
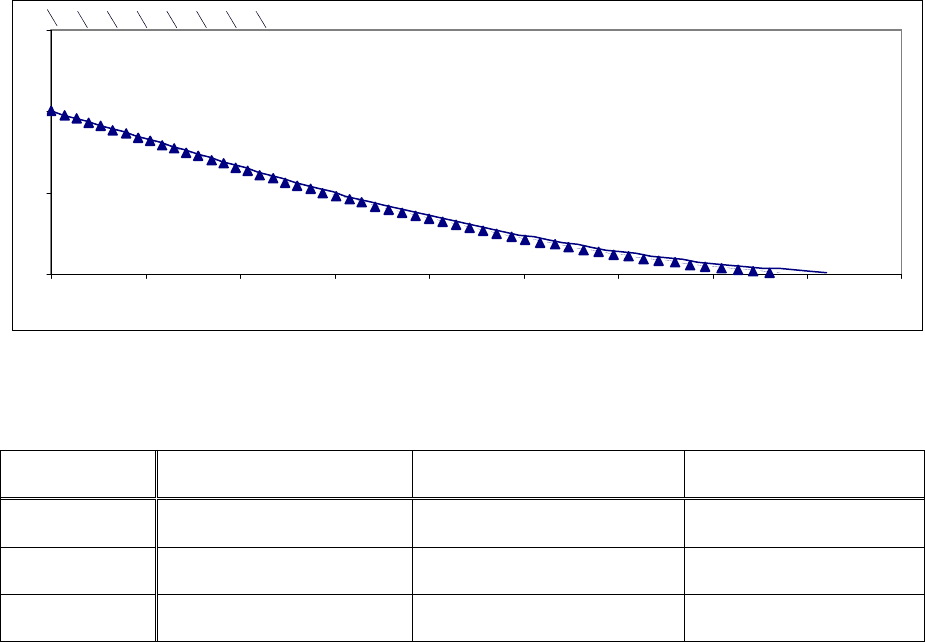
Теперь рассмотрим влияние температуры торможения на контур сопла.
На рис. 7 показаны результаты расчёта при разных температурах торможения.
В сверхзвуковой части сопла увеличение температуры торможения приведёт к
росту скорости на выходе сопла, а к уменьшению числа Маха.
Линией показан контур сопла при температуре торможения T
o
= 1000°K,
пунктиром - при T
o
=3000 °K, треугольником - при T
o
=5000 °K. В этих случаях
Рис. 6
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1131
скорости потока, скорости звука и число Маха на выходе сопла написаны в
таблице 2.
0
1
2
3
0123456789
Рис. 7. Контуры сверхзвуковой части осесимметричных сопел
с центральным телом.
T
o
скорость потока V
o
скорость звука a
o
число Маха M
o
1000 171.82 78.86 2.179
3000 299.82 140.41 2.135
5000 389.12 184.76 2.106
Таб. 2
Как показаны расчёты на рис. 7 и таб. 2, течение сверхзвуковой части
зависит от температуры торможения T
o
. Поэтому сопло, спроектированное под
какую-то температуру торможения, при её изменении окажется в нерасчётном
режиме. Иначе говоря, если сверхзвуковой часть оказывается короче, чем
нужно, то по теореме А.А.Никольского возникнет скачок уплотнения, что
приводит к дополнительным потерям [5].
Дальше проводилось сравнение контура для несовершенного газа с
контуром для совершенного газа.
Электронный журнал ИССЛЕДОВАНО В РОССИИ http://zhurnal.ape.relarn.ru/articles/2005/109.pdf
1132
0
1
2
3
012345678
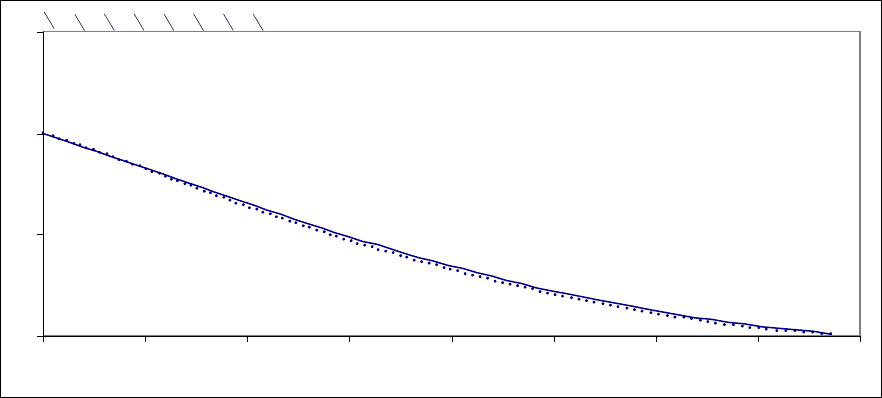
На рис. 8. Линией показан контур сопла при температуре торможения T
o
= 3000°K для несовершенного газа, пунктиром - для совершенного газа с
показателем адиабаты k = 1.3. В последнем случае число Маха на выходе сопла
состоится 2.062.
СПИСОК ЛИТЕРАТУРЫ
[1] Шифрин Э. Г. Потенциальные и вихревые трансзвуковые течения
идеального газа. М: Физматлит, 2001.
[2] Кочин Н. Е., Кибель И. А., Розе Н. В. Теоретическая гидромеханика, часть
вторая. Государственное издательство физико-математической литературы,
Москва 1963.
[3] Шифрин Э. Г, Ким Ч. В. Профилирование сопла с центральным телом
методом Чаплыгина. Доклады Академии Наук, Т. 401 №
1, 2005.
[4] Подсыпанина Н. А. Использование плоскости годографа при
профилировании численным методом осесимметричного сопла Лаваля. Изв.
АН СССР, МЖГ, № 1, 1977.
[5] Никольский А.А. О течениях газа вблизи остроконечных задних кромок тел
вращения. Сборник теоретических работ по аэродинамике, М., оборонгиз.
1957.
