Kelter P., Mosher M., Scott A. Chemistry. The Practical Science
Подождите немного. Документ загружается.


understanding to change these conditions to obtain the outcome I want?” Here are
some judgments we must make when we combine substances:
What chemical reactions will occur?
Which among these are important? Which are unimportant?
Given the initial concentrations of substances, in which direction
(toward the formation of more reactants or toward the formation of
more products) is the reaction likely to proceed?
How can we solve for the amounts of substances of interest that are
present at equilibrium?
How can we manipulate the conditions to maximize the concentra-
tion of the desired components and minimize that of the others?
A Case Study
We discussed the analysis of acetic acid (CH
3
COOH) previously. Here, we will
look at the equilibrium established when an acetic acid solution is prepared with
an initial concentration of 0.500 M. Remember the overarching question:
“Given
the chemical and physical conditions, how do I judge what is likely to happen?”
Specifically, what are the concentrations of all the substances in my flask at equi-
librium? Let’s approach this by answering the other questions, in order.
What chemical reactions will occur?
One reaction is the ionization of the acid as shown in reaction A, and this will
supply CH
3
COO
−
and H
+
. Another reaction that always occurs in aqueous solu-
tion is the ionization of water itself, also supplying H
+
, as shown in reaction B.
A: CH
3
COOH(aq)
CH
3
COO
−
(aq) + H
+
(aq) K = 1.8 × 10
−5
B: H
2
O(l)
H
+
(aq) + OH
−
(aq) K = 1.0 × 10
−14
Which among these are important? Which are unimportant?
The “important chemistry” is that which affects the outcome of the overall
process. The unimportant chemistry (in this context) is that which has no signif-
icant bearing on the outcome. The extent of the reactions and their relative
importance to us are indicated by their equilibrium constants. Even though nei-
ther reaction proceeds very far, the ionization of acetic acid is far more significant
than the ionization of water (we will test this assertion later.) We can make this
claim because the value of K for equation A is about 10
8
times larger than the
value of K for equation B. The mass-action expression for the ionization of acetic
acid (equation A) is
K =
[CH
3
COO
−
][H
+
]
[CH
3
COOH]
= 1.8 × 10
−5
In many systems, it is entirely possible that more than one reaction is impor-
tant to our calculations. However, in this chapter, we will typically deal with one
important reaction in each process that we discuss.
Given the initial concentrations of substances, in which direction is the
reaction likely to proceed?
We can predict the direction of change in a reaction by using the reaction quotient
(Q)
, which we introduced in Section 14.6. This is the numerical outcome of the
mass-action expression using initial concentrations, which are designated [ ]
0
.
Q =
[CH
3
COO
−
]
0
[H
+
]
0
[CH
3
COOH]
0
3
2
1
5
4
3
2
1
688 Chapter 16 Chemical Equilibrium
Video Lesson: Predicting the
Direction of a Reaction
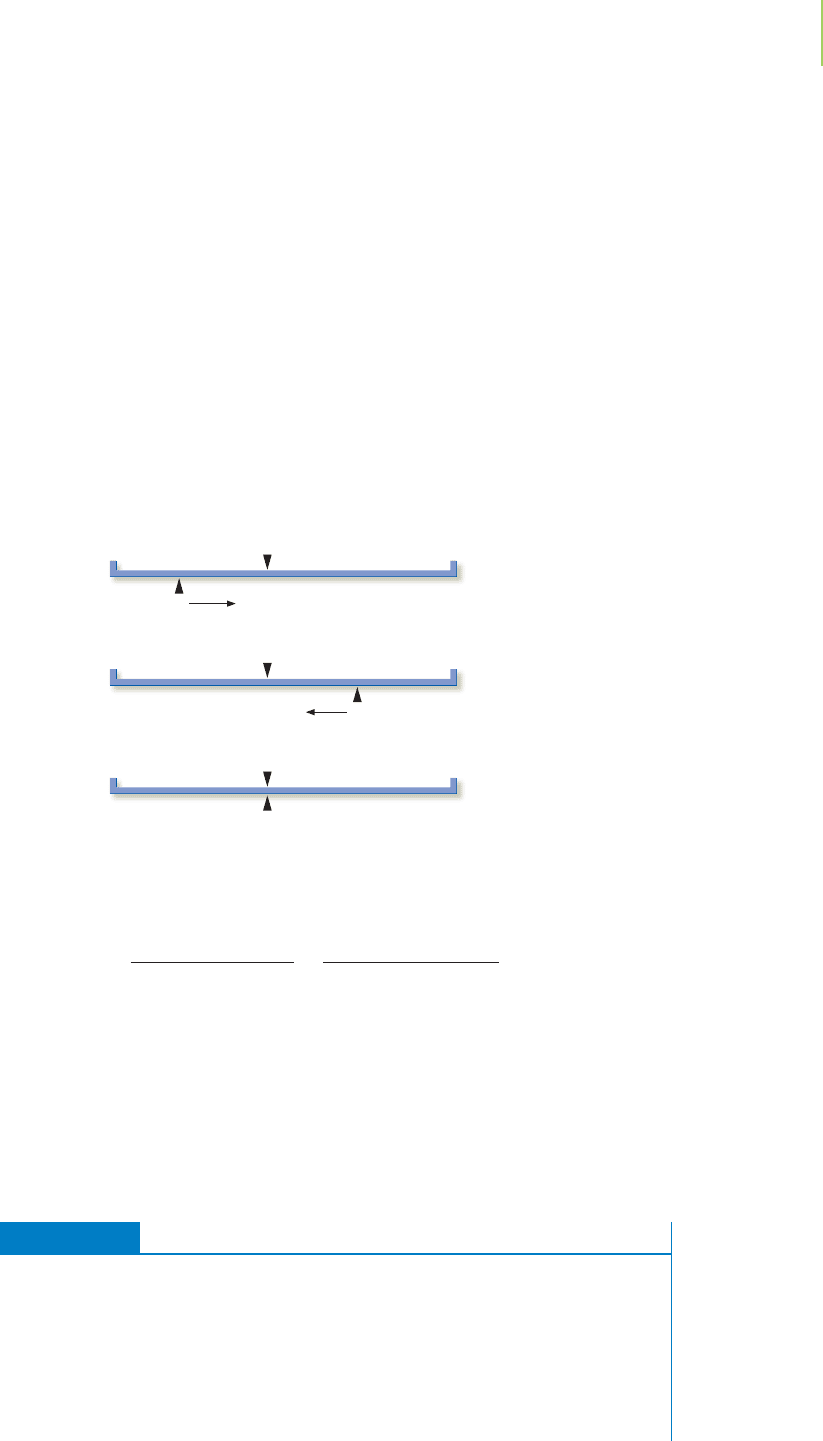
Q is then compared to the equilibrium constant, K, in order to determine the
direction in which the reaction will proceed. Keep in mind that Q deals with ini-
tial conditions and K deals with equilibrium conditions. Calculation of the reac-
tion quotient indicates which way the reaction will proceed in order to establish
equilibrium.
■
If Q is equal to K, the system is at equilibrium.
■
If Q is greater than K, there is too much product present. The system will shift
to the left to reach equilibrium. Mathematically, the numerator is much larger,
and the denominator much smaller, than the equilibrium values.
■
If Q is less than K, there is too much reactant present. The system will shift to
the right to reach equilibrium.
In our current example, the reaction must go toward formation of products (“to
the right”) because we initially have no products (Q =0), and this will be the case
in many equilibrium problems you will encounter.
If we were to change the initial concentration of our substances, such that
[H
+
]
0
= 0.0100 M,[CH
3
COO
−
]
0
= 0.200 M and [CH
3
COOH]
0
= 0.150 M,we
could calculate Q for these initial concentrations.
Q =
[CH
3
COO
−
]
0
[H
+
]
0
[CH
3
COOH]
0
=
(0.200 M)(0.0100 M)
(0.150 M)
= 0.0133
What does this value tell us? Q is much greater than K (1.8 × 10
−5
), so the reac-
tion will shift toward the formation of reactants (“to the left”). Mathematically,
this makes sense, because reducing the product concentration and increasing the
reactant concentration will reduce the quotient of the mass-action expression.
What does this indicate about the chemistry? If chemical change is an inevitable
part of our world, it is especially useful to be able to control that chemical
change in order to have a desirable impact on manufacturing, human biology,
and the environment.
EXERCISE 16.7 Predicting the Direction of Equilibrium
Predict the direction in which the reaction of myoglobin and oxygen will proceed to
reach equilibrium for each set of conditions.
Mb + O
2
MbO
2
K = 8.6 × 10
5
a. Q = 1500
b. Q = 8.3 × 10
6
c. [Mb]
0
= 2.04 × 10
−4
M;[O
2
]
0
= 3.00 × 10
−6
M; [MbO
2
]
0
= 2.50 × 10
−4
M
16.5 Solving Equilibrium Problems—A Different Way of Thinking 689
Reactants
Q
E
Products
When
Q <
K
Reactants
Q
Products
Q >
K
Reactants
Q
Products
Q =
K
E
E
Solution
a. Q < K, so the reaction will form more products and shift to the right.
b. Q > K, so the reaction will form more reactants and shift to the left.
c. Q =
[MbO
2
]
0
[Mb]
0
[O
2
]
0
=
[2.50 ×10
−4
]
[2.04 ×10
−4
][3.00 ×10
−6
]
= 4.08 ×10
5
Q < K, so the reaction will form more products and shift to the right.
d. Q =
[1.00 ×10
−4
]
[5.00 ×10
−5
][9.21 ×10
−7
]
= 2.17 × 10
6
Q > K, so the reaction will form more reactants and shift to the left.
e. Q =
[1.94 ×10
−4
]
[1.0 ×10
−4
][2.25 ×10
−6
]
= 8.6 × 10
5
Q = K, so the reaction is at equilibrium.
Further Insights
Food for thought: How might these shifts in the direction of the reaction toward
equilibrium allow the muscles in the body to obtain needed oxygen during vigorous
exercise?
PRACTICE 16.7
Under certain specific conditions, the formation of ozone from NO
2
has an equilib-
rium constant K = 120. Predict the direction of the following reaction, given the
conditions in each case below.
NO
2
(g) + O
2
(g)
NO(g) + O
3
(g) K = 120
690 Chapter 16 Chemical Equilibrium
d. [Mb]
0
= 5.00 × 10
−5
M;[O
2
]
0
= 9.21 × 10
−7
M; [MbO
2
]
0
= 1.00 × 10
−4
M
e. [Mb]
0
= 1.0 × 10
−4
M;[O
2
]
0
= 2.25 × 10
−6
M; [MbO
2
]
0
= 1.94 × 10
−4
M
First Thoughts
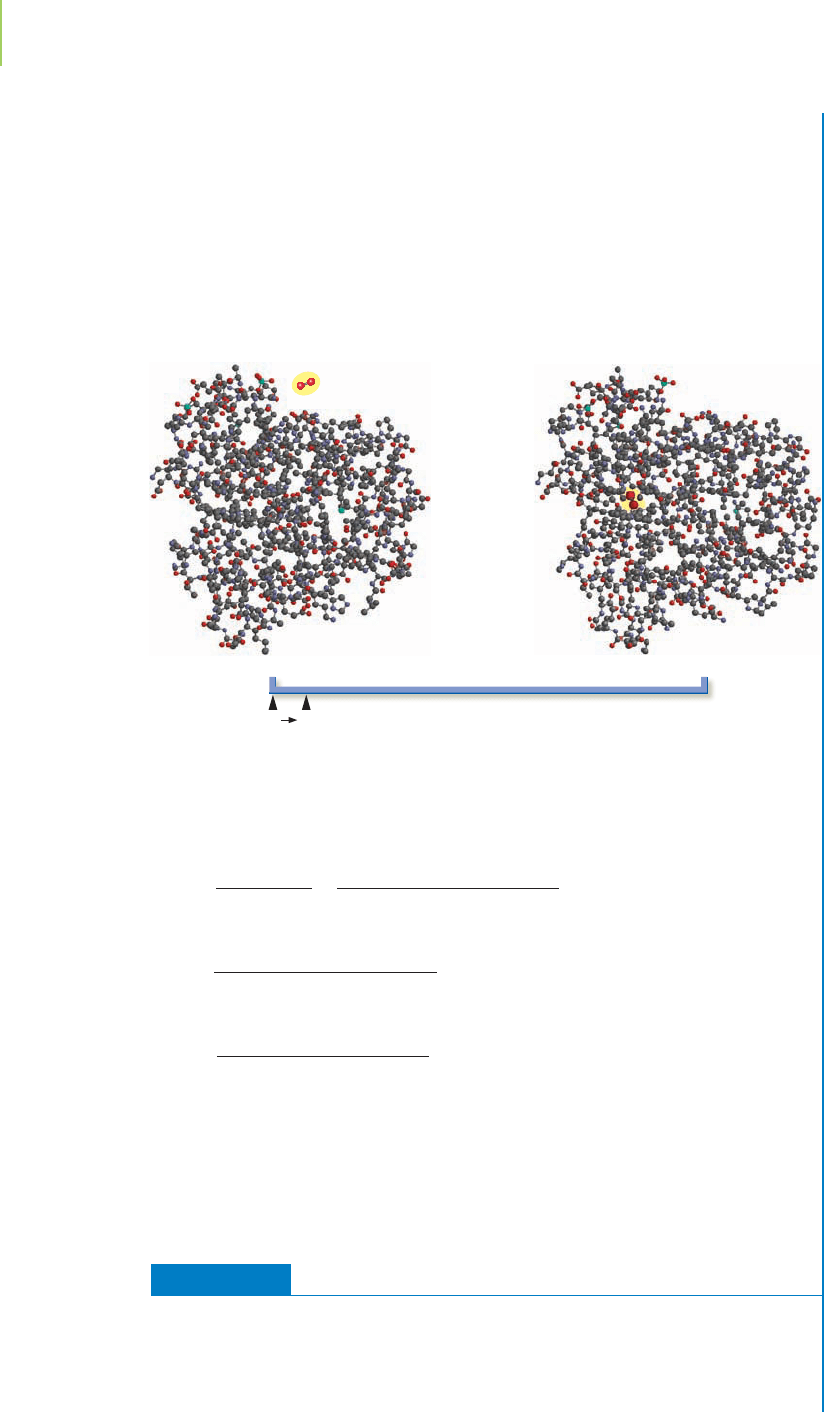
Keep in mind the significance of the reaction quotient, Q. It helps us see in which
direction the reaction will go to reach equilibrium. When the value for K is small, it
is true that the equilibrium position will favor the reactants. However, if you started
off with no products at all, even such a reaction will move (slightly) to the right to
form a little product. We can show this graphically:
Reactants
SE
Products
Reactants
SE
Products
a. Q = 1.5 × 10
5
b. [O
3
] = 1.0 M;[O
2
] = 1.0 M; [NO] = 0.50 M; [NO
2
] = 0.25 M
c. [O
3
] =0.0010 M;[O
2
] =2.55 M; [NO] =1.78 ×10
−6
M; [NO
2
] =5.4 ×10
−3
M
d. [O
3
] = 0.033 M;[O
2
] = 0.019 M; [NO] = 9.3 M; [NO
2
] = 0.044 M
See Problems 45–48.
How can we solve for the amounts of substances
of interest that are present at equilibrium?
The present case study concerns a small value of K. After this, we will look at large
and then intermediate values of K.
Small Value of K
We have a system that contains 0.500 M CH
3
COOH, which ionizes with the rela-
tively small K of 1.8 × 10
−5
. What will be the equilibrium concentrations of
acetate ions (CH
3
COO
−
) and hydrogen ions (H
+
)?
CH
3
COOH(aq)
CH
3
COO
−
(aq) + H
+
(aq) K = 1.8 × 10
−5
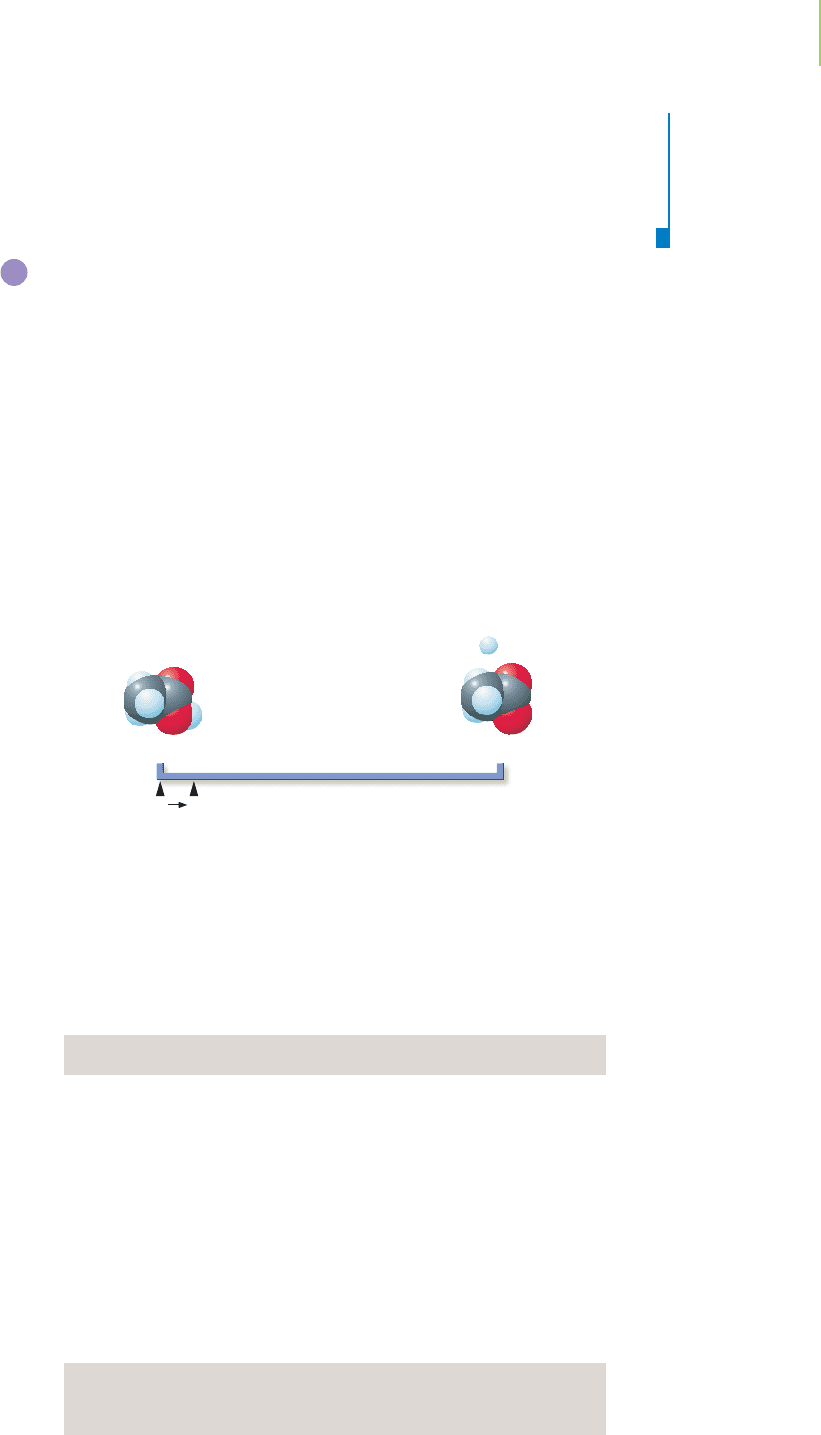
The lack of products initially present, along with the small equilibrium constant,
suggests that the reaction will proceed to the right, but not very far. Our view of
where we start and where we end looks something like this on our equilibrium
line chart:
4
16.5 Solving Equilibrium Problems—A Different Way of Thinking
691
Tracking the changes that take place as we go from the start to equilibrium re-
quires a bit of bookkeeping. Bookkeepers keep track of a company’s finances
using tables that show changes in financial data in an organized, clear way.We will
do the same thing for our equilibrium data by setting up a table that contains the
following rows:
Initial row: The “initial” row includes the initial concentration of each
species.
CH
3
COOH(aq)
CH
3
COO
−
(aq) + H
+
(aq)
initial 0.500 M 0 M 0 M
Change row: The “change” row describes the change in concentration of each
species that occurs in order to reach equilibrium. This must take into account the
stoichiometric ratios among reactants and products in the reaction (all 1-to-1 in
this example) and the magnitude of the equilibrium constant, which in this case
is small enough to indicate that the reaction will not go very far before equilib-
rium is reached. Because we don’t yet know the amount of acetic acid that will
ionize, we call it “x.” The concentration of acetic acid will decrease by “x” M, and
the acetate and hydrogen ion concentrations will increase by “x” M. Again, the
stoichiometry of the equation is included in this line of the table.
CH
3
COOH(aq)
CH
3
COO
−
(aq) + H
+
(aq)
initial 0.500 M 0 M 0 M
change −x +x +x
Equilibrium row: When the free energy change of the reaction equals zero,
such that the free energy itself is at a minimum, the reaction will be at equilib-
rium. The value for each substance in the “equilibrium” row equals the initial
amount plus the change (so that 0.500 +“−x” = 0.500 −x). This is sufficient for
us to proceed with the problem, especially via programmable calculators, which
can solve the necessary equations with a few keystrokes.
CH
3
COOH(aq)
CH
3
COO
−
(aq) + H
+
(aq)
initial 0.500 M 0 M 0 M
change −x +x +x
equilibrium 0.500 − x +x +x
Assumptions row: Whether or not we have a programmable calculator, we
can get a deeper understanding of the equilibria in solution by making key
assumptions. We can simplify the problem solving by assuming that because the
value for K is small, the value of “x” will also be small—that is, there is negligible
ionization compared to our initial acetic acid concentration. We’ll assume that
it will be so small as to be unimportant compared to the initial concentration of
0.500 M. Making that assumption enables us to say that 0.500 −x ≈0.500. How-
ever, because “x” is not unimportant compared to 0 M (any quantity is infinitely
large compared to zero!), we cannot neglect “x” in the other columns of the table.
The “assumptions” row shows the final equilibrium amounts with any assump-
tions we make.
CH
3
COOH(aq)
CH
3
COO
−
(aq) + H
+
(aq)
initial 0.500 M 0 M 0 M
change −x +x +x
equilibrium 0.500 − x +x +x
assumptions 0.500 xx
The table that we have worked with is an expanded version of what is often called
an ICE table, which stands for I
nitial, Change, Equilibrium table. Our expanded
version includes the A
ssumptions row, so we will call this an ICEA table. We will
often use ICEA tables in our equilibrium problem solving because they give us an
organized way to assess the changes in concentration that occur in our reactions.
We can now substitute the equilibrium concentrations generated in the
assumptions row of our table into the mass-action expression and solve for “x.”
K =
[CH
3
COO
−
][H
+
]
[CH
3
COOH]
1.8 × 10
−5
=
(x)(x)
0.500
1.8 × 10
−5
=
x
2
0.500
9.0 × 10
−6
= x
2
3.0 × 10
−3
= x
Now, if we return the value of “x”to our ICEA table and solve for the assumptions
row, we obtain the equilibrium concentrations of all species in the reaction,
assuming our assumption is justified.
692 Chapter 16 Chemical Equilibrium
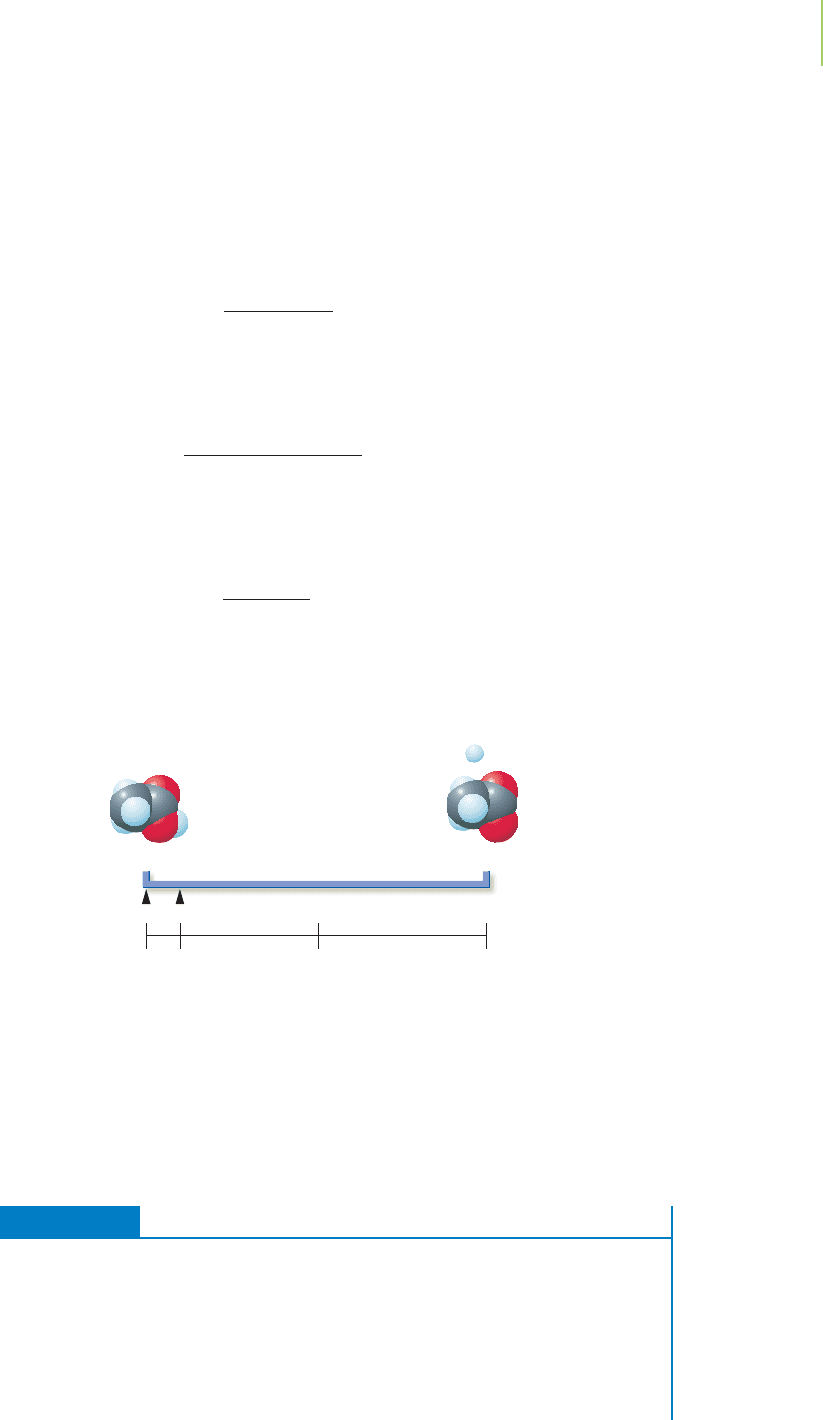
Reactants
0% 0.6% 50%
Extent of reaction
100%
SE
Products
x = [CH
3
COO
−
] = [H
+
] = 3.0 × 10
−3
M
Theactualequilibriumconcentrationof acetic acidis0.500−3.0 ×10
−3
=0.497 M,
or 0.50 M to two significant figures.
Do our results make sense? That is, are they
reasonable?
We can determine that our results are mathematically correct by sub-
stituting the concentration values back into the equilibrium expression to show
that this results in K.
(3.0 ×10
−3
)
2
0.50
= 1.8 × 10
−5
Was our assumption justified? In other words, was “x” negligible compared to the
original acetic acid concentration? We say that our assumption is valid if the
change as a result of the assumption is less than 5% of the original concentration.
x
original concentration
× 100% ≤ 5%
Although we will use this “5% rule” in our work, professional chemists some-
times require a smaller tolerance, and sometimes a larger, depending on the
process with which they are working. With our data,
3.0 ×10
−3
0.500
× 100%
= 0.6%
and using the 5% rule, we find that our assumption of negligible ionization
(0.6%, in this case) was valid.
Let’s revisit our equilibrium line chart and see what 0.6% ionization means in
terms of the extent of the reaction.
This confirms our initial thinking that with the very small value for K, the
reaction would not proceed—acetic acid would not ionize—appreciably.
To be sure our calculations are valid, we should also test our other assump-
tion, that the ionization of water is unimportant. This is a more complex issue
that we will consider in Chapter 17.
H
2
O
H
+
+ OH
−
K = 1.0 × 10
−14
EXERCISE 16.8 Concentration of Lead Ion in Saturated Lead Bromide
Determine the concentration of lead ion in a saturated solution that would result
from the dissolution of solid lead(II) bromide, PbBr
2
(s).
PbBr
2
(s)
Pb
2+
(aq) + 2Br
−
(aq) K = 4.6 × 10
−6
at 25°C
First Thoughts
What is the important chemistry that occurs in solution? The only important chem-
istry of interest is the dissolution of the lead bromide, which is a largely insoluble
16.5 Solving Equilibrium Problems—A Different Way of Thinking 693

Our equilibrium line chart is similar to that for the dissociation of acetic acid. What
are the equilibrium concentrations of substances? We can use the same style of table
as we did with the acetic acid dissociation. Our only modification arises because
lead bromide is a pure solid, so it is not part of the equilibrium expression. We show
this in the ICEA table below.
PbBr
2
(s)
Pb
2+
(aq) + 2Br
−
(aq)
initial — 0 M 0 M
change — +x +2x
equilibrium — x 2x
The concentration of the solid reactant is constant. In this table, “x” represents the
amount of PbBr
2
(s) that dissolves. This value is therefore equal to the solubility of
the salt. Because the initial amount of each product was 0 M, the amount gained,“x”
and “2x,” is not negligible compared to 0 M; therefore, we made no assumptions.
Note that we use “2x” to represent the change in [Br
−
] because bromide has a stoi-
chiometric factor of 2 in the equation. This stoichiometric factor will also come in
to play when we write the mass-action expression.
Solution
How can we solve for the amounts of substances of interest that are present at equi-
librium? We can substitute our concentrations into the mass-action expression for
the equation:
K = [Pb
2+
][Br
−
]
2
4.6 × 10
−6
= (x)(2x)
2
4.6 × 10
−6
= 4x
3
[Pb
2+
] = x = 1.048 × 10
−2
M ≈ 1.0 × 10
−2
M
[Br
−
] = 2x = 2.096 × 10
−2
M ≈ 2.1 × 10
−2
M
We check our answer by solving for K.
K = (1.048 × 10
−2
) × (2.096 × 10
−2
)
2
= 4.6 × 10
−6
This agrees well with the actual value of K.
Further Insights
Do our results make sense? The concentrations for the ions that we calculated are
quite low, and that makes sense, given the very low value for K.
694 Chapter 16 Chemical Equilibrium
Reactants
SE
Products
salt, judging by the small value of K. In which direction will the reaction proceed?
Even though the equilibrium constant is quite small, the reaction will proceed
(minimally) to the products side because there were no products present initially.
PRACTICE 16.8
What is the concentration of lead ion in a saturated solution of PbCl
2
?
PbCl
2
(s)
Pb
2+
(aq) + 2Cl
−
(aq) K = 1.6 × 10
−5
at 25°C
See Problems 49, 50, 55, 56, and 60.
In Exercise 16.8, only one important equilibrium needed to be considered.As our
understanding of equilibrium deepens, we will find that more than one reaction
may well be important. For example, although it wasn’t illustrated, the chemical
interaction of Pb
2+
and Br
−
with water were considered. In both of these cases,
the interaction is minimal, so the dissolution of PbBr
2
was the only equilibrium
of importance. However, if instead of PbBr
2
we had attempted to calculate the
concentration of lead ion from the dissolution of PbS, the reaction of S
2−
with
water would have been very important, as illustrated by the equilibria below. In
this case, both equations would need to be considered.
PbS(s)
Pb
2+
(aq) + S
2−
(aq) K = 7 × 10
−29
S
2−
(aq) + H
2
O(l)
HS
−
+ OH
−
K = 0.083
Including the formation of HS
−
in our calculations would modify the solubility
of lead(II) sulfide. We will learn how to deal quantitatively with multiple equilib-
ria in Chapter 18.
Large Value of K
The reaction of sulfur dioxide and oxygen to form sulfur trioxide at 400°C serves
as an excellent model with which to examine systems that have large equilibrium
constants, in which the reaction is essentially complete.
2SO
2
(g) + O
2
(g)
2SO
3
(g) K = 8.7 × 10
6
If the initial concentrations of SO
2
and O
2
are 1.0 × 10
−3
M and
2.0 ×10
−3
M, respectively, what is the equilibrium concentration of
SO
3
? Given the large equilibrium constant, we can assume that the
reaction goes to completion, except for a small amount, “2x,” that
remains unreacted. Remember that the “2x” indicates the stoichiom-
etry of the reaction. An equilibrium line chart can help us visualize
the extent of reaction.
This is, in effect, a limiting reactant problem in which SO
2
is the
limiting reactant. On the basis of the reaction stoichiometry and the
large value of K, we can develop an ICEA table. We complete the first
row of the table by writing the initial concentration of each species
in the reaction.
2SO
2
(g) + O
2
(g)
2SO
3
(g)
initial 1.0 × 10
−3
M 2.0 × 10
−3
M 0 M
The “change” row in our ICEA table will be a little different than before. We
have said that the equilibrium constant is large, and this means the reaction will
go essentially to completion. However, we must hold a tiny amount of each reac-
tant back because the reaction will not go all the way to products. Let’s indicate the
small amount that remains behind as “2x” for SO
2
and “x”for O
2
. That is the
“+2x” and “+x” that we place in the respective concentrations in the change row.
Other than those small amounts that remain, all of the SO
2
that can react will do so.
That means, based on the reaction stoichiometry, that 1.0 × 10
−3
M SO
2
and
0.5 × 10
−3
M O
2
will react (less the “2x” and “x” amounts of reactants that
16.5 Solving Equilibrium Problems—A Different Way of Thinking 695
Reactants
SE
Products

remain) to form 1.0 × 10
−3
M SO
3
(less the “2x” that is unreacted). The total
[SO
2
] that will react, then, is all of it except for the 2x that remains. This is where
we get the change of −1.0 × 10
−3
+ 2x. In other words, all of it forms products
except for the small amount,“2x,” that does not react and remains. Because of the
2-to-1 mole ratio of SO
2
to O
2
, 0.5 ×10
−3
M O
2
will react with 1.0 ×10
−3
M SO
2
.
And if 2x mol of SO
2
remains unreacted, x mol of O
2
will be unreacted. This is
why the change in concentration of O
2
is −0.5 × 10
−3
+ x.
2SO
2
(g) + O
2
(g)
2SO
3
(g)
initial 1.0 × 10
−3
M 2.0 × 10
−3
M 0 M
change −1.0 × 10
−3
+ 2x −0.5 × 10
−3
+ x 1.0 × 10
−3
−2x
The equilibrium row is, again, the result of adding together the initial and change
entries in each column.
2SO
2
(g) + O
2
(g)
2SO
3
(g)
initial 1.0 × 10
−3
M 2.0 × 10
−3
M 0 M
change −1.0 × 10
−3
+ 2x −0.5 × 10
−3
+ x 1.0 × 10
−3
− 2x
equilibrium 2x 1.5 ×10
−3
+ x 1.0 × 10
−3
− 2x
In the last row of the table, the “assumptions” row, we make the assumption that
“x” is small. If this is true, then 1.5 × 10
−3
+ x ≈ 1.5 × 10
−3
. And, if that is true,
then 1.0 × 10
−3
− 2x ≈ 1.0 × 10
−3
must be true as well.
2SO
2
(g) + O
2
(g)
2SO
3
(g)
initial 1.0 × 10
−3
M 2.0 × 10
−3
M 0 M
change −1.0 × 10
−3
+ 2x −0.5 × 10
−3
+ x 1.0 × 10
−3
− 2x
equilibrium 2x 1.5 ×10
−3
+ x 1.0 × 10
−3
− 2x
assumptions 2x 1.5 × 10
−3
1.0 × 10
−3
We then write the mass-action expression, plug our assumptions row values into
the equation, and solve for “x”:
K =
[SO
3
]
2
[SO
2
]
2
[O
2
]
=
(1.0 ×10
−3
)
2
(2x)
2
(1.5 ×10
−3
)
= 8.7 ×10
6
4x
2
= 7.66 × 10
−11
x = 4.38 × 10
−6
M
2x = [SO
2
] = 8.75 × 10
−6
≈ 8.8 ×10
−6
M
Does this answer make sense? Substituting back into the mass-action expression
shows that our equation is mathematically valid.
(1.0 ×10
−3
)
2
(8.75 ×10
−6
)
2
(1.5 ×10
−3
)
= 8.7 ×10
6
M
Is our assumption valid? That is, is the value of “x” negligible compared to
1.5 ×10
−3
M?
x
original concentration
× 100% =
4.38 ×10
−6
M
1.5 ×10
−3
M
× 100% = 0.29%
696 Chapter 16 Chemical Equilibrium
This easily passes the 5% test, so our assumption that “x” is negligible compared
to the initial concentrations of O
2
and SO
3
is valid.
EXERCISE 16.9 The Myoglobin–Oxygen System
Solve for the equilibrium concentrations of myoglobin, oxygen, and the MbO
2
complex, given the following initial concentrations. Assume that the myoglobin-
oxygen reaction is the most important reaction in this system. In other words,
you may neglect the ionization of water because its equilibrium constant is rela-
tively very small.
[Mb]
0
= 2.0 × 10
−4
M;[O
2
]
0
= 1.9 × 10
−5
M; [MbO
2
]
0
= 0 M
Mb + O
2
MbO
2
K = 8.6 × 10
5
First Thoughts
The value of the equilibrium constant, K, is large, so the reaction will be nearly com-
plete at equilibrium. We have a 1-to-1 mole ratio of myoglobin to oxygen, but we
don’t have enough oxygen ([O
2
]
0
=1.9 ×10
−5
M ) to react with all of the myoglobin
([Mb]
0
= 2.0 × 10
−4
M). Therefore, this is a limiting reactant problem, with oxygen
as the limiting reactant—there is excess myoglobin.
Solution
We set up the ICEA table, write the mass-action expression, and solve for “x.” Our
assumption, that “x” is small compared to 1.9 × 10
−5
, will need to be checked.
Mb + O
2
MbO
2
initial 2.0 × 10
−4
M 1.9 × 10
−5
M 0 M
change −1.9 × 10
−5
+ x −1.9 × 10
−5
+ x 1.9 × 10
−5
− x
equilibrium 1.81 × 10
−4
+ xx1.9 × 10
−5
− x
assumptions 1.81 × 10
−4
x 1.9 × 10
−5
K =
[MbO
2
]
[Mb][O
2
]
=
(1.9 ×10
−5
)
(1.81 ×10
−4
)(x)
= 8.6 ×10
5
x = [O
2
] = 1.22 × 10
−7
M ≈1.2 × 10
−7
M
[Mb] = 1.81 × 10
−4
+ x ≈ 1.8 × 10
−4
M
[MbO
2
] = 1.9 × 10
−5
− x ≈ 1.9 × 10
−5
M
The value of “x” is well under 5% of our initial concentrations, so our assumption
that “x” is negligible is valid. Checking our math yields
(1.9 ×10
−5
)
(1.81 ×10
−4
)(1.22 ×10
−7
)
= 8.6 ×10
5
= K
Further Insights
A famous advertising campaign used to talk about pork as “the other white meat,”
the conventional white meat being chicken. Beef is redder than chicken or pork be-
cause of its myoglobin content in the muscles, which averages (give or take quite a
bit) about 8 mg of myoglobin per gram of meat. Pork averages only about 2 mg of
myoglobin per gram of meat, and chicken has about 1 to 3 mg of myoglobin per
gram of meat. Dogs average about 7 mg/g, rats about 2 mg/g, and whales, who
16.5 Solving Equilibrium Problems—A Different Way of Thinking 697
