Карпова И.П. Исследование и разработка подсистемы контроля знаний в распределенных автоматизированных обучающих системах

Подождите немного. Документ загружается.

131

Сравнение двухуровневых схем показало, что с точки зрения

вероятности случайного ввода правильного ответа схема СПИСОК

МНОЖЕСТВ значительно лучше схемы МНОЖЕСТВО СПИСКОВ.

3.5. Моделирование случайного ввода правильного ответа

Разработанные методы оценки ответов типа СПИСОК и МНОЖЕСТВО

позволяют определять правильность ответов не по двухбалльной шкале

(0, 1), а на интервале [0,1]. При использовании этих методов вероятность

случайного ввода абсолютно правильного ответа соответствует формулам

(3.16, 3.18, 3.21–3.22), но появляются "частично правильные ответы", оценка

которых отлична от нуля. Распределение вероятностей появления всех

возможных оценок в интервале [0,1] можно определить по формуле:

)φ(a

∑

где M – общее количество ответов, φ(a

) – функция определения оценки

ответа a

. Оценка ответа зависит от самого ответа (от его сходства с

эталоном), и посчитать по этой формуле распределение вероятностей нельзя.

Поэтому было проведено программное моделирование различных схем

построения ответа для множеств вариантов разных мощностей.

Моделирование проводилось при следующих условиях:

1) Если S

= {a

} – ответ, а S

= {e

} – эталон, то {a

}⊂{e

2) ∀a

: a

∈S

, a

∈S

, i ≠ j ⇒ a

≠ a

3.5.1. Моделирование ответа типа МНОЖЕСТВО

Моделирование ответа типа МНОЖЕСТВО проводилось для N = 3÷7 и

схем "N вариантов ответа – из них 1 правильный" и "N вариантов ответа – из

них k правильных".

Результаты моделирования ответа типа МНОЖЕСТВО представлены на

рис. 3.7–3.10.

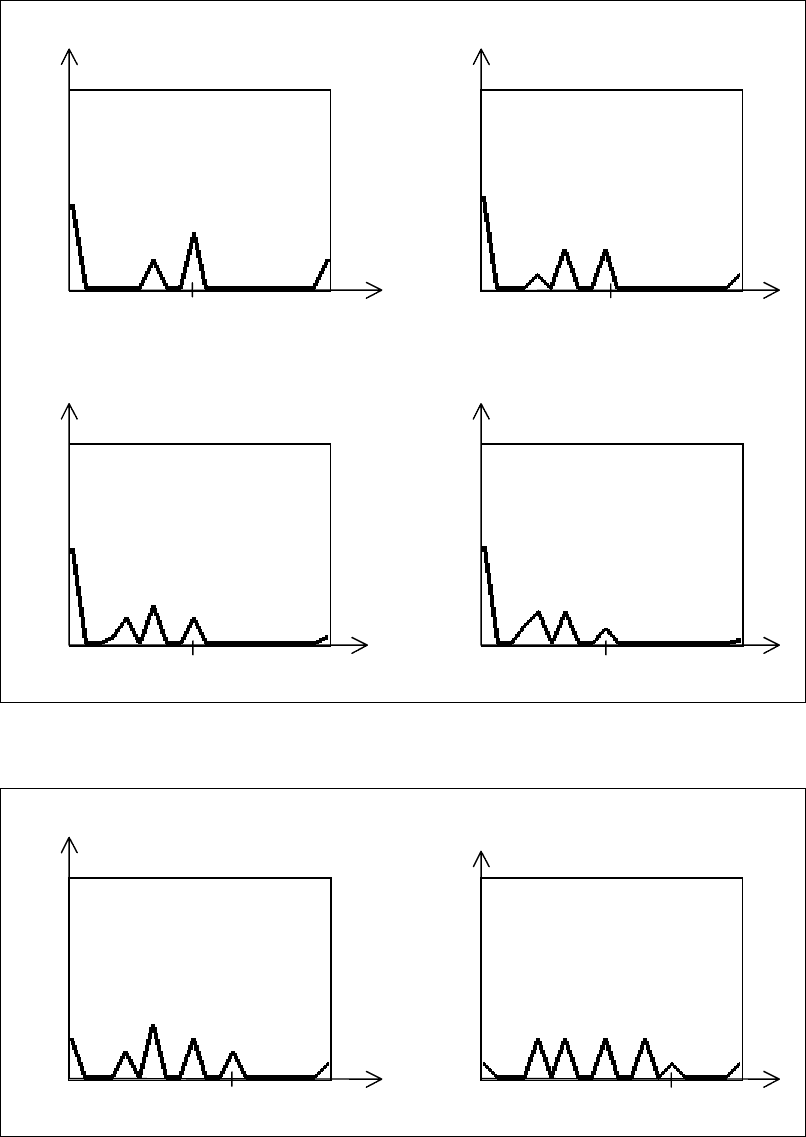
132

Примечание: на рисунках, отражающих результаты моделирования, для каждого

графика указана погрешность (число на оси δ, выделенное курсивом), при

использовании которой высший балл (единица по двухбалльной шкале)

будет поставлен только за правильный ответ.

0.5

1 0

0.5

а) 1 правильный из 3 вариантов б) 1 правильный из 4 вариантов

0.5

1 0

0.5

в) 1 правильный из 5 вариантов г) 1 правильный из 6 вариантов

δδ

Рис. 3.7. Распределение оценок для ответов типа МНОЖЕСТВО,

схема "N вариантов ответа – из них 1 правильный"

0.67

1 0

0.75

а) 2 правильных из 4 вариантов б) 3 правильных из 4 вариантов

Рис. 3.8. Распределение оценок для ответов типа МНОЖЕСТВО,

схема "N вариантов ответа – из них k правильных" (N=4)

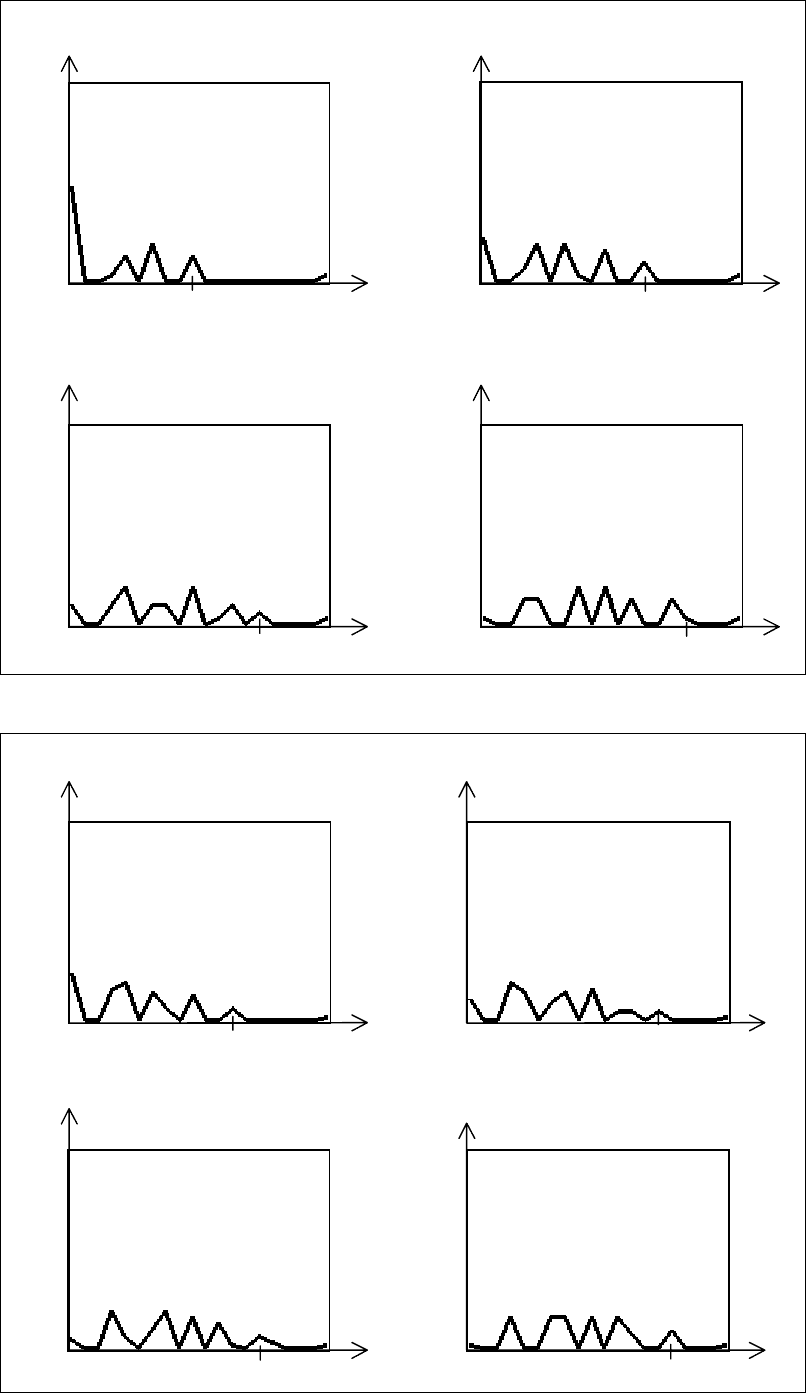
133

0.5

0.6

а) 1 правильный из 5 вариантов б) 2 правильных из 5 вариантов

0.75

1 0

0.8

в) 3 правильных из 5 вариантов г) 4 правильных из 5 вариантов

Рис. 3.9. Распределение оценок для ответов типа МНОЖЕСТВО (N=5)

0.6

1 0

0.75

а) 2 правильных из 6 вариантов б) 3 правильных из 6 вариантов

0.8

1 0

0.8

в) 4 правильных из 6 вариантов г) 5 правильных из 6 вариантов

δδ

Рис. 3.10. Распределение оценок для ответов типа МНОЖЕСТВО (N=6)

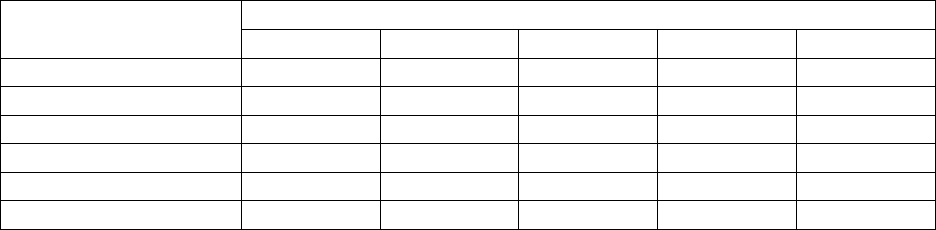
134

Математическое ожидание MX для вероятности случайного ввода

правильного ответа равно:

∑

pδMX

Значения математического ожидания вероятности случайного ввода

правильного ответа для ответа типа МНОЖЕСТВО приведены в табл. 3.4.

Таблица 3.4. Математическое ожидание для ответа типа МНОЖЕСТВО

Количество вариантов ответов Количество

правильных ответов

3 4 5 6 7

1 0.33

0.25 0.20 0.17 0.14

2 0.48 0.38

0.32 0.27 0.24

3 — 0.47 0.40 0.35

0.32

4 — — 0.46 0.41 0.38

5 — — — 0.46 0.43

6 — — — — 0.47

Анализируя графики распределения оценок ответов типа

МНОЖЕСТВО (рис. 3.7–3.10) и табл. 3.4 можно дать следующие

рекомендация для применения таких ответов в тестах:

1. При использовании стандартной шкалы оценок (2, 3, 4, 5) и схемы "N

вариантов ответа – из них 1 правильный" количество вариантов ответов

должно быть не менее четырех (для N=3 математическое ожидание равно

0.36, что при приведении к стандартной шкале дает 3.1 балла, т.е. оценку

"удовлетворительно").

2. Увеличение количества правильных вариантов ответа ведет к увеличению

вероятности случайного получения более высокой оценки. Поэтому не

следует использовать дифференцированную оценку ответа в тех случаях,

когда необходим точный ответ и наличие "лишних" вариантов (или

отсутствие требуемых) должно расцениваться как неверный ответ.

3.5.2. Моделирование ответа типа СПИСОК

Моделирование ответа типа СПИСОК проводилось для N = 4÷7 и схем

"N вариантов ответа – есть лишние" и "N вариантов ответа – нет лишних".

Результаты приведены на рис. 3.11–3.13, значения математического

ожидания вероятности случайного ввода правильного ответа – в табл. 3.5.

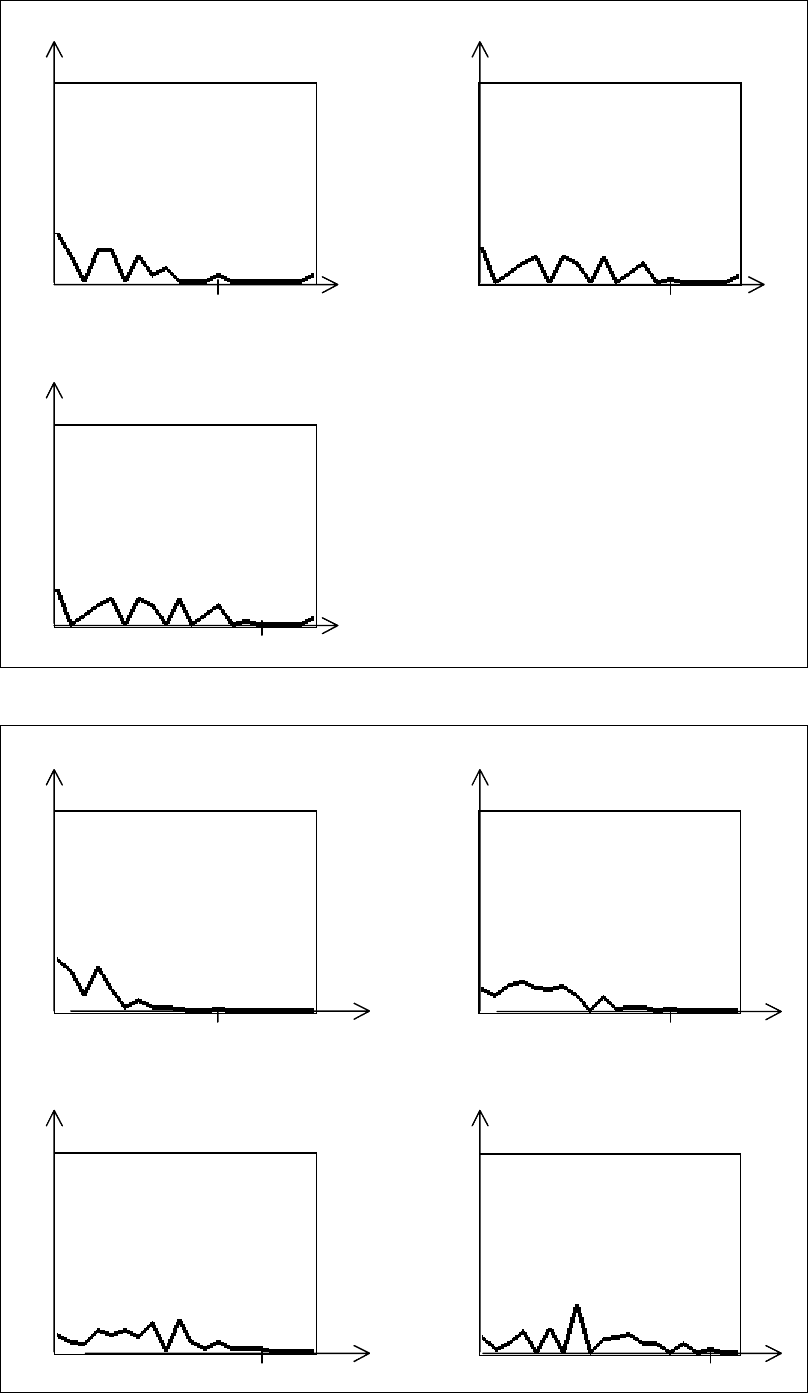
135

а) 4 варианта, список длиной 2 б) 4 варианта, список длиной 3

0.65

1 0

0.75

0.8

в) 4 варианта, список длиной 4

Рис. 3.11. Распределение оценок для ответов типа СПИСОК (N=4)

а) 5 вариантов, список длиной 2 б) 5 вариантов, список длиной 3

0.65

1 0

0.75

1 1

0.8

1 0

0.9

в) 5 вариантов, список длиной 4 г) 5 вариантов, список длиной 5

Рис. 3.12. Распределение оценок для ответов типа СПИСОК (N=5)

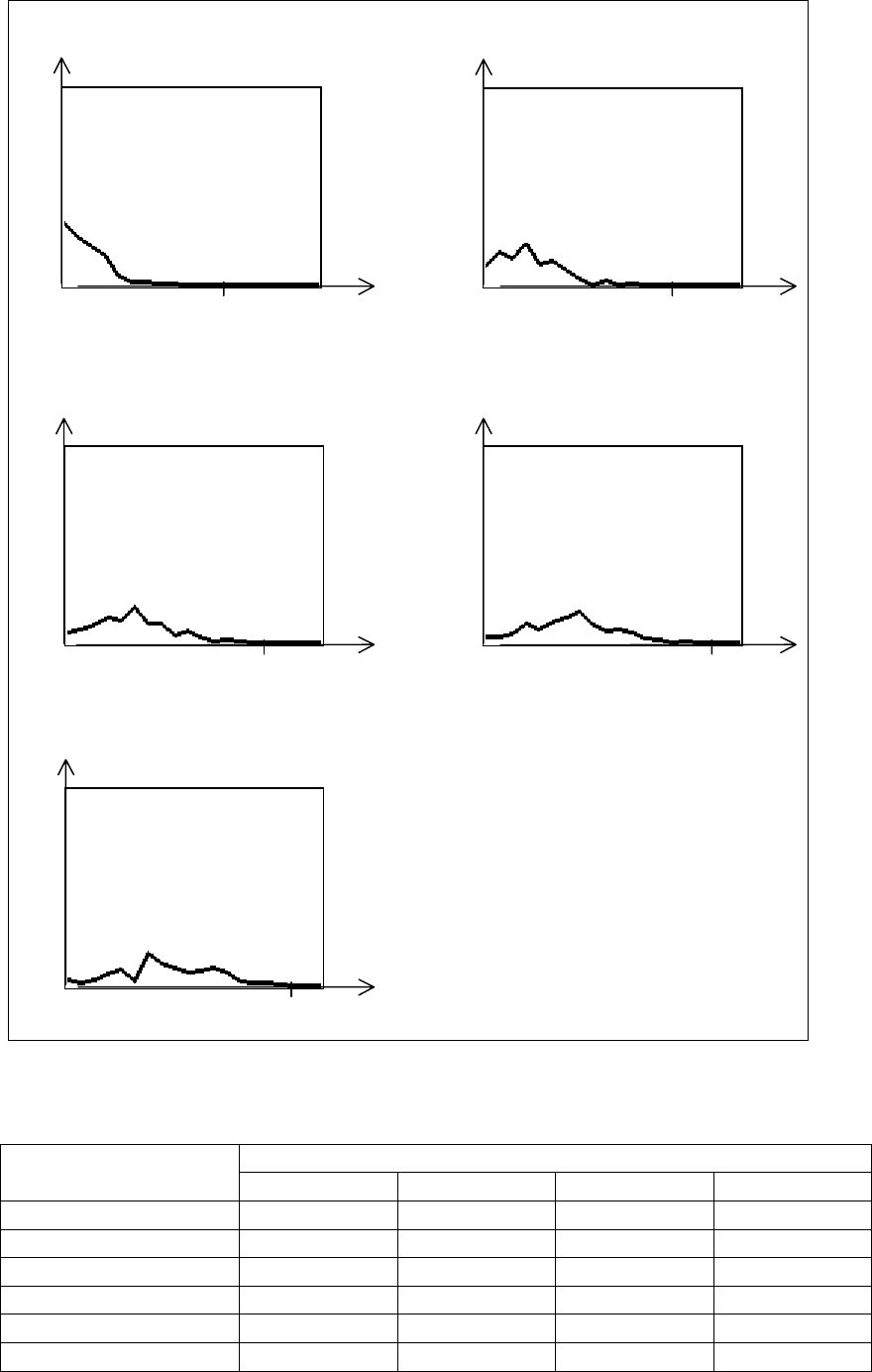
136

а) 6 вариантов, список длиной 2 б) 6 вариантов, список длиной 3

0.65

1 0

0.75

1 1

0.8

0.9

в) 6 вариантов, список длиной 4 г) 6 вариантов, список длиной 5

0.9

в) 6 вариантов, список длиной 6

δδ

Рис. 3.13. Распределение оценок для ответов типа СПИСОК (N=6)

Таблица 3.5. Математическое ожидание для ответа типа СПИСОК

Количество вариантов ответов Количество ответов,

входящих в список

4 5 6 7

0.27 0.16 0.11 0.08

3 0.35

0.26 0.19 0.15

4 0.42 0.35

0.28 0.23

5 — 0.41 0.35

0.29

6 — — 0.42 0.37

7 — — — 0.43

137

Анализ графиков распределения оценок ответов типа СПИСОК

(рис. 3.11–3.13) и табл. 3.5 показывает: для того, чтобы исключить

возможность случайно получить удовлетворительную оценку при

использовании стандартной шкалы оценок (2, 3, 4, 5), нужно предлагать для

вопроса не менее двух "лишних" вариантов.

3.5.3. Моделирование ответа типа СПИСОК МНОЖЕСТВ

Для сравнения списков множеств в п. 3.3.3.4. "Списки множеств"

предлагались два очевидных алгоритма сравнения списков множеств:

(А1) – множества, входящие в ответ, считаются упорядоченными, поэтому i-

й элемент ответа сравнивается с i-м элементом эталона (более короткий

список дополняется пустыми множествами).

(А2) – ответ не считается упорядоченным, поэтому каждый элемент ответа

сравнивается с каждым элементом эталона. Элементы ответа a

эталона e

сопоставляются в соответствии с максимальной суммой

степеней сходства δ элементов ответа и эталона, и оценивается

упорядочивание элементов a

на основе меры порядка, введенной

эталоном {e

} (т.е. оценка происходит два этапа).

Второй алгоритм дает более точную оценку. Но первый алгоритм работает

значительно быстрее за счет исключения определения максимальной суммы,

которое является NP-полной задачей с временной сложностью N!.

Сравним результаты моделирования этими алгоритмами для того,

чтобы определить возможность использования алгоритма (А1) для ускорения

анализа ответа без существенной потери качества. Результаты приведены в

табл.3.6 (математическое ожидание случайного ввода правильного ответа) и

табл.3.7 (корреляция между оценками ответов, рассчитанная как среднее

квадратичное отклонение).

Как видно из результатов, погрешность оценок достаточно высока

(10% и более), поэтому для моделирования ответов типа СПИСОК

МНОЖЕСТВ использовался алгоритм (А2).

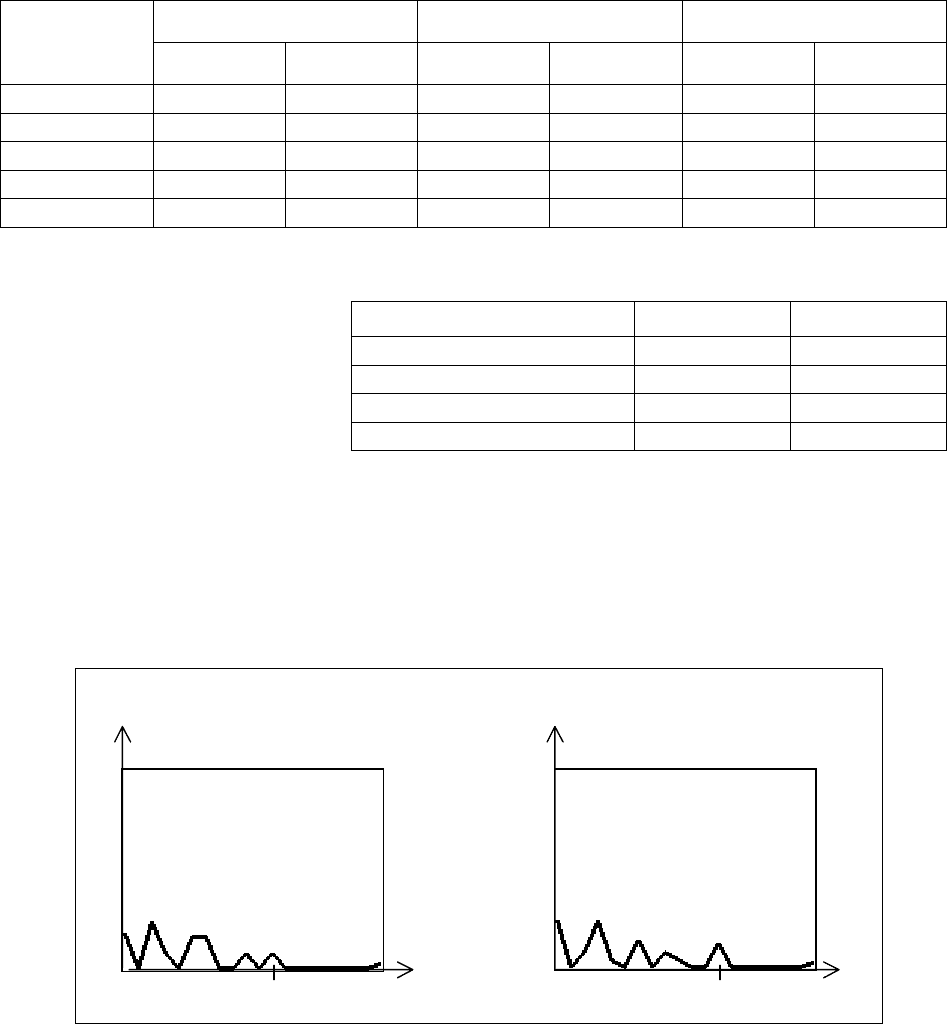
138

Таблица 3.6. Математическое ожидание случайного ввода правильного ответа

для СПИСКА МНОЖЕСТВ при использовании алгоритмов (А1) и (А2)

5 вариантов 6 вариантов 7 вариантов

Количество

множеств, N

(А1) (А2) (А1) (А2) (А1) (А2)

2 0.16 0.19 0.11 0.15 0.078 0.119

3 0.19 0.27 0.15 0.23 0.107 0.188

4 0.20 0.33 0.16 0.30 0.123 0.267

5 – – 0.17 0.34 0.138 0.295

6 – – – – 0.143 0.330

Таблица 3.7. Корреляция между оценками

при использовании алгоритмов (А1) и (А2)

Количество множеств, N 5 вариантов 6 вариантов

2 0.12 0.10

3 0.19 0.15

4 0.23 0.21

5 – 0.25

Моделирование проводилось для N = 4÷7 и схемы "N вариантов ответа

– нет лишних". Результаты приведены на рис. 3.14–3.17, значения

математического ожидания вероятности случайного ввода правильного

ответа – в табл. 3.8.

а) 4 варианта, 2 множества б) 4 варианта, 3 множества

0.6

1 0

0.65

Рис. 3.14. Распределение оценок для ответов типа СПИСОК МНОЖЕСТВ (N=4)

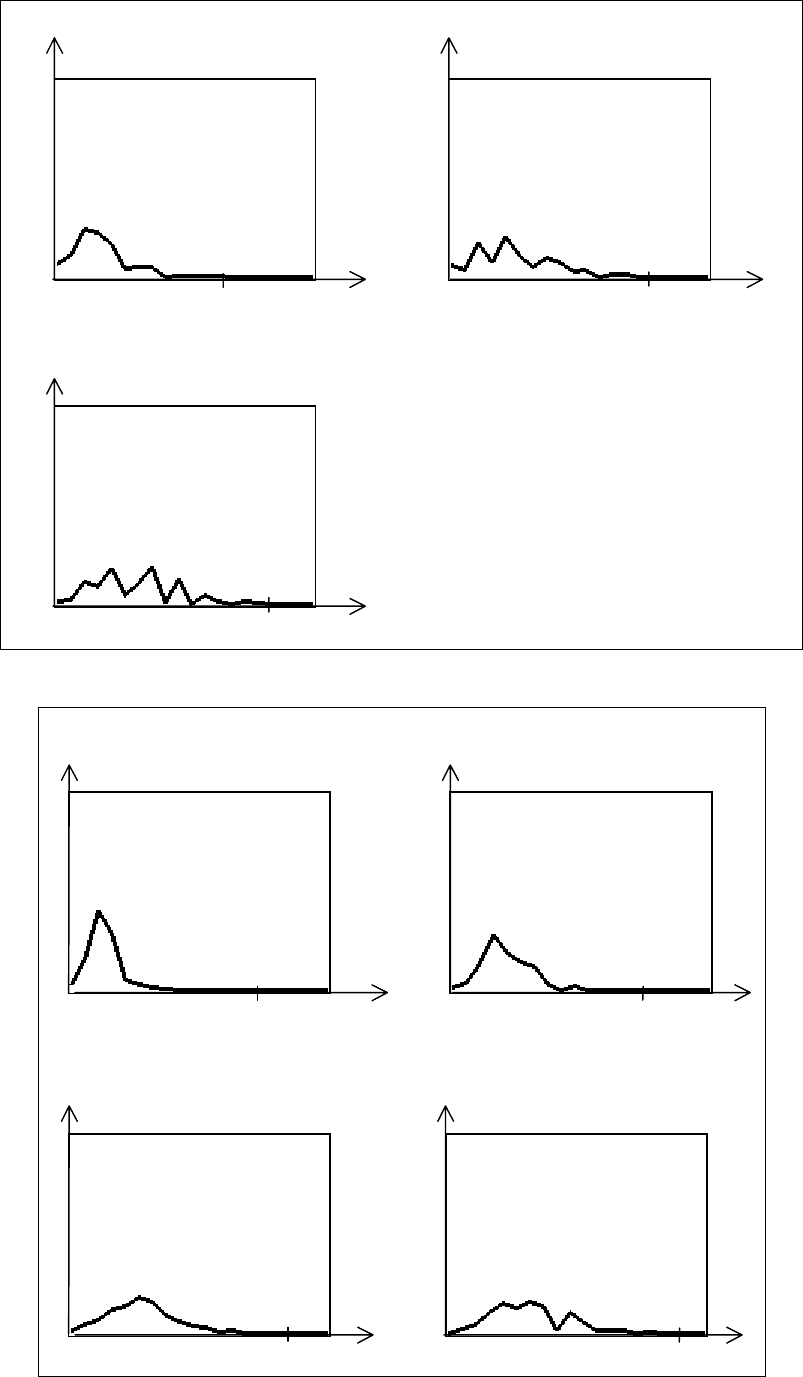
139

0.7

1 0

0.75

а) 5 вариантов, 2 множества б) 5 вариантов, 3 множества

в) 5 вариантов, 4 множества

0.8

Рис. 3.15. Распределение оценок для СПИСКА МНОЖЕСТВ (N=5)

а) 6 вариантов, 2 множества б) 6 вариантов, 3 множества

0.7

1 0

0.7

в) 6 вариантов, 4 множества г) 6 вариантов, 5 множеств

0.8

1 0

0.9

δδ

Рис. 3.16. Распределение оценок для СПИСКА МНОЖЕСТВ (N=6)

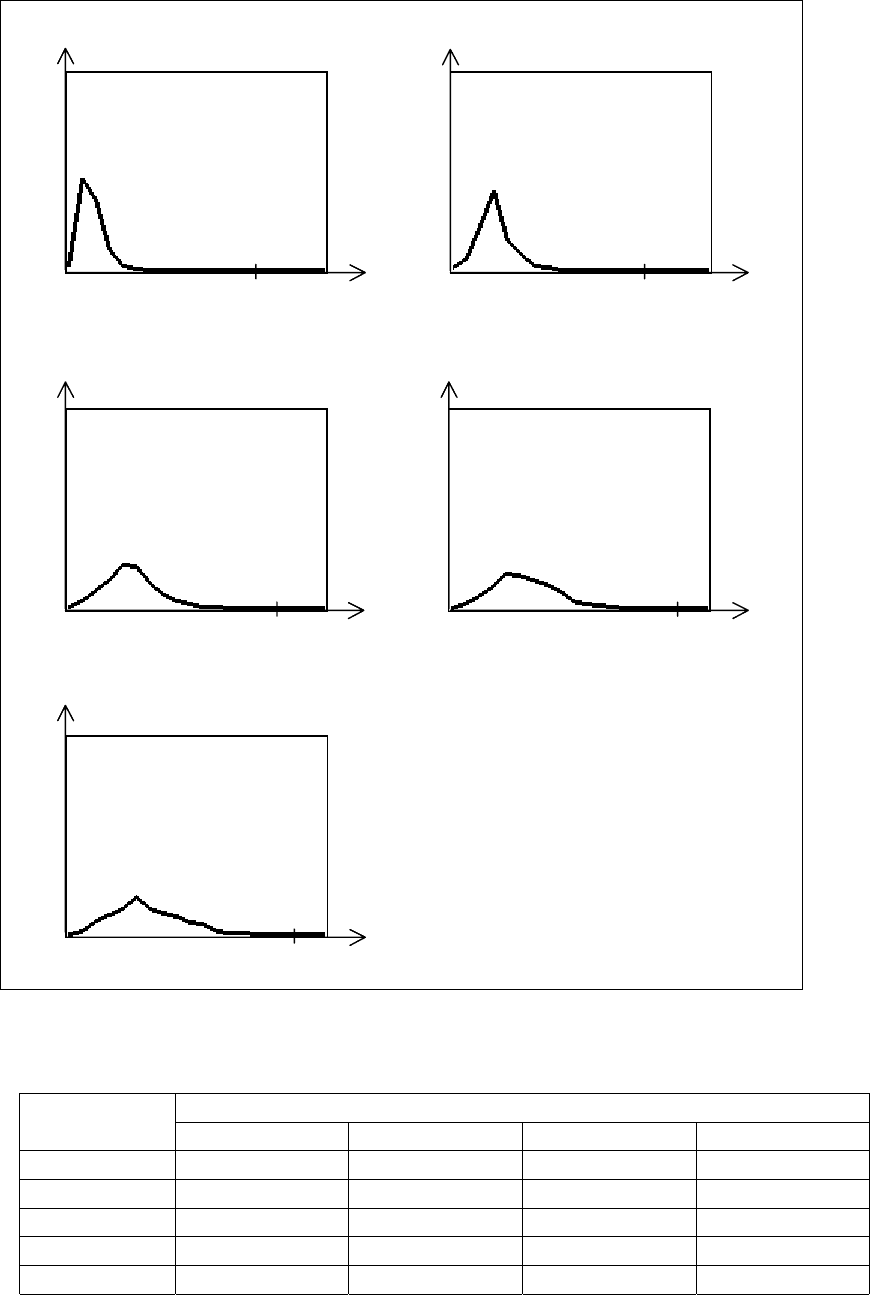
140

0.75

1 0

0.75

а) 7 вариантов, 2 множества б) 7 вариантов, 3 множества

в) 7 вариантов, 4 множества г) 7 вариантов, 5 множеств

0.8

1 0

0.9

д) 7 вариантов, 6 множеств

0.9

δδ

Рис. 3.17. Распределение оценок для СПИСКА МНОЖЕСТВ (N=7)

Таблица 3.8. Математическое ожидание для ответа типа СПИСОК МНОЖЕСТВ

Количество вариантов ответов Количество

множеств

4 5 6 7

0.26 0.19 0.15 0.12

0.31 0.27 0.23 0.19

4 — 0.33

0.30 0.27

5 — — 0.34

0.30

6 — — — 0.33

Анализ результатов моделирования для схемы СПИСОК МНОЖЕСТВ

показывает, что эта схема имеет хорошие характеристики и может

применяться даже при N=5.