Капра Фритьоф. Паутина жизни. Новое научное понимание живых систем

Подождите немного. Документ загружается.

Рис. 6-10. Аттрактор Уэда. Из Ueda et al. (1993)

Аттрактор Уэда — это траектория в двухмерном фазовом пространстве,

которая образует почти повторяющие друг друга паттерны. Это типичная

особенность хаотических систем. Изображение на рис. 6-10 содержит

более 1 000 000 точек. Ее можно представить в виде среза куска теста,

который многократно растягивали и сворачивали. Это означает, что в

основе аттрактора Уэда лежит математика преобразования пекаря.

Одно удивительное свойство странных аттракторов заключается в том,

что они, как правило, ограничены малым числом измерений — даже в

многомерном фазовом пространстве. Например, система может содержать

50 переменных, но ее движение при этом описывается трехмерным

странным аттрактором — свернутой поверхностью в 50-мерном

пространстве. Это, естественно, характеризует высокую степень порядка.

Таким образом, хаотичное поведение — в современном научном

понимании этого термина — разительно отличается от беспорядочного,

неустойчивого движения. С помощью странных аттракторов можно

определить различие между обычной беспорядочностью, или шумом, и

хаосом. Хаотичное поведение детерминировано и образует паттерны, а

странные аттракторы позволяют преобразовывать на первый взгляд

случайные данные в отчетливые визуальные формы.

«Эффект бабочки»

Как мы видели на примере преобразования пекаря, для хаотических

систем характерна чрезвычайная чувствительность к начальным условиям.

Мельчайшие изменения в начальном состоянии системы со временем

приводят к крупномасштабным последствиям. В теории хаоса это

называется «эффектом бабочки». Основой для названия послужило

полушутливое утверждение, что бабочка, всколыхнув сегодня воздух в

Пекине, может через месяц оказаться причиной бури в Нью-Йорке.

Эффект бабочки был открыт в начале 1960-х годов метеорологом

Эдвардом Лоренцом, разработавшим очень простую модель погодных

условий, состоящую из трех связанных нелинейных уравнений. Он

обнаружил, что решения его уравнений чрезвычайно чувствительны к

начальным состояниям. Начинаясь практически в одной точке, две

траектории будут развиваться совершенно по-разному, исключая

возможность каких бы то ни было заблаговременных предсказаний

Это открытие привело в замешательство все мировое научное

сообщество, поскольку ученые давно привыкли полагаться на

детерминированные уравнения для предсказания с большой точностью

таких феноменов, как солнечные затмения или появление комет. Казалось

непостижимым, что четко детерминированные уравнения движения могут

привести к непредсказуемым результатам. И все же именно это обнаружил

Лоренц. По его собственным словам:

Обычный человек, видя, что мы достаточно эффективно

предсказываем приливы на несколько месяцев вперед, спросит,

почему мы не можем проделать то же самое в отношении атмосферы.

Ведь это всего лишь другая система потоков и ее законы не более

сложны. Но я понял, что любая физическая система, не проявляющая

периодичности в поведении, непредсказуема

Модель Лоренца не представляет какого-то реального феномена

погоды, но служит поразительным примером того, как простой набор

нелинейных уравнений может привести к крайне сложному поведению.

Публикация этой модели в 1963 году знаменовала зарождение теории

хаоса, и аттрактор, известный с тех пор как аттрактор Лоренца, стал самым

известным и широко изучаемым из странных аттракторов. В то время как

аттрактор Уэда двухмерен, аттрактор Лоренца расположен в трех

измерениях (рис. 6-11). Вычерчивая его, точка в фазовом пространстве

движется по видимости случайным образом и описывает несколько

колебаний нарастающей амплитуды вокруг одного центра, затем следуют

колебания вокруг второго центра, потом она внезапно возвращается и

осциллирует вокруг первого центра и т. д.

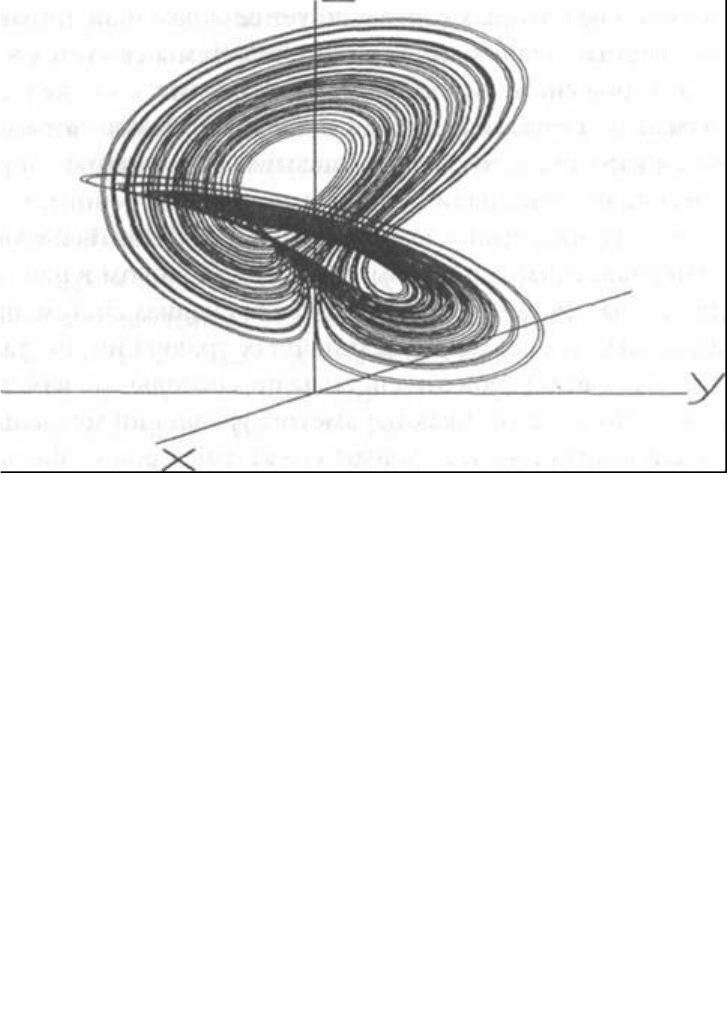
Рис. 6-11. Аттрактор Лоренца. Из Mosekilde et al. (1994)

От количества к качеству

Невозможность предсказать, какую точку в фазовом пространстве

пересечет траектория аттрактора Лоренца в определенный момент

времени, являет собой общую для хаотических систем особенность.

Однако это вовсе не означает, что теория хаоса не дает оснований никаким

предсказаниям. Возможны чрезвычайно точные прогнозы относительно

качественных особенностей поведения системы, а не точных значений ее

переменных в определенный момент времени. Новая математика, таким

образом, представляет сдвиг от количества к качеству, что характерно Для

системного мышления вообще. В то время как традиционная математика

имеет дело с количествами и формулами, теория динамических систем

связана с качеством и паттерном.

Действительно, анализ нелинейных систем с помощью топологических

характеристик их аттракторов известен как количественный анализ. У

нелинейной системы может быть несколько аттракторов разных типов, как

хаотичных, или «странных», так и нехаотичных. Все траектории,

начинающиеся в определенной области фазового пространства, рано или

поздно приводят к одному и тому же аттрактору. Эта область называется

сферой притяжения данного аттрактора. Таким образом, фазовое

пространство нелинейной системы разбивается на несколько сфер

притяжения, каждой из которых соответствует ее отдельный аттрактор.

Количественный анализ динамической системы сводится к

определению аттракторов системы и сфер их притяжения, а также

классификации их в рамках топологических характеристик. Результатом

является динамическая картина всей системы, называемая фазовым

портретом. Математические методы анализа фазовых портретов основаны

на новаторских трудах Пуанкаре; впоследствии они были развиты и

усовершенствованы американским топологом Стивеном Смейлом в начале

60-х

. Смейл использовал свой метод не только для анализа систем,

представленных определенным набором нелинейных уравнений, но также

для изучения того, как ведут себя эти системы при небольших изменениях

в их уравнениях. По мере того как параметры уравнений медленно

меняются, фазовый портрет — т. е. формы его аттракторов и сферы

притяжения — как правило, претерпевает соответствующие плавные

изменения, не изменяя своих основных характеристик. Смейл использовал

термин «структурно устойчивый» для описания таких систем, в которых

небольшие отклонения в уравнениях не изменяют основного характера

фазового портрета.

Во многих нелинейных системах, однако, малые изменения в

определенных параметрах могут обусловить серьезные изменения

основных характеристик фазового портрета. Аттракторы могут исчезнуть

или превратиться из одного в другой, могут также внезапно появиться

новые аттракторы. Говорят, что такие системы структурно неустойчивы, и

критические точки неустойчивости называют точками бифуркации

(«разветвления»), поскольку в эволюции системы именно в этих местах

внезапно появляется «вилка», и система отклоняется в том или ином новом

направлении. В математическом смысле, точки бифуркации отмечают

внезапные изменения фазового портрета системы. В физическом смысле,

они соответствуют точкам неустойчивости, в которых система резко

изменяется, и неожиданно появляются новые формы упорядоченности.

Как показал Пригожий, такие неустойчивости случаются только в

открытых системах, далеких от равновесия

Поскольку типов аттракторов достаточно мало, то не много существует

и различных типов бифуркации; следовательно, их можно

классифицировать топологически, как и аттракторы. Одним из первых, кто

в 70-е годы осуществил это, был французский математик Рене Том; он

использовал термин катастрофы вместо бифуркации и определил семь

элементарных катастроф

. В настоящее время математикам известно

примерно в три раза больше типов бифуркаций. Ральф Эбрахам, профессор

математики в Калифорнийском университете в Санта-Круз, вместе с

художником-графиком Кристофером Шоу создали серию книг по

визуальной математике без единого уравнения или формулы; авторы

считают эти книги началом полной энциклопедии бифуркаций

Фрактальная геометрия

В то время как в течение 60-х и 70-х гг. ученые исследовали странные

аттракторы, независимо от теории хаоса была изобретена фрактальная

геометрия, давшая мощный математический язык для описания тонкой

структуры хаотических аттракторов. Автором этого нового языка стал

французский математик Бенуа Мандельбро. В конце 50-х Мандельбро

начал изучать геометрию самых разнообразных нерегулярных

естественных феноменов, а в 60-е годы он осознал, что у всех

рассматриваемых им геометрических форм есть поразительные общие

особенности. В последующие десять лет Мандельбро разрабатывал новый

тип математики, чтобы описать и проанализировать эти особенности. Он

ввел термин фрактал, характеризующий его изобретение, и опубликовал

свои результаты в замечательной книге «Фрактальная геометрия

природы». Книга имела огромное влияние на новое поколение

математиков, развивавших теорию хаоса и другие разделы теории

динамических систем

Недавно в одной из бесед Мандельбро пояснил, что фрактальная

геометрия имеет дело с тем аспектом Природы, который каждому

известен, но который никто еще не смог описать в формальных

математических терминах

. Некоторые природные характеристики

геометричны в традиционном смысле. Ствол дерева более или менее

подобен цилиндру; полная Луна более или менее напоминает круглый

диск; планеты движутся вокруг Солнца по более или менее эллиптическим

траекториям. Однако это исключения, и Мандельбро напоминает нам:

Чаще всего природа в высшей степени сложна. Как описать облако?

Облако — это не сфера... Оно похоже на мяч, но очень

неупорядоченно. А гора? Гора — не конус... Если вы хотите говорить

о горах, реках, молнии, геометрический школьный язык оказывается

совершенно неадекватным.

И Мандельбро создал фрактальную геометрию — «язык, на котором

можно говорить об облаках», — чтобы описывать и анализировать

сложность нерегулярных форм в окружающем нас мире природы.

Наиболее поразительное свойство этих «фрактальных» форм

заключается в том, что их характерные паттерны многократно

повторяются на нисходящих уровнях так, что их части на любом уровне по

форме напоминают целое. Мандельбро иллюстрирует это свойство

самоподобия, отламывая кусочек цветной капусты и указывая на то, что

сам по себе кусочек выглядит как маленький кочан цветной капусты

. Он

продолжает демонстрацию, деля часть дальше, изымая еще один кусочек,

который тоже выглядит как очень маленький кочан. Таким образом,

каждая часть выглядит как целый овощ. Форма целого подобна самой себе

на всех уровнях выбранного диапазона.

В природе встречается множество других примеров самоподобия.

Камни в горах напоминают маленькие горы; ответвления молнии или края

облаков снова и снова повторяют один и тот же паттерн; побережье моря

можно делить на все более мелкие части, и в каждой из них будут

проявляться подобные друг другу очертания береговой линии.

Фотографии дельты реки, кроны дерева или ветвления кровеносных

сосудов могут проявлять паттерны такого разительного сходства, что мы

порой не можем отличить один от другого. Подобие образов совершенно

различных масштабов было известно очень давно, но до Мандельбро

никто не владел математическим языком для описания этого явления.

Когда в середине 70-х Мандельбро опубликовал свою новаторскую

книгу, он еще сам не догадывался о связи между фрактальной геометрией

и теорией хаоса, но ему и его коллегам-математикам не понадобилось

много времени, чтобы обнаружить, что странные аттракторы могут

служить изысканнейшими примерами фракталов. Если части их структуры

увеличить, то обнаруживается многослойная субструктура, в которой

вновь и вновь повторяются одни и те же паттерны. В связи с этим

странные аттракторы стали определять как траектории в фазовом

пространстве, в которых проявляются черты фрактальной геометрии.

Еще одна важная связь между теорией хаоса и фрактальной геометрией

проявилась в переходе от количества к качеству. Как мы видели,

невозможно предсказать значения переменных хаотической системы в

определенный момент времени, но можно предсказать качественные

особенности поведения системы. Точно так же, невозможно вычислить

длину или площадь фрактальной формы, однако можно — качественным

способом — определить степень ее изрезанности.

Мандельбро подчеркнул эту существенную особенность фрактальных

форм, задав провоцирующий вопрос: какова протяженность побережья

Британии? Он показал, что, поскольку измеряемую длину можно

растягивать до бесконечности, переходя ко все более мелкому масштабу,

на этот вопрос нет однозначного ответа. Зато можно определить число в

диапазоне от 1 до 2, которое характеризует изрезанность побережья. Для

британского побережья это число равно около 1,58; для более изрезанного

норвежского берега оно близко к 1,7027.

Поскольку можно показать, что это число имеет определенные свойства

размерности, Мандельбро назвал его фрактальной размерностью. Мы

можем понять эту идею интуитивно, зная, что извилистая линия занимает

больше пространства на плоскости, чем одномерная гладкая линия, но

меньше, чем сама двухмерная плоскость. Чем больше изрезана линия, тем

ближе к числу 2 ее фрактальная размерность. Подобным же образом,

скомканный лист бумаги занимает больше пространства, чем плоскость,

но меньше, чем сфера. Таким образом, чем плотнее скомкана бумага, тем

ближе к числу 3 будет ее фрактальная размерность.

Концепция фрактальной размерности, изначально появившаяся как

чисто абстрактная математическая идея, превратилась со временем в

мощный инструмент анализа сложности фрактальных форм, поскольку

замечательно соответствует нашему жизненному опыту. Чем более

изрезаны очертания молнии или границы облаков, чем менее сглажены

формы побережий или гор, тем выше их фрактальные размерности. Чтобы

смоделировать фрактальные формы, встречающиеся в природе, можно

сконструировать геометрические фигуры, обладающие точным

самоподобием. Основным методом для построения таких математических

фракталов служит итерация, т. е. многократное повторение определенной

геометрической операции. Процесс итерации, который привел нас к

преобразованию пекаря — математической операции, лежащей в основе

странных аттракторов, — оказался, таким образом, главной

математической особенностью, объединяющей теорию хаоса с

фрактальной геометрией.

Одной из простейших фрактальных форм, производимых итерацией,

является так называемая кривая Коха, или «кривая снежинки»

Геометрическая операция заключается в том, чтобы разбить отрезок линии

на три равные части и затем заменить центральную секцию двумя

сторонами равностороннего треугольника, как показано на рис. 6-12.

Повторение этой операции во все более мелких масштабах приводит к

появлению кружевной снежинки (рис. 6-13). Как и в случае с изрезанной

береговой линией, кривая Коха становится бесконечно длинной, если

итерация продолжается бесконечно. В сущности, кривую Коха можно

рассматривать как очень грубую модель береговой линии (рис. 6-14).

Рис. 6-14. Моделирование береговой линии с помощью кривой Коха

Математика сложных систем

С помощью компьютеров простые геометрические итерации можно

применять тысячи раз в различных масштабах, производя так называемые

фрактальные подделки — компьютерные модели растений, деревьев, гор,

береговых линий и т. п., обладающие поразительным сходством с

реальными формами, которые встречаются в природе. На рис. 6-15

приведен пример такой подделки. Производя итерацию над простым

рисунком веточки в различных масштабах, удалось получить красивое и

сложное изображение папоротника.

Рис. 6-15. Фрактальная подделка папоротника. Из Garcia (1991)

Этот новый математический аппарат позволил ученым строить точные

модели разнообразных нерегулярных естественных форм. Занимаясь этим

моделированием, они повсеместно обнаруживали присутствие фракталов.

Фрактальные паттерны облаков, которые изначально воодушевили

Мандельбро на поиски нового математического языка, вероятно, самые

изумительные. Их самоподобие охватывает семь порядков величин, а это

означает, что если границу облака увеличить в 10 000 000 раз, она будет

иметь все ту же знакомую форму.

Комплексные числа

Вершиной фрактальной геометрии стало открытие Мандельбро

математической структуры, которая обладает ошеломляющей сложностью

и все же может быть воспроизведена с помощью очень простой

итеративной процедуры. Чтобы понять эту поразительную фрактальную

фигуру, известную как множество Мандельбро, необходимо сначала

ознакомиться с одним из важнейших математических понятий —

комплексными числами.

Открытие комплексных чисел стало восхитительной главой в истории

математики

. Когда в средние века возникла алгебра и математики

принялись исследовать все виды уравнений и классифицировать их

решения, они вскоре столкнулись с задачами, не имевшими решения в

рамках множества известных им чисел. В частности, уравнения типа х + 5

= 3 заставили их расширить понятие числа до отрицательных чисел, так

чтобы решение могло быть записано как х = -2. В дальнейшем так

называемые действительные числа — положительные и отрицательные

целые числа, дроби и иррациональные числа (например, квадратные корни

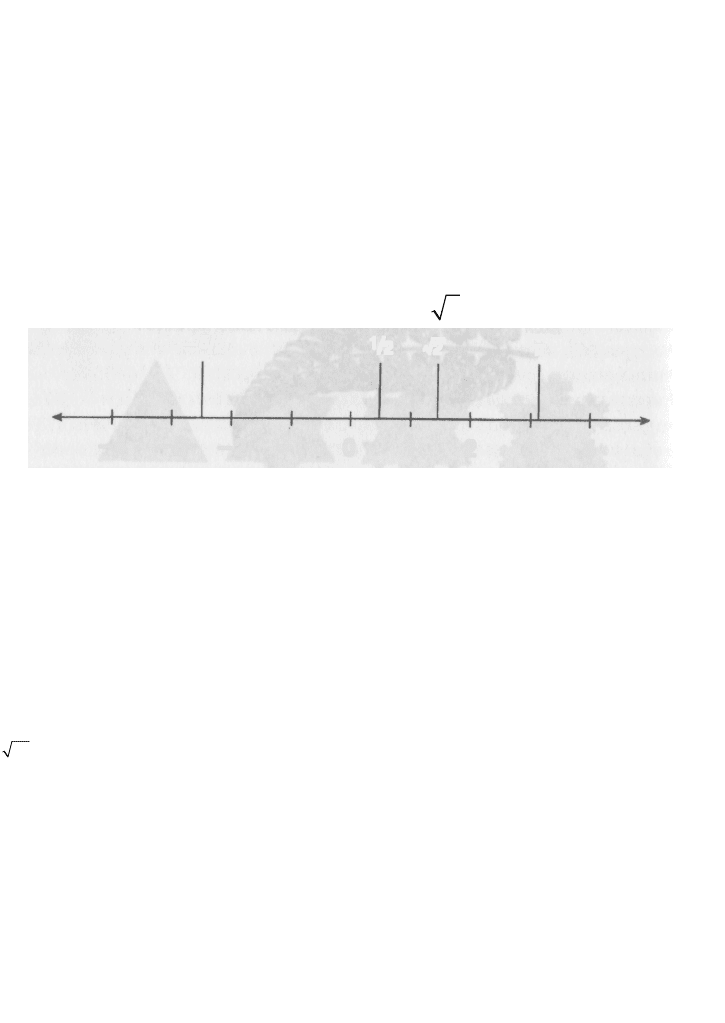
или знаменитое число п) — стали представлять как точки на единой

плотно населенной числовой оси (рис. 6-16).

/2 1/2

-4 -3 -2 -1 0 1 2 3 4

Рис. 6-16 Числовая ось

С таким расширением понятия числа все алгебраические уравнения, в

принципе, могли быть решены — за исключением тех, где фигурировали

квадратные корни отрицательных чисел. Уравнение х

= 4 имеет два

решения: х = 2 и х = -2; однако для х

= -4, по всей видимости, не должно

быть решения, поскольку ни +2, ни - 2 при возведении в квадрат не дадут -

Древние индийские и арабские алгебраисты постоянно встречались с

такими уравнениями, но отказывались даже записывать выражения типа

4

, считая их абсолютно бессмысленными. И только в XVI веке

квадратные корни отрицательных чисел стали появляться в

алгебраических текстах, но и тогда авторы спешили пояснить, что такие

выражения на самом деле ничего не означают.

Декарт называл квадратный корень отрицательного числа «мнимым

числом» и был уверен, что появление таких мнимых чисел в расчетах

означает, что проблема неразрешима. Другие математики использовали

термины «фиктивные», «фальшивые» или «невозможные» для

обозначения величин, которые сегодня мы, с легкой руки Декарта, все еще

называем мнимыми числами.

Поскольку квадратный корень отрицательного числа не может быть