Калабухов Е.В. Курс лекций по дисциплине Базы данных, знаний и экспертные системы
Подождите немного. Документ загружается.

R
ABC
123
124
210
323
ABC
123
124
)(
1
R
A=
σ
Рисунок 11. Выборка.
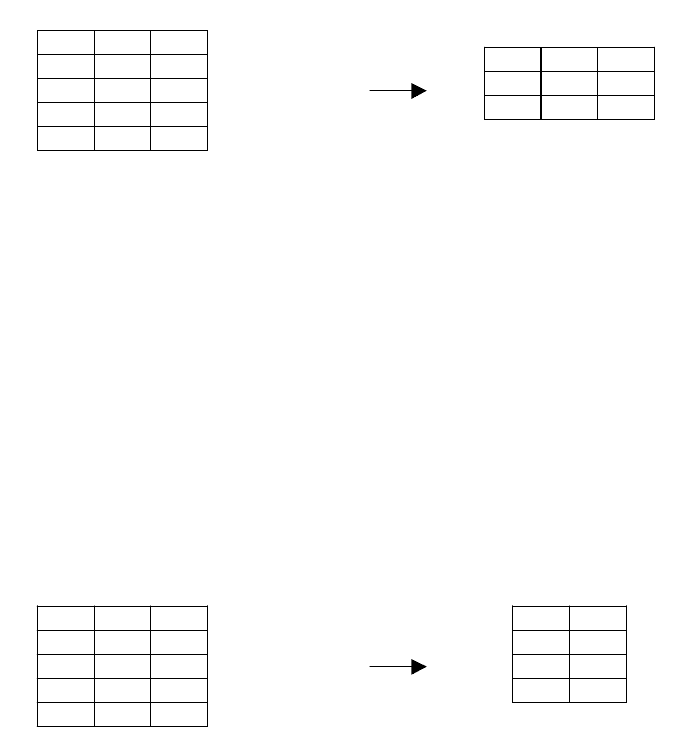
2) Проекция (projection) – унарная операция, определяет новое
отношение, содержащее вертикальное подмножество отношения R,
создаваемое посредством извлечения значений указанных атрибутов и
исключения из результата строк-дубликатов (кортежей-дубликатов):
)(
,,2,1
R
AnAA L
∏
, где (A1, A2, …, An) – имена атрибутов.
R
ABC
123
124
210
323
AB
12
21
32
)(
,
R
BA
∏
Рисунок 12. Проекция.
3) Декартово произведение (cartesian product) – определяет новое
отношение, которое является результатом сцепления (конкатенации) каждого
кортежа из отношения R с каждым кортежем из отношения S. Если одно
отношение имеет I кортежей и N атрибутов, а другое – J кортежей и M
атрибутов, то отношение их с декартовым произведением будет содержать (I*J)
кортежей и (N+M) атрибутов. Если исходные отношения содержат атрибуты с
одинаковыми именами, то для обеспечения уникальности имен атрибутов в
отношении они будут переименованы (обычно включая имя отношения как
префикс):
S
R
× , где R и S – имена отношений.
71
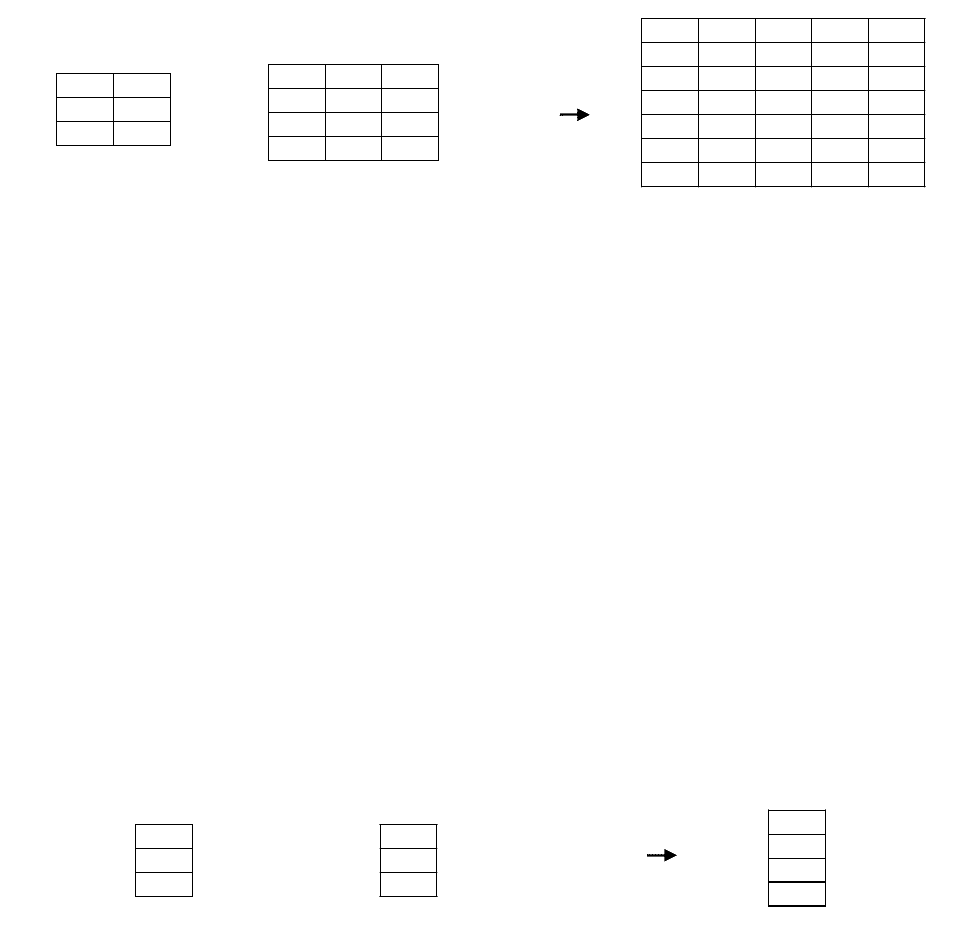
S
A B C
1 0 1
1 1 2
3 5 1
R
A B
1 0
1 1
SR ×
R.A R.B S.A S.B S.C
1 0 1 0 1
1 0 1 1 2
1 0 3 5 1
1 1 1 0 1
1 1 1 1 2
1 1 3 5 1
Рисунок 13. Декартово произведение.
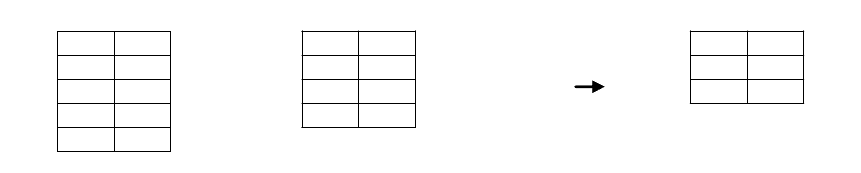
4) Объединение (union) – определяет новое отношение, которое является
результатом сцепления (конкатенации) кортежей отношений R и S, и
исключения в полученном отношении кортежей-дубликатов. Отношения R и S
должны быть совместимы по объединению, т.е. они должны иметь одинаковое
количество атрибутов, причем парные атрибуты (совмещающиеся при склейке)
должны быть определены на одном домене. Если исходные отношения
содержат I и J кортежей, то результирующее отношение будет содержать
максимум (I+J) кортежей:
S
R
∪ , где R и S – имена отношений.
R
A
1
2
SR ∪
S
A
1
3
A
1
2
3
Рисунок 14. Объединение.
5) Разность (set difference) – определяет новое отношение, которое
состоит из кортежей, которые имеются в отношении R, но отсутствуют в
отношении S. При этом отношения R и S должны быть совместимы по
объединению:
S
R
− , где R и S – имена отношений.
72
R
A B
1 1
1 2
2 3
2 4
SR −
S
A B
1 1
2 3
4 4
A B
1 2
2 4
Рисунок 15. Разность.
Дополнительные операции реляционной алгебры:
6) Операции соединения (join) – одна из самых важных операций
реляционной алгебры (является производной от операции декартова
произведения, наиболее трудоемкая операция (трудно реализуется и малая
производительность)). Типы операций соединения:
- Тета-соединение (Θ-join) – определяет отношение, которое содержит
кортежи из декартова произведения отношений R и S, удовлетворяющие
предикату F. Предикат F имеет вид
ii
bSaR ..
Θ
, где вместо Θ может быть указан
один из операторов сравнения (<, <=, >, >=, = или ~=):
)( SRSR
FF
×=
σ
><
.
Степень Θ-соединения – сумма степеней операндов.
- Если предикат F содержит только оператор равенства (=), то такое тета-
соединение называется соединением по эквивалентности (equal-join).
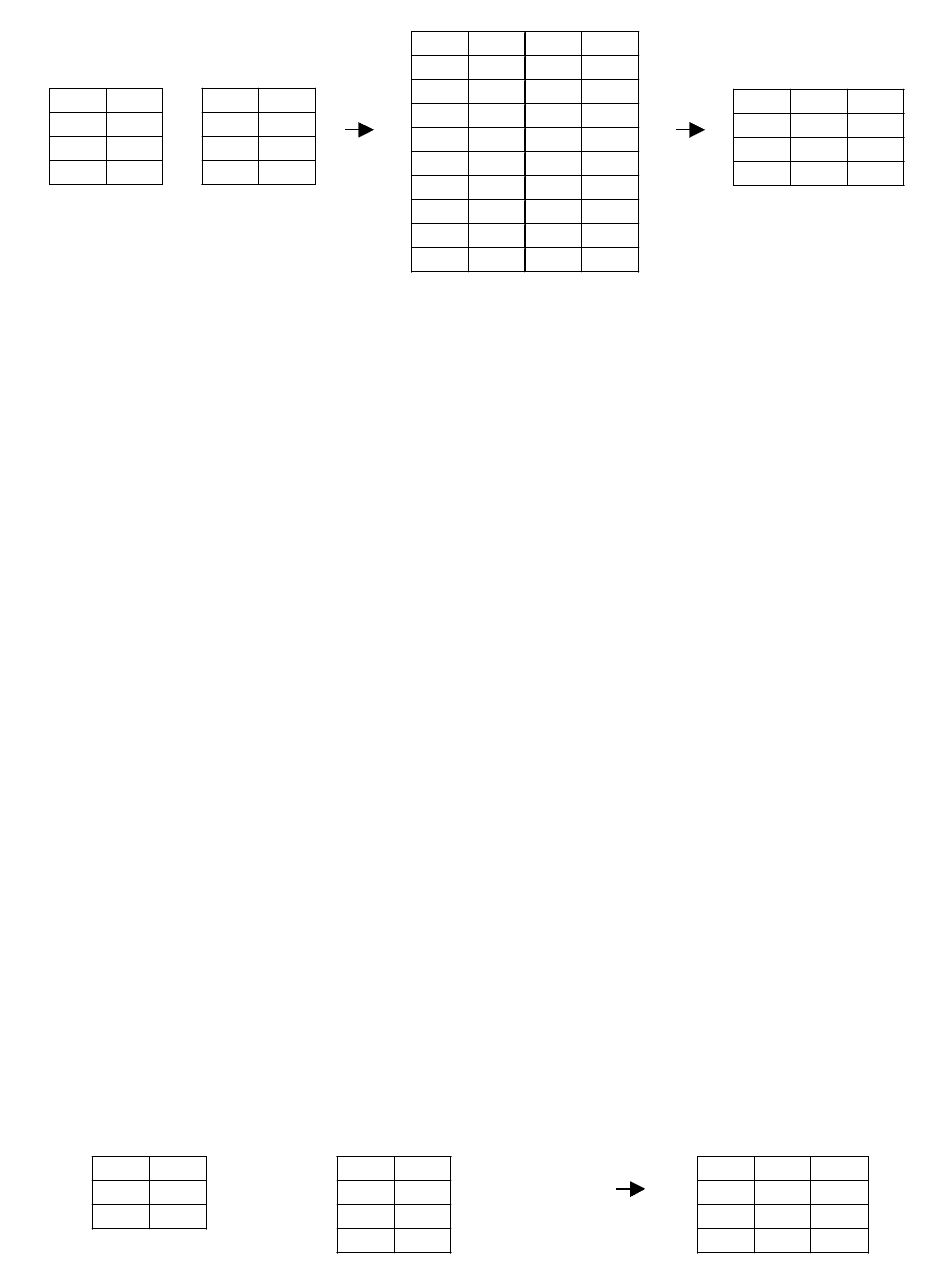
- Естественное соединение (natural join) – соединение по эквивалентности
двух отношений R и S, выполненное по всем общим атрибутам x, из
результатов которого исключается по одному экземпляру каждого общего
атрибута. Степень естественного соединения равна сумме степеней операндов
отношений R и S минус количество общих атрибутов x (если отношения R и S
не имеют общих имен атрибутов, то естественное соединение эквивалентно
декартову произведению):
S
R
>< , где R и S – имена отношений.
73
R
AB
12
15
36
S
A С
10
27
35
SR ><
ABC
120
150
365
SR
×
R.A B S.A C
1210
1227
1235
1510
1527
1535
3610
3627
3635
Рисунок 16. Естественное соединение.
- Внешнее соединение (outer join) - три вида:
-- левое внешнее соединение – соединение, при котором кортежи
отношения R (находящегося в выражении слева), не имеющие совпадающих
значений в общих столбцах отношения S (находящегося в отношении справа),
также включаются в результирующее отношение (отсутствующие значения
заменяются определителем NULL; в таком соединении сохраняются кортежи,
которые были бы утрачены при использовании других типов соединения):
S
R
<⊃ , где R и S – имена отношений.
-- правое внешнее соединение – соединение, при котором кортежи
отношения S (находящегося в выражении справа), не имеющие совпадающих
значений в общих столбцах отношения R (находящегося в отношении слева),
также включаются в результирующее отношение (отсутствующие значения
заменяются определителем NULL):
S
R
⊂> , где R и S – имена отношений.
R
AB
11
23
SR <
⊃
S
BC
1X
1Y
2Z
ABC
11X
11Y
23null
Рисунок 17. Левое внешнее соединение.
-- полное внешнее соединение – соединение, при котором кортежи
74

отношения R (находящегося в выражении слева), не имеющие совпадающих
значений в общих столбцах отношения S (находящегося в отношении справа), а
также кортежи отношения S (находящегося в выражении справа), не имеющие
совпадающих значений в общих столбцах отношения R (находящегося в
отношении слева), также включаются в результирующее отношение
(отсутствующие значения заменяются определителем NULL):
S
R
⊃⊂ , где R и S – имена отношений.
- Полусоединение (semi join) – определяет отношение, которое содержит
те кортежи отношения R, которые входят в соединение отношений R и S:
)( SRSR
FAF
><>
∏
=
, где A – множество всех атрибутов в отношении
R.
7) Пересечение (intersection) – определяет отношение, которое содержит
кортежи, присутствующие как в отношении R, так и в отношении S (отношения
R и S должны быть совместимы по объединению):
)(
S
R
R
S
R
−
−
=∩ , где R и S – имена отношений.
8) Деление (division) – определяет отношение, которое содержит набор
кортежей отношения R, определенных на множестве атрибутов C, которые
соответствуют комбинации всех кортежей отношения S:
)))((()( RRSRSR
CCC
−
∏
×
∏−∏=÷
, где R и S – имена отношений.
R
AB
X1
X2
Y1
Y2
Z1
S
R
÷
S
B
1
2
A
X
Y
Рисунок 18. Деление.
Операции выборки, проекции, декартова произведения, объединения и
разности – примитивные операции (их нельзя выразить через другие операции
реляционной алгебры).
75
Операции соединения, пересечения и деления – не примитивные (т.е. их
можно выразить через основные операции), но т.к. эти операции на практике
часто используются, то они выделены в отдельную группу (чтобы не выражать
их каждый раз – что-то типа макросов).
Цель реляционной алгебры – запись выражений для:
•
определения области выборки – определение данных для их выбора;
•
определение области обновления – определение данных для их вставки,
изменения или удаления;
• определения представлений и снимков – определение данных для
представления в виде некоторого отношения;
•
определение правил безопасности – определение данных, для которых
осуществляется контроль доступа;
•
определение требований устойчивости – определение данных, которые
входят в область для некоторых операций управления одновременным
доступом;
•
определение правил корпоративной целостности.
4.3.3.3.2. Реляционное исчисление
Реляционное исчисление происходит от части символьной логики,
которая называется исчислением предикатов.
Предикат (в логике первого порядка или теории исчисления предикатов)
– истинностная функция с аргументами (при подстановке вместо аргументов
значений эта функция становится выражением, называемым суждением,
которое может быть истинным или ложным).
Если предикат содержит переменную (например, «x является студентом
этой группы»), то у этой переменной должна быть соответствующая область
определения (при подстановке одних значений из ее области определения
суждение может быть истинным, а при подстановке других - ложным).
76
Если P – предикат, то множество всех значений переменной x, при
которых P становится истинным:
{}
)(| xPx
.
Предикаты могут соединяться с помощью логических операторов
∧
(AND), (OR) и ~ (NOT) (при этом образуются составные предикаты).
∨
Реляционное исчисление существует в двух формах:
1) Реляционное исчисление кортежей (Кодд).
Задача реляционного исчисления кортежей – нахождение таких кортежей,
для которых предикат является истинным.
Реляционное исчисление кортежей основано на переменных кортежа –
переменные, областью определения которых является указанное отношение и
допустимыми значениями могут быть только кортежи данного отношения.
Предикат P называется формулой (в математической логике – правильно
построенной формулой (WFF – well formed formula)).
Для указания количества экземпляров (кортежей), к которым может быть
применен предикат, в формулах могут использоваться два вида кванторов:
•
квантор существования (
∃
- «существует») – означает, что в отношении
есть хотя бы один кортеж, для которого формула – истинна;
•
квантор общности (
∀
- «для всех») – означает, что формула будет
истинна только для всех кортежей отношения.
Переменные кортежа называются свободными, если они не
квалифицируются кванторами
∃
и
∀
, иначе они называются связанными
переменными.
В реляционном исчислении не каждая последовательность формул
является допустимой (т.е. не двусмысленной и не бессмысленной). Правила
построения WFF:
•
если P является n-арной формулой (предикатом с n аргументами), а t1, t2,
…, tn – это константы или переменные, то выражение P(t1, t2, …, tn) –
правильно построенная формула;
77
• если t1 и t2 – константы или переменные из одного домена, а Θ
представляет собой один из операторов сравнения (<, <=, >, >=, =, ~=), то
выражение t1Θt2 – правильно построенная формула;
•
если выражения F1 и F2 – формулы, то их конъюнкция (логическое «И»)
означается как
21
F
F
∧
, дизъюнкция (логическое «ИЛИ») -
21
F
F
∨
, а
отрицание - ~F1;
•
если выражение F1 является формулой со свободной переменной X, то
выражения и )
)(XF∃ (XF
∀
- также являются формулами;
•
все результирующие значения должны входить в область определения
формулы (обычно область определения задается как RANGE OF
переменная_кортежа IS имя_отношения1
(выражение_исчисления_кортежей1), имя_отношения2
(выражение_исчисления_кортежей2), … (замечание: все отношения при
этом должны иметь идентичные заголовки)).
Например, есть два отношения SN(S#, NAME, CITY, G#) – данные о
студенте и SG(G#, NAME, CITY) –данные о группе:
1) RANGE OF N IS SN, {N | N.S# > 1000} – получить значения всех
кортежей (N – переменная кортежа, содержит текущий кортеж определенный
на отношении SN в текущее время), значение атрибута S# у которых больше
1000;
2) RANGE OF N IS SN, RANGE OF G IS SG, {N.NAME, N.CITY |
∃
G
(G.G# = N.G# G.NAME = “012345”)} – получить имя студента и город
(значения NAME и CITY отношения SN), если есть хотя бы один кортеж
отношения SG, в котором значение атрибута G# равно значению G# в текущем
кортеже N и номер группы GROUP = «012345»;
∧
3) RANGE OF N IS SN, RANGE OF G IS SG, {N.NAME | G (G.CITY ~=
N.CITY)} – получить имена студентов, город проживания которых не совпадает
с расположением ни одной группы (что эквивалентно {N.NAME | ~
∀
∃
G (G.CITY
= N.CITY)}).
Опасные формулы – формулы без ограничения диапазона возможных
78
значений кортежей (при этом может быть получена бесконечная
последовательность кортежей, что недопустимо).
2) Реляционное исчисление доменов (Лакруа и Пиро).
В реляционном исчислении доменов используются переменные, значения
которых берутся из доменов (а не из кортежей отношений). Если P(a1 : d1, a2 :
d2, …, an : dn) – предикат с переменными домена d1, d2, …, dn (определенными
на атрибутах a1, a2, …, an соответственно), то множество переменных домена,
для которых предикат истинен:
{d1, d2, …, dn | P(a1 : d1, a2 : d2, …, an : dn)}.
Задача реляционного исчисления доменов – проверить условие
принадлежности, чтобы определить, принадлежат ли значения указанному
отношению (например, выражение R(x : rx, y : “y1”) считается истинным тогда
и только тогда, когда в отношении R имеется кортеж со значениями rx
(переменная домена – содержит текущее значение атрибута) и “y1”(литерал -
константа) в его атрибутах x и y соответственно.
Например, есть отношение SN(S#, NAME, RATING) – данные о студенте:
{N | R (SN (NAME : N, RATING : R)
∃
∧
R > 7.8)} – получить значения
всех студентов с рейтингом больше 7,8 (проверка существует ли кортеж с
атрибутами NAME (переменная N) и RATING (переменная R) в отношении SN,
причем значение атрибута RATING в этом кортеже > 7,8).
Если формулы безопасны, то реляционное исчисление доменов
семантически эквивалентно реляционному исчислению кортежей.
4.3.3.3.3. Связь реляционного исчисления и реляционной алгебры
Существует алгоритм («алгоритм редукции Кодда»), с помощью которого
выражение реляционного исчисления (кортежей) можно преобразовать в
семантически эквивалентное выражение реляционной алгебры (т.е.
79
реляционная алгебра и реляционное исчисление эквивалентны – каждому
выражению в реляционной алгебре соответствует эквивалентное выражение в
исчислении, и наоборот).
Так как реляционное исчисление носит описательный характер
(описывает, что надо получить) – ближе к естественным языкам, а реляционная
алгебра носит предписывающий характер (указывает, каким образом (как)
должен быть получен результат) – ближе к машинным языкам, и между ними
есть однозначное соответствие, то возможна компьютерная обработка запросов
написанных с помощью реляционного исчисления (запрос берется у
пользователя как выражение исчисления (легче описывается), к этому запросу
применяется алгоритм редукции и вычисляется полученное реляционное
выражение (+ оптимизация)).
Реляционно полный язык – язык по своим возможностям не уступающий
реляционному исчислению или реляционной алгебре (т.е. реализующий
операции эквивалентные основным операциям реляционной алгебры).
Желательно чтобы в таком языке была и вычислительная полнота (наличие
большинства вычислимых функций (+, -, * и т.п.)).
4.3.3.4. Перевод ER-диаграммы в реляционную модель данных
Преобразование ER-диаграммы в реляционную модель (схему) позволяет
выполнить переход от концептуальной фазы проектирования к логической.
Алгоритм преобразования следующий:
1)
Каждая простая сущность (объект на ER-диаграмме) превращается в
таблицу. Простая сущность - сущность, не являющаяся подтипом и не
имеющая подтипов. Имя сущности становится именем таблицы.
2)
Каждый атрибут становится возможным столбцом с тем же именем; при
этом может выбираться более точный формат. Столбцы,
соответствующие необязательным атрибутам, могут содержать
80
