Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves

Подождите немного. Документ загружается.

364

5 Epilogue

For conventional gravity waves, the Reynolds number (R) is typically

quite large: anywhere from about 10

upwards, and for deep water this

could be much larger. Thus the approximation of interest to us is

described by R -> oo; under this limiting process we find (Q5.1) that

(5.22)

where we have chosen the waves to be right-running (and hence the

positive square root is taken). The leading term is our very familiar result

for the propagation speed of (inviscid) gravity waves, first given in equa-

tion (2.13). The viscous contribution in (5.22), which is provided by the

term in l/VR, possesses both real and imaginary parts and therefore

affects the speed of the wave as well as its attenuation. The decay of

the harmonic wave, in this approximation, is controlled by the negative

exponent proportional to

(8k)

5/4

sech

5/4

8k cosech

3/4

(5.23)

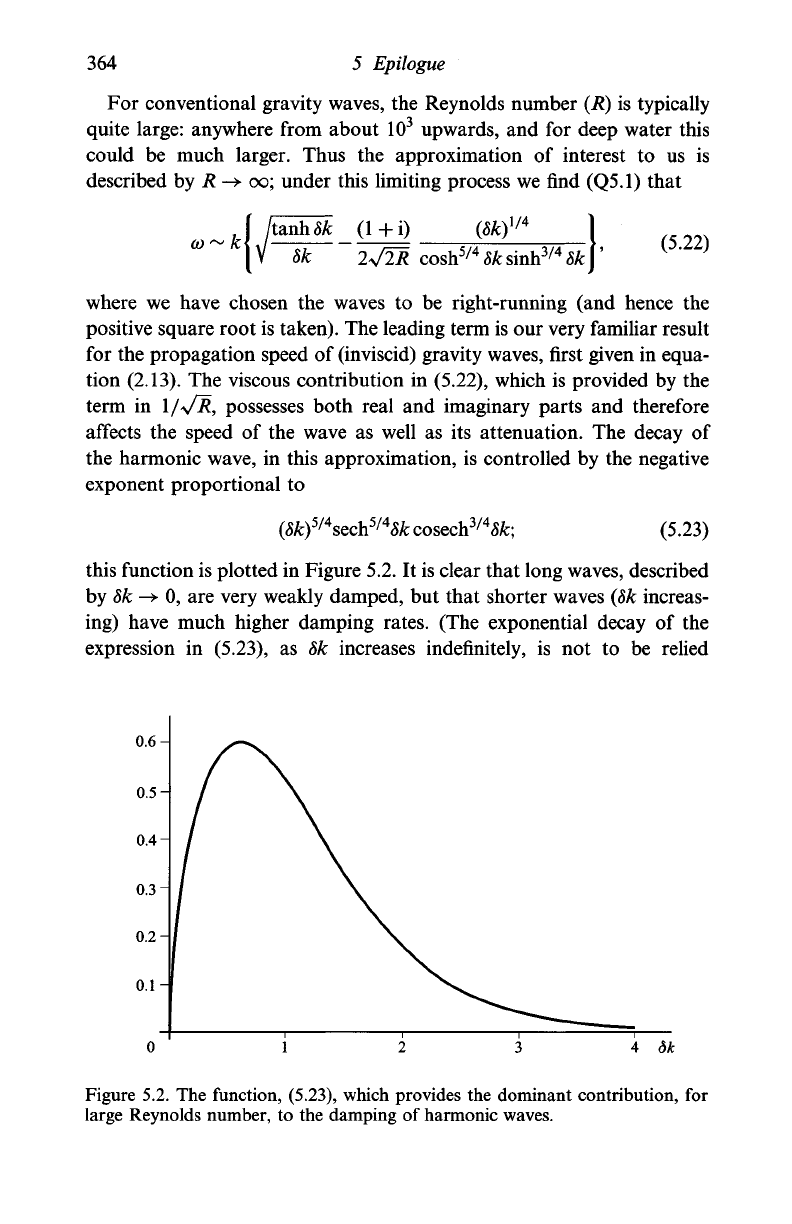
this function is plotted in Figure 5.2. It is clear that long waves, described

by 8k -> 0, are very weakly damped, but that shorter waves (8k increas-

ing) have much higher damping rates. (The exponential decay of the

expression in (5.23), as 8k increases indefinitely, is not to be relied

4 dk

Figure 5.2. The function, (5.23), which provides the dominant contribution, for

large Reynolds number, to the damping of harmonic waves.

Applications

the propagation

of gravity

waves

365

upon, since the argument underpinning (5.22) was R -> oo at 8k fixed; a

different asymptotic structure appears for 8k -> oo and, indeed, probably

we should then include the surface tension contribution; see Q5.4.) The

damping rate of shorter, as compared with longer, waves provides the

explanation for the limited distances over which capillary waves are seen

to survive, as compared with gravity waves (as we commented in Section

2.1.2). Other approximations and interpretations of the dispersion

relation, (5.21), can be found in the exercises at the end of this chapter.

5.2.2 Attenuation of the solitary wave

In Section 2.9 we quoted Russell's description of

his

chase, on horseback,

of a solitary wave; his evidence, and much that has been collected since

his time, indicates that the solitary wave is only very weakly affected by

viscosity. We shall study the way in which the viscous effects, as described

by the Navier-Stokes equations, provide a slow evolution of the solitary

wave. This

shall do using the

method

multiple

scales, the scales being

associated with the propagation of the wave, the nonlinear evolution of

the wave, and the evolution on a viscous scale.

We start with the equations given in Section 5.1, (5.1)—(5.7), but intro-

duce the transformation which describes the scales on which a KdV-type

balance occurs, as s -> 0 for

arbitrary

these are (cf. equations (3.10),

(3.11))

8 8 s

x-*-u2

t-^-m^ w->—w.

The equations are therefore

1 .

+ s(uu

+ wu

) = -p

s{w

+ s(uw

+ ww

)} = -p

+ — (w

);

+ w

= 0,

with

p-rj-

2— [w

- erj

+ sw

) + 8

}/(l +

)

= 0;

(1 -

)(u

+ ew

) + 2e

- u

)rj

= 0;

w = r\

+ £urj

z =

er\

366 5 Epilogue

and

u = w =

on z = 0.

Now, in the derivation of

the

KdV equation, we introduced the variables

see equations (3.17) and (3.18). Here we follow essentially the same route,

but include evolution on a suitable (slow) viscous scale and also allow the

nonlinear contribution to the speed of the wave to vary on this same

scale. (We have already seen that the speed of harmonic waves is altered

by the presence of a viscous ingredient; see equation (5.22).) Thus, antici-

pating a KdV-type of equation with independent variables r and £ in the

absence of viscosity, we introduce a slow evolution of this system in the

form

= st, T = Ar = eAt, £ = x - t - ^ /

c(T')dT\

(5.24)

where we shall treat £, r and T as independent variables (the method of

multiple scales), and where A is yet to be chosen. Different problems

require different choices of A, in terms of

e (-• 0) and r =

l/R^/e

(-* 0),

which we treat as independent parameters. Under this transformation our

governing equations become

+ eAu

ec)u{:

+ e(uu% +

) —

-p^ + r(u

+ eu^)\ (5.25)

e{sw

+ eAw

sc)w^

e(uw%

)}

= -p

er(w

+ ew^)\

(5.26)

U£

+ w

(5.27)

with

p-rj-

2er{w

- e^(u

+ ew£ + s

^}/(l + s

^) = 0;

(1 -

rjl)(u

)

+ 2s\w

- u^ = 0;

= 1 +

BY]

w = £r)

+ £Arj

-(1

(5.28)

and

u = w = 0 on z = 0. (5.29)

Applications to the

propagation

of gravity waves 367

We seek an asymptotic solution of these equations in the form

~ J2

e"<7«&

r),

~ £

e"^(|,

r),

«=0

for £ -> 0, where # (and correspondingly #„) represents

w and p. Each

function #„ and

(n = 0,1,2,...) is, in turn, regarded as possessing an

appropriate asymptotic representation as r -> 0, A -> 0; this is equiva-

lent to seeking a multiple asymptotic expansion in terms of, for example,

the asymptotic sequence

n = 0,1,

2,...,

for a suitable set of values

of m and some chosen A(s, r). Further, special problems can always be

posed for any choice A = A(e) and r =

r(e);

that is, R = R(e). On phy-

sical grounds, such a procedure could be criticised since s and R are

clearly

independent

parameters; however, some of the mathematical prob-

lems that are generated in this way enable us to obtain some insight into

the structure of these equations and their solutions. We shall comment on

this again later, but we note here that an ab initio choice of R = R(s)

reduces the problem to an expansion in one parameter - say e - only. To

proceed, the method of solution that we follow here is, in its general

outline, that employed for the derivation of the Korteweg-de Vries

equation (as described in Section 3.2.1).

The leading-order equations, as s -> 0, obtained from equations

(5.25M5.27), are

-wo*

= -Pot +

Ozz

;

u^ +

(5.30)

The boundary conditions, from (5.28) and (5.29), yield

*?o;

= -rj

^ on z=\ (5.31)

and

= w

= 0 on z = 0. (5.32)

It is clear that equations (5.30), for r -> 0, possess a solution which

admits a boundary layer, presumably near z = 0 in the light of the no-

slip boundary condition on z = 0; see Q5.5 and Q5.6. (We might expect a

boundary layer to be required also near z— 1, in order to accommodate

the shear stress condition there. However, as we shall see, the problem of

no wind shear does not give rise to a surface boundary layer at the order

of approximation to which we shall be working.) We therefore seek, in

the first instance, a solution of equations (5.30)-(5.32), in the limit r -> 0

but valid away from the boundary layer near z = 0. This first approx-

imation in r is denoted by an additional zero suffix, so we obtain

368 5 Epilogue

"oot = Poof Pooz = 0; "oo* + woo* = 0,

with

Poo = *?oo;

ooz = 0; w

o = -*?ooi

z=l.

This set produces the familiar solution (see Section 3.2.1)

Poo = *7oo; woo = *?oo; ^00 = -^oo£> 0 < z < 1, (5.33)

which satisfies the shear stress condition (w

oz = 0) on z = 1, but which

cannot satisfy the bottom boundary condition (w

= 0 on z = 0).

Solution (5.33), when previously derived for the KdV equation, was

valid for 0 < z < 1; here it is not valid near z = 0, although both /?oo

and w

o (at this order) would appear to be uniformly valid on

[0,1].

fact solution (5.33) satisfies the full equations valid away from the

boundary layer; see Q5.7.

The equations that define the O(e) problem, from equations (5.25)-

(5.29),

are

+ Au

- u

- cu

+ w

£ + wo^oz = -Pit- + r(u

izz

+ u

->%

= -p

+ rw

Ozz

; u

+ w

= 0,

with

Pi + *?oA)z ~m- 2rw

= 0; u

+ w

^ = 0 | ^ ^ _

and

= wi = 0 on z = 0.

This time we start by retaining the terms in r and A (cf. Q5.7), but we use

the solution previously found, which is valid outside the boundary layer;

in particular, we note that

= 0; A)z = 0; w

= -rj

since (u

, rj

) ~ (woo^oo* rj

) to all (algebraic) orders in r, as we

mentioned above. Thus we obtain the equations

+ Ay/o

- u^ -

crj

+ ^ +

*?o*?o$

= -P\$ + K"izz + ffog); (5.34)

+ w

= 0 (5.35)

Applications to the propagation of gravity waves 369

with

=1> (536)

*7or

+ Ar/or -

*7i£

- cms + J

for the problem outside the boundary layer. We obtain directly from

equations (5.35) and (5.36) (cf. equation (3.26))

and then from equation (5.34)

•Wlz

so that

I rr^yi _1_ ft! I -f ft T T' A Y\ (^ 'X'l\

where /

is an arbitrary function of integration. Finally, the kinematic

condition on z = 1, in (5.36), yields

*?0r + A^or

^lf ~

7oi

3 ^7o^ +

4rr}

, (5.38)

which is to be compared with our conventional KdV equation (3.28):

2*7or +

3*70*70*

+ 3

*?o$g

= 0.

It is left as a simple exercise to confirm that the surface shear stress

condition (in (5.36)) is automatically satisfied since, away from z = 0,

\zz + yog = 0 (to within exponentially small terms as r -> 0); see Q5.8.

The final stage of this calculation involves the construction of the

solution in the boundary layer and hence, via matching, the determina-

tion of the function/

(£,

T; A, r). Once this is done we may return to

our KdV-type equation, (5.38), and consider the size and role of the

370 5

Epilogue

various

new

terms that have appeared.

The

boundary layer,

as is

evident

from equations (5.30),

is in the

region defined

by z =

O(r

1/2

r -» 0, and

then

O(r

1/2

) (from

the

equation

mass conservation

(5.30)).

Thus

introduce

new

variables

= r

Z, w

= r

x/1

& r, T, Z; r)

(5.39)

and, correspondingly,

= U

fo r, T, Z;

r),

= P

& ^ T, Z; r);

of course,

unchanged since

it is not a

function

Equations (5.30)

and (5.32) therefore become

UQS

-P

^ozz;

Poz = 0; U^ +W

= 0

(5.40)

with

= W

= 0 on Z = 0.

see

immediately that

Z > 0,

in order

match

to the

solution

(which merely restates

the uni-

form validity that

have previously noted).

The

equation

for U

then

becomes

with

(5.41)

= 0 on Z =

-> ^

this latter condition ensuring that

C/Q

and

) match.

The problem posed

(5.41)

conveniently reformulated

writing

and f = -f

to give

with

= -?|

onZ = 0; ^^OasZ^ oo.

When we set

& r, T) =

(-f,

r, r) = -

Applications

the propagation of gravity waves

371

the solution (following Duhamel's method, Q5.9) can

written

= -==

((

- f^,

T) exp(-/)

dy,

(5.42)

*\y

--j=f

TH>G

+ ^,r,T)exp(-/)

Ay.

(5.43)

So that

we can

match,

require

the

solution

for W

which, from

equations (5.40)

and

(5.43) becomes

s ^,T, T)exp(-y

)dy ! dZ, (5.44)

satisfying

= 0 on Z =

The

matching

then between (5.44)

Z -> oo,

and

+ f^!

(5.45)

z -> 0; in

particular, written

boundary-layer variables,

z =

x/2

and w

l/2

(5.45) becomes (from (5.33)

and

(5.37))

so matching

(5.44),

as Z ->

00, requires

-J^/o

=^f

exp(-/) dj

dZ.

(5.46)

(Notice that the first term,

—Zrj

automatically matches, confirming the

uniform validity of the solution w

.) The appearance

ofs in

the definition

/o,

through (5.46),

is not

consistent with

our

formulation (since

have already expanded

terms

). This

simply telling

that

precise balance

terms will require

choice

r =

r(e),

and

then

the

cal-

culation repeated with this choice

place;

shall write more

this

shortly.

It is

left

as an

exercise (Q5.10)

demonstrate that, from

equation (5.46), we may write

372

5 Epilogue

Thus,

finally, we have a KdV-type equation which incorporates the

dominant effects of (laminar) viscosity, provided r -> 0 (that is, if the

Reynolds number is large enough); our equation is, from (5.38),

(5.48)

Here, we have retained only the dominant terms associated with

(-> 0)

and r(-> 0); clearly the term 4rrj

^ (in equation (5.38)) is much smaller,

as r -> 0, than that associated with v^/

(although the term r]

^ will

figure in a later calculation). A number of different and important choices

can be made that describe diverse problems, each leading to an appro-

priate balance of terms; we shall return to equation (5.48) in the next

section, but let us here examine the problem we first posed: the slow

modulation of the solitary wave.

The solitary wave, in the absence of any modulation, is a steady solu-

tion of the Korteweg-de Vries equation (that is,

(^)

only), so

= 0,

with the solution

2 '

However, we now incorporate a slow modulation of this solution, on the

scale T, by virtue of the weak viscous contribution. Thus we choose

A =

<s/r/e,

and hence obtain

—2cT}

+ -

with A -> 0 and where

= A<

. (5-49)

yj,

c =

c(T).

(5.50)

The model that we have in mind here is represented in Figure 5.3. The

solitary wave is moving into stationary water and as it does so a (thin)

boundary layer is initiated near the front of the wave. This boundary

layer then grows behind the solitary wave; in the frame at rest relative to

Applications

the propagation

of gravity

waves

373

Solitary wave

Boundary layer

Figure 5.3. Sketch of a solitary wave moving into stationary water with a viscous

boundary layer (on the bottom) growing back from the front of the wave.

the wave, the flow is from right to left and the boundary layer is

stationary in this frame, and growing to the left.

The most direct way to obtain the details of the modulation is to

invoke the condition

770 ^ 0 as |£| -> 00

and to form the integral over all £ of equation (5.49), to give

3 2,1

df'

= A

and then

This identity provides an equation for c(T), which can be obtained by

introducing (5.50) to give

2-7=

•

-00 s