Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves

Подождите немного. Документ загружается.

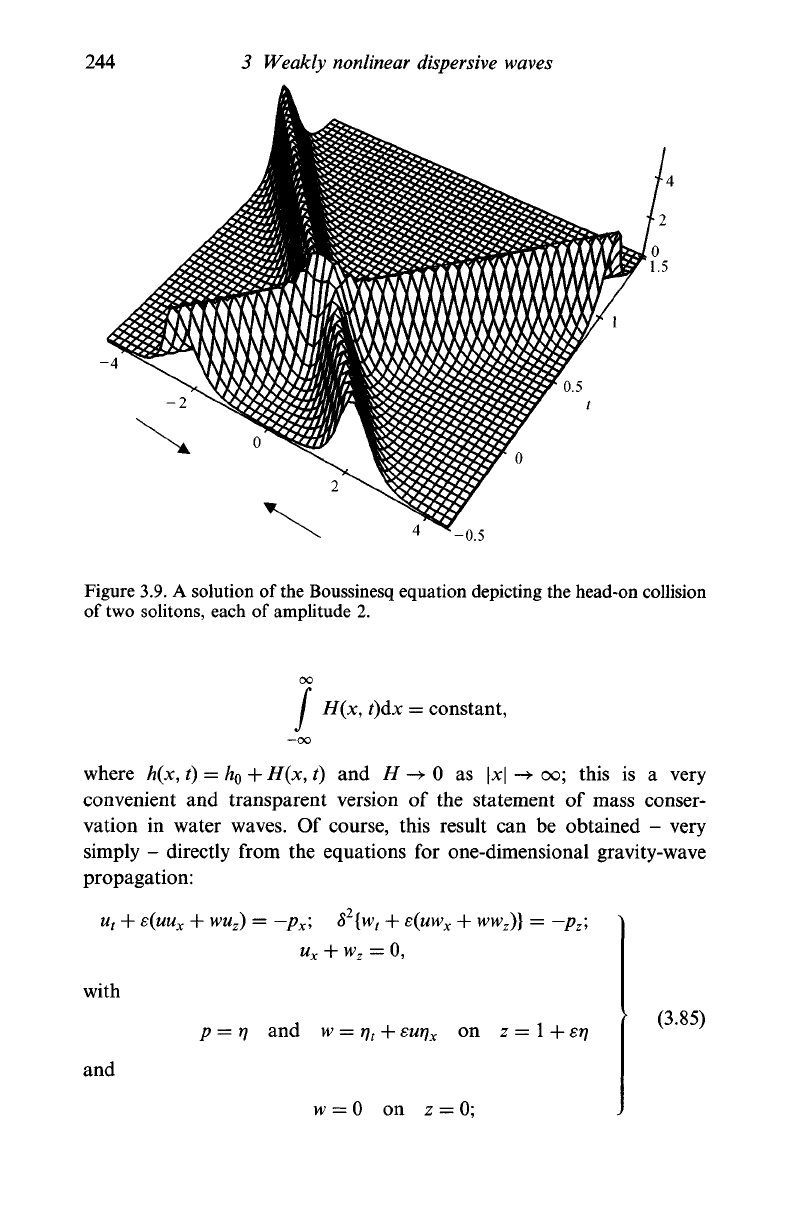
244

3 Weakly nonlinear dispersive waves

Figure 3.9. A solution of

the

Boussinesq equation depicting the head-on collision

of two solitons, each of amplitude 2.

H(JC,

t)dx = constant,

where h(x, i) = h

+ H(x, i) and H -» 0 as |x| ->• oo; this is a very

convenient and transparent version of the statement of mass conser-

vation in water waves. Of course, this result can be obtained - very

simply - directly from the equations for one-dimensional gravity-wave

propagation:

+ e(uu

+ wu

) = -p

+ e(uw

+ ww

)} = -p

with

and

+ w

= 0,

p =

and w =

+ swq

on z =

srj

—

0 on z = 0;

(3.85)

Completely integrable equations

245

see equations (3.9). Thus, employing

the

technique

differentiation

under

the

integral sign,

obtain

•-(

udz\=O

(3.86)

from which

we get

rj(x,

i)dx =

constant. (3.87)

—oo

Similarly,

for

energy

(see

Section

1.2.5), we

obtain directly

l\ I

|^+^^

+ ^|dz}=0 (3.88)

from equations (3.85);

cf.

equation (1.47). (The derivation

this result

left

as an

exercise (Q3.33), although

all the

essential details

are

described

in Section

1.2.5.) The

resulting conserved energy

in the

motion

therefore

l+er)

c I

W + /

+ 8

)dz\dx = constant,

(3.89)

J I

-oo

I 0 J

where decay conditions

infinity have again been invoked. Generally,

expressions

the form

= 0,

(3.90)

where

T(x, t) (the

density)

and X(x, t)

{thzflux)

do not

normally contain

derivatives with respect

to t, are

called conservation laws.

both

T and

are

integrable over

all x, so

that

246

Weakly nonlinear

dispersive

waves

X ->

\x\

oo,

where

is a

constant, we obtain

—

/ Tdx =

or /

T(x,t)dx = constant: (3.91)

the integral

T(x, i) over

all x is a

conserved quantity (often called

constant

the motion, especially when

t is

interpreted

as a

time-like

variable). We have

so far

written down the conservation laws

for

mass

(3.86) and for energy (3.88), as they apply to our one-dimensional water-

wave problem.

It is no

surprise that there

is a

third conservation law,

namely the one that describes the conservation of momentum. There has

been no need to express this in the form (3.90) in our earlier work, but we

will now show how

can be obtained very simply from equations (3.85).

(Ideas that are closely related

to all

three conservation laws have been

developed

the discussion

the jump conditions

Section 2.7.)

Referring to equations (3.85), we see that the first added to eu times the

third yields

2euu

e(uw)

= 0,

and

2euu

) dz

(

t x

) []l

The boundary conditions that describe w then give

2euu

) dz

(rj

) =

where u

is u(x, /, z) evaluated on the surface,

z =

srj.

Again, applica-

tion the method

differentiating under the integral sign produces

+p)dz-^eri

(3.92)

where we have used the surface boundary condition for p (where

p =

rj).

Equation (3.92)

the conservation law

for

momentum which, with

undisturbed background state

place, gives

Completely integrable equations 247

oo /

l+erj

udz\dx = constant, (3.93)

-oo \ 0

the conserved momentum in the motion. Thus, as we must expect, the

passage of the gravity wave (within the confines of our model), conserves

the three fundamental properties of motion: mass, momentum and

energy. The question that we now address is how these conservation

laws - and associated conserved quantities - manifest themselves in our

various KdV-type equations.

We begin this discussion with the KdV equation

itself;

the leading-

order contribution (r/

) to the representation of the surface wave satisfies

equation (3.28):

2*?OT

3770*701

+ 3

*?ot&

= 0

when written in the form of a conservation law. With the assumption that

the wave decays at infinity, so that rj

-> 0 as |£| ->• oo (which is

equivalent to \x\ -> oo for any t), we have

d£ = constant; (3.94)

this is the conservation of mass, equation (3.87). Another conserved

quantity is obtained by multiplying the KdV equation by rj

, to give

(

1/ i

orio

= 0>

a (

a£

r °

= constant. (3.95)

It is clear that the two constants of the motion, (3.94) and (3.95), are

general properties of all solutions of the KdV equations which decay

rapidly enough at infinity. (This also means that, for example, periodic

solutions do not satisfy these particular integral constraints, although an

248 3 Weakly

nonlinear dispersive waves

analogous set of results can be obtained if the integral is taken over just

one period.) The second result, (3.95), should - we must surmise - corre-

spond to the conservation of momentum, equation (3.93). Now from

Section 3.2.1 we find that

f /I 1 i\ 1 2]

u ~ u

+ el

r)i

+ I - - -z Jrj

- -rj

\; u

= rj

z Jrj

(where the KdV equation has been used to eliminate the term

u{)

which is correct at O(£). The first two terms in this integral appear in the

conservation of

mass,

and consequently we must have

= constant,

which recovers (3.95). (The confirmation that the integral of

alone is

itself a constant follows directly from the equation for rj

{

obtained in

Q3.4.)

We have obtained two conserved densities for our KdV equation, rj

and rjl, which correspond to the conservation of mass and momentum,

respectively. We can anticipate that the equation possesses a third

conserved density, which is associated with the energy of the motion.

To see that this is indeed the case, we construct

3rjl

x (KdV) minus

(2^/3) x (a/ag)(KdV) to give

*?o##)

= 0

Completely integrable equations 249

which can be written as

\a/9

42 o2

2 1

v° ~

3 ^°v

r/0

mri

^ ~

* ~

^°^

This is in the form of a conservation law, so we obtain a third conserved

quantity

/ ('nl - ^

*7o$

)

£ = constant, (3.96)

—oo

which is indeed directly related to the total energy given in (3.89) (see

Q3.34).

(In the context of

the

KdV equation treated in isolation, it would

seem reasonable to regard (3.95) as a statement of energy conservation,

since the integrand is a square (that is, proportional to (amplitude)

However, as we have seen, when the appropriate physical interpretation

is adopted, it is (3.96) which corresponds to the conservation of energy.)

The existence of these three conservation laws is to be expected since

our underlying water-wave equations exhibit this same property (where

only conservative forces are involved). However, there is now a real

surprise: the KdV equation possesses an

infinite

number of conservation

laws.

In the early stages of the study of the KdV equation (Miura,

Gardner & Kruskal, 1968), eight further conservation laws were written

down explicitly (having been obtained by extraordinary perseverance);

for example, the next two conserved densities are

—

and

see

Q3.35.

The existence of an infinite set of conservation laws (which will

not be proved here) relates directly to the important idea that the KdV

equation, and other 'soliton' equations, each constitute a completely

integrable Hamiltonian

system',

equivalently, this is to say that the KdV

equation can be written as a Hamiltonian flow. This aspect of soliton

theory is quite beyond the scope of a text that is centred on water-

wave theory, but much has been written on these matters; see the section

on Further Reading at the end of this chapter.

Finally, we briefly indicate the form of some of the conservation laws

that are associated with the standard KdV-type equations. We shall use

250 3 Weakly

nonlinear dispersive waves

here the simplest -

might say normalised - versions of

these

equations

that were introduced in Section

3.3.

First we consider the concentric KdV

equation, (3.64):

+ Y

6uU

x +

xxx

= 0.

It is clear that, for the first two terms,

X12

is an integrating factor; thus we

multiply by t

l/2

to give

x/2

a conserved density. This describes the geometrical decay that is

required to maintain the conservation of mass (cf. equation (3.31)).

Similarly, if

multiply by 2tu, then we obtain

so that another conserved density is tu

; further conserved densities are

discussed in Q3.39.

The Boussinesq equation, (3.43), is

Htt -

xx + 3(// )xx - Hxxxx = 0

which, for our current purpose, is most conveniently written as the pair of

equations

= -U

, U

+ H

- 3(H\ +

xxx

= 0;

cf. equation (3.38). The second equation here is obtained after one inte-

gration in X, coupled with the assumption of decay conditions as

\X\ -^ oo. We now obtain directly

f H

dX = -[£/£„; j U,dX = -[H -

+ H

]«

|OO

•oo

and so

oo oo

/ HdX = constant and /

dX = constant. (3.97)

—00 —OO

The first of these is the conservation of mass and the second is the con-

servation of momentum, an identification which becomes clearer if we

revert to the original x, where

Completely

integrable

equations 251

X = x + e I rjdx

—oo

(see Section 3.2.5), so that

U(\ +

erj)

dx = constant;

cf. equation (3.93). A few other conserved densities are given in Q3.40.

Our third and final example is the two-dimensional KdV equation

which is written here as

- 6uu

+ u

xxx

+ 3v

= 0, u

— v

see equation (3.61) and Section 3.2.2. No longer do we have the classical

form of a (two-dimensional) conservation law: u is a function of three

variables here. This complication produces a development that is less

straightforward. When we integrate the second equation with respect to

and impose decay conditions at infinity, we obtain

—

/ udx] =0 so /

udx=f(t).

However, this is true for all y; let us evaluate the integral for any y that is

far-removed from any wave interaction in, say, the N-soliton solution.

(The 7V-soliton solution of the 2D KdV equation describes the interaction

of waves that asymptote to plane oblique solitary waves at infinity; see

Section 3.3.2 and Q3.19.) In this situation, the function f{i) is a constant;

consequently we obtain

udx = constant, (3.98)

at least for this class of solutions. A similar argument yields the result

vdy = constant; (3.99)

—oo

these two conserved quantities are analogous to the pair (3.97) that we

derived for the Boussinesq equation. To proceed, the integral in x of the

first equation of this pair yields

252 3

Weakly nonlinear dispersive waves

\ / OO \

J^-l

/ vdx\ =0

and so, making use of (3.98) and the same argument as above, we also

have

vdx = constant. (3.100)

The obvious interpretation of equations (3.99) and (3.100) is that

momentum is conserved in both the y- and x- directions; other conser-

vation laws are even less straightforward to obtain and to interpret.

As an intriguing postscript, we mention the equations for shallow

water (obtained in Section 2.6). Following the choices we made there

(of setting s = 1 and writing

srj(x,

t) = h(x, t)), these equations are

+ uu

+ wu

+ h

= 0\ u

+ w

= 0, ^

with 1 (3.101)

w = h

+ uh

on z = h and w = 0 on z = 0. J

We have seen that our water-wave equations, (3.85), admit just the three

physical conservation laws (of mass, momentum and energy). On the

other hand, all our KdV-type equations - that is, completely integrable

equations - possess an infinity of conservation laws. The question we

pose is: how many conservation laws does the set (3.101) possess? The

obvious answer, surely, is just three; let us investigate further.

First, the now very familiar procedure of forming

yields the conservation of mass

h(x,

dx = constant, (3.102)

provided decay conditions obtain. Next, the second equation in (3.101) is

multiplied by u and added to the first to give

+ 2uu

+ (uw)

+ h

= 0,

Completely integrable equations 253

so (cf. equation (3.92)) we obtain

from which we obtain the conservation of momentum

oo /

f f \

/ I / udz \dx = constant. (3.103)

J \ J I

-oo

\0 /

Finally, multiply the first equation by u to produce

and then substitute from the second equation for w

and for u

since h = h(x, i) only. Consequently the integration in z, coupled with

differentiation under the integral sign, yields

oo /

/ /» \

+ /

dz \dx = constant,

J I

\ /

(3.104)

the conserved energy. These three conserved quantities, (3.102), (3.103)

and (3.104), are to be compared with those derived earlier ((3.87), (3.93)

and (3.89)). No surprises here: we have derived the expected conservation

laws for mass, momentum and energy.

We now explore an extension of this process by multiplying the first

equation of (3.101) by u

(and follow the development described by

Benney (1974) and Miura (1974)), to give

3 /I A . 3 /I A . 2 ,2.

wu u

+ u h

= 0;