Johnson R.S. A Modern Introduction to the Mathematical Theory of Water Waves

Подождите немного. Документ загружается.

194 2 Some

classical

problems in water-wave theory

Q2.47 A

circular

shoal. In cylindrical geometry, suppose that the depth

varies so that R

(R) = fiR, where p is a positive constant; see

equation (2.104). Obtain the equation for the rays that approach

from infinity, and describe their behaviour.

Q2.48 A circular

island.

See Q2.47; the depth now varies so that

(R) - /z

= pR

/(R -

RQ),

where fi and R

are positive

constants. Find the equation for the rays and describe their

behaviour as R -> R$ (which is the shoreline).

Q2.49 Ship

waves:

the

wedge

angle.

Describe the behaviour of the angle

of the wedge inside which the dominant ship-wave pattern is

observed as the depth is decreased. (You should consider only

constant speed, straight-line motion.) What is the wedge angle if

= 3c

/41

Q2.50 Ship waves: method of stationary phase. Use Kelvin's method

of stationary phase to show that the dominant asymptotic

behaviour of

/8r

-> oo, is

i ** /i A

S8V28

ASm

8rJ'

Q2.51 Influence points I. A simple geometrical construction enables us

to show that there are just two influence points. Consider the

motion of a point (ship) moving at constant speed in a straight

line;

the ship is at P, and W is any point behind the ship and off

the ship's path. Draw PW, the mid-point of PW at M and the

circle with diameter MW; identify the points (where they exist)

where this circle intersects the path of the ship. Hence deduce

that, at most, only two influence points exist.

Q2.52 Influence points II. Reconstruct the argument used in Q2.51 by an

algebraic method. (For example, show that there are, at most,

only two instants in time before t = 0 at which disturbances

could have been initiated and which contribute to any given

point W). Repeat this calculation for a ship moving on a circular

course at constant speed.

Exercises 195

Q2.53 Ship on a

circular

path. A ship is moving on a circular path, of

radius R

, at a constant speed U. Find the parametric represen-

tation of the curves that describe the dominant wave pattern,

equivalent to equations (2.123). [You may also show how equa-

tions (2.123) are recovered from your equations derived here.]

Q2.54 Ship

waves:

capillary-wave

limit.

Repeat the analysis described in

Section 2.4.2, but now take the dispersion relation for £2 to be

that which describes capillary waves in the absence of gravity

waves (and approximated for long waves). Show that

2tan0tan

0 -

tan0 - tan0 = 0,

and deduce that solutions exist for all

</>

(and so the dominant

waves are no longer confined to a wedge-shaped region).

Q2.55 Simple waves: wave-maker problem. Use the method of

characteristics (Section 2.6.1) to solve the problem of

flow in x > 0, over constant depth, given

h(0,

t) = H(t) for

t > 0 with

w(x,

0) = 0 and h(x, 0) = h

= constant. What is the

corresponding solution if

w(0,

i) = U(t), t > 0, is given?

Q2.56 Simple

waves:

piston

problem.

See Q2.55; repeat this calculation

but now in x > X(t), t > 0; that is, the 'end wall' is moved

according to x = X(t). The water in x > 0 is of constant depth

(/z

), and it is stationary, at t = 0.

[If X\t) < 0, then we generate an expansion fan.]

Q2.57 Simple

waves with

shear

structure.

Use the governing equations

discussed in Section 2.8, but for constant depth b(x) = 0, and

show that we may seek a solution in the form

H(g),

= U&

z),

w = W(l z) g,

for suitable functions H, U

and W, where £ = x

—

and c = c(H). Further, simplify the problem by writing

U = U(H, z) and W = H

W(H,

z);

show that

(U-c)

and that

2 =

(the Burns condition)

196 2 Some

classical problems

water-wave

theory

with I(H, l+H) = l, I(H, 0) = 0, where

I(H,z)=f

(U-c)

(The complete formulation of this problem requires the 'initial'

condition: I(H, z) given at some H; c(H) also must be known,

which is determined from the Burns condition, with either

U - c> 0 or U - c < 0.)

Finally, rewrite this problem in terms of the similarity variable

Z = z/(l + H), so that now / = I(H, Z). Confirm that the choice

= kZ and c'\/\ + H

—

=F3/2

recovers the simple-wave solution

(in the absence of shear) described in Section

2.6.1.

[More information about this problem can be found in

Freeman (1972) and Blythe, Kazakia & Varley (1972); the

Burns condition is described in Burns (1953) and in Thompson

(1949).

We shall provide a discussion involving some properties

of the Burns condition in Chapter 3.]

Q2.58 Nonlinear wave run-up. See Section 2.8; reduce the equation for

t(%,

rj)

to the cylindrical wave equation in T(£ +

rj,

- £) (cf.

Section 2.6.2), and find expressions for w, c, t and x in terms of

T. Hence use the method of separation of variables to find a

solution for T which is bounded at the shoreline. Use your

results to find: (a) the maximum run-up; (b) the behaviour of

the solution far from the shoreline (cf. Section 2.2).

Q2.59 Wave breaking. See Q2.58; the condition for the breaking of the

wave corresponds to where the Jacobian in the hodograph trans-

formation is first zero. Use the results obtained in Q2.58 to show

that breaking first occurs at the shoreline (as we would expect).

[This problem requires the introduction of some identities

involving the Bessel functions J

, J

and J

; a description of

this problem is to be found in Whitham (1979) and Mei (1989).]

Q2.60

Hydraulic

jump and

bore.

Extend the analysis of Section 2.7 for

the case of the hydraulic jump (U = 0), and find the speed of the

flow behind the jump (w

) and verify that u

< u~ if F > 1. In

this case, show that the Froude number for the flow behind the

jump is less than unity.

Use the results obtained here, and in Section 2.7, to describe

the characteristics of the flow associated with a bore which

moves at a speed U into stationary water.

Exercises 197

Q2.61

Reflection

of a bore from a wall Stationary water of depth h

—

is in x < 0, and there is a vertical wall at x = 0. A bore moving at

a constant speed U approaches the wall from

—oo

and is reflected

by it and returns to —

oo.

Find expressions for the speed of the

returning bore and the depth of water behind it.

[The solution of

this

problem reduces to the solution of

cubic

equation, a problem which need not be pursued.]

Q2.62

Circular

hydraulic jump. It is readily observed that water flowing

from a tap into a sink almost always spreads out in a thin, fast-

moving layer over the surface of the sink. Furthermore, this layer

is often approximately circular in shape being terminated by a

narrow region (a jump) where the depth and speed change dra-

matically; thereafter the water makes its way down the plughole.

Consider the problem of

the

circular hydraulic jump and, from

equations (2.2) without the effects of surface tension and without

any variation in 0, follow the methods of Section 2.7 to find the

jump conditions across the circular hydraulic jump.

[Incorporate the long-wave assumption, exactly as in Section

2.7;

a discussion of this problem, with the inclusion of many

realistic physical properties, will be found in Watson (1964).]

Q2.63

Modelling the highest

wave.

Stokes' highest wave can be modelled

by satisfying some appropriate conditions, but not all of them.

The simplest model is obtained by writing

rj = ae-

and then satisfying the conditions that prescribe

rj(O)

and ^'(O),

together with equation (2.166). What is the value of c in this

case?

An improvement is to write

to impose the same conditions as above and, in addition, to

ensure that

3V = (c

- \)M

is satisfied. What now is the value of ct

[The value of c for the highest wave is, based on numerical

evidence, about

1.286;

see Longuet-Higgins & Fenton (1974) for

more details, where it is shown that a wave exists for which

c»

1.294!]

198

Some classical problems

water-wave theory

Q2.64

The

sech

solitary wave. Verify,

or by

direct integration show,

thatthat

solution

equation (2.173), where

f =

—

ex. Confirm that

the behaviour

this solution,

|f |

oo, satisfies

the

condition

(2.166).

Explain

the

connection between

the two

expressions

for

: (2.13)

and

(2.166).

Q2.65 Jacobian elliptic functions. Define

the

integral

d<9

-msin

where m(0<ra<l)isa parameter (called

the

modulus). Then

we write

sn u

sin 0, en u

cos

</>,

the Jacobian elliptic functions; these

are

sometimes written

sn(w|m), cn(w|m). Show that

(a) sn

= 1;

(b) en u

cos u

if m = 0;

en u

sech

if m = 1;

(c)

—

(enw)

— snwdnw where

dnw = y/l

—

msin

and

find

the corresponding results

for the

derivatives

sn u

and

Q2.66 Complete elliptic integral. Define

the

integral

7T/2

K(m)=

jj Vl-mshr0

the complete elliptic integral of the first kind. Deduce that the

period of the elliptic functions sn and en is 4K(m), 0 < m < 1.

Show that

(a) K(0) =

7t/2;

(b) K(m) =

-F(-,-;

1; m), where F(a,b;c;z) is the hyper-

geometric function;

m)}

as m -> 1".

[Hint: in (c) write

= (1 - V^sin0 + ^/msin0)d6.]

Exercises 199

Q2.67

Cnoidal-wave

solution. Verify that

where f = £

—

cz, is a solution of equation (2.173) for suitable

relations between the constants a, b, a and m\ the phase shift, f

is an arbitrary constant.

[For this solution to exist, the cubic, F(f), in Section 2.9.1 has

three real, distinct zeros; indeed, it is convenient to write

where/;, / = 1, 2, 3, are the three roots.]

Q2.68 Circulation associated with a solitary wave. Show that

by evaluating (a) along the bottom streamline; (b) along the

surface streamline (and Stokes' theorem may be invoked).

Q2.69 Integral identities for the

sech

profile.

Examine the three integral

identities, relating T, V, /, C and M (discussed in Section 2.9.2),

when the solitary wave is approximated by the sech

profile of

small amplitude; that is,

is written as st], e -> 0 and

oc sech

(see Section 2.9.1).

Q2.70 Variational principle for water

waves.

Show that the equations for

gravity waves on stationary water over a rigid impermeable

surface (Q1.38) are obtained from the variational principle

Ldxdt =

where the Lagrangian is

i(x,y,t)

The region

Z>,

assumed to contain fluid, is arbitrary; the variations

of 0 and

are zero on the boundaries of

(The nondimensional

parameters, e and 8, are not included in this formulation.)

[These ideas are developed in Luke (1967) and Whitham (1965,

1974).]

Weakly nonlinear dispersive waves

The old order changeth, yielding place to new

The Passing of Arthur

In Chapter 2 we presented some classical ideas in the theory of water

waves. One particular concept that we introduced was the phenomenon

balance between nonlinearity and dispersion, leading to the existence

of the solitary wave, for example. Further, under suitable assumptions,

this wave can be approximated by the sech

function, which is an exact

solution of the Korteweg-de Vries (KdV) equation; see Section

2.9.1.

shall now use this result as the starting point for a discussion of the

equations, and of the properties of corresponding solutions, that arise

when we invoke the assumptions of small amplitude and long wave-

length. In the modern theories of nonlinear wave propagation - and

certainly not restricted only to water waves - this has proved to be an

exceptionally fruitful area of study.

The results that have been obtained, and the mathematical techniques

that have been developed, have led to altogether novel, important and

deep concepts in the theory of wave propagation. Starting from the gen-

eral method of solution for the initial value problem for the KdV equa-

tion, a vast arena of equations, solutions and mathematical ideas has

evolved. At the heart of this panoply is the soliton, which has caused

much excitement in the mathematical and physical communities over

the last 30 years or so. It is our intention to describe some of

these

results,

and their relevance to the theory of water waves, where, indeed, they first

arose.

3.1 Introduction

The existence of a steadily propagating nonlinear wave of permanent

shape, such as the solitary wave, probably seems altogether likely. On

the other hand, that somewhat similar objects could exist in pairs (or

200

Introduction

201

Figure 3.1. A sketch of J. Scott Russell's

compound

wave which 'represents the

genesis by a large low column of fluid of a compound or double wave . . . the

greater moving faster and altogether leaving the smaller'.

larger numbers) of different amplitude, interact nonlinearly and yet not

destroy each other - indeed, retain their identities - would seem rather

unlikely. However, precisely this phenomenon does occur for solutions of

the KdV equation, and for the many other so-called completely integrable

equations.

This very special type of interaction was first observed and described

by Russell (1844); the essentials of his plate XLVII are shown in Figure

3.1.

An obvious interpretation of the development represented in this

figure is that an initial profile, which is not an exact solitary-wave solu-

tion, will evolve into two (or perhaps more) waves which move at differ-

ent speeds and tend to individual solitary waves as time increases.

Another observation, itself an extension of what Russell reported, is

shown in Figure 3.2. This time we have an initial profile comprising

two peaks, the taller to the left of the shorter, but both propagating to

the right. The taller is moving faster (since it is locally similar to a solitary

wave),

and so catches up and then interacts with the shorter, and there-

after moves ahead of it. At first sight, the interaction appears to involve

no interaction at all, as would be the case if the two waves satisfied the

linear superposition principle; cf. equation (1.75) et seq. However, a non-

linear event does occur here, and that it is clearly not linear is confirmed

by the fact that the waves are phase-shifted (by the interaction) from the

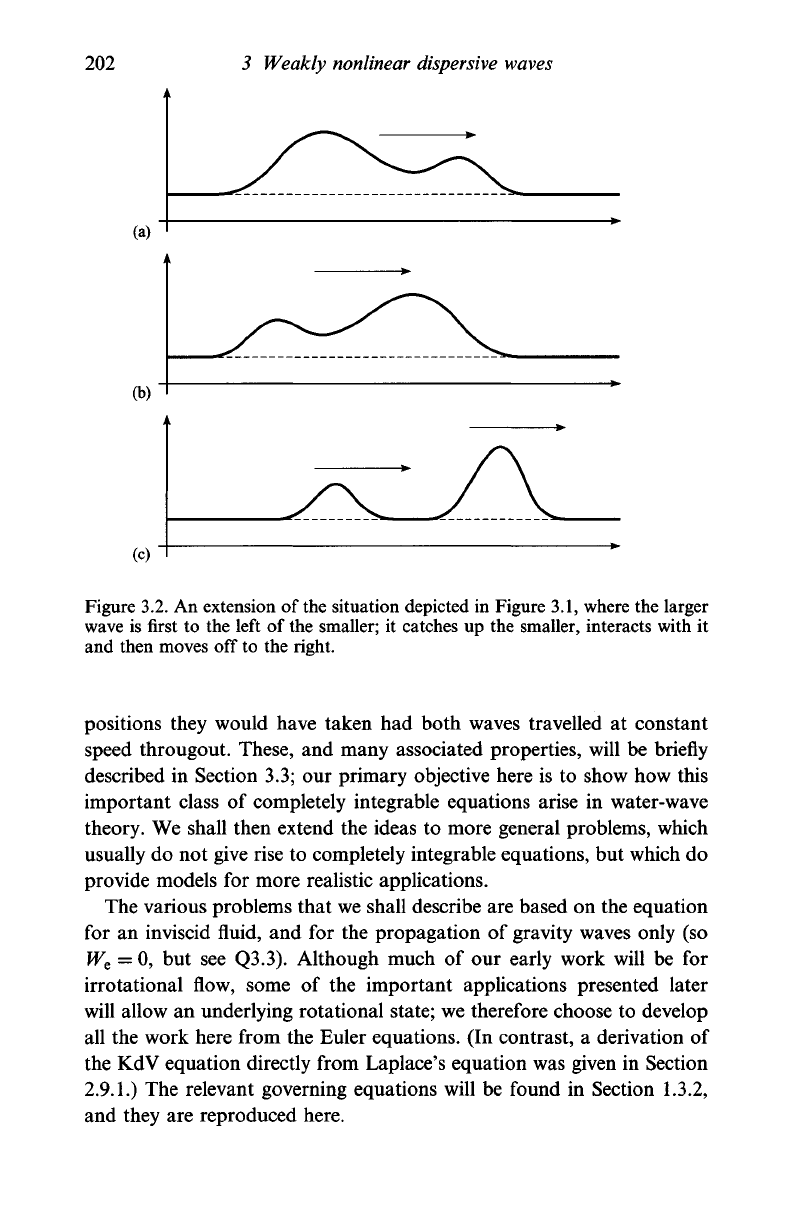
202 3 Weakly nonlinear dispersive waves

(a)

(b)

Figure 3.2. An extension of the situation depicted in Figure 3.1, where the larger

wave is first to the left of the smaller; it catches up the smaller, interacts with it

and then moves off to the right.

positions they would have taken had both waves travelled at constant

speed througout. These, and many associated properties, will be briefly

described in Section 3.3; our primary objective here is to show how this

important class of completely integrable equations arise in water-wave

theory. We shall then extend the ideas to more general problems, which

usually do not give rise to completely integrable equations, but which do

provide models for more realistic applications.

The various problems that we shall describe are based on the equation

for an inviscid fluid, and for the propagation of gravity waves only (so

= 0, but see Q3.3). Although much of our early work will be for

irrotational flow, some of the important applications presented later

will allow an underlying rotational state; we therefore choose to develop

all the work here from the Euler equations. (In contrast, a derivation of

the KdV equation directly from Laplace's equation was given in Section

2.9.1.) The relevant governing equations will be found in Section

1.3.2,

and they are reproduced here.

Introduction

In rectangular Cartesian coordinates we have

where

with

203

DM__ dp Dv _ dp o2

^_ ty

D7~~

ajc' Dt ~ dy' D* ~~ &

D d ( d d d\

—-

h£|

\-V

\-W—

dt \ dx dy dzj

du dv dw

(3.1)

(3.2)

and

. dr\ ( dr\ drj\

p =

and w = \-e\u \-v—I on z—\+er\

dt \ dx dy)

db db _,

W = U

te +

dy °

* = **>*'

Correspondingly, in cylindrical coordinates, we have

(3.3)

(3.4)

_ dp Dv suv _ 1 dp

Dw _ dp

D7~~T

~ar' D7

~r&?' ~Dt

~'dz

where

with

1 3

d v d

I dv dw

(3.5)

(3.6)

and

dri

(

dr\

o.,

and w =

—+

M—+

-— I on

z=l+^

;

dt \ dr r r~ '

db v db

(3.7)

(3.8)

In these equations, and for the following calculations, we consider only

bottom topographies (z = b) which are independent of time.