Jeevanjee N. An Introduction to Tensors and Group Theory for Physicists

Подождите немного. Документ загружается.

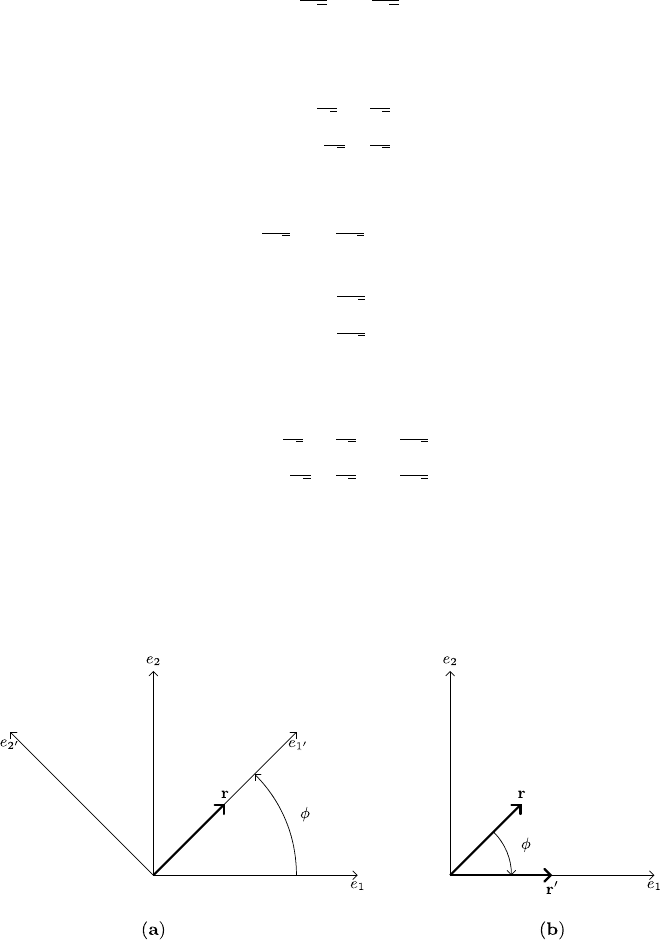
3.3 Active and Passive Transformations 51



≡−

√

You can show (as in Example 3.6) that this leads to an orthogonal change of basis

matrix given by

A =

⎛

⎝

√

−

√

⎞

⎠

(3.41)

which corresponds to rotating our basis counterclockwise by φ = 45°, see

Fig. 3.3(a).

Now consider the vector r =

√

, also depicted in the ﬁgure. In the

standard basis we have

[r]

⎛

⎝

√

⎞

⎠

What does r look like in our new basis? From the ﬁgure we see that r is proportional

to e



, and that is indeed what we ﬁnd; using (3.29)wehave

[r]



=A[r]

⎛

⎝

√

−

√

⎞

⎠

⎛

⎝

√

⎞

⎠



1/2



(3.42)

as expected. Remember that the column vector at the end of (3.42)isexpressedin

the primed basis.

This was the passive interpretation of (3.40); what about the active interpreta-

tion? Taking our matrix A and interpreting it as a linear operator represented in the

standard basis we again have

Fig. 3.3 Illustration of the passive and active interpretations of r



=Ar in two dimensions. In (a)

we have a passive transformation, in which the same vector r is referred to two different bases.

The coordinate representation of r transforms as r



=Ar, though the vector itself does not change.

In (b) we have an active transformation, where there is only one basis and the vector r is itself

transformed by r



=Ar. In the active case the transformation is opposite that of the passive case

52 3Tensors







=A[r]



1/2



(3.43)

except that now the vector (1/2, 0) represents the new vector r



in the same basis B.

This is illustrated in Fig. 3.3(b). As mentioned above, when A is interpreted actively,

it corresponds to a clockwise rotation, opposite to its interpretation as a passive

transformation. 

Exercise 3.11 Verify (3.41)and(3.42).

Example 3.11 Active transformations and rigid body motion

Passive transformations are probably the ones encountered most often in classical

physics, since a change of cartesian coordinates induces a passive transformation.

Active transformations do crop up, though, especially in the case of rigid body

motion. In this scenario, one speciﬁes the orientation of a rigid body by the time-

dependent orthogonal basis transformation A(t) which relates the space frame K



the body frame K(t) (we use here the notation of Example 2.11). As we saw above,

there corresponds to the time-dependent matrix A(t) a time-dependent linear opera-

tor U(t) which satisﬁes U(t)(e



) =e

(t).IfK and K



were coincident at t =0 and

is the position vector of a point p of the rigid body at that time (see Fig. 3.4(a)),

then the position of p at a later time is just r(t) =U(t)r

(see Fig. 3.4(b)), which as

a matrix equation in K



would read



r(t)





=A(t)[r

]



. (3.44)

In more common and less precise notation this would be written

r(t) =A(t)r

In other words, the position of a speciﬁc point on the rigid body at an arbitrary time

t is given by the active transformation corresponding to the matrix A(t). 

Example 3.12 Active and passive transformations and the Schrödinger and Heisen-

berg pictures

The duality between passive and active transformations is also present in quantum

mechanics. In the Schrödinger picture, one considers observables like the momen-

tum or position operator as acting on the state ket while the basis kets remain ﬁxed.

This is the active viewpoint. In the Heisenberg picture, however, one considers the

state ket to be ﬁxed and considers the observables to be time-dependent (recall that

(2.12) is the equation of motion for these operators). Since the operators are time-

dependent, their eigenvectors (which form a basis

) are time-dependent as well, so

this picture is the passive one in which the vectors do not change but the basis does.

For details on why the eigenvectors of Hermitian operators form a basis, at least in the ﬁnite-

dimensional case, see Hoffman and Kunze [10].

3.4 The Tensor Product—Deﬁnition and Properties 53

Fig. 3.4 In (a) we have the coincident body and space frames at t =0, along with the point p of

the rigid body. In (b) we have the rotated rigid body, and the vector r(t) pointing to point p now

has different components in the space frame, given by (3.44)

Just as an equation like (3.40) can be interpreted in both the active and passive sense,

a quantum mechanical equation like

< ˆx(t)> =ψ|



†

ˆxU



|ψ (3.45)



ψ|U

†



ˆx



U|ψ



, (3.46)

where U is the time-evolution operator for time t , can also be interpreted in two

ways: in the active sense of (3.46), in which the U s act on the vectors and change

them into new vectors, and in the passive sense of (3.45), where the U s act on the

operator ˆx by a similarity transformation to turn it into a new operator, ˆx(t).

3.4 The Tensor Product—Deﬁnition and Properties

One of the most basic operations with tensors, again commonplace in physics but

often unacknowledged (or, at best, dealt with in an ad hoc fashion) is that of the ten-

sor product. Before giving the precise deﬁnition, which takes a little getting used to,

we give a rough, heuristic description. Given two ﬁnite-dimensional vector spaces

V and W (over the same set of scalars C), we would like to construct a product vec-

tor space, which we denote V ⊗ W , whose elements are in some sense ‘products’

of vectors v ∈V and w ∈W . We denote these products by v ⊗w. This product, like

54 3Tensors

any respectable product, should be bilinear in the sense that

) ⊗w =v

⊗w +v

⊗w (3.47)

v ⊗(w

) =v ⊗w

+v ⊗w

(3.48)

c(v ⊗w) =(cv) ⊗w =v ⊗(cw), c ∈C. (3.49)

Given these properties, the product of any two arbitrary vectors v and w can then be

expanded in terms of bases {e

}

i=1,...,n

and {f

}

j=1,...,m

for V and W as

v ⊗w =





⊗





⊗f

so {e

⊗f

}, i =1,...,n, j =1,...,m should be a basis for V ⊗W , which would

then have dimension nm. Thus the basis for the product space would be just the

product of the basis vectors, and the dimension of the product space would be just

the product of the dimensions.

Now we make this precise. Given two ﬁnite-dimensional vector spaces V and W ,

we deﬁne their tensor product V ⊗W to be the set of all C-valued bilinear functions

on V

∗

×W

∗

. Such functions do form a vector space, as you can easily check. This

deﬁnition may seem unexpected or counterintuitive at ﬁrst, but you will soon see

that this deﬁnition does yield the vector space described above. Also, given two

vectors v ∈ V , w ∈W , we deﬁne their tensor product v ⊗ w to be the element of

V ⊗W deﬁned as follows:

(v ⊗w)(h, g) ≡v(h)w(g) ∀h ∈V

∗

,g∈W

∗

. (3.50)

(Remember that an element of V ⊗ W is a bilinear function on V

∗

×W

∗

, and so

is deﬁned by its action on a pair (h, g) ∈ V

∗

× W

∗

.) The bilinearity of the tensor

product is immediate and you can probably verify it without writing anything down:

just check that both sides of (3.47)–(3.49) are equal when evaluated on any pair

of dual vectors. To prove that {e

⊗ f

}, i = 1,...,n, j = 1,...,m is a basis for

V ⊗W ,let{e

}

i=1,...,n

, {f

}

i=1,...,m

be the corresponding dual bases and consider

an arbitrary T ∈V ⊗W . Using bilinearity,

T(h,g)=h





(3.51)

where T

≡T(e

). If we consider the expression T

⊗f

, then



⊗f













so T

⊗ f

agrees with T on basis vectors, hence on all vectors by bilinear-

ity, so T = T

⊗ f

. Since T was an arbitrary element of V ⊗ W , V ⊗ W =

Span{e

⊗ f

}. Furthermore, the e

⊗ f

are linearly independent as you should

check, so {e

⊗f

}is actually a basis for V ⊗W and V ⊗W thus has dimension mn.

3.5 Tensor Products of V and V

∗

The tensor product has a couple of important properties besides bilinearity. First,

it commutes with taking duals, that is,

(V ⊗W)

∗

⊗W

∗

. (3.52)

Secondly, and more importantly, the tensor product it is associative, i.e. for vector

spaces V

, i =1, 2, 3,

⊗V

) ⊗V

⊗(V

⊗V

). (3.53)

This property allows us to drop the parentheses and write expressions like

⊗···⊗V

without ambiguity. One can think of V

⊗···⊗V

as the set of

C-valued multilinear functions on V

∗

×···×V

∗

These two properties are both plausible, particularly when thought of in terms

of basis vectors, but verifying them rigorously turns out to be slightly tedious. See

Warner [18] for proofs and further details.

Exercise 3.12 If {e

}, {f

} and {g

} are bases for V

, V

and V

, respectively, convince

yourself that {e

⊗f

⊗g

} is a basis for V

⊗V

, and hence that dim V

⊗V

where dim V

. Extend the above to n-fold tensor products.

3.5 Tensor Products of V and V

∗

In the previous section we deﬁned the tensor product for two arbitrary vector spaces

V and W . Often, though, we will be interested in just the iterated tensor product of

a vector space and its dual, i.e. in tensor products of the form

∗

⊗···⊗V

∗

  

r times

⊗V ⊗···⊗V



 

s times

. (3.54)

This space is of particular interest because it is actually identical to T

! In fact, from

the previous section we know that the vector space in (3.54) can be interpreted as

the set of multilinear functions on

V ×···×V



 

r times

×V

∗

×···×V

∗

  

s times

but these functions are exactly T

. Since the space in (3.54) has basis B

⊗···⊗e

⊗ e

⊗···⊗e

}, we can conclude that B

is a basis for T

.In

fact, we claim that if T ∈T

has components T

...i

...j

, then

T =T

...i

...j

⊗···⊗e

⊗e

⊗···⊗e

(3.55)

is the expansion of T in the basis B

. To prove this, we just need to check that

both sides agree when evaluated on an arbitrary set of basis vectors; on the left hand

side we get T(e

,...,e

) =T

,...,i

...j

by deﬁnition, and on the right

56 3Tensors

hand side we have



...k

...l

⊗···⊗e

⊗e

⊗···⊗e



,...,e



...k

...l

)...e





...e





...k

...l

...δ

,...,i

...j

(3.56)

so our claim is true. Thus, for instance, a (2, 0) tensor like the Minkowski met-

ric can be written as η = η

μν

⊗ e

. Conversely, a tensor product like f ⊗ g =

⊗e

∈T

thus has components (f ⊗g)

. Notice that we now have

two ways of thinking about components: either as the values of the tensor on sets

of basis vectors (as in (3.5)) or as the expansion coefﬁcients in the given basis (as

in (3.55)). This duplicity of perspective was pointed out in the case of vectors just

above Exercise 2.10, and it is essential that you be comfortable thinking about com-

ponents in either way.

Exercise 3.13 Compute the dimension of T

Exercise 3.14 Let T

and T

be tensors of type (r

) and (r

), respectively, on a vector

space V . Show that T

⊗T

can be viewed as an (r

) tensor, so that the tensor

product of two tensors is again a tensor, justifying the nomenclature.

One important operation on tensors which we are now in a position to discuss is

that of contraction, which is the generalization of the trace functional to tensors of

arbitrary rank: Given T ∈T

(V ) with expansion

T =T

...i

...j

⊗···⊗e

⊗e

⊗···⊗e

(3.57)

we can deﬁne a contraction of T to be any (r − 1,s − 1) tensor resulting from

feeding e

into one of the arguments, e

into another and then summing over i as

implied by the summation convention. For instance, if we feed e

into the rth slot

and e

into the (r +s)th slot and sum, we get the (r −1,s−1) tensor

T deﬁned as

T(v

,...,v

r−1

,...,f

s−1

) ≡T



,...,v

r−1

,...,f

s−1



You may be suspicious that

T depends on our choice of basis, but Exercise 3.15

shows that contraction is in fact well-deﬁned. Notice that the components of

T are

...i

r−1

...j

s−1

...i

r−1

...j

s−1

Similar contractions can be performed on any two arguments of T provided one ar-

gument eats vectors and the other dual vectors. In terms of components, a contrac-

tion can be taken with respect to any pair of indices provided that one is covariant

and the other contravariant. If we are working on a vector space equipped with a

metric g, then we can use the metric to raise and lower indices and so can contract

on any pair of indices, even if they are both covariant or contravariant. For instance,

we can contract a (2, 0) tensor T with components T

T = T

, which

one can interpret as just the trace of the associated linear operator (or (1, 1) tensor).

3.5 Tensor Products of V and V

∗

For a linear operator or any other rank 2 tensor, this is the only option for contrac-

tion. If we have two linear operators A and B, then their tensor product A ⊗B ∈T

has components

(A ⊗B)

and contracting on the ﬁrst and last index gives a (1, 1) tensor AB whose compo-

nents are

(AB)

You should check that this tensor is just the composition of A and B, as our nota-

tion suggests. What linear operator do we get if we consider the other contraction

Exercise 3.15 Show that if {e

}

i=1,...,n

and {e



}

i=1,...,n

are two arbitrary bases that



,...,v

r−1

,...,f

s−1





,...,v

r−1



,...,f

s−1





so that contraction is well-deﬁned.

Example 3.13 V

∗

⊗V

One of the most important examples of tensor products of the form (3.54)isV

∗

⊗V ,

which as we mentioned is the same as T

, the space of linear operators. How does

this identiﬁcation work, explicitly? Well, given f ⊗ v ∈ V

∗

⊗ V , we can deﬁne a

linear operator by (f ⊗v)(w) ≡f(w)v. More generally, given

⊗e

∈V

∗

⊗V, (3.58)

we can deﬁne a linear operator T by

T(v)=T

(v)e

which is identical to (2.13). This identiﬁcation of V

∗

⊗ V and linear operators is

actually implicit in many quantum mechanical expressions. Let H be a quantum

mechanical Hilbert space and let ψ,φ ∈H so that L(φ) ∈ H

∗

. The tensor product

of L(φ) and ψ , which we would write as L(φ) ⊗ψ, is written in Dirac notation as

|ψφ|. If we are given an orthonormal basis B ={|i}, the expansion (3.58)ofan

arbitrary operator H can be written in Dirac notation as

H =



i,j

|ij |,

an expression which may be familiar from advanced quantum mechanics texts.

particular, the identity operator can be written as

I =



|ii|,

which is referred to as the resolution of the identity with respect to the basis {|i}.

We do not bother here with index positions since most quantum mechanics texts do not employ

Einstein summation convention, preferring instead to explicitly indicate summation.

58 3Tensors

A word about nomenclature: In quantum mechanics and other contexts the tensor

product is often referred to as the direct or outer product. This last term is meant

to distinguish it from the inner product, since both the outer and inner products eat

a dual vector and a vector (strictly speaking the inner product eats 2 vectors, but

remember that with an inner product we may identify vectors and dual vectors) but

the outer product yields a linear operator whereas the inner product yields a scalar.

Exercise 3.16 Interpret e

⊗e

as a linear operator, and convince yourself that its matrix

representation is



⊗e



Recall that E

is one of the elementary basis matrices introduced way back in Example 2.8,

and has a 1 in the j th row and ith column and zeros everywhere else.

3.6 Applications of the Tensor Product in Classical Physics

Example 3.14 Moment of inertia tensor revisited

We took an abstract look at the moment of inertia tensor in Example 3.3;now,

armed with the tensor product, we can examine the moment of inertia tensor more

concretely. Consider a rigid body with a ﬁxed point O, so that it has only rotational

degrees of freedom (O need not necessarily be the center of mass). Let O be the

origin, pick time-dependent body-ﬁxed axes K ={

x(t),

y(t),

z(t)} for R

, and let g

denote the Euclidean metric on R

. Recall that g allows us to deﬁne a map L from

to R

3∗

. Also, let the ith particle in the rigid body have mass m

and position

vector r

with [r

]

= (x

) relative to O, and let r

≡ g(r

, r

). All this is

illustrated in Fig. 3.5.The(2, 0) moment of inertia tensor is then given by

(2,0)





g −L(r

) ⊗L(r

)



(3.59)

while the (1, 1) tensor reads

(1,1)





I −L(r

) ⊗r



. (3.60)

You should check that in components (3.59) reads





−(r

)



Writing a couple of components explicitly yields







=−



(3.61)

3.6 Applications of the Tensor Product in Classical Physics 59

Fig. 3.5 The rigid body with ﬁxed point O and body-ﬁxed axes K ={

z}, along with ith

particle at position r

with mass m

expressions which should be familiar from classical mechanics. So long as the basis

is orthonormal, the components I

of the (1, 1) tensor in (3.60) will be the same

as for the (2, 0) tensor, as remarked earlier. Note that if we had not used body-ﬁxed

axes, the components of r

(and hence the components of I,by(3.61)) would in

general be time-dependent; this is the main reason for using the body-ﬁxed axes in

computation.

Example 3.15 Maxwell stress tensor

In considering the conservation of total momentum (mechanical plus electromag-

netic) in classical electrodynamics one encounters the symmetric rank 2 Maxwell

Stress Tensor, deﬁned in (2, 0) form as

(2,0)

=E ⊗E +B ⊗B −

(E ·E +B ·B)g

where E and B are the dual vector versions of the electric and magnetic ﬁeld vec-

tors. T can be interpreted in the following way: T(v,w) gives the rate at which

momentum in the v-direction ﬂows in the w-direction. In components we have

−

(E ·E +B ·B)δ

which is the expression found in most classical electrodynamics textbooks.

Recall that we have set all physical constants such as c and 

equal to 1.

60 3Tensors

Example 3.16 The electromagnetic ﬁeld tensor

As you has probably seen in discussions of relativistic electrodynamics, the electric

and magnetic ﬁeld vectors are properly viewed as components of a rank 2 antisym-

metric tensor F , the electromagnetic ﬁeld tensor.

To write F in component-free

notation requires machinery outside the scope of this text,

so we settle for its ex-

pression as a matrix in an orthonormal basis, which in (2, 0) form is

(2,0)

⎛

⎜

⎝

0 E

−E

0 −B

−E

0 −B

−E

−B

⎞

⎟

⎠

. (3.62)

The Lorentz force law

dτ

=qF

where p =mv is the 4-momentum of a particle, v is its 4-velocity and q its charge,

can be rewritten without components as

dτ

=qF

(1,1)

(v) (3.63)

which just says that the Minkowski force

dτ

on a particle is given by the action of

the ﬁeld tensor on the particle’s 4-velocity!

3.7 Applications of the Tensor Product in Quantum Physics

In this section we will discuss further applications of the tensor product in quantum

mechanics, in particular the oft-unwritten rule that to add degrees of freedom one

should take the tensor product of the corresponding Hilbert spaces. Before we get

to this, however, we must set up a little more machinery and address an issue that

we have so far swept under the rug. The issue is that when dealing with spatial

degrees of freedom, as opposed to ‘internal’ degrees of freedom like spin, we often

encounter Hilbert spaces like L

([−a,a]) and L

(R) which are most conveniently

described by ‘basis’ vectors which are eigenvectors of either the position operator ˆx

or the momentum operator ˆp. The trouble with these bases is that they are often non-

denumerably inﬁnite (i.e. cannot be indexed by the integers, unlike all the bases we

have worked with so far) and, what is worse, the ‘basis vectors’ do not even belong

In this example and the one above we are actually not dealing with tensors but with tensor ﬁelds,

i.e. tensor-valued functions on space and spacetime. For the discussion here, however, we will

ignore the spatial dependence of the ﬁelds, focusing instead on the tensorial properties.

One needs the exterior derivative, a generalization of the curl, divergence and gradient operators

from vector calculus. See Schutz [15] for a very readable account.