Изучение затухающих колебаний физического маятника
Подождите немного. Документ загружается.

ГОУ ВПО
ДВГУПС
Кафедра “Физика”
Л А Б О Р А Т О Р Н А Я Р А Б О Т А
На тему: “Изучение затухающих колебаний физического маятника ”
21040165 11М 911
Шифр Номер работы Группа
Выполнил
Черных Д. С.
Проверил:
Старший преподаватель
кафедры “Оптические
системы связи”
Бодров Е. А.
Хабаровск 2006 г.

Цель работы:
Определить период колебаний физического маятника. Определить
коэффициент затухания физического маятника.
Приборы и оборудование:
Кронштейн с линейкой, металлический стержень, набор грузов,
секундомер.
Краткая теория:
Колебательным движением называется изменение состояния,
характеризуемого повторяемостью во времени значений физических
величин, характеризующих это состояние
Колебательное движение называется периодическим, если значения
изменяющихся физических величин повторяются через равные промежутки
времени. Простейшее периодическое колебание, при котором физическая
величина изменяется по закону синуса или косинуса называется
гармоническим.
0
0
sin
cos
tAx
tAx
- уравнение собственных свободных колебаний, где
Х – смещение точки от положения равновесия; А – амплитуда колебаний
(величина, равная максимальному смещению колеблющегося тела от
положения равновесия);
0
t
- фаза колебания точки (стоит под
законом косинуса и определяет долю, которую смещение составляет от
максимального);
0
- начальная фаза колебания точки;
- циклическая
частота колебаний (величина, определяемая числом полных колебаний,
совершенных за
2
секунд).
Циклическая частота колебаний численно равна произведению
2
секунд и частоте колебаний (
- величина равная числу полных колебаний
за единицу времени).
После некоторых преобразований закона гармонического
колебательного движения получено, что ускорение и скорость точки
меняются со временем по гармоническому закону с той же самой угловой
частотой
и периодом
2
T
. Максимальное значение скорости равно
Av
0
, а максимальное значение ускорения
Aa
2
0
. Колебания скорости
опережают колебания смещения по фазе на
2
, а колебания ускорения
опережают колебания смещения по фазе на
.
В условиях, когда на тело действует только одна квазиупругая сила,
тело будет совершать свободные незатухающие гармонические колебания с
постоянной амплитудой. В реальных условиях на тело действует со стороны
окружающей среды сила трения, препятствующая его движению. На
преодоление сопротивления среды, трение в опорах, создание волн и т.п.
будет затрачиваться энергия. Вследствие этого механическая энергия
колеблющегося тела будет непрерывно уменьшаться. Учитывая

вышеописанное, формулируем полную энергию материальной точки:
2
22
Am
E
.
Таким образом, полная энергия гармонически колеблющейся точки
есть величина постоянная и пропорциональная квадрату амплитуды
колебаний.
С уменьшением энергии в реальных системах будет уменьшаться
амплитуда, и колебание станет затухающим.
Полная сила, действующая на колеблющуюся точку, будет суммой
квазиупругой силы и силы трения. При малых скоростях движение
сопротивление обычно пропорционально первой степени скорости и
направленно противоположно ей.
Коэффициент затухания
m
r
2
, где
r
- коэффициент трения,
зависящий от окружающей среды. Следовательно, чем больше коэффициент
трения, тем больше коэффициент затухания, тем быстрее амплитуда
затухающих колебаний убывает со временем. Также отметим, что при
наличии трения не только убывает со временем амплитуда колебания, но и
уменьшается угловая частота колебаний
22
0
, где
0
- циклическая
частота собственных колебаний точки при отсутствии трения.
Соответственно период затухающих колебаний равен
22
0
2
T
.
С увеличением трения период возрастает, и при равных значениях
коэффициента затухания и циклической частоты собственных колебаний
точки при отсутствии трения стремится к бесконечности.
При дальнейшем увеличении
, период становится мнимым, а
движение точки апериодическим.
А если сопоставить при
0
значения амплитуд в разные моменты
времени, получим, что амплитуда затухающих колебаний за каждый период
убывает в одно и то же число раз.
Логарифм отношения двух соседних амплитуд носит название
логарифмического декремента затухания
T
Tta
tA
ln
.
Время
, в течение которого амплитуда уменьшается в
e
раз,
называется временем релаксации. За время релаксации система совершает
T
N
e
колебаний,
1
0
1
e
eA
A
N
, тогда
1 T
,
1
, следовательно,
коэффициент затухания есть физическая величина, обратная времени
релаксации. Логарифмический декремент затухания обратно пропорционален
по величине числу колебаний N, совершаемых за время релаксации.
Характеристикой колебательной системы служит величина, называемая
добротностью колебательной системы, которая при малых значениях
логарифмического декремента равна
2
0
Q
.
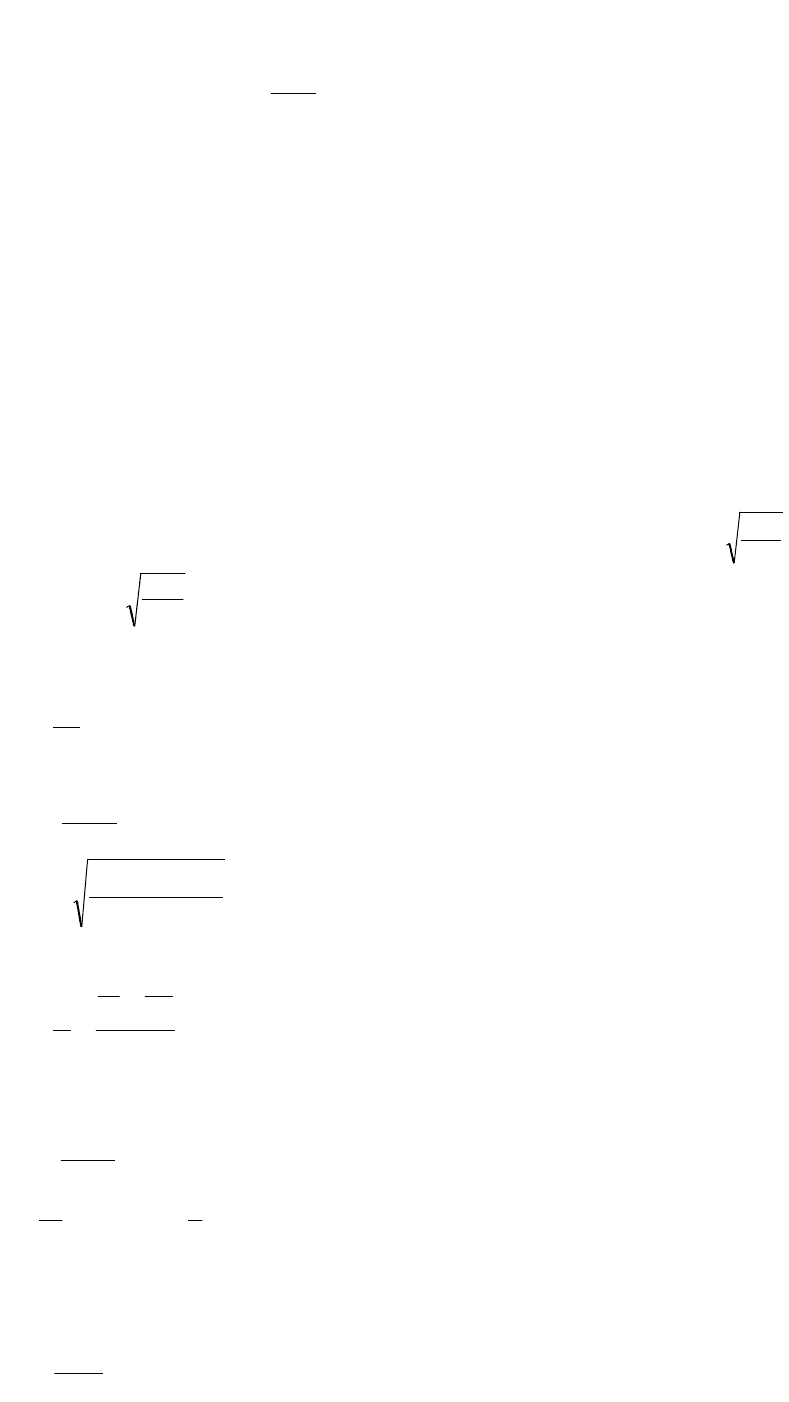
Так как затухания невелики, то
T
принято равным
0
T
. Величину
добротности можно представить через энергетические характеристики
колеблющейся системы
E
E
Q
2
, где E – энергия колебательной системы в
произвольный момент времени t,
E
- убыль этой энергии за промежуток
времени от t до t + T, т.е. за один условный период затухающих колебаний.
Физический маятник – это твердое тело, совершающее под действием
силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса,
не проходящей через центр масс тела. Если физический маятник вывести из
положения равновесия, отклонив его на некоторый угол, то силу тяжести
маятника можно разложить на две составляющие силы: нормальную
составляющую, направленную вдоль оси маятника и уравновешиваемую
силой реакции оси, и тангенциальную составляющую, которая может
считаться квазиупругой и создает возвращающий момент. Преобразовав
некоторые уравнения относящиеся к закону динамики для вращательного
движения получаем: при малых углах отклонения физический маятник
совершает гармонические колебания с циклической частотой
I
mgl
0
и
периодом
mgl
I
T
2
.
Расчетные формулы:
N
t
T
N
n
- период колебаний для каждого опыта в отдельности
n
T
T
n
i
i
ср
1
- среднее значение периода колебаний
1
2
NN
TT
T
ср
- погрешность значения периода колебаний
TTT
ср
- период колебаний с учетом погрешности
T
N
T
n
n
0
ln
1
- коэффициент затухания для каждого опыта в
отдельности
n
n
i
i
ср
1
- среднее значение коэффициента затухания
2222
5
2
12
1
шшшст
lmRmmlmlI
- момент инерции для исследуемого
физического маятника
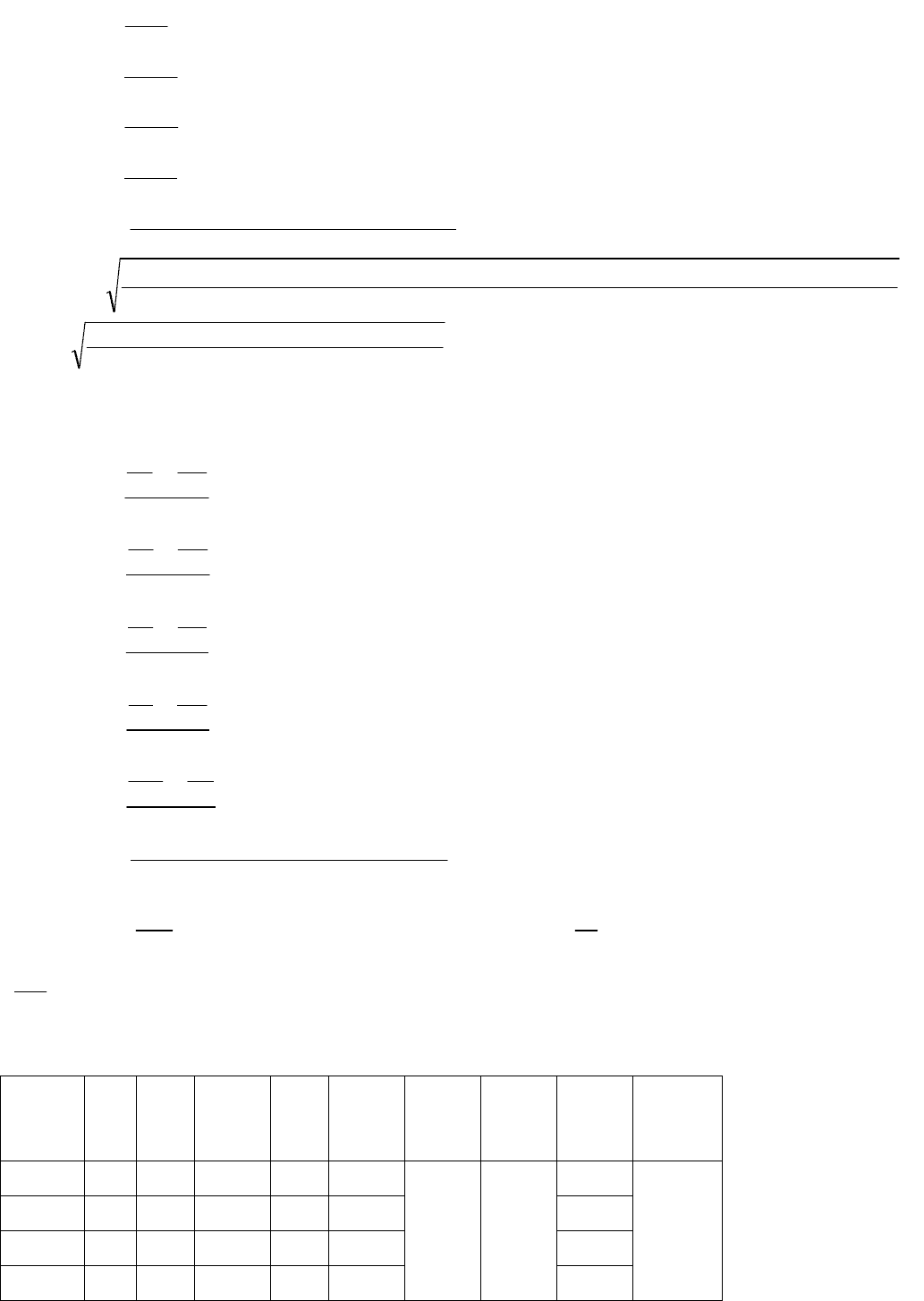
Проведем соответствующие расчеты и измерения:
795,1
20
9,35
1
T
с
785,1
40
4,71
2
T
с
788,1
60
3,107
3
T
с
815,1
80
2,145
4
T
с
793,1
100
3,179
5
T
с
795,1
5
793,1815,1788,1785,1795,1
ср
T
с
005,0
20
000004,00004,0000064,00001,0
95,0
155
793,1795,1815,1795,1788,1795,1785,1795,1795,1795,1
95,0
22222
T
79,1
8,1
005,0795,1
T
T
T
с
01,0
795,1
5,5
8
ln
20
1
1
008,0
785,1
5,4
8
ln
40
1
2
008,0
788,1
5,3
8
ln
60
1
3
008,0
815,1
5,2
8
ln
80
1
4
009,0
793,1
5,1
8
ln
100
1
5
0086,0
5
009,0008,0008,0008,001,0
ср
207,0151,0000024,0042,0014,0
87,02,01025,182,0
5
2
0462,092,02,0
12
1
2
2
322
I
2
м
кг
Систематизируем результаты в виде таблицы:
№ п/п
0
N
N
t
,
с
N
T
,
с
ср
T
,
с
T
,
с
ср
1 8 20 35,9 5,5 1,795
1,795 0,005
0,01
0,0086
2 8 40 71,4 4,5 1,785 0,008
3 8 60 107,3 3,5 1,788 0,008
4 8 80 145,2 2,5 1,815 0,008

5 8 100 179,3 1,5 1,793 0,009
Вывод:
Выполнив данную работу, я при помощи метода прямых и косвенных
измерений определил период колебаний физического маятника с учетом
погрешности, рассчитал его коэффициент затухания, а также вычислил
момент инерции для данного физического маятника.
Из анализа полученных результатов следует, что периоды колебаний
для каждого отдельного опыта (при N=20, 40, 60 и т.д.) отличаются не более
чем на 0,02 секунды, что не очень значительно; значение коэффициента
затухания для каждого опыта в отдельности аналогично периоду почти не
разнится. Среднее значение коэффициента затухания для данной работы, по
моим подсчетам составило 0,0086.
Также я вычислил момент инерции для данного физического маятника,
полученный результат равен 0,207
2
м
кг
.
В качестве оборудования и измерительных приборов мною были
использованы кронштейн с линейкой, металлический стержень, набор грузов,
секундомер.
