Измерение электрического сопротивления мостом Уитстона
Подождите немного. Документ загружается.

Лабораторная работа №63.
ИЗМЕРЕНИЕ ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ МОСТОМ
УИТСТОНА
Цель работы: Изучить мост Уитстона как прибор для измерения сопротивления.
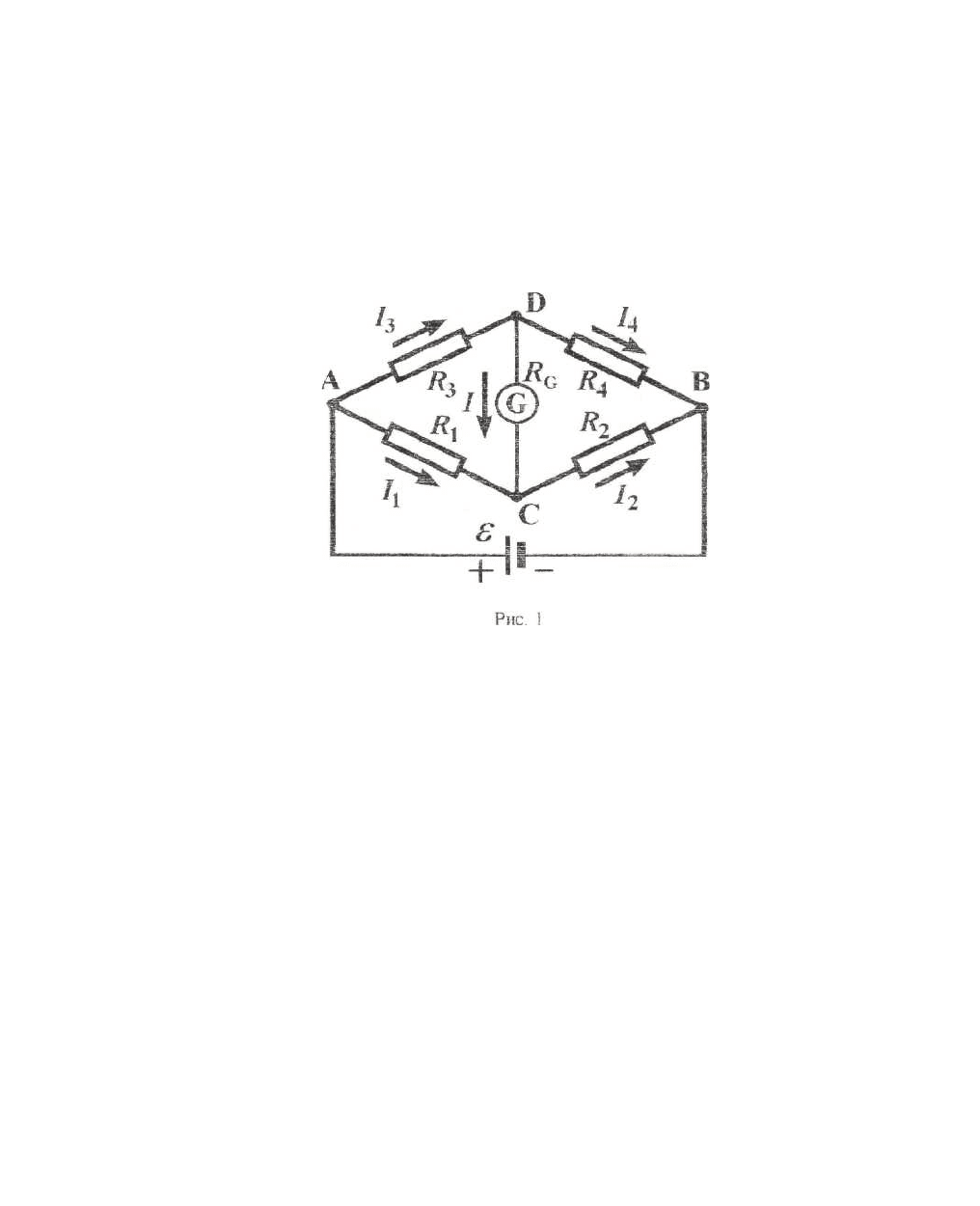
Теория: Мостом Уитстона называется электрическая цепь, состоящая из источника эдс ε,
гальванометра G и четырех резисторов R
1
R
2
, R
3
, R
4
, которые связаны между собой посредством
узлов А, В, С и D, т.е. точек, в которых сходятся не менее трех проводников с током (рис 1)
Однородные участки цепи между соседними узлами, содержащие только резисторы R
1
, R
2
, R
3
и R
4
называются плечами моста. Собственно роль моста выполняет участок CD, по которому в
зависимости от соотношения сопротивлений R
1
, R
2
, R
3
и R
4
электрический ток может протекать во
взаимно противоположных направлениях. Гальванометр служит индикатором равновесия моста, то
есть такого состояния, когда ток через участок CD не течет. Мост Уитстона находит широкое
применение в различных радиотехнических устройствах и в измерительной технике. В частности,
для измерения электрического сопротивления.
Для вывода рабочей формулы воспользуемся правилами Кирхгофа. Сначала на схеме следует
обозначить все токи, текущие по отдельным ветвям цепи, сопротивления, полярности источников и
узлы. Обозначим силу тока через гальванометр с внутренним сопротивлением R
G
буквой I, а в
плечах R
1
, R
2
, R
3
, R
4
соответственно I
1
, I
2
, I
3
, I
4
. Обычно токи, направленные к узлу, считаются
положительными, а токи, выходящие из узла - отрицательными. Согласно первому правилу
Кирхгофа алгебраическая сумма сил токов в узле, равна нулю: Σ
i
I
i
= 0. Применяя его к узлам С и
D, имеем:
I
1
-I
2
+I= 0 (1)
I
3
-I
4
-I= 0 (2)
Согласно второму правилу, в любом замкнутом контуре алгебраическая сумма
произведений сил токов Ii, и значений сопротивлений R
j
, по которым текут эти токи, равна
алгебраической сумме эдс εj в контуре, то есть Σ
j
I
j
R
j
=Σ
j
ε
j
. Для правильного выбора знаков силы
тока и эдс необходимо задаться направлением обхода в каждом контуре, например, по часовой
стрелке. Токи, направления которых совпадают с направлением обхода контура, считаются
положительными (I
3
и I в контуре ADCA). Отрицательными будут токи, текущие против
направления обхода (I
2
и I в контуре DBCD). Эдс считаются положительными, если они
повышают потенциал в направлении обхода, и отрицательными, если они понижают его. В
упомянутых контурах источников эдс нет. С учетом выше изложенного получается:
Для контура ADCA: I
3
R
3
+IR
G
-I
1
R
1
= 0 (3)
Для контура DBCD: I
4
R
4
+I
2
R
2
-IR
G
= 0 (4)
При равновесии моста I= 0 . В этом случае, сопротивления R
1
, R
2
, R
3
и R
4
удовлетворяют
соотношению: R
1
/R
2
=R
3
/R
4
. (5)
Следовательно, при отсутствии тока через гальванометр с помощью пропорции (5) можно вы-
числить одно из сопротивлений моста, если известны остальные.
В лабораторной установке резисторы R
1
и R
2
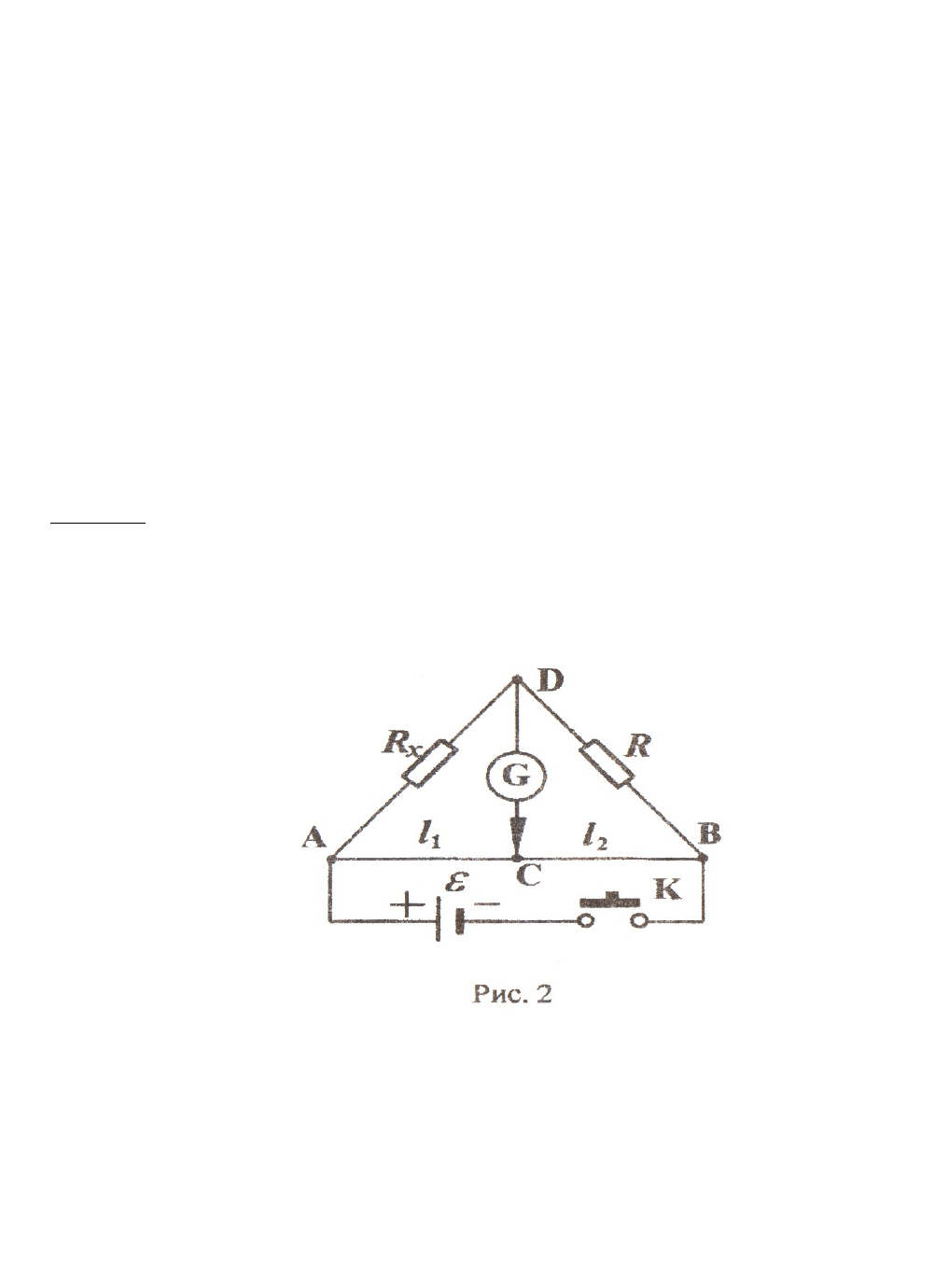
выполнены в виде реохорда - однородной метал-
лической проволоки сечения S c большим удельным сопротивление ρ, натянутой вдоль
миллиметровой шкалы (рис. 2). Соединение реохорда с гальванометром осуществляется через
скользящий контакт (движок) С. Таким образом, роль резисторов R
1
и R
2
играют отрезки проволоки с
длинами l
1
и l
2
, расположенные по разные стороны от движка. Перемещение движка позволяет
плавно изменять величины R
1
и R
2
. Их можно выразить следующим образом:
R
1
=(ρ/S)l
1
и R
2
=(ρ/S)l
2
, (6)
Подставляя выражение (6) в (5), получим рабочую формулу:
R
x
=(l
1
/l
2
)R. (7)
Она позволяет вычислить неизвестное сопротивление R
x
при известном R и равновесном для
моста соотношении l
1
/l
2
.
Задание. Измерение сопротивлений резисторов при их последовательном и параллельном
соединениях.
1. Собрать электрическую цепь по схеме (рис. 2), где R
x
= R
’
x
– первое из двух,
имеющихся в наборе, неизвестных сопротивлений R
’
x
и R
’’
x
, R- магазин
сопротивлений, К- ключ(кнопка).
2. Поставить в магазине произвольное сопротивление R, например, 1000 Ом.
Уравновесить мост, перемещая движок реохорда С до положения, при котором
стрелка гальванометра перестанет отклоняться при кратковременном замыкании
кнопки К. (Следует избегать длительного замыкания кнопки К, так как в этом случае
проводники будут нагреваться и, следовательно, изменять свое сопротивление).
3. Варьируя сопротивление магазина R, найти такое его значение, чтобы равновесие
моста достигалось для положения контакта С, находящегося вблизи средней части
реохорда.
4. Измерить длины плеч l1 и l2 уравновешенного моста. По формуле (7) вычислить
значение R
’
x
.

5. Определить R
’
x
при 5ти различных значениях сопротивления магазина. Следует
стремиться к тому, чтобы среди всех результатов отношение l1 к l2 больше и меньше
единицы встречалось одинаковое количество раз. Найти среднее значение R
’
x
.
6. Заменить резистор R
’
x
на R
’’
x
. Провести измерения сопротивления R
’’
x
по пунктам 2-5.
7. Измерить по пунктам 2-5 общее сопротивление резисторов R
’
x
и R
’’
x
при их
параллельном и последовательном соединениях.
8. Последние два результата измерений сопоставить с величинами, рассчитанными по
формулам для последовательного и параллельного соединения проводников: Rпос=
R
’
x
+R
’’
x
и Rпар= R
’
x
R
’’
x
/( R
’
x
+R
’’
x
).
Практика:
Резистор R
м
/Ом l
1
/см l
2
/см R
р
/Ом
R
’
x
180 23 28 147,9
93 29 22 122,6
75 32 19 126,3
199,5 20 31 128,7
260 17 34 130,0
R
’’
x
120 17 34 60,0
93 20 31 60,0
57 26 25 59,3
41 30 21 58,6
73 23 28 60,0
R
’
x
|| R
’’
x
49 22,7 28,3 39,3
39 25,6 25,4 39,3
29,9 27,4 23,6 34,7
26 30,7 20,3 39,3
62 20,3 30,7 41,0
106 14,2 36,8 40,9
R
’
x
послед. R
’’
x
230 23 28 188,9
380 17 34 190,0
290 20 31 187,1
179 26 25 186,2
130 30 21 185,7
Найдем среднее сопротивление резистров:
R
’
x
= 131,1 Ом
R
’’
x
= 59,6 Ом
R
||
= 39,1±1,6 Ом
R
пос
=187,6±2,5 Ом
Так же, рассчитаем по формулам для последовательного и параллельного соединения
проводников R
пос
= R
’
x
+ R
’’
x
и R
пар
= R
’
x
R
’’
x
/( R
’
x
+ R
’’
x
).
R
пос
=190,7 Ом
R
пар
=40,9 Ом

Вывод: Измерил электрическое сопротивление мостом Уитстона резисторов при их
последовательном и параллельном соединении, а также рассчитал их по формулам. Результаты
совпали в пределах погрешности эксперимента. Изучив мост Уитстона дал ему положительную
оценку как измерительному прибору.
