Итоговая контрольная работа по алгебре
Подождите немного. Документ загружается.


№ 1
1. Поле и основные свойства. (элементы отличная от нуля, частное)
2. Жорданова нормальная форма. (канонический вид, клетка)
3. Найти функцию Эйлера
?)375(
4. Является ли группой множества положительных действительных чисел с операциями
baba
5. Привести к каноническому виду
- матриц
200
120
012
)(
A
№ 2
1. Кольцо и основные свойства. (определение, распределенный закон сложения относительно умножения, единичный, обратные
элементы)
2. Унимодулярные
- матрицы. (эквивалентность, подобие матрицы, критерии эквивалентности)
3. Проверти теорему Эйлера а=5, m=24
4. является ли группой данное множество с данной операцией. (z,+)
5. Найти число делителей и сумму делителей от 375?
?)375(
,
?)375( s
№ 3
1. Группа и основные свойства. (единичный и обратные элементы, ассоциативность)
2. Эквивалентность
- матрицы. (элементные преобразования, канонический вид)
3. Найти остаток от деления 3
80
+7
80
на 11
4. Проверить подобие матриц:
321
1062
523
A
,
32204
51326
34206
B
5. Образует ли поле и кольцо с данным множеством относительно сложения и умножения:
),,( z
№ 4
1. Сравнения и их основные свойства. (деление составной, сравнение по модулю m, одинаковые остатки)
2. Жорданова нормальная форма. (подобные матрицы, нормальные формы, клетка Жордановой формы)
3. Решите сравнение по методу Эйлера:
)5(mod13 x
4. Привести к каноническому виду
- матриц:
2
)1(00
00
00)1(
)(
A
5. Найти остаток от деления 66
17
на 17?
№ 5
1. Мультипликативные функции
)(n
,
)(ns
и
)(n
. (число простых делителей, сумма простых делителей).
2. Группы и их основные свойства (аксиомы групп, единичный и обратный элемент, ассоциативность)
3. Определить последние две цифры числа 2
100
?
4. Найти Жорданова нормальную форму матриц:
221
041
040
A
5. Найти Эйлерову функцию числа 71?
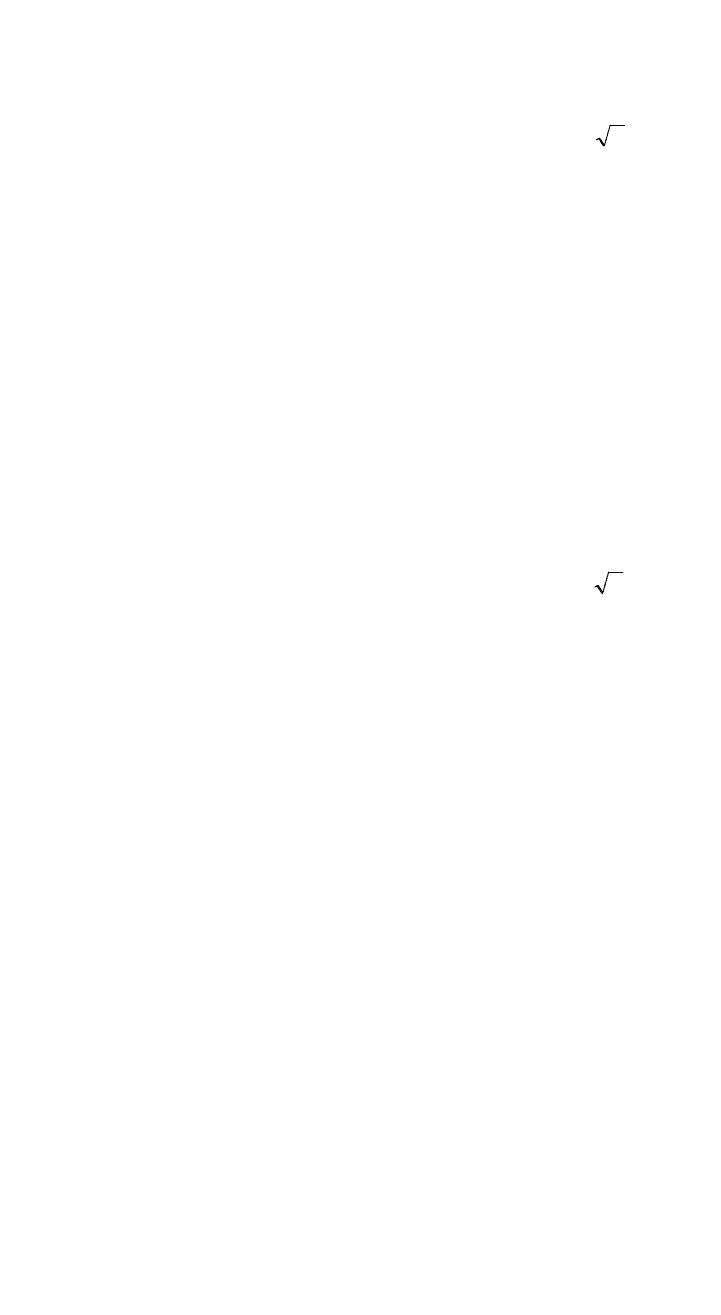
№ 6
1. Основные понятия об простых чисел. (определение, решетка Эратосфена)
2. Минимальный многочлен. Теорема Гамильтона-Кэли. (многочлен, минимальный многочлен, характеристический многочлен)
3. Если а разлагается на простые множители в виде
qpa
и
120)( a
, найти а?
4. Найти Жорданова нормальную форму матриц:
212
044
010
A
5. Образует ли данное множество относительно сложению и умножению кольцо и поле?
Zbaba ,|2
№ 7
1. Полная и приведенная система вычетов. Теоремы Эйлера и Ферма. (класс вычетов, абсолютно наименьшая)
2. Поле и основные свойства. (распределенный закон сложения относительно умножения, обратный элемент)
3. Является ли данное множество с данной операцией, группой
4. Найти функцию Эйлера
?)753(
5. Делиться ли на 1093
2
число 2
1093
-2?
№ 8
1. Мультипликативные функции
)(n
,
)(ns
и
)(n
. (число простых делителей, суммапростых делителей)
2. Унимодулярной
- матрицы. Подобие матриц. (
- матрица, канонический вид, подобные матрицы)
3. Проверьте теорему Эйлера для а=5, m=24.
4. Привести диагональному виду
0
1
)(A
5. Образует ли данная множества относительно сложению и умножению кольцо и поле?
Zbaba ,|7
№ 9
1. Основные определения простых чисел. (делители, решето Эратосфена)
2. Жорданова нормальная форма. (подобные матрицы, нормальная матрица, клетка)
3. Определите порядок элемента групп
21532
54321
4. Найти функцию Эйлера
?)498132(
5. Найти остаток от деления (12371
56
+ 38)
28
на 111
№ 10
1. Полная и приведенная система вычетов. (Сравнение по модулю m, по парно несравнимые, класс вычетов)
2. Минимальный многочлен Теорема Гамильтона-Кэли (многочлен, минимальный многочлен, характеристический матрица и
многочлен)
3. Ассоциативен или нет множество положительных действительных чисел относительно операции а*в=а:в?
4. Показать справедливости (а+в)
р
=а
р
+ в
р
(mod p), если р – простое.
5. Найти Жорданова нормальную форму матрицы:
544
446
235
A
№ 11
1. Эквивалентность
– матриц. (элементарная преобразование, λ- матрица, эквивалентность каноническому виду)
2. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
3. Найти остаток от деления: 3
100
+ 5
100
на 7
4. Проверьте подобие матриц:
221
551
1566
A
1170119
41734
42037
B
5. Образуют ли кольцо и поле данное множество относительно сложения и деления: (2Z,+)
№ 12
1. Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)

2. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный, обратные
элементы)
3. Проверь теорему Эйлера для а=3, m=16?
4. Образуют ли группу данная множество относительно сложения и умножения: (R,+)
5. Найти
?)720(
и
?)720( S
№ 13
1. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный, обратные
элементы)
2. Минимальный многочлен Теорема Гамильтона-Кэли (многочлен, минимальный многочлен, характеристический матрица и
многочлен)
3. Составит сравнение пользуясь теорему Эйлера по п=8
4. Образуют ли группу множество действительных чисел относительно операции
22
вава
5. Разложите на простые множители число
1818
32
№ 14
1.Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)
2. Жорданова нормальная форма. (подобные матрицы, нормальная матрица, клетка)
3.Покажите что числа 23,19,-19,25 образует приведенная система вычетов по моделу п=12
4.Найти все простые числи между 2320 и 2350.
5. Проверьте теорему Эйлера для а=3, m=16.
№ 15
1. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
2. Некоторые применение теория чисел(единичный элемент, обратная элемент, ассосативност)
3. Покажите делимость числа
)(
5
Пттт
на 30.
4. Образуют ли кольцо и поле множество : (
Qвава ,7
) .
5. Найти а если
22
11424)( qриаа
где р и q простые множители.
№ 16
1. Поле и основные свойства. (элементы отличная от нуля, частное)
2. .Жорданова нормальная форма. (канонический вид, клетка)
3. Найти функцию Эйлера
?)375(
4. Является ли группой множества положительных действительных чисел с операциями
baba
5. Привести к каноническому виду
- матриц
200
120
012
)(
A
№ 17
1. Кольцо и основные свойства. (определение, распределенный закон сложения относительно умножения, единичный,
обратные элементы)
2. Унимодулярные
- матрицы. (эквивалентность, подобие матрицы, критерии эквивалентности)
3. Проверти теорему Эйлера а=5, m=24
4. является ли группой данное множество с данной операцией. (z,+)
5. Найти число делителей и сумму делителей от 375?
?)375(
,
?)375( s
№18
1. Группа и основные свойства. (единичный и обратные элементы, ассоциативность)
2. Эквивалентность
- матрицы. (элементные преобразования, канонический вид)
3. Найти остаток от деления 3
80
+7
80
на 11
4. Проверить подобие матриц:
321
1062
523
A
,
32204
51326
34206
B
5. Образует ли поле и кольцо с данным множеством относительно сложения и умножения:
),,( z
№ 19
1. Сравнения и их основные свойства. (деление составной, сравнение по модулю m, одинаковые остатки)
2. Жорданова нормальная форма. (подобные матрицы, нормальные формы, клетка Жордановой формы)
3. Решите сравнение по методу Эйлера:
)5(mod13 x
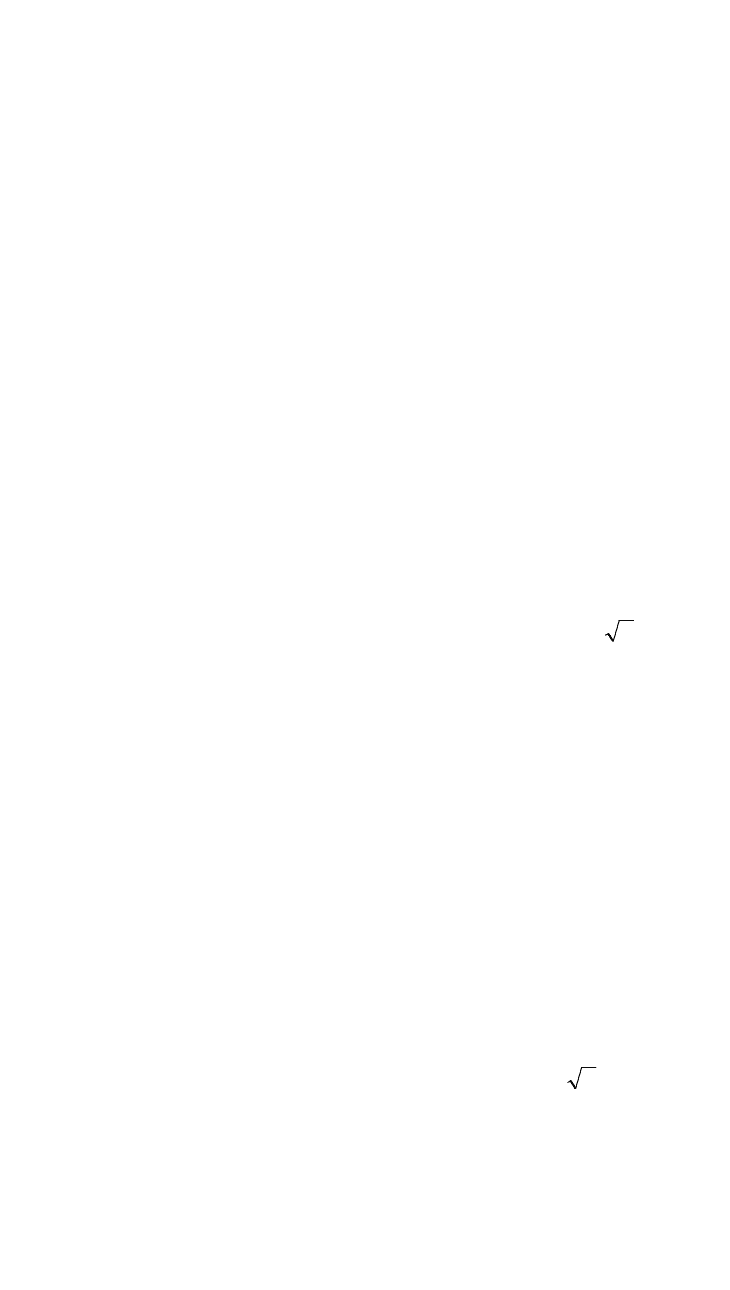
4. Привести к каноническому виду
- матриц:
2
)1(00
00
00)1(
)(
A
5. Найти остаток от деления 66
17
на 17?
№ 20
1. Мультипликативные функции
)(n
,
)(ns
и
)(n
. (число простых делителей, сумма простых делителей).
2. Группы и их основные свойства (аксиомы групп, единичный и обратный элемент, ассоциативность)
3. Определить последние две цифры числа 2
100
?
4. Найти Жорданова нормальную форму матриц:
221
041
040
A
5. Найти Эйлерову функцию числа 71?
№ 21
1. Основные понятия об простых чисел. (определение, решетка Эратосфена)
2. Минимальный многочлен. Теорема Гамильтона-Кэли. (многочлен, минимальный многочлен, характеристический
многочлен)
3. Если а разлагается на простые множители в виде
qpa
и
120)( a
, найти а?
4. Найти Жорданова нормальную форму матриц:
212
044
010
A
5. Образует ли данное множество относительно сложению и умножению кольцо и поле?
Zbaba ,|2
№ 22
1. Полная и приведенная система вычетов. Теоремы Эйлера и Ферма. (класс вычетов, абсолютно наименьшая)
2. Поле и основные свойства. (распределенный закон сложения относительно умножения, обратный элемент)
3. Является ли данное множество с данной операцией, группой
4. Найти функцию Эйлера
?)753(
5. Делиться ли на 1093
2
число 2
1093
-2?
№ 23
1. Мультипликативные функции
)(n
,
)(ns
и
)(n
. (число простых делителей, суммапростых делителей)
2. Унимодулярной
- матрицы. Подобие матриц. (
- матрица, канонический вид, подобные матрицы)
3. Проверьте теорему Эйлера для а=5, m=24.
4. Привести диагональному виду
0
1
)(A
5. Образует ли данная множества относительно сложению и умножению кольцо и поле?
Zbaba ,|7
№ 24
1. Основные определения простых чисел. (делители, решето Эратосфена)
2. Жорданова нормальная форма. (подобные матрицы, нормальная матрица, клетка)
3. Определите порядок элемента групп
21532
54321
4. Найти функцию Эйлера
?)498132(
5. Найти остаток от деления (12371
56
+ 38)
28
на 111
№ 25
1. Полная и приведенная система вычетов. (Сравнение по модулю m, по парно несравнимые, класс вычетов)
2. Минимальный многочлен Теорема Гамильтона-Кэли (многочлен, минимальный многочлен, характеристический матрица и
многочлен)
3. Ассоциативен или нет множество положительных действительных чисел относительно операции а*в=а:в?
4. Показать справедливости (а+в)
р
=а
р
+ в
р
(mod p), если р – простое.

5. Найти Жорданова нормальную форму матрицы:
544
446
235
A
№ 26
1. Эквивалентность
– матриц. (элементарная преобразование, λ- матрица, эквивалентность каноническому виду)
2. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
3. Найти остаток от деления: 3
100
+ 5
100
на 7
4. Проверьте подобие матриц:
221
551
1566
A
1170119
41734
42037
B
5. Образуют ли кольцо и поле данное множество относительно сложения и деления: (2Z,+)
№ 27
1. Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)
2. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный,
обратные элементы)
3. Проверь теорему Эйлера для а=3, m=16?
4. Образуют ли группу данная множество относительно сложения и умножения: (R,+)
5. Найти
?)720(
и
?)720( S
№ 28
1. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный,
обратные элементы)
2. Минимальный многочлен Теорема Гамильтона-Кэли (многочлен, минимальный многочлен, характеристический матрица и
многочлен)
3. Составит сравнение пользуясь теорему Эйлера по п=8
4. Образуют ли группу множество действительных чисел относительно операции
22
вава
5. Разложите на простые множители число
1818
32
№ 29
1.Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)
2. Жорданова нормальная форма. (подобные матрицы, нормальная матрица, клетка)
3.Покажите что числа 23,19,-19,25 образует приведенная система вычетов по модулу п=12
4.Найти все простые числи между 2320 и 2350.
5. Проверьте теорему Эйлера для а=3, m=16.
№ 30
1. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
2. Некоторые применение теория чисел(единичный элемент, обратная элемент ,ассосативност)
3. Покажите делимость числа
)(
5
Пттт
на 30.
4. Образуют ли кольцо и поле множество : (
Qвава ,7
) .
5. Найти а если
22
11424)( qриаа
где р и q простые множители.
№ 31
1. Эквивалентность
– матриц. (элементарная преобразование, λ- матрица, эквивалентность каноническому виду)
2. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
3. Найти остаток от деления: 3
100
+ 5
100
на 7
4. Проверьте подобие матриц:
221
551
1566
A
1170119
41734
42037
B
5. Образуют ли кольцо и поле данное множество относительно сложения и деления: (2Z,+)
№ 32
1. Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)
2. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный,
обратные элементы)
3. Проверь теорему Эйлера для а=3, m=16?
4. Образуют ли группу данная множество относительно сложения и умножения: (R,+)
5. Найти
?)720(
и
?)720( S
№ 33
1. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный,
обратные элементы)

2. Минимальный многочлен Теорема Гамильтона-Кэли (многочлен, минимальный многочлен, характеристический матрица и
многочлен)
3. Составит сравнение пользуясь теорему Эйлера по п=8
4. Образуют ли группу множество действительных чисел относительно операции
22
вава
5. Разложите на простые множители число
1818
32
№ 34
1.Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)
2. Жорданова нормальная форма. (подобные матрицы, нормальная матрица, клетка)
3.Покажите что числа 23,19,-19,25 образует приведенная система вычетов по моделу п=12
4.Найти все простые числи между 2320 и 2350.
5. Проверьте теорему Эйлера для а=3, m=16.
№ 35
1. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
2. Некоторые применение теория чисел(единичный элемент, обратная элемент, ассосативност)
3. Покажите делимость числа
)(
5
Пттт
на 30.
4. Образуют ли кольцо и поле множество : (
Qвава ,7
) .
5. Найти а если
22
11424)( qриаа
где р и q простые множители.
№ 36
1. Поле и основные свойства. (элементы отличная от нуля, частное)
2. Жорданова нормальная форма. (канонический вид, клетка)
3. Найти функцию Эйлера
?)375(
4. Является ли группой множества положительных действительных чисел с операциями
baba
5. Привести к каноническому виду
- матриц
200
120
012
)(
A
№ 37
1. Кольцо и основные свойства. (определение, распределенный закон сложения относительно умножения, единичный,
обратные элементы)
2. Унимодулярные
- матрицы. (эквивалентность, подобие матрицы, критерии эквивалентности)
3. Проверти теорему Эйлера а=5, m=24
4. является ли группой данное множество с данной операцией. (z,+)
5. Найти число делителей и сумму делителей от 375?
?)375(
,
?)375( s
№38
1. Группа и основные свойства. (единичный и обратные элементы, ассоциативность)
2. Эквивалентность
- матрицы. (элементные преобразования, канонический вид)
3. Найти остаток от деления 3
80
+7
80
на 11
4. Проверить подобие матриц:
321
1062
523
A
,
32204
51326
34206
B
5. Образует ли поле и кольцо с данным множеством относительно сложения и умножения:
),,( z
№ 39
1. Сравнения и их основные свойства. (деление составной, сравнение по модулю m, одинаковые остатки)
2. Жорданова нормальная форма. (подобные матрицы, нормальные формы, клетка Жордановой формы)
3. Решите сравнение по методу Эйлера:
)5(mod13 x
4. Привести к каноническому виду
- матриц:
2
)1(00
00
00)1(
)(
A
5. Найти остаток от деления 66
17
на 17?
№ 40
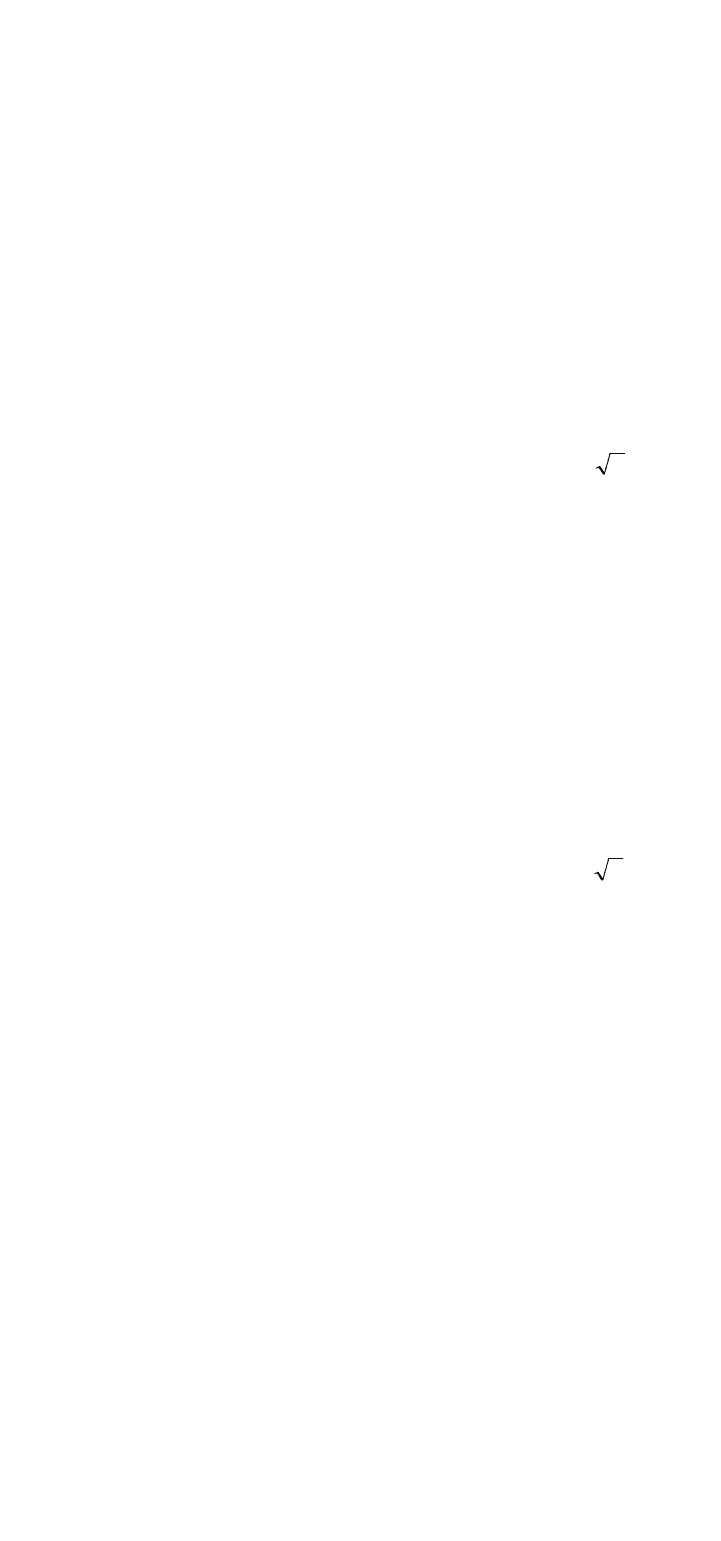
1. Мультипликативные функции
)(n
,
)(ns
и
)(n
. (число простых делителей, сумма простых делителей).
2. Группы и их основные свойства (аксиомы групп, единичный и обратный элемент, ассоциативность)
3. Определить последние две цифры числа 2
100
?
4. Найти Жорданова нормальную форму матриц:
221
041
040
A
5. Найти Эйлерову функцию числа 71?
№ 41
1. Основные понятия об простых чисел. (определение, решетка Эратосфена)
2. Минимальный многочлен. Теорема Гамильтона-Кэли. (многочлен, минимальный многочлен, характеристический
многочлен)
3. Если а разлагается на простые множители в виде
qpa
и
120)( a
, найти а?
4. Найти Жорданова нормальную форму матриц:
212
044
010
A
5. Образует ли данное множество относительно сложению и умножению кольцо и поле?
Zbaba ,|2
№ 42
1. Полная и приведенная система вычетов. Теоремы Эйлера и Ферма. (класс вычетов, абсолютно наименьшая)
2. Поле и основные свойства. (распределенный закон сложения относительно умножения, обратный элемент)
3. Является ли данное множество с данной операцией, группой
4. Найти функцию Эйлера
?)753(
5. Делиться ли на 1093
2
число 2
1093
-2?
№ 43
1. Мультипликативные функции
)(n
,
)(ns
и
)(n
. (число простых делителей, суммапростых делителей)
2. Унимодулярной
- матрицы. Подобие матриц. (
- матрица, канонический вид, подобные матрицы)
3. Проверьте теорему Эйлера для а=5, m=24.
4. Привести диагональному виду
0
1
)(A
5. Образует ли данная множества относительно сложению и умножению кольцо и поле?
Zbaba ,|7
№ 44
1. Основные определения простых чисел. (делители, решето Эратосфена)
2. Жорданова нормальная форма. (подобные матрицы, нормальная матрица, клетка)
3. Определите порядок элемента групп
21532
54321
4. Найти функцию Эйлера
?)498132(
5. Найти остаток от деления (12371
56
+ 38)
28
на 111
№ 45
1. Полная и приведенная система вычетов. (Сравнение по модулю m, по парно несравнимые, класс вычетов)
2. Минимальный многочлен Теорема Гамильтона-Кэли (многочлен, минимальный многочлен, характеристический матрица и
многочлен)
3. Ассоциативен или нет множество положительных действительных чисел относительно операции а*в=а:в?
4. Показать справедливости (а+в)
р
=а
р
+ в
р
(mod p), если р – простое.
5. Найти Жорданова нормальную форму матрицы:
544
446
235
A
№ 46
1. Эквивалентность
– матриц. (элементарная преобразование, λ- матрица, эквивалентность каноническому виду)
2. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
3. Найти остаток от деления: 3
100
+ 5
100
на 7
4. Проверьте подобие матриц:
221
551
1566
A
1170119
41734
42037
B
5. Образуют ли кольцо и поле данное множество относительно сложения и деления: (2Z,+)

№ 47
1. Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)
2. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный,
обратные элементы)
3. Проверь теорему Эйлера для а=3, m=16?
4. Образуют ли группу данная множество относительно сложения и умножения: (R,+)
5. Найти
?)720(
и
?)720( S
№ 48
1. Кольцо и основные свойства. (определения, распределенный закон сложения относительно умножения, единичный,
обратные элементы)
2. Минимальный многочлен Теорема Гамильтона-Кэли (многочлен, минимальный многочлен, характеристический матрица и
многочлен)
3. Составит сравнение пользуясь теорему Эйлера по п=8
4. Образуют ли группу множество действительных чисел относительно операции
22
вава
5. Разложите на простые множители число
1818
32
№ 49
1.Сравнение и их основные свойства. (деление с остатком, сравнения по модулю m, одинаковые остатки)
2. Жорданова нормальная форма. (подобные матрицы, нормальная матрица, клетка)
3.Покажите что числа 23,19,-19,25 образует приведенная система вычетов по модему п=12
4.Найти все простые числи между 2320 и 2350.
5. Проверьте теорему Эйлера для а=3, m=16.
№ 50
1. Группы и их основные свойства. (определение аксиомы сложения и умножения, единичный, обратные элементы)
2. Некоторые применение теория чисел (единичный элемент, обратная элемент, ассосативност )
3. Покажите делимость числа
)(
5
Пттт
на 30.
4. Образуют ли кольцо и поле множество : (
Qвава ,7
) .
5. Найти а если
22
11424)( qриаа
где р и q простые множители.
