Ильин А.П., Гордина Н.Е. Химия твердого тела

Подождите немного. Документ загружается.

Таблица 2.2

14 решеток Браве

Тип решетки

Сингония

примитив-

ная

базо-

центрирован-

ная

объемно-

центрирован-

ная

гране-

центрирован-

ная

Триклинная

Моноклинная

Ромбическая

Тригональная

(ромбоэдриче-

ская)

Тетрагональная

Гексагональная

Кубическая

2.3. Элементы симметрии кристаллических структур

Понятие класса (вида) симметрии кристалла эквивалентно понятию то-

чечной группы симметрии. Понятие группы дается в математике (теория

группы) следующим образом. Множество различных элементов а, в, с… со-

ставляют математическую группу, если оно удовлетворяет следующим усло-

виям:

• произведение любых двух элементов или квадрат какого-либо эле-

мента множества принадлежит тому же множеству;

• для любых трех элементов множества выполняется ассоциативный

(сочетательный) закон

саввса )()(

;

• в множестве существует единичный (нейтральный) элемент е такой,

что

еа

ае

;

• для любого элемента а существует элемент а

-1

, принадлежащий тому

же множеству, так что

саааа ==

−− 11

Всем этим условиям удовлетворяет любой из 32 видов симметрии.

Симметрия кристаллов (конечных фигур) может быть охарактеризова-

на с помощью следующих элементов симметрии: С, L

, L

, P,

которые в литературе иногда называют закрытыми элементами симметрии,

поскольку они могут быть применены к ограниченному участку пространст-

ва. Однако внутренняя симметрия кристалла гораздо сложнее внешней.

Основные свойства кристаллической структуры и характеризующей ее

пространственной решетки – бесконечная периодичность: любые два узла

решетки можно совместить друг с другом при помощи трансляции. Трансля-

ция является самым характерным элементом симметрии бесконечных фигур.

Трансляция – бесконечно повторяющийся параллельный перенос на

некоторое определенное расстояние, называемое периодом трансляции.

Сочетание трансляций с плоскостями и осями симметрии дает еще два

новых элемента симметрии: плоскости скользящего отражения и винтовые

оси симметрии. Винтовые оси симметрии и плоскости скользящего отраже-

ния называют иногда открытыми элементами симметрии.

2.4. Понятия пространственной группы симметрии

Все возможные сочетания элементов симметрии 32 точечных групп и

14 решеток Бравэ приводят к появлению 230 пространственных групп сим-

метрии. Е.С.Федоров впервые в 1890 г. доказал, что 32 точечным группам

соответствует 230 пространственных групп симметрии. Структура любого

кристаллического вещества относится к одной из этих пространственных

групп. Каждой точечной группе соответствует несколько пространственных

групп. Пространственной группой симметрии называется совокупность всех

возможных элементов симметрии кристаллической структуры.

Пространственная группа симметрии характеризует симметрию струк-

туры кристалла, так же как точечная группа симметрии характеризует сим-

метрию внешней формы кристалла и его физические свойства.

Для обозначения пространственных групп применяются символы, со-

держащие от 2 до 4 позиций. В первой позиции всегда записывается заглав-

ная буква, обозначающая тип решетки: Р – примитивная, F – гранецентриро-

ванная, I – объемно-центрированная, А, В, С – базоцентрированная соответ-

ствующей ориентации. Остальные позиции отвечают некоторым имеющимся

элементам симметрии.

Например: Рт3т – структура перовскита CaTiO

Fт3т – структура NaCl.

Пространственная группа характеризуется не только набором элемен-

тов симметрии, но и числом симметрично эквивалентных позиций (правиль-

ной системой точек).

Правильной системой точек называется совокупность симметрично эк-

вивалентных позиций (точек), связанных между собой симметричными пре-

образованиями пространственной группы. Правильную систему точек можно

получить при помощи всех операций симметрии, свойственных данной про-

странственной группе.

Понятие правильной системы точек для пространственной группы иг-

рает такую же роль, как и понятие простой формы для точечной группы.

Знание правильной системы точек необходимо для того, чтобы установить

число атомов разного типа, которые можно разместить в элементарной ячей-

ке.

2.5. Примеры открытых элементов симметрии

Сочетание трансляции с плоскостями и осями симметрии дает еще два

новых элемента симметрии: плоскости скользящего отражения и винтовые

оси симметрии, которые называют открытыми элементами симметрии.

Международные обозначения элементов симметрии структур показаны на

рис.2.3.

Оси

Вертикальные Горизонтальные Наклонные

Плоскости

Вертикальные Горизонтальные Наклонные

Рис.2.3. Международные обозначения элементов симметрии

Различают три плоскости отражения - а, в, с, действующие соответст-

венно переносу вдоль первой x, второй y или третьей z оси. Величина посту-

пления здесь равна половине трансляции. Плоскость скользящего отражения

включает в себя два совместных действия: плоскости симметрии и парал-

лельной ей трансляции.

Кроме того, имеются еще плоскости скользящего отражения n и d.

Компоненты скольжения плоскостей n и d направлены по диагоналям сторон

элементарной ячейки и, соответственно, равны их половинам и четвертям.

Для n поступления они равны 1/2 (в+с), 1/2 (с+а), 1/2 (a+в) для d - 1/4(в+с),

1/4(с+а), 1/4(а+в).

Действие плоскости d ограничено случаями гранецентрированных

трансляционных решеток.

Плоскости а, в, с легко обнаруживаются на моделях структур типа

NaCl (рис.2.4).

а б

Рис. 2.4. Плоскости скользящего отражения а и b на узоре шахматной

доски (а) и на сетке куба (б) элементарной ячейки NaCl

Для практического освоения плоскостей скользящего отражения n и d

следует рассмотреть пространственные модели кристаллических структур

(n– на структуре

−

Fe– объемно-центрированная кубическая решетка

(рис.2.5) и d – на структуре алмаза – гранецентрированная кубическая ре-

шетка).

а б

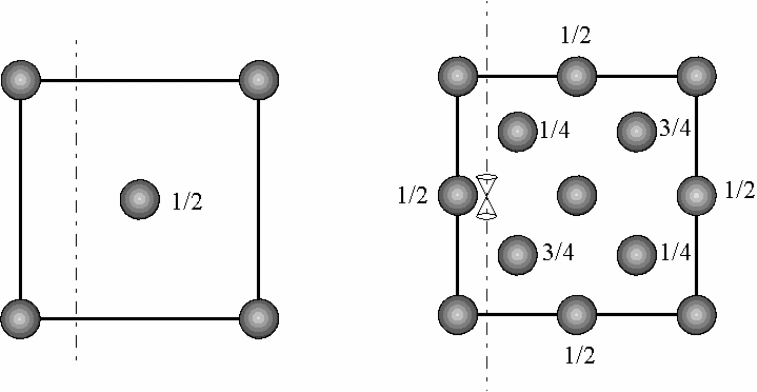
Рис. 2.5. Плоскости скользящего отражения в структуре α-Fe (a) и ал-

маза (б)

Если атомы (рис.2.5, а) по вершинам ячейки находятся в плоскости

чертежа, то атом в центре находится над плоскостью чертежа на расстоянии

с/2, т.е. на 1/2 трансляции вдоль оси z. Это обозначено на чертеже цифрой

1/2. Атом Fe можно совместить с атомом Fe в центре, если осуществить од-

новременно отражение в плоскости n и скольжение в этой плоскости на а/2, а

затем с/2.Записывается (а+с)/2. Можно провести аналогичную операцию

(в+с)/2.

Плоскости скользящего отражения типа d, или «алмазные», характерны

только для гранецентрированных решеток. Они присутствуют в структуре

алмаза (рис.2.5, б).

Компоненты скольжения направлены вдоль плоскостей диагонали эле-

ментарного параллелограмма, расположенного в плоскости отражения, а ве-

личина переноса составляет 1/4 длины диагонали: (а+в)/4, (а+с)/4, (в+с)/4.

Элементарная ячейка структуры алмаза гранецентрированная кубиче-

ская, внутри ее есть еще четыре атома. Эти атомы размещены в центрах 4-х

октантов. Еще 4 октанта (центры) не заняты атомами – два на высоте 1/4 и

два – на высоте 3/4. Высоты 1/4 и 3/4 измеряются в долях параметра ячейки

по оси С.

Условное обозначение плоскостей скользящего отражения a, b, c, n, d

показано на рисунке 2.5.

Винтовой осью симметрии называется совокупность оси симметрии и

параллельного ей переноса, действующих совместно (рис.2.6). Винтовые оси

могут быть второго, третьего, четвертого и шестого порядка (или двойные,

тройные, четверные, шестерные).

Порядок оси n равен:

360

, где

– минимальный угол поворота в операции симметрии.

Различают правые и левые винтовые оси. В случае правой винтовой

оси перемещение вдоль оси сопряжено с вращением по часовой стрелке, а в

случае левой – против часовой стрелки.

Действие двойной винтовой оси равно повороту на 180

с последую-

щим поступанием вдоль нее. Величина последнего равна половине элемен-

тарной трансляции вдоль оси. Отсюда понятно обозначение этой оси - 2

ПТа

ПТ=а/2

31 434241

Рис. 2.6. Винтовые оси симметрии второго, третьего и четвертого

порядков.

Двойная винтовая ось является одновременно и правой и левой, так

как повороты вокруг нее на 180

и вправо и влево приводят к тождественно-

му результату.

При описании структур кристаллов винтовые оси обозначаются сле-

дующим образом: 2

, 3

, 4

, 6

. В этих обозначениях ча-

стное от деления маленькой цифры на большую, впереди стоящую, дает ве-

личину поступания t вдоль оси по отношению к элементарной трансляции

структуры Т в направлении, параллельном данной оси.

На рисунке 2.7 изображены тройные оси: простая поворотная 3 и две

винтовые – правая 3

и левая 3

. Действие правой тройной винтовой оси со-

стоит в повороте точек на 120

по часовой стрелке с последующим поступа-

нием их вдоль оси на одну треть элементарной трансляции. В случае левой

винтовой оси поворот на 120

производится против часовой стрелки.

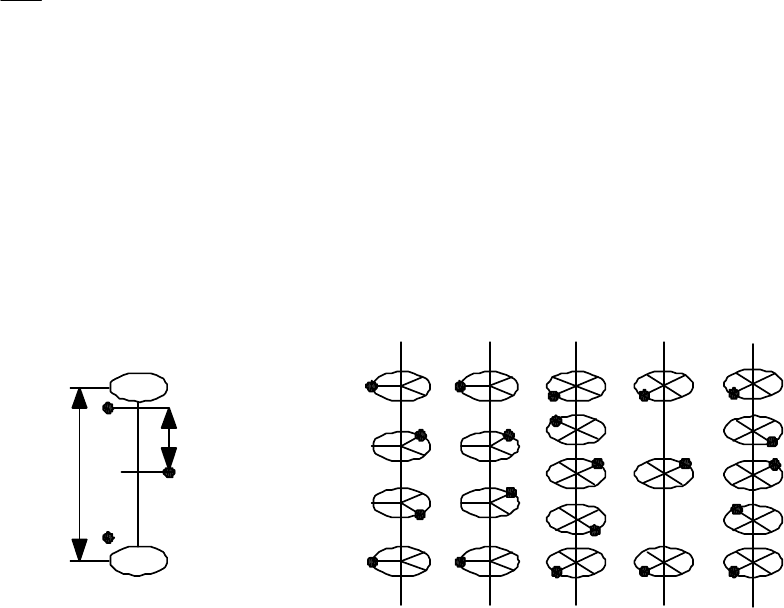
Рис. 2.7. Тройная

поворотная ось симметрии

(а), тройные винтовые оси

– правая 3

(б) и левая 3

(в)

Обозначение 3

вы-

ясняется с помощью ри-

сунка 2.7, а и 2.7, в. Как

видно из данных рисунков, в случае правой винтовой оси точка 2 перемеще-

на вверх на одну треть трансляции. В случае левой оси точка 3, лежащая на

аналогичном ребре изображенной тригональной призмы, поднята на 2/3 та-

кой трансляции.

На рисунке 2.8, помимо простой четверной поворотной оси симметрии

4, изображены четверные винтовые оси – правая 4

, левая 4

и нейтральная,

являющаяся одновременно простой двойной осью 4

. Поступание для по-

следней оси равно половине, а не четверти элементарной трансляции. Для

практического ознакомления с этими осями рекомендуем студентам рас-

смотреть пространственные модели кристаллических структур. Оси 4 и 4

легко обнаружить на структуре NaCl, оси 4

и 4

– на структурах алмаза и

циркона Zr(SiO

Рис. 2.8. Чет-

верная поворотная

ось симметрии 4 (а) и

четверные винтовые

оси – правая 4

(б),

нейтральная 4

(в) и

левая 4

(г)

На рисунке 2.9 изображены шестерные оси: простая поворотная 6 и

винтовые - 6

и левая 6

Рис. 2.9. Шестерная поворотная ось симметрии 6 (а) и шестерные вин-

товые оси – правые 6

и 6

(б и в), нейтральная 6

(г) и левые 6

и 6

(д и е)

Кроме того, существуют правая и левая шестерные винтовые оси 6

с поступаниями на одну треть элементарной трансляции, являющиеся од-

новременно двойными поворотными осями симметрии. Наконец, имеем ней-

тральную шестерную винтовую ось 6

с поступанием на половину элемен-

тарной трансляции, совпадающую с тройной поворотной осью.

Расположение винтовых осей в структурах алмаза и магния показано

на рис.2.10.

а б

Рис. 2.10. Элементарные ячейки структур, с указанием расположения

винтовых осей: а– алмаза; б– магния

2.6. Основные понятия в кристаллохимии

Описание кристаллохимических ячеек

Число атомов в элементарной ячейке

Чтобы правильно понимать структуру кристалла, необходимо научить-

ся подсчитывать на модели или по рисунку число атомов каждого химиче-

ского элемента, приходящихся на одну элементарную ячейку. Атомы, обра-

зующие ячейку, принадлежат ей только на определенную часть. Так, для всех

ячеек, кроме гексагональной, атом в вершине принадлежит ей только на 1/8

часть. Атом на грани ячейки принадлежит последней на 1/2, на ребре на 1/4

часть (табл.2.3, рис.2.11, 2.12).

1/2

1/4 3/4

3/4

1/4

1/2

1/4

3/4